前端也要懂物理 —— 慣性滾動篇
- 2020 年 6 月 11 日
- 筆記
- CSS3, javascript

作者:凹凸曼-吖偉
我們在平時編程開發時,除了需要關注技術實現、演算法、程式碼效率等因素之外,更要把所學到的學科知識(如物理學、理論數學等等)靈活應用,畢竟理論和實踐相輔相成、密不可分,這無論是對於我們的方案選型、還是技術實踐理解都有非常大的幫助。今天就讓我們一起來回顧中學物理知識,並靈活運用到慣性滾動的動效實現當中。
慣性滾動(也叫 滾動回彈,momentum-based scrolling)最早是出現在 iOS 系統中,是指 當用戶在終端上滑動頁面然後把手指挪開,頁面不會馬上停下而是繼續保持一定時間的滾動效果,並且滾動的速度和持續時間是與滑動手勢的強烈程度成正比。抽象地理解,就像高速行駛的列車制動後依然會往前行駛一段距離才會最終停下。而且在 iOS 系統中,當頁面滾動到頂/底部時,還有可能觸發 「回彈」 的效果。這裡錄製了微信 APP 【賬單】頁面中的 iOS 原生時間選擇器的慣性滾動效果:

熟悉 CSS 開發的同學或許會知道,在 Safari 瀏覽器中有這樣一條 CSS 規則:
-webkit-overflow-scrolling: touch;
當其樣式值為 touch 時,瀏覽器會使用具有回彈效果的滾動, 即「當手指從觸控螢幕上移開,內容會繼續保持一段時間的滾動效果」。除此之外,在豐富多姿的 web 前端生態中,很多經典組件的交互都一定程度地沿用了慣性滾動的效果,譬如下面提到的幾個流行 H5 組件庫中的例子。
流行 UI 庫效果
為了方便對比,我們先來看看一個 H5 普通長列表在 iOS 系統下(開啟了滾動回彈)的滾動表現:

-
weui 的 picker 組件
明顯可見,weui 選擇器的慣性滾動效果非常弱,基本上手從螢幕上移開後滾動就很快停止了,體驗較為不好。
-
vant 的 picker 組件
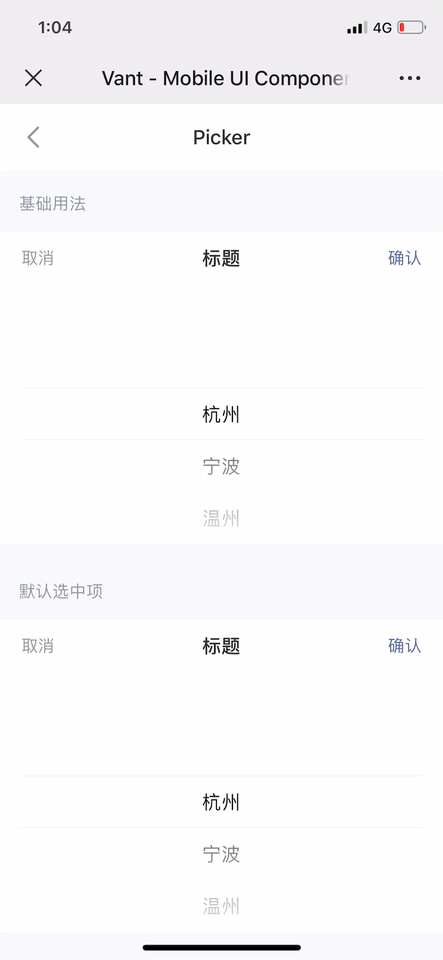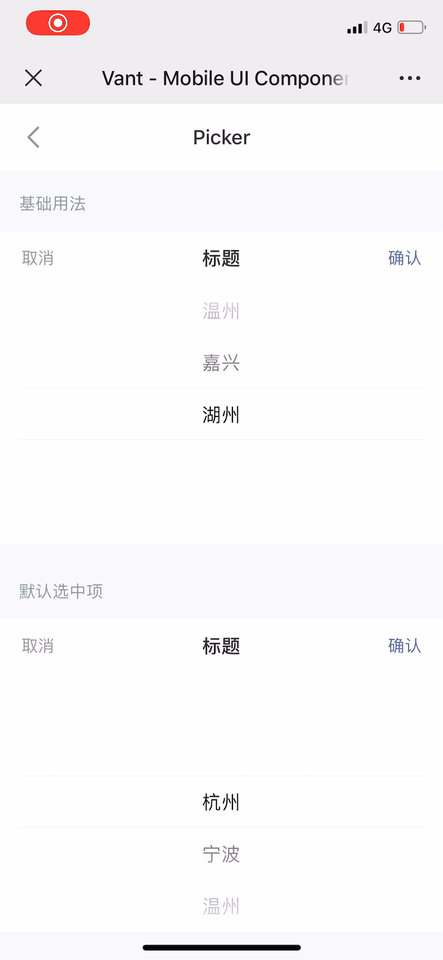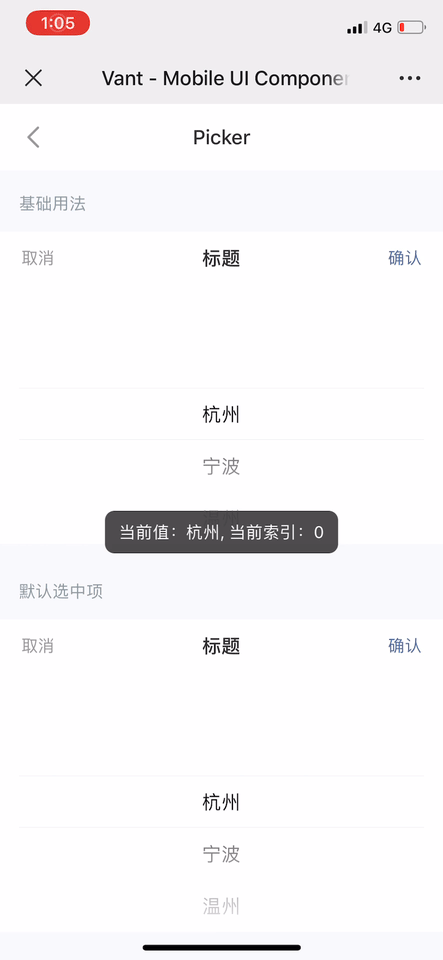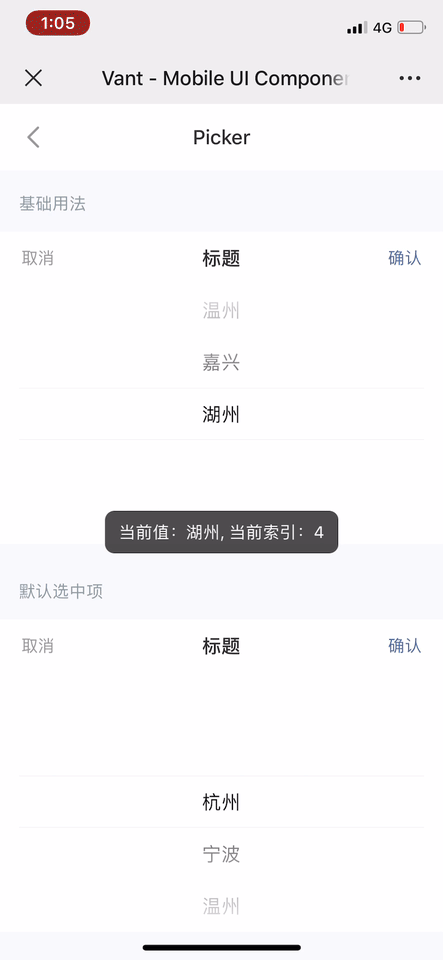
相比之下,vant 選擇器的慣性滾動效果則明顯清晰得多,但是由於觸頂/底回彈時依然維持了普通滾動時的係數或持續時間,導致整體來說回彈的效果有點脫節。
應用物理學模型
慣性 一詞來源於物理學中的慣性定律(即 牛頓第一定律):一切物體在沒有受到力的作用的時候,運動狀態不會發生改變,物體所擁有的這種性質就被稱為慣性。可想而知,慣性滾動的本質就是物理學中的慣性現象,因此,我們可以恰當利用中學物理上的 滑塊模型 來描述慣性滾動全過程。
為了方便描述,我們把瀏覽器慣性滾動效果中的滾動目標(如瀏覽器中的頁面元素)模擬成滑塊模型中的 滑塊。而且分析得出,慣性滾動的全過程可以模擬為(人)使滑塊滑動一定距離然後釋放的過程,那麼,全流程可以拆解為以下兩個階段:
-
第一階段,滑動滑塊使其從靜止開始做加速運動;

在此階段,滑塊受到的
F拉大於F摩使其從左到右勻加速前進。需要注意的是,對於瀏覽器的慣性滾動來說,我們一般關注的是用戶即將釋放手指前的一小階段,而非滾動的全流程(全流程意義不大),這一瞬間階段可以簡單模擬為滑塊均衡受力做 勻加速運動。
-
第二階段,釋放滑塊使其在只受摩擦力的作用下繼續滑動,直至最終靜止;
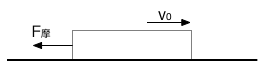
在此階段,滑塊只受到反向的摩擦力,會維持從左到右的運動方向減速前進然後停下。
基於滑塊模型,我們需要找到適合的量化指標來建立慣性滾動的計算體系。結合模型和具體實現,我們需要關注 滾動距離、速度曲線 以及 滾動時長 這幾個關鍵指標,下面會一一展開解析。
滾動距離
對於滑動模型的第一階段,滑塊做勻加速運動,我們不妨設滑塊的滑動距離為 s1,滑動的時間為 t1,結束時的臨界點速度(末速度)為 v1 ,根據位移公式

可以得出速度關係

對於第二階段,滑塊受摩擦力 F拉 做勻減速運動,我們不妨設滑動距離為 s2,滑動的時間為 t2,滑動加速度為 a,另外初速度為 v1,末速度為 0m/s,結合位移公式和加速度公式

可以推算出滑動距離 s2

由於勻減速運動的加速度為負(即 a < 0),不妨設一個加速度常量 A,使其滿足 A = -2a 的關係,那麼滑動距離

然而在瀏覽器實際應用時,v1 算平方會導致最終計算出的慣性滾動距離太大(即對滾動手勢的強度感應過於靈敏),我們不妨把平方運算去掉:

所以,求慣性滾動的距離(即 s2)時,我們只需要記錄用戶滾動的 距離 s1 和 滾動時長 t1,並設置一個合適的 加速度常量 A 即可。
經大量測試得出,加速度常量
A的合適值為0.003。
另外,需要注意的是,對於真正的瀏覽器慣性滾動效果來說,這裡討論的滾動距離和時長是指能夠作用於慣性滾動的範圍內的距離和時長,而非用戶滾動頁面元素的全流程,詳細的可以看【啟停條件】這一節內容。
慣性滾動速度曲線
針對慣性滾動階段,也就是第二階段中的勻減速運動,根據位移公式可以得到位移差和時間間距 T 的關係

不難得出,在同等時間間距條件下,相鄰兩段位移差會越來越小,換句話說就是慣性滾動的偏移量增加速度會越來越小。這與 CSS3 transition-timing-function 中的 ease-out 速度曲線非常吻合,ease-out (即 cubic-bezier(0, 0, .58, 1))的貝塞爾曲線為

曲線圖來自 在線繪製貝塞爾曲線網站。
其中,圖表中的縱坐標是指 動畫推進的進程,橫坐標是指 時間,原點坐標為 (0, 0),終點坐標為 (1, 1),假設動畫持續時間為 2 秒,(1, 1) 坐標點則代表動畫啟動後 2 秒時動畫執行完畢(100%)。根據圖表可以得出,時間越往後動畫進程的推進速度越慢,符合勻減速運動的特性。
我們試試實踐應用 ease-out 速度曲線:

很明顯,這樣的速度曲線過於線性平滑,減速效果不明顯。我們參考 iOS 滾動回彈的效果重複測試,調整貝塞爾曲線的參數為 cubic-bezier(.17, .89, .45, 1):

調整曲線後的效果理想很多:

回彈
接下來模擬慣性滾動時觸碰到容器邊界觸發回彈的情況。
我們基於滑塊模型來模擬這樣的場景:滑塊左端與一根彈簧連接,彈簧另一端固定在牆體上,在滑塊向右滑動的過程中,當滑塊到達臨界點(彈簧即將發生形變時)而速度還沒有降到 0m/s 時,滑塊會繼續滑動並拉動彈簧使其發生形變,同時滑塊會受到彈簧的反拉力作減速運動(動能轉化為內能);當滑塊速度降為 0m/s 時,此時彈簧的形變數最大,由於彈性特質彈簧會恢復原狀(內能轉化成動能),並拉動滑塊反向(左)運動。
類似地,回彈過程也可以分為下面兩個階段:
-
滑塊拉動彈簧往右做變減速運動;
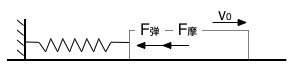
此階段滑塊受到摩擦力 F摩 和越來越大的彈簧拉力 F彈 共同作用,加速度越來越大,導致速度降為 0m/s 的時間會非常短。
-
彈簧恢復原狀,拉動滑塊向左做先變加速後變減速運動;

此階段滑塊受到的摩擦力
F摩和越來越小的彈簧拉力F彈相互抵消,剛開始F彈 > F摩,滑塊做加速度越來越小的變加速運動;隨後F彈 < F摩,滑塊做加速度越來越大的變減速運動,直至最終靜止。這裡為了方便實際計算,我們不妨假設一個理想狀態:當滑塊靜止時彈簧剛好恢復形變。
回彈距離
根據上面的模型分析,回彈的第一階段做加速度越來越大的變減速直線運動,不妨設此階段的初速度為 v0,末速度為 v1,那麼可以與滑塊位移建立關係:

其中 a 為加速度變數,這裡暫不展開討論。那麼,根據物理學的彈性模型,第二階段的回彈距離為

微積分都來了,簡直沒法計算……
然而,我們可以根據運動模型適當簡化 S回彈 值的計算。由於 回彈第二階段的加速度 是大於 非回彈慣性滾動階段的加速度(F彈 + F摩 > F摩)的,不妨設非回彈慣性滾動階段的總距離為 S滑,那麼

因此,我們可以設置一個較為合理的常量 B,使其滿足這樣的等式:

經大量實踐得出,常量
B的合理值為 10。
回彈速度曲線
觸發回彈的整個慣性滾動軌跡可以拆分成三個運動階段:

然而,如果要把階段 a 和階段 b 準確描繪成 CSS 動畫是有很高的複雜度的:
- 階段
b中的變減速運動難以準確描繪; - 這兩個階段雖運動方向相同但動畫速度曲線不連貫,很容易造成用戶體驗斷層;
為了簡化流程,我們把階段 a 和 b 合併成一個運動階段,那麼簡化後的軌跡就變成:

鑒於在階段 a 末端的反向加速度會越來越大,所以此階段滑塊的速度驟減同比非回彈慣性滾動更快,對應的貝塞爾曲線末端就會更陡。我們選擇一條較為合理的曲線 cubic-bezier(.25, .46, .45, .94):

對於階段 b,滑塊先變加速後變減速,與 ease-in-out 的曲線有點類似,實踐嘗試:

仔細觀察,我們發現階段 a 和階段 b 的銜接不夠流暢,這是由於 ease-in-out 曲線的前半段緩入導致的。所以,為了突出效果我們選擇只描繪變減速運動的階段 b 末段。貝塞爾曲線調整為 cubic-bezier(.165, .84, .44, 1)

實踐效果:

由於 gif 轉格式導致部分掉幀,示例效果看起來會有點卡頓,建議直接體驗 demo
CSS 動效時長
我們對 iOS 的滾動回彈效果做多次測量,定義出體驗良好的動效時長參數。在一次慣性滾動中,可能會出現下面兩種情況,對應的動效時間也不一樣:
-
沒有觸發回彈
慣性滾動的合理持續時間為
2500ms。 -
觸發回彈
對於階段
a,當S回彈大於某個關鍵閾值時定義為 強回彈,動效時長為400ms;反之則定義為 弱回彈,動效時長為800ms。而對於階段
b,反彈的持續時間為500ms較為合理。
啟停條件
前文中有提到,如果把用戶滾動頁面元素的整個過程都納入計算範圍是非常不合理的。不難想像,當用戶以非常緩慢的速度使元素滾動比較大的距離,這種情況下元素動量非常小,理應不觸發慣性滾動。因此,慣性滾動的觸發是有條件的。
-
啟動條件
慣性滾動的啟動需要有足夠的動量。我們可以簡單地認為,當用戶滾動的距離足夠大(大於
15px)和持續時間足夠短(小於300ms)時,即可產生慣性滾動。換成程式語言就是,最後一次touchmove事件觸發的時間和touchend事件觸發的時間間隔小於300ms,且兩者產生的距離差大於15px時認為可啟動慣性滾動。 -
暫停時機
當慣性滾動未結束(包括處於回彈過程),用戶再次觸碰滾動元素時,我們應該暫停元素的滾動。在實現原理上,我們需要通過
getComputedStyle和getPropertyValue方法獲取當前的transform: matrix()矩陣值,抽離出元素的水平 y 軸偏移量後重新調整translate的位置。
示例程式碼
基於 vuejs 提供了部分關鍵程式碼,也可以直接訪問 codepen demo 體驗效果(完整程式碼)。
<html>
<body>
<div id="app"></div>
<template id="tpl">
<div
ref="wrapper"
@touchstart.prevent="onStart"
@touchmove.prevent="onMove"
@touchend.prevent="onEnd"
@touchcancel.prevent="onEnd"
@transitionend="onTransitionEnd">
<ul ref="scroller" :style="scrollerStyle">
<li v-for="item in list">{{item}}</li>
</ul>
</div>
</template>
<script>
new Vue({
el: '#app',
template: '#tpl',
computed: {
list() {},
scrollerStyle() {
return {
'transform': `translate3d(0, ${this.offsetY}px, 0)`,
'transition-duration': `${this.duration}ms`,
'transition-timing-function': this.bezier,
};
},
},
data() {
return {
minY: 0,
maxY: 0,
wrapperHeight: 0,
duration: 0,
bezier: 'linear',
pointY: 0, // touchStart 手勢 y 坐標
startY: 0, // touchStart 元素 y 偏移值
offsetY: 0, // 元素實時 y 偏移值
startTime: 0, // 慣性滑動範圍內的 startTime
momentumStartY: 0, // 慣性滑動範圍內的 startY
momentumTimeThreshold: 300, // 慣性滑動的啟動 時間閾值
momentumYThreshold: 15, // 慣性滑動的啟動 距離閾值
isStarted: false, // start鎖
};
},
mounted() {
this.$nextTick(() => {
this.wrapperHeight = this.$refs.wrapper.getBoundingClientRect().height;
this.minY = this.wrapperHeight - this.$refs.scroller.getBoundingClientRect().height;
});
},
methods: {
onStart(e) {
const point = e.touches ? e.touches[0] : e;
this.isStarted = true;
this.duration = 0;
this.stop();
this.pointY = point.pageY;
this.momentumStartY = this.startY = this.offsetY;
this.startTime = new Date().getTime();
},
onMove(e) {
if (!this.isStarted) return;
const point = e.touches ? e.touches[0] : e;
const deltaY = point.pageY - this.pointY;
this.offsetY = Math.round(this.startY + deltaY);
const now = new Date().getTime();
// 記錄在觸發慣性滑動條件下的偏移值和時間
if (now - this.startTime > this.momentumTimeThreshold) {
this.momentumStartY = this.offsetY;
this.startTime = now;
}
},
onEnd(e) {
if (!this.isStarted) return;
this.isStarted = false;
if (this.isNeedReset()) return;
const absDeltaY = Math.abs(this.offsetY - this.momentumStartY);
const duration = new Date().getTime() - this.startTime;
// 啟動慣性滑動
if (duration < this.momentumTimeThreshold && absDeltaY > this.momentumYThreshold) {
const momentum = this.momentum(this.offsetY, this.momentumStartY, duration);
this.offsetY = Math.round(momentum.destination);
this.duration = momentum.duration;
this.bezier = momentum.bezier;
}
},
onTransitionEnd() {
this.isNeedReset();
},
momentum(current, start, duration) {
const durationMap = {
'noBounce': 2500,
'weekBounce': 800,
'strongBounce': 400,
};
const bezierMap = {
'noBounce': 'cubic-bezier(.17, .89, .45, 1)',
'weekBounce': 'cubic-bezier(.25, .46, .45, .94)',
'strongBounce': 'cubic-bezier(.25, .46, .45, .94)',
};
let type = 'noBounce';
// 慣性滑動加速度
const deceleration = 0.003;
// 回彈阻力
const bounceRate = 10;
// 強弱回彈的分割值
const bounceThreshold = 300;
// 回彈的最大限度
const maxOverflowY = this.wrapperHeight / 6;
let overflowY;
const distance = current - start;
const speed = 2 * Math.abs(distance) / duration;
let destination = current + speed / deceleration * (distance < 0 ? -1 : 1);
if (destination < this.minY) {
overflowY = this.minY - destination;
type = overflowY > bounceThreshold ? 'strongBounce' : 'weekBounce';
destination = Math.max(this.minY - maxOverflowY, this.minY - overflowY / bounceRate);
} else if (destination > this.maxY) {
overflowY = destination - this.maxY;
type = overflowY > bounceThreshold ? 'strongBounce' : 'weekBounce';
destination = Math.min(this.maxY + maxOverflowY, this.maxY + overflowY / bounceRate);
}
return {
destination,
duration: durationMap[type],
bezier: bezierMap[type],
};
},
// 超出邊界時需要重置位置
isNeedReset() {
let offsetY;
if (this.offsetY < this.minY) {
offsetY = this.minY;
} else if (this.offsetY > this.maxY) {
offsetY = this.maxY;
}
if (typeof offsetY !== 'undefined') {
this.offsetY = offsetY;
this.duration = 500;
this.bezier = 'cubic-bezier(.165, .84, .44, 1)';
return true;
}
return false;
},
// 停止滾動
stop() {
const matrix = window.getComputedStyle(this.$refs.scroller).getPropertyValue('transform');
this.offsetY = Math.round(+matrix.split(')')[0].split(', ')[5]);
},
},
});
</script>
</body>
</html>
參考資料
歡迎關注凹凸實驗室部落格:aotu.io
或者關注凹凸實驗室公眾號(AOTULabs),不定時推送文章:









