堆與優先隊列
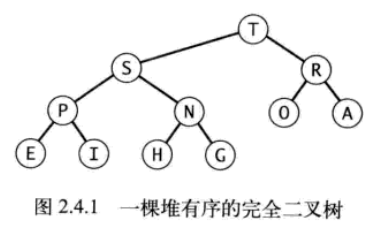
我們經常提到的數據結構大頂堆指的是二叉堆,它是一顆堆有序的完全二叉樹(非葉子結點層都是滿的,最後一層從右向左只能空缺右結點)。其中根節點是所有結點中最大,並且每個父節點都大於其兩個子節點(堆有序)。完全二叉樹底層是用數組實現的,所以它只是邏輯上的一個概念。下圖是一個大頂堆的例子:
那麼給定一個數組怎麼建立大頂堆呢?我們用下面程式碼來說明,建立堆的時間複雜度為O(n)。
1 //建立大頂堆 2 public void creatHeap(int[] arr) { 3 for (int i=0; i<arr.length; i++) { 4 heapInsert(arr, i); 5 } 6 } 7 /** 8 * 某一個元素進堆,元素上浮的過程 9 * @param arr 10 * @param index 11 */ 12 public void heapInsert(int[] arr, int index) { 13 //當前元素大於父節點時,交換 14 while (arr[index] > arr[index / 2 - 1]) { 15 swap(arr, index, index / 2 - 1); 16 // 來到父節點位置繼續比較 17 index = index / 2 - 1; 18 } 19 } 20 21 public void swap(int[] arr, int m, int n) { 22 int temp = arr[m]; 23 arr[m] = arr[n]; 24 arr[n] = temp; 25 }
如果說堆中某個元素變小了,我們可以使用heapify來調整元素的位置,使得堆仍然是大頂堆,heapify實際上是當前元素下沉的過程,具體程式碼如下:
1 /** 2 * 元素下沉過程 3 * @param arr 4 * @param index 當前變小的元素 5 * @param heapSize 堆的大小,小於等於數組的大小 6 */ 7 public void heapify(int[] arr, int index, int heapSize) { 8 //左右孩子結點的索引,數組的索引從0開始 9 int left = 2 * index + 1; 10 int right = left + 1; 11 12 while (left < heapSize) { 13 //從左右孩子中選出大的 14 int largest = right < heapSize && arr[right] > arr[left] ? right : left; 15 //和index比較 16 largest = arr[largest] > arr[index] ? largest : index; 17 //當前變小的元素任然比左右孩子結點大,結束循環 18 if (largest == index) break; 19 //交換 20 swap(arr, largest, index); 21 //更新index位置,來到largest的位置 22 index = largest; 23 //重置left位置,繼續向下比較 24 left = 2 * index + 1; 25 } 26 }
優先隊列本質還是一個隊列,只不過隊列里的元素有優先順序,優先順序高的元素先出隊列。在Java中優先隊列有兩種實現,一種是大頂堆,另外一種是小頂堆。以大頂堆為例:當隊首元素彈出時,優先隊列會自動調整剩下的元素,使其仍是一個大頂堆,時間複雜度為O(nlogn)。具體實現過程就利用了我們上面的heapify方法,同樣給出程式碼說明:
1 public void heapSort(int[] arr) { 2 int len = arr.length; 3 //交換首尾元素,使得彈出的元素在堆中失效,但仍在數組中 4 swap(arr, 0, --len); 5 //不斷地進行heapify操作 6 while (len > 0) { 7 heapify(arr, 0, len); 8 swap(arr, 0, --len); 9 } 10 }
優先隊列可以應用於系統的任務調度,優先順序高的任務先執行,低的在隊列中等候;圖的搜索演算法中也會用到優先隊列,感興趣的童鞋可以閱讀《演算法》第四版具體學習。
參考資料:左程雲演算法初級班
《演算法》第四版