Python機器學習筆記:SVM(2)——SVM核函數
- 2020 年 6 月 6 日
- 筆記
- 機器學習常用演算法及筆記
上一節我學習了完整的SVM過程,下面繼續對核函數進行詳細學習,具體的參考鏈接都在上一篇文章中,SVM四篇筆記鏈接為:
Python機器學習筆記:SVM(1)——SVM概述
Python機器學習筆記:SVM(2)——SVM核函數
Python機器學習筆記:SVM(3)——證明SVM
Python機器學習筆記:SVM(4)——sklearn實現
熱身實例
我在上一節有完整的學習了SVM演算法,為了不讓自己這麼快就忘了,這裡先學習一個實例,回顧一下,並引出核函數的概念。
數據是這樣的:有三個點,其中正例 x1(3, 3),x2(4,3),負例 x3(1,1)
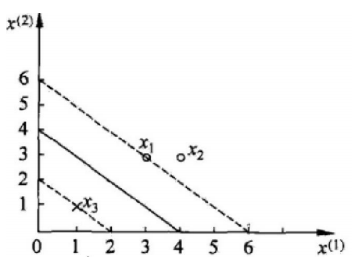
求解:

約束條件為:
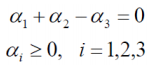
這個約束條件是通過這個得到的(為什麼這裡強調一下呢,因為我們這個例子本身說的就是SVM的求解過程):
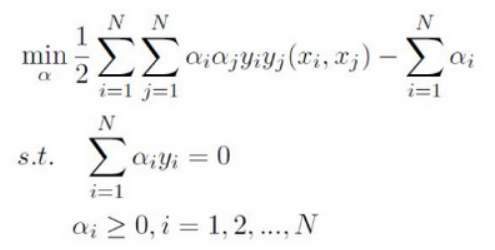
我們可以知道 y1 = +1, y2 = +1 , y3 = -1,同時,代入 α ,則得到:
α1 + α2 – α3=0
下面通過SVM求解實例。
我們將數據代入原式中:
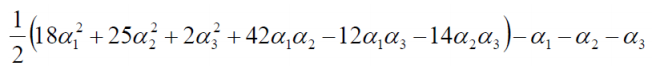
由於 α1 + α2 = α3 化簡可得:

然後分別對 α1 和 α2 求偏導,偏導等於 0 可得: α1 = 1.5 α2 = -1 ,但是我們發現這兩個解並不滿足約束條件 αi >= 0,i=1,2,3,所以解應該在邊界上(正常情況下,我們需要對上式求偏導,進而算出 w,b)。
首先令 α1 = 0,得出 α2 = -2/13 ,α3 = -2/13 (不滿足約束)
再令 α2 = 0,得出 α1 = 0.25 ,α3 = 0.25 (滿足約束)
所以最小值在(0.25, 0,0.25)處取得。
我們將 α 的結果代入求解:
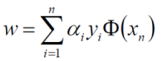
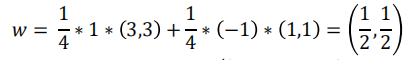
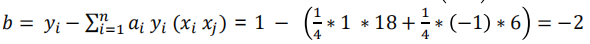
所以我們代入 w b ,求得最終的平面方程為:

熱身完畢,下面學習核函數,為了方便理解我們下面要說的核函數,我在知乎找了一個簡單易懂的故事,讓我們了解支援向量機,更是明白支援向量機的核函數是個什麼鬼,下面看故事。
1,故事分析:支援向量機(SVM)是什麼?
下面故事來源於此(這是源作者鏈接):點擊我即可
在很久以前的情人節,有一個大俠要去救他的愛人,但是魔鬼和他玩了一個遊戲。
魔鬼在桌面上似乎有規律放了兩種顏色的球,說:「你用一根棍分開他們?要求:盡量在放更多球之後,仍然使用」

於是大俠這樣做,幹得不錯吧:
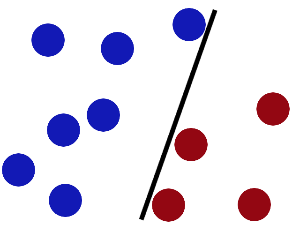
然後魔鬼又在桌上放了更多的球,似乎有一個球站錯了陣營。
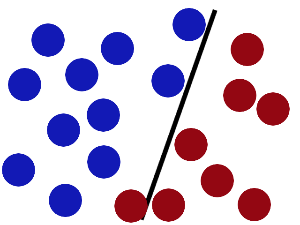
SVM就是試圖把棍放在最佳位置,好讓在棍的兩邊有儘可能大的間隙。
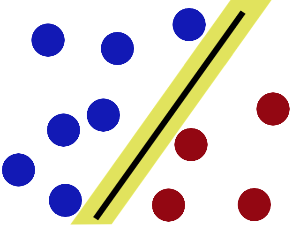
現在即使魔鬼放了更多的球,棍仍然是一個好的分界線。

然後,在SVM工具箱中有另一個更加重要的trick 。魔鬼看到大俠已經學會了一個trick,於是魔鬼給了大俠一個新的挑戰。

現在,大俠沒有棍可以很好地幫他分開這兩種球了,現在怎麼辦,當然像所有武俠片中一樣大俠桌子一拍,球飛到空中。然後憑藉著大俠的輕功,大俠抓起一張紙,插到了兩種球的中間。

現在,從魔鬼的角度看這些球,這些球好像是被一條曲線分開了。
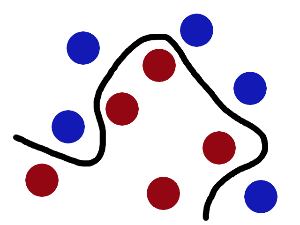
在之後,無聊的大人們,把這些球叫做 「data」,把棍子 叫做 「classifier」, 最大間隙trick 叫做「optimization」, 拍桌子叫做「kernelling」, 那張紙叫做「hyperplane」。
所以說,Support Vector Machine,一個普通的SVM就是一條直線罷了,用來完美劃分linearly separable的兩類。但是這又不是一條普通的直線,這是無數條可以分類的直線當中最完美的,因為它恰好在兩個類的中間,距離兩個類的點都一樣遠。而所謂的Support vector就是這些離分界線最近的點,如果去掉這些點,直線多半是要改變位置的。如果是高維的點,SVM的分界線就是平面或者超平面。其實沒有差,都是一刀切兩塊,我們這裡統一叫做直線。
再理解一下,當一個分類問題,數據是線性可分的,也就是用一根棍就可以將兩種小球分開的時候,我們只要將棍的位置放在讓小球距離棍的距離最大化的位置即可。尋找這個最大間隔的過程,就叫做最優化。但是,顯示往往是殘酷的,一般的數據是線性不可分的。也就是找不到一個棍將兩種小球很好的分類,這時候我們就需要像大俠一樣,將小球排起,用一張紙代替小棍將兩種小球進行分類,想讓數據飛起,我們需要的東西就是核函數(kernel),用於切分小球的紙,就是超平面。
2,核函數的概念
上面故事說明了SVM可以處理線性可分的情況,也可以處理非線性可分的情況。而處理非線性可分的情況是選擇了核函數(kernel),通過將數據映射到高位空間,來解決在原始空間中線性不可分的問題。
我們希望樣本在特徵空間中線性可分,因此特徵空間的好壞對支援向量機的性能至關重要,但是在不知道特徵映射的情況下,我們是不知道什麼樣的核函數是適合的,而核函數也只是隱式的定義了特徵空間,所以,核函數的選擇對於一個支援向量機而言就顯得至關重要,若選擇了一個不合適的核函數,則數據將映射到不合適的樣本空間,從而支援向量機的性能將大大折扣。
所以構造出一個具有良好性能的SVM,核函數的選擇是關鍵。而核函數的選擇包含兩部分工作:一是核函數類型的選擇,二是確定核函數類型後相關參數的選擇。
我們知道,核函數的精妙之處在於不用真的對特徵向量做核映射,而是直接對特徵向量的內積進行變換,而這種變換卻等價於先對特徵向量做核映射然後做內積。
SVM主要是在用對偶理論求解一個二次凸優化問題,其中對偶問題如下:
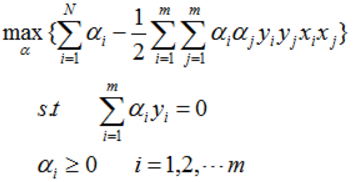
求得最終結果:
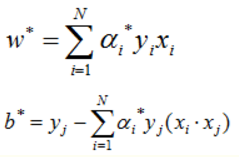
當然這是線性可分的情況,那麼如果問題本身是線性不可分的情況呢?那就是先擴維後再計算。具體來說,在線性不可分的情況下,支援向量機首先在低維空間中完成計算,然後通過核函數將輸入空間映射到高維特徵空間,最終在高維特徵空間中構造出最優分離超平面,從而把平面上本身不好分的非線性數據分開。如下圖所示,一堆數據在二維空間中無法劃分,從而映射到三維空間中劃分:

而在我們遇到核函數之前,如果用原始的方法,那麼在用線性學習器學習一個非線性關係,需要選擇一個非線性特徵集,並且將數據寫成新的表達形式,這等價於應用一個固定的非線性映射,將數據映射到特徵空間,在特徵空間中使用線性學習器。因此,考慮的假設集是這種類型的函數:
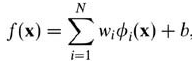
這裡 Φ :X -> F 是從輸入空間到某個特徵空間的映射,這意味著建立非線性學習器分為兩步:
- 1,使用一個非線性映射將數據變換到一個特徵空間 F
- 2,在特徵空間使用線性學習器分類
而由於對偶形式就是線性學習器的一個重要性質,這意味著假設可以表達為訓練點的線性組合,因此決策規則可以用測試點和訓練點的內積來表示:
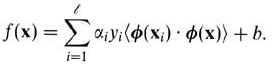
為向量加上核映射後,要求解的最優化問題變為:
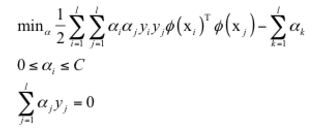
根據核函數滿足的等式條件,它等價於下面的問題:
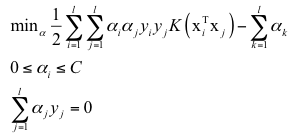
其線性不可分情況的對偶形式如下:
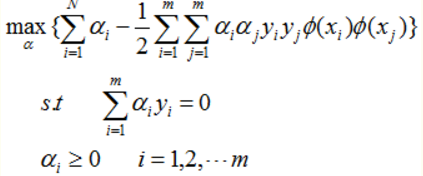
其中 Φ(xi) 表示原來的樣本擴維後的坐標。
最後得到的分類判別函數為:
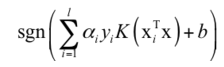
和不用核映射相比,只是求解的目標函數,最後的判定函數對特徵向量的內積做了核函數變換。如果K是一個非線性函數,上面的決策函數則是非線性函數,此時SVM是非線性模型。當訓練樣本很多,支援向量的個數很大的時候,預測時的速度是一個問題,因此很多時候我們會使用線性支援向量機。
3,舉例說明核函數的巧妙之處
下面先從一個小例子來闡述問題。假設我們有兩個數據, x = (x1, x2, x3) y = (y1, y2, y3)。此時在3D空間已經不能對其進行線性劃分了,那麼我們通過一個函數將數據映射到更高維的空間,比如9維的話,那麼 f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3),由於需要計算內積,所以在新的數據在 9 維空間,需要計算 <f(x), f(y)> 的內積,需要花費 O(n^2)。
再具體點,令 x = (1, 2, 3), y = (4, 5, 6),那麼 f(x) = (1, 2, 3, 2, 4, 6, 3, 6, 9),f(y) = (16, 20, 24, 20, 25, 36, 24, 30, 36)
此時: <f(x), f(y)> = 16 + 40 + 72 +40 +100 + 180 + 72 +180 +324 = 1024
對於3D空間這兩個數據,似乎還能計算,但是如果將維數擴大到一個非常大數的時候,計算起來可就不是這麼一點點問題了。
然而,我們發現 K(x, y) = (<x, y>)^2 ,代入上式: K(x, y) = (4 + 10 + 18)^2 = 32^2 = 1024
也就是說 : K(x, y) = (<x, y>)^2 = <f(x), f(y)> 。
但是 K(x, y) 計算起來卻比 <f(x), f(y)> 簡單的多,也就是說只要用 K(x, y)來計算,效果與 <f(x), f(y)> 是一樣的,但是計算效率卻大幅度提高了,如 K(x, y) 是 O(n),而 <f(x), f(y)> 是 O(n^2),所以使用核函數的好處就是,可以在一個低維空間去完成一個高緯度(或者無限維度)樣本內積的計算,比如上面例子中 K(x, y)的3D空間對比 <f(x), f(y)> 的9D空間。
下面再舉個例子來證明一下上面的問題,為了簡單起見,假設所有樣本點都是二維點,其值分別為(x, y),分類函數為:
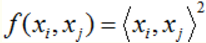
它對應的映射方式為:

可以驗證:任意兩個擴維後的樣本點在3維空間的內積等於原樣本點在二維空間的函數輸出:
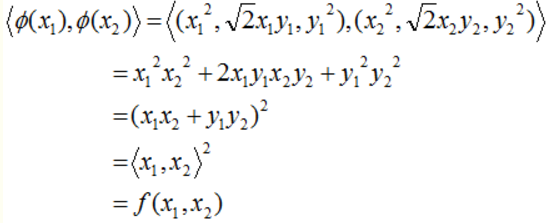
有了這個核函數,以後的高維內積都可以轉換為低維的函數運算了,這裡也就是說只需要計算低維的內積,然後再平方。明顯問題得到解決且複雜度降低極大。總而言之:核函數它本質上隱含了從低維到高維的映射,從而避免直接計算高維的內積。
當然上述例子是多項式核函數的一個特例,其實核函數的種類還有很多,後文會一一介紹。
4,核函數的計算原理
通過上面的例子,我們大概可以知道核函數的巧妙應用了,下面學習一下核函數的計算原理。
如果有一種方法可以在特徵空間中直接計算內積 <Φ(xi , Φ(x)> ,就像在原始輸入點的函數中一樣,就有可能將兩個步驟融合到一起建立一個非線性的學習器,這樣直接計算的方法稱為核函數方法。
設 x 是輸入空間(歐式空間或者離散集合),H為特徵空間(希爾伯特空間),如果存在一個從 x 到 H 的映射:
![]()
核是一個函數 K,對於所有 x, z ∈ χ, 則滿足:

則稱Κ(x,z)為核函數,φ(x)為映射函數,φ(x)∙φ(z)為x,z映射到特徵空間上的內積。
參考網友的理解:任意兩個樣本點在擴維後的空間的內積,如果等於這兩個樣本點在原來空間經過一個函數後的輸出,那麼這個函數就叫核函數。
由於映射函數十分複雜難以計算,在實際中,通常都是使用核函數來求解內積,計算複雜度並沒有增加,映射函數僅僅作為一種邏輯映射,表徵著輸入空間到特徵空間的映射關係。至於為什麼需要映射後的特徵而不是最初的特徵來參與計算,為了更好地擬合是其中一個原因,另外的一個重要原因是樣例可能存在線性不可分的情況,而將特徵映射到高維空間後,往往就可分了。
下面將核函數形式化定義。如果原始特徵內積是 <X , Z>,映射 <Φ(xi • Φ(x)>,那麼定義核函數(Kernel)為:
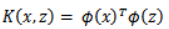
到這裡,我們可以得出結論,如果要實現該節開頭的效果,只需要計算 Φ(x) ,然後計算 Φ(x)TΦ(x)即可,然而這種計算方式是非常低效的。比如最初的特徵是n維的,我們將其映射到 n2 維,然後再計算,這樣需要O(n2 ) 的時間,那麼我們能不能想辦法減少計算時間呢?
先說結論,當然是可以的,畢竟我們上面例子,活生生的說明了一個將需要 O(n2 ) 的時間 轉換為 需要O(n ) 的時間。
先看一個例子,假設x和z都是n維度的,
![]()
展開後,得到:
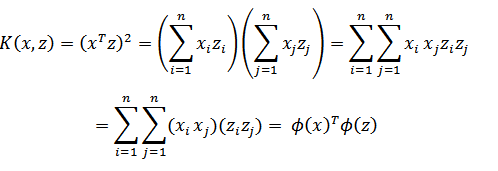
這個時候發現我們可以只計算原始特徵 x 和 z 內積的平方(時間複雜度為O(n)),就等價於計算映射後特徵的內積。也就是說我們不需要花O(n2 ) 的時間了。
現在看一下映射函數(n = 3),根據上面的公式,得到:

也就是說核函數 Κ(x,z) = (xTz)2 只能選擇這樣的 φ 作為映射函數時才能夠等價於映射後特徵的內積。
再看另外一個核函數,高斯核函數:

這時,如果 x 和 z 很相近 (||x – z || 約等於 0),那麼核函數值為1,如果 x 和 z 相差很大(||x – z || >> 0),那麼核函數值約等於0.由於這個函數類似於高斯分布,因此稱為高斯核函數,也叫做徑向基函數(Radial Basis Function 簡稱為RBF)。它能夠把原始特徵映射到無窮維。
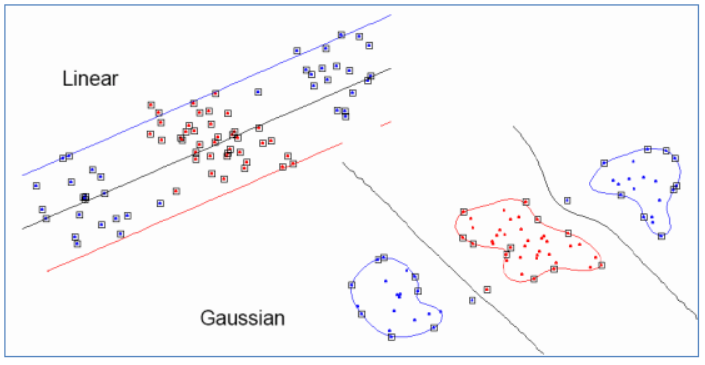
下面有張圖說明在低維線性不可分時,映射到高維後就可分了,使用高斯核函數。
注意,使用核函數後,怎麼分類新來的樣本呢?線性的時候我們使用SVM學習出w和b,新來樣本x的話,我們使用 wTx + b 來判斷,如果值大於等於1,那麼是正類,小於等於是負類。在兩者之間,認為無法確定。如果使用了核函數後,wTx + b 就變成了 wTΦ(x) + b,是否先要找到 Φ(x) ,然後再預測?答案肯定不是了,找 Φ(x) 很麻煩,回想我們之前說過的。
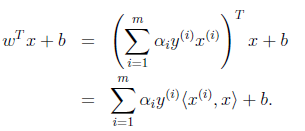
只需將 <(x(i) , x> 替換成 (x(i) , x),然後值的判斷同上。
4.1 核函數有效性的判定
問題:給定一個函數K,我們能否使用K來替代計算 Φ(x)TΦ(x),也就說,是否能夠找出一個 Φ,使得對於所有的x和z,都有 K(x, z) = Φ(x)TΦ(x),即比如給出了 K(x, z) = (xTz)2,是否能夠認為K是一個有效的核函數。
下面來解決這個問題,給定m個訓練樣本(x(1),x(2), ….,x(m)),每一個x(i) 對應一個特徵向量。那麼,我們可以將任意兩個 x(i) 和 x(j) 帶入K中,計算得到Kij = K(x(i), x(j))。i 可以從1到m,j 可以從1到m,這樣可以計算出m*m的核函數矩陣(Kernel Matrix)。為了方便,我們將核函數矩陣和 K(x, z) 都使用 K 來表示。如果假設 K 是有效地核函數,那麼根據核函數定義:
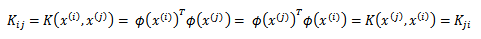
可見,矩陣K應該是個對稱陣。讓我們得出一個更強的結論,首先使用符號ΦK(x)來表示映射函數 Φ(x) 的第 k 維屬性值。那麼對於任意向量 z,得:
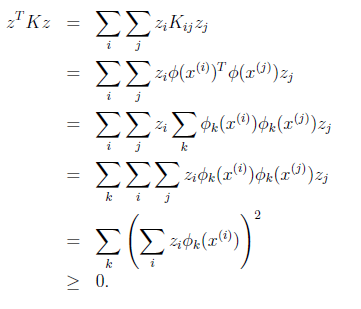
最後一步和前面計算 K(x, z) = (xTz)2 時類似。從這個公式我們可以看出,如果K是個有效的核函數(即 K(x, z) 和 Φ(x)TΦ(z)等價),那麼,在訓練集上得到的核函數矩陣K應該是半正定的(K>=0)。這樣我們得到一個核函數的必要條件:K是有效的核函數 ==> 核函數矩陣K是對稱半正定的。
Mercer定理表明為了證明K是有效的核函數,那麼我們不用去尋找 Φ ,而只需要在訓練集上求出各個 Kij,然後判斷矩陣K是否是半正定(使用左上角主子式大於等於零等方法)即可。
5,核函數:如何處理非線性數據
來看個核函數的例子。如下圖所示的兩類數據,分別分布為兩個圓圈的形狀,這樣的數據本身就是線性不可分的,此時我們該如何把這兩類數據分開呢?
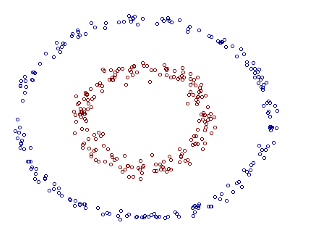
事實上,上圖所示的這個數據集,是用兩個半徑不同的圓圈加上了少量的噪音生成得到的,所以,一個理想的分界應該是「圓圈」 而不是「一條線」(超平面)。如果用 X1 和 X2 來表示這個二維平面的兩個坐標的話,我們知道一條二次曲線(圓圈是二次曲線的一種特殊情況)的方程可以寫作這樣的形式:
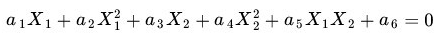
注意上面的形式,如果我們構造另外一個五維的空間,其中五個坐標的值分別為:
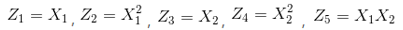
那麼顯然,上面的方程在新的坐標系下可以寫做:
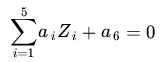
關於新的坐標 Z,這正是一個 hyper plane 的方程!也就是說,如果我們做一個映射:
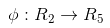
將X按照上面的規則映射為 Z,那麼在新的空間中原來的數據將變成線性可分的,從而使用之前我們推導的線性分類演算法就可以進行處理了。這正是Kernel方法處理非線性問題的基本思想。
再進一步描述 Kernel 的細節之前,不妨再來看看上述例子在映射過後的直觀形態。當然,我們無法將五維空間畫出來,不過由於我這裡生成數據的時候用了特殊的情形,所以這裡的超平面實際的方程是這個樣子的(圓心在X2軸上的一 個正圓):

因此我只需要把它映射到下面這樣一個三維空間中即可:

下圖即是映射之後的結果,將坐標軸經過適當的旋轉,就可以很明顯的看出,數據是可以通過一個平面來分開的
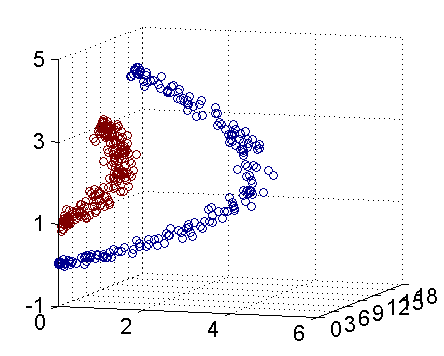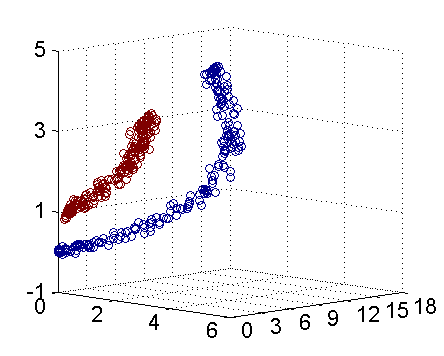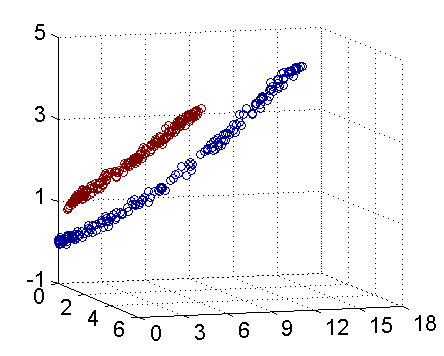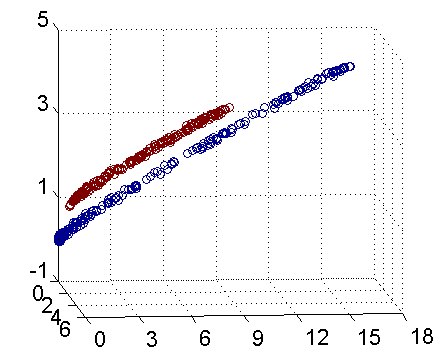
核函數相當於把原來的分類函數:
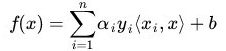
映射成:
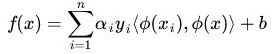
而其中的 α 可以通過求解如下 dual 問題而得到的:

這樣一來問題就解決了嗎?似乎是的:拿到非線性數據,就找一個映射(Φ(•),然後一股腦把原來的數據映射到新空間中,再做線性SVM即可。不過事實上問題好像沒有這麼簡單)。
細想一下,剛才的方法是不是有問題:
在最初的例子里,我們對一個二維空間做映射,選擇的新空間是原始空間的所有一階和二階的組合,得到了五個維度;
如果原始空間是三維(一階,二階和三階的組合),那麼我們會得到:3(一次)+3(二次交叉)+3(平方)+3(立方)+1(x1 * x2 * x3) + 2*3(交叉,一個一次一個二次,類似 x1*x2^2)=19 維的新空間,這個數目是呈指數級爆炸性增長的,從而勢必這給 Φ(•) 的計算帶來非常大的困難,而且如果遇到無窮維的情況,就根本無從計算了。
這個時候,可能就需要Kernel出馬了。
不妨還是從最開始的簡單例子觸發,設兩個向量為:
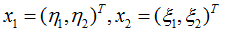
而 Φ(•) 即是前面說的五維空間的映射,因此映射過後的內積為:
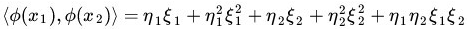
(公式說明:上面的這兩個推導過程中,所說的前面的五維空間的映射,這裡說的便是前面的映射方式,回顧下之前的映射規則,再看看那個長的推導式,其實就是計算x1,x2各自的內積,然後相乘相加即可,第二個推導則是直接平方,去掉括弧,也很容易推出來)
另外,我們又注意到:
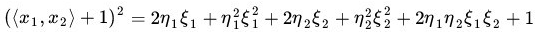
二者有很多相似的地方,實際上,我們只要把某幾個維度線性縮放一下,然後再加上一個常數維度,具體來說,上面這個式子的計算結果實際上和映射
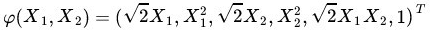
之後的內積 <Φ(xi • Φ(x)> 的結果是相等的,那麼區別在什麼地方呢?
- 1,一個是映射到高維空間中,然後再根據內積的公式進行計算
- 2,另一個則直接在原來的低維空間中進行計算,而不需要顯式地寫出映射後的結果
(公式說明:上面之中,最後的兩個式子,第一個算式,是帶內積的完全平方式,可以拆開,然後,再通過湊一個得到,第二個算式,也是根據第一個算式湊出來的)
回想剛才提到的映射的維度爆炸,在前一種方法已經無法計算的情況下,後一種方法卻依舊能從容處理,甚至是無窮維度的情況也沒有問題。
我們把這裡的計算兩個向量在隱式映射過後的空間中的內積的函數叫做核函數(kernel Function),例如,在剛才的例子中,我們的核函數為:

核函數能簡化映射空間中的內積運算——剛好「碰巧」的是,在我們的SVM里需要計算的地方數據向量總是以內積的形式出現的。對比剛才我們上面寫出來的式子,現在我們的分類函數為:

其中 α 由如下 dual 問題計算而得:

這樣一來計算的問題就算解決了,避免了直接在高維空間中進行計算,而結果卻是等價的!當然,因為我們這裡的例子非常簡單,所以可以手工構造出對應於 Φ(•) 的核函數出來,如果對於任意一個映射,想要構造出對應的核函數就非常困難了。
6,核函數的本質
下面概況一下核函數的意思:
- 1,實際上,我們會經常遇到線性不可分的樣例,此時,我們的常用做法是把樣例特徵映射到高位空間中去(比如之前有個例子,映射到高維空間後,相關特徵便被分開了,也就達到了分類的目的)
- 2,進一步,如果凡是遇到線性不可分的樣例,一律映射到高維空間,那麼這個維度大小是會高到可怕的(甚至是無窮維),所以核函數就隆重出場了,核函數的價值在於它雖然也是將特徵進行從低維到高維的轉換,但核函數絕就絕在它事先在低維上進行計算,而將實質上的分類效果表現在了高維上,也就是上文所說的避免了直接在高維空間中的複雜計算。
下面引用這個例子距離下核函數解決非線性問題的直觀效果。
假設現在你是一個農場主,圈養了一批羊群,但為了預防狼群襲擊羊群,你需要搭建一個籬笆來把羊群圈起來。但是籬笆應該建在哪裡呢?你很可能需要依據羊群和狼群的位置搭建一個「分類器」,比如下圖這幾種不同的分類器,我們可以看到SVM完成了一個很完美的解決方案。
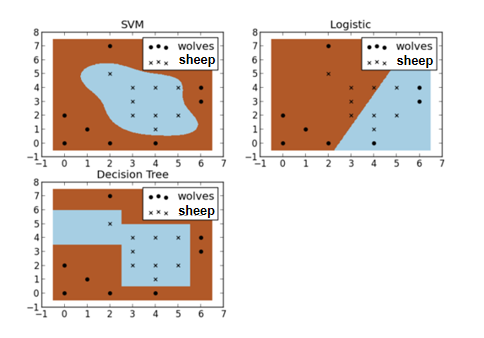
這個例子側面簡單說明了SVM使用非線性分類器的優勢,而邏輯模式以及決策樹模式都是使用了直線方法。
7,幾種常見的核函數
核函數有嚴格的數學要求,所以設計一個核函數是非常困難的,科學家們經過很多很多嘗試也就只嘗試出來幾個核函數,所以我們就不要在這方面下無用功了,直接拿這常見的幾個核函數使用就OK。
下面來分別學習一下這幾個常見的核函數。
7.1 線性核(Linear Kernel )
基本原理:實際上就是原始空間中的內積

這個核存在的主要目的是使得「映射後空間中的問題」 和 「映射前空間中的問題」 兩者在形式上統一起來了(意思是說:我們有的時候,寫程式碼或者寫公式的時候,只要寫個模板或者通用表達式,然後再代入不同的核,便可以了。於此,便在形式上統一了起來,不用再找一個線性的和一個非線性的)
線性核,主要用於線性可分的情況,我們可以看到特徵空間到輸入空間的維度是一樣的。在原始空間中尋找最優線性分類器,具有參數少速度快的優勢。對於線性可分數據,其分類效果很理想。因此我們通常首先嘗試用線性核函數來做分類,看看效果如何,如果不行再換別的。
優點:
- 方案首選,奧多姆剃刀定理
- 簡單,可以快速解決一個QP問題
- 可解釋性強:可以輕易知道哪些feature是重要的
限制:
- 只能解決線性可分問題
7.2 多項式核(Polynomial Kernel)
基本原理:依靠升維使得原本線性不可分的數據線性可分。

多項式核函數可以實現將低維的輸入空間映射到高維的特徵空間。多項式核適合於正交歸一化(向量正交且模為1)數據,屬於全局核函數,允許相距很遠的數據點對核函數的值有影響。參數d越大,映射的維度越高,計算量就會越大。
優點:
- 可解決非線性問題
- 可通過主觀設置Q來實現總結的預判
缺點:
- 多項式核函數的參數多,當多項式的階數d比較高的是,由於學習複雜性也會過高,易出現「過擬合」現象,核矩陣的元素值將趨於無窮大或者無窮小,計算複雜度會大道無法計算。
7.3 高斯核(Gaussian Kernel)/ 徑向基核函數(Radial Basis Function)
徑向基核函數是SVM中常用的一個核函數。徑向基函數是一個採用向量作為自變數的函數,能夠基於向量距離運算輸出一個標量。
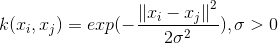
也可以寫成如下格式:
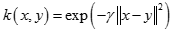
徑向基函數是指取值僅僅依賴於特定點距離的實值函數,也就是:

任意一個滿足上式特性的函數 Φ 都叫徑向量函數,標準的一般使用歐氏距離,儘管其他距離函數也是可以的。所以另外兩個比較常用的核函數,冪指數核,拉普拉斯核也屬於徑向基核函數。此外不太常用的徑向基核還有ANOVA核,二次有理核,多元二次核,逆多元二次核。
高斯徑向基函數是一種局部性強的核函數,其可以將一個樣本映射到一個更高維的空間內,該核函數是應用最廣的一個,無論大樣本還是小樣本都有比較好的性能,而且其相對於多項式核函數參數要少,因此大多數情況下在不知道用什麼樣的核函數的時候優先使用高斯核函數。
徑向基核函數屬於局部核函數,當數據點距離中心點變遠時,取值會變小。高斯徑向基核對數據中存在的雜訊有著較好的抗干擾能力,由於其很強的局部性,其參數決定了函數作用範圍,隨著參數 σ 的增大而減弱。
優點:
- 可以映射到無線維
- 決策邊界更為多樣
- 只有一個參數,相比多項式核容易選擇
缺點:
- 可解釋性差(無限多維的轉換,無法算出W)
- 計算速度比較慢(當解決一個對偶問題)
- 容易過擬合(參數選不好時容易overfitting)
上述所講的徑向核函數表達式:
冪指數核(Exponential Kernel)
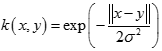
拉普拉斯核(LaplacIan Kernel)
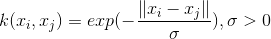
ANOVA 核(ANOVA Kernel)
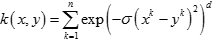
二次有理核(Rational Quadratic Kernel)
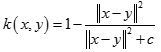
多元二次核(Multiquadric Kernel)
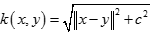
逆多元二次核(Inverse Multiquadric Kernel)
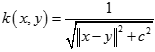
7.4 Sigmoid核
Sigmoid核函數來源於神經網路,被廣泛用於深度學習和機器學習中
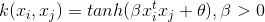
採用Sigmoid函數作為核函數時,支援向量機實現的就是一種多層感知器神經網路,應用SVM方法,隱含層節點數目(它確定神經網路的結構),隱含層節點對輸入節點的權重都是在設計(訓練)的過程中自動確定的。而且支援向量機的理論基礎決定了它最終求得的是全局最優值而不是局部最優值,也保證了它對未知樣本的良好泛化能力而不會出現過學習線性。
8,核函數的選擇
8.1,先驗知識
利用專家的先驗知識預先選定核函數
8.2,交叉驗證
採取Cross-Validation方法,即在進行核函數選取時,分別試用不同的核函數,歸納誤差最小的核函數就是最好的核函數。如針對傅里葉核,RBF核,結合訊號處理問題中的函數回歸問題,通過模擬實驗,對比分析了在相同數據條件下,採用傅里葉核的SVM要比採用RBF核的SVM誤差小很多。
8.3,混合核函數
採用由Smits等人提出的混合核函數方法,該方法較之前兩者是目前選取核函數的主流方法,也是關於如何構建核函數的又一開創性的工作,將不同的核函數結合起來後有更好的特性,這是混合核函數方法的基本思想。
8.4,經驗
當樣本特徵很多時,特徵的維度很高,這是往往樣本線性可分,可考慮用線性核函數的SVM或者LR(如何不考慮核函數,LR和SVM都是線性分類演算法,也就是說他們的分類決策面都是線性的)
當樣本的數量很多,但特徵較少時,可以手動添加一些特徵,使樣本線性可分,再考慮用線性核函數的SVM或者LR
當樣本特徵維度不高時,樣本數量也不多時,考慮使用高斯核函數(RBF核函數的一種,指數核函數和拉普拉斯核函數也屬於RBF核函數)
8.5,吳恩達給出的選擇核函數的方法
如果特徵的數量大道和樣本數量差不多,則選用LR或者線性核的SVM
如果特徵的數量小,樣本的數量正常,則選用SVM+ 高斯核函數
如果特徵的數量小,而樣本的數量很大,則需要手工添加一些特徵從而變成第一種情況
8.6 核函數選擇的例子
這裡簡單說一下核函數與其他參數的作用(後面會詳細學習關於使用Sklearn學習SVM):
- kernel=’linear’ 時,C越大分類效果越好,但有可能會過擬合(default C=1)
- kernel=’rbf’時,為高斯核,gamma值越小,分類介面越連續;gamma值越大,分類介面越「散」,分類效果越好,但有可能會過擬合。
我們來看一個簡單的例子,數據為[-5.0 , 9.0] 的隨機數組,函數如下 :
![]()
下面分別使用三種核SVR:兩種乘法係數高斯核rbf和一種多項式核poly。程式碼如下:
from sklearn import svm
import numpy as np
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings('ignore')
X = np.arange(-5.0 , 9.0 , 0.1)
# print(X)
X = np.random.permutation(X)
# print('1X:',X)
X_ = [[i] for i in X]
b = 0.5
y = 0.5 * X ** 2.0 + 3.0 * X + b + np.random.random(X.shape) * 10.0
y_ = [i for i in y]
# degree = 2 , gamma=, coef0 =
rbf1 = svm.SVR(kernel='rbf',C=1,)
rbf2 = svm.SVR(kernel='rbf',C=20,)
poly = svm.SVR(kernel='poly',C=1,degree=2)
rbf1.fit(X_ , y_)
rbf2.fit(X_ , y_)
poly.fit(X_ , y_)
result1 = rbf1.predict(X_)
result2 = rbf2.predict(X_)
result3 = poly.predict(X_)
plt.plot(X,y,'bo',fillstyle='none')
plt.plot(X,result1,'r.')
plt.plot(X,result2,'g.')
plt.plot(X,result3,'b.')
plt.show()
結構圖如下:

藍色是poly,紅色是c=1的rbf,綠色c=20的rbf。其中效果最好的是C=20的rbf。如果我們知道函數的表達式,線性規劃的效果更好,但是大部分情況下我們不知道數據的函數表達式,因此只能慢慢實驗,SVM的作用就在這裡了。
9,總結
支援向量機是一種分類器。之所以稱為「機」是因為它會產生一個二值決策結果,即它是一種決策「機」。支援向量機的泛化錯誤率較低,也就是說它具有良好的學習能力,且學到的結果具有很好的推廣性。這些優點使得支援向量機十分流行,有些人認為它是監督學習中最好的定式演算法。
支援向量機視圖通過求解一個二次優化問題來最大化分類間隔。在過去,訓練支援向量機常採用非常複雜並且低效的二次規劃求解方法。John Platt 引入了SMO演算法,此演算法可以通過每次只優化2個 α 值來加快SVM的訓練速度。
核方法或者說核技巧會將數據(有時候是非線性數據)從一個低維空間映射到一個高維空間,可以將一個在低維空間中的非線性問題轉化為高維空間下的線性問題來求解。核方法不止在SVM中適用,還可以用於其他演算法。而其中的徑向基函數是一個常用的度量兩個向量距離的核函數。

