三、排序之冒泡、插入、選擇
一、衡量一個排序演算法
1.1、排序演算法的執行效率
- 最好情況、最壞情況、平均情況時間複雜度
- 時間複雜度的係數、常數 、低階
時間複雜度反應的是數據規模 n 很大的時候的一個增長趨勢,所以它表示的時候會忽略係數、常數、低階。
但是實際的軟體開發中,我們排序的可能是10個、 100個、 1000個這樣規模很小的數據,所以,在對同一階時間複雜度的排序演算法性能對比的時候,我們就要把係數、常數、低階也考慮進來。 - 比較次數和交換(或移動)次數
冒泡、插入、選擇都是基於比較的排序演算法。基於比較的排序演算法的執行過程,會涉及兩種操作,一種是元素比較大小,另一種是元素交換或移動。
所以,如果我們在分析排序演算法的執行效率的時候,應該把比較次數和交換(或移動)次數也考慮進去。
1.2、排序演算法的記憶體消耗
- 演算法的記憶體消耗可以通過空間複雜度來衡量,排序演算法也不例外。
- 不過,針對排序演算法的空間複雜度,還有一個新的概念, 原地排序(Sorted in place)。
原地排序演算法,就是特指空間複雜度是 O(1) 的排序演算法。我們今天講的三種排序演算法,冒泡、插入、選擇原地排序演算法。
1.3、排序演算法的穩定性
- 如果待排序的序列中存在值相等的元素,經過排序之後,相等元素之間原有的先後順序不變。
- 比如一組數據 2, 9, 3, 4, 8, 3,按照大小排序之後就是 2, 3, 3, 4, 8, 9。
- 這組數據里有兩個 3。經過某種排序演算法排序之後,如果兩個 3 的前後順序沒有改變,那我們就把這種排序演算法叫作穩定的排序演算法。
- 如果前後順序發生變化,那對應的排序演算法就叫作不穩定的排序演算法。

二、冒泡排序
- 冒泡排序只會操作相鄰的兩個數據。每次冒泡操作都會對相鄰的兩個元素進行比較。
- 看是否滿足大小關係要求。如果不滿足就讓它倆互換。一次冒泡會讓至少一個元素移動到它應該在的位置。
- 重複 n 次,就完成了 n 個數據的排序工作。
- 冒泡的過程只涉及相鄰數據的交換操作,只需要常量級的臨時空間,所以它的空間複雜度為 O(1),是一個原地排序演算法。
- 在冒泡排序中,只有交換才可以改變兩個元素的前後順序。為了保證冒泡排序演算法的穩定性,當有相鄰的兩個元素大小相等的時候。
- 我們不做交換,相同大小的數據在排序前後不會改變順序,所以冒泡排序是穩定的排序演算法。
- 最好情況下,要排序的數據已經是有序的了,我們只需要進行一次冒泡操作,就可以結束了,所以最好情況時間複雜度是 O(n)。
- 而最壞的情況是,要排序的數據剛好是倒序排列的,我們需要進行 n 次冒泡操作,所以最壞情況時間複雜度為 O(n²)。
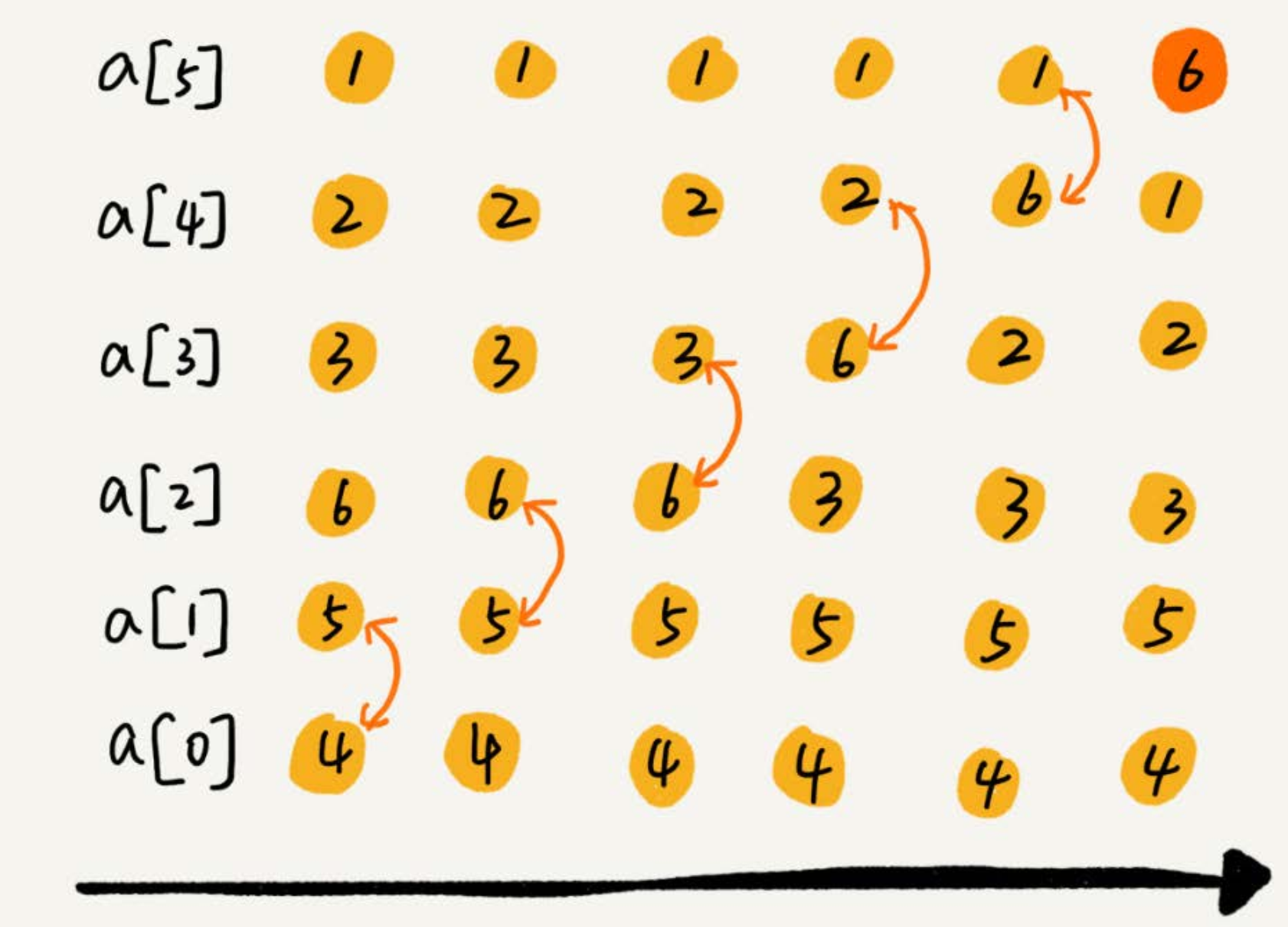
可以看出,經過一次冒泡操作之後, 6這個元素已經存儲在正確的位置上。要想完成所有數據的排序,我們只要進行6次這樣的冒泡操作就行了。

public static void bubbleSort(int[] arr) {
if (arr.length <= 1)
return;
for (int i = 0; i < arr.length; i++) {
boolean b = false;
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
b = true;
}
}
if (!b) {
break;
}
}
}
三、插入排序(Insertion Sort)
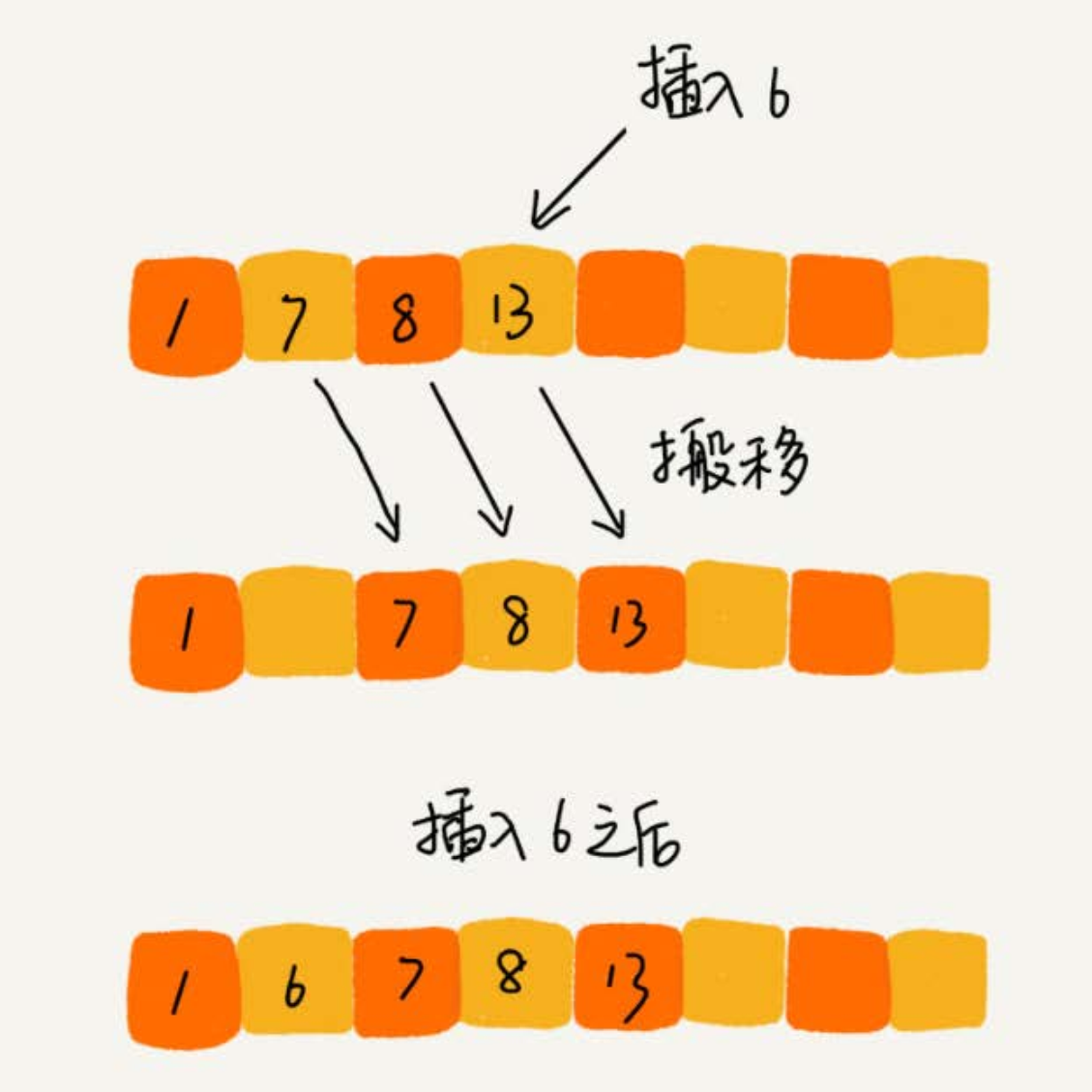
- 將數組中的數據分為兩個區間, 已排序區間和未排序區間。
- 初始已排序區間只有一個元素,就是數組的第一個元素。
- 插入演算法的核心思想是取未排序區間中的元素,在已排序區間中找到合適的插入位置將其插入,並保證已排序區間數據一直有序。
- 重複這個過程,直到未排序區間中元素為空,演算法結束。

- 插入排序演算法的運行並不需要額外的存儲空間,所以空間複雜度是 O(1),也就是說,這是一個原地排序演算法。
- 在插入排序中,對於值相同的元素,我們可以選擇將後面出現的元素,插入到前面出現元素的後面,這樣就可以保持原有的前後順序不變,
- 所以插入排序是穩定的排序演算法。
- 如果要排序的數據已經是有序的,我們並不需要搬移任何數據。
- 如果我們從尾到頭在有序數據組裡面查找插入位置,每次只需要比較一個數據就能確定插入的位置。
- 所以這種情況下,最好是時間複雜度為 O(n)。注意,這裡是從尾到頭遍歷已經有序的數據。
- 如果數組是倒序的,每次插入都相當於在數組的第一個位置插入新的數據,所以需要移動大量的數據,所以最壞情況時間複雜度為O(n²)。
- 在數組中插入一個數據的平均時間複雜度是 O(n)。所以,對於插入排序來說,每次插入操作都相當於在數組中插入一個數據,循環執行n次插入操作,所以平均時間複雜度為O(n2)。
public static void insertionSort(int[] arr) {
int n = arr.length;
if (n <= 1) {
return;
}
for (int i = 0; i < n; i++) {
int value = arr[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j) {
if (arr[j] > value) {
arr[j + 1] = arr[j];//移動數據
} else {
break;
}
}
arr[j + 1] = value;//插入數據
}
}
四、選擇排序(Selection Sort)
- 選擇排序空間複雜度為 O(1),是一種原地排序演算法。
- 選擇排序的最好情況時間複雜度、最壞情況和平均情況時間複雜度都為O(n²)
- 選擇排序是一種不穩定的排序演算法,選擇排序每次都要找剩餘未排序元素中的最小值,並和前面的元素交換位置,這樣破壞了穩定性。
public static void selectionSort(int[] arr) {
int length = arr.length;
if (length == 1) {
return;
}
int x;
for (int i = 0; i < length; i++) {
x = i;
for (int j = i + 1; j < length; j++) {
if (arr[x] > arr[j]) {
x = j;
}
}
if(x != i){
int tmp = arr[i];
arr[i] = arr[x];
arr[x] = tmp;
}
}
}
總結一下
| 空間複雜度 | 是否穩定 | 最好時間複雜度 | 最壞時間複雜度 | 平均時間複雜度 | |
|---|---|---|---|---|---|
| 冒泡排序 | Q(1) | 是 | Q(n) | Q(n²) | Q(n²) |
| 插入排序 | Q(1) | 是 | Q(n) | Q(n²) | Q(n²) |
| 選擇排序 | Q(1) | 否 | Q(n²) | Q(n²) | Q(n²) |

