HashMap1.7和1.8,紅黑樹原理!
jdk 1.7
概述
HashMap基於Map介面實現,元素以鍵值對的方式存儲,並允許使用null鍵和null值,但只能有一個鍵作為null,因為key不允許重複,另外HashMap不能保證放入元素的數據,它是無序的,和放入的順序並不能相同,HashMap是執行緒不安全的。
繼承關係
public class HashMap<K,V>extends AbstractMap<K,V>
implements Map<K,V>, Cloneable, Serializable
基本屬性
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //默認初始化大小 16
static final float DEFAULT_LOAD_FACTOR = 0.75f; //負載因子0.75
static final Entry<?,?>[] EMPTY_TABLE = {}; //初始化的默認數組
transient int size; //HashMap中元素的數量
int threshold; //判斷是否需要調整HashMap的容量
HashMap的數據存儲結構
HashMap有數組和鏈表來實現對數據的存儲,HashMap採用Entry數組來存儲key-value對,每一個鍵值對組成了一個Entry實體,Entry類實際上是一個單向的鏈表結構,它具有Next指針,可以鏈接下一個Entry實體,以次來解決Hash衝突的問題。
數組存儲區間是連續的,佔用記憶體嚴重,故空間複雜的很大。但數組的二分查找時間複雜度小,為O(1);數組的特點是:定址容易,插入和刪除困難;
鏈表存儲區間離散,佔用記憶體比較寬鬆,故空間複雜度小,但時間複雜度很大,達 O(N) 。鏈表的特點是:定址困難,插入和刪除容易。
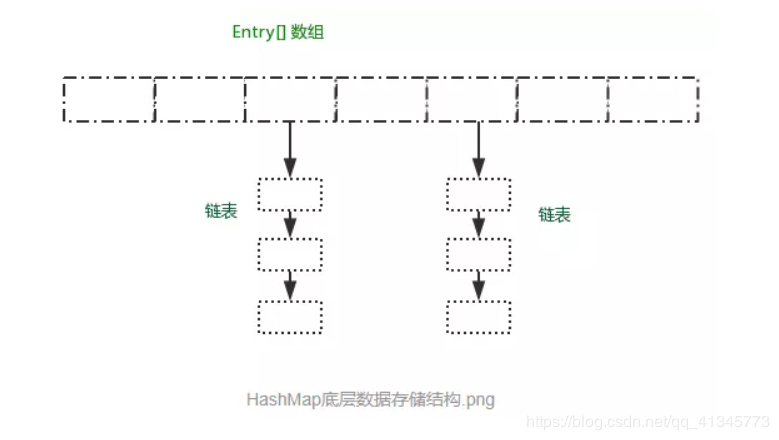
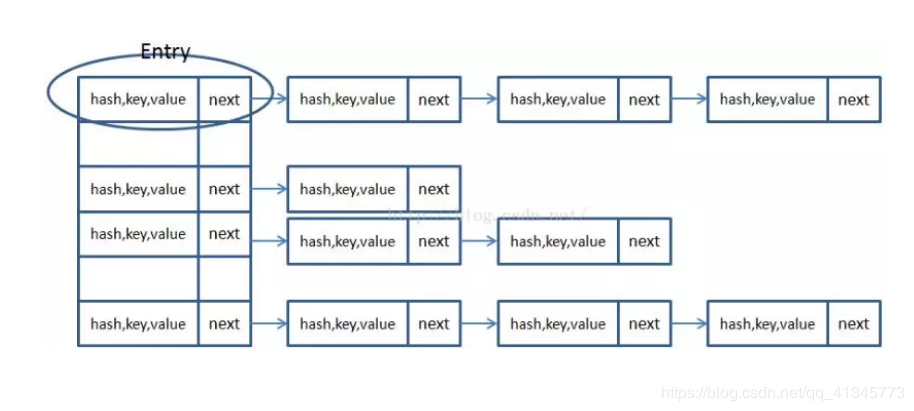
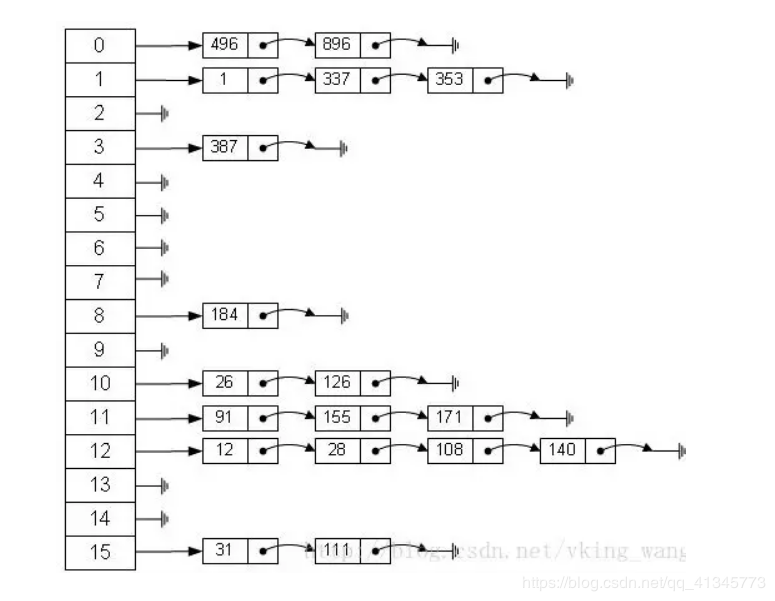
從上圖可以發現數組結構是由數組+鏈表組成,一個長度為16的數組中,每個元素存儲的是一個鏈表的頭節點。那麼這些元素是按照什麼樣的規矩存儲到數組中?
通過hash(key.hashCode())%length 獲得,也就是元素的key的哈希值對數組長度取模得到。比如上述哈希表中,12%16=12,28%16=12,108%16=12,140%16=12。所以12、28、108以及140都存儲在數組下標為12的位置。
取模運算的方式固然簡單,但是效率很低。為了實現高效的HashMao演算法,HashMap的發明者採用了位運算的方式。
公式: index = HashCode(Key) & (Length – 1)
以值為「book」的key來演示整個過程:
1.計算book的hashcode,結果為十進位的3029737,二進位的101110001110101110 1001。
2.假定HashMap長度是默認的16,計算Length-1的結果為十進位的15,二進位的1111。
3.把以上兩個結果做與運算,101110001110101110 1001 & 1111 = 1001,十進位是9,所以 index=9。
可以說,Hash演算法最終得到的index結果,完全取決於Key的Hashcode值的最後幾位。
這樣做不但效果上等同於取模,而且還大大提升了性能。
HashMap裡面實現一個靜態內部類Entry,其重要的屬性有 hash,key,value,next。
HashMap裡面用到鏈式數據結構的一個概念。上面我們提到過Entry類裡面有一個next屬性,作用是指向下一個Entry。打個比方, 第一個鍵值對A進來,通過計算其key的hash得到的index=0,記做:Entry[0] = A。一會後又進來一個鍵值對B,通過計算其index也等於0,現在怎麼辦?HashMap會這樣做:B.next = A,Entry[0] = B,如果又進來C,index也等於0,那麼C.next = B,Entry[0] = C;這樣我們發現index=0的地方其實存取了A,B,C三個鍵值對,他們通過next這個屬性鏈接在一起。
Put方法的原理
比如調用 hashMap.put(“apple”, 0) ,插入一個Key為「apple”的元素。這時候我們需要利用一個哈希函數來確定Entry的插入位置(index):
假定最後計算出的index是2,那麼結果如下:

但是,因為HashMap的長度是有限的,當插入的Entry越來越多時,再完美的Hash函數也難免會出現index衝突的情況。比如下面這樣:
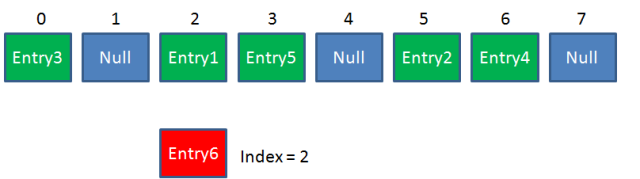
可以利用鏈表來解決。
HashMap數組的每一個元素不止是一個Entry對象,也是一個鏈表的頭節點。每一個Entry對象通過Next指針指向它的下一個Entry節點。當新來的Entry映射到衝突的數組位置時,只需要插入到對應的鏈表即可:
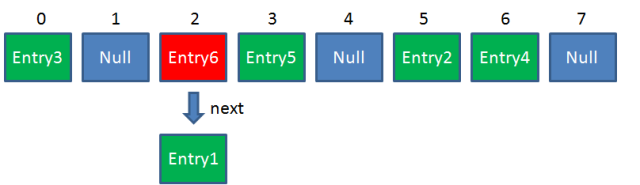
需要注意的是,新來的Entry節點插入鏈表時,使用的是「頭插法」。
Get方法的原理
首先會把輸入的Key做一次Hash映射,得到對應的index:
由於剛才所說的Hash衝突,同一個位置有可能匹配到多個Entry,這時候就需要順著對應鏈表的頭節點,一個一個向下來查找。假設我要查找的Key是「apple」:
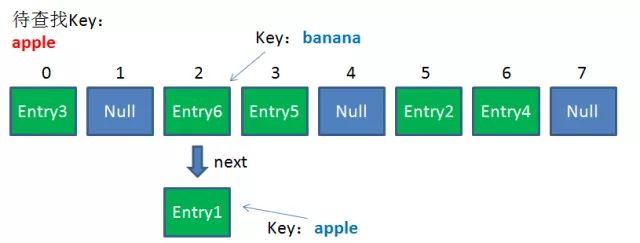
第一步,查看的是頭節點Entry6,Entry6的Key是banana,顯然不是我要找的結果。
第二步,查看的是Next節點Entry1,Entry1的Key是apple,正是我要找的結果。
之所以把Entry6放在頭節點,是因為HashMap的發明者認為,後插入的Entry被查找的可能性更大。
高並發下的HashMap
HashMap的容量是有限的。當經過多次元素插入,使得HashMap達到一定飽和度時,Key映射位置發生衝突的幾率會逐漸提高。
這時候,HashMap需要擴展它的長度,也就是進行Resize。
影響發生Resize的因素有兩個:
1.Capacity
HashMap的當前長度。HashMap的長度是2的冪。
2.LoadFactor
HashMap負載因子,默認值為0.75f。
衡量HashMap是否進行Resize的條件如下:
*HashMap.Size >= Capacity LoadFactor
HashMap的Rezie不是簡單的吧長度擴大,而是經過兩個步驟
1.擴容
創建一個新的Entry空數組,長度是原數組的2倍。
2.ReHash
遍歷原Entry數組,把所有的Entry重新Hash到新數組。為什麼要重新Hash呢?因為長度擴大以後,Hash的規則也隨之改變。
回顧一下Hash公式:
index = HashCode(Key) & (Length – 1)
當原數組長度為8時,Hash運算是和111B做與運算;新數組長度為16,Hash運算是和1111B做與運算。Hash結果顯然不同。
Resize前的HashMap:
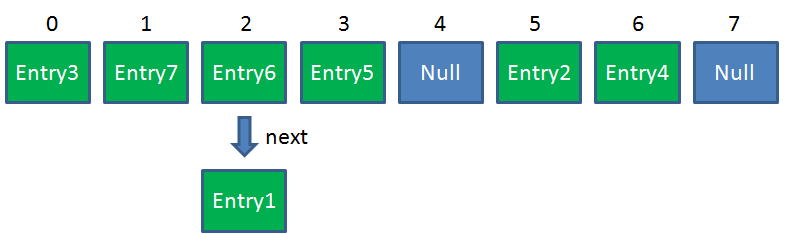
Resize後的HashMap:
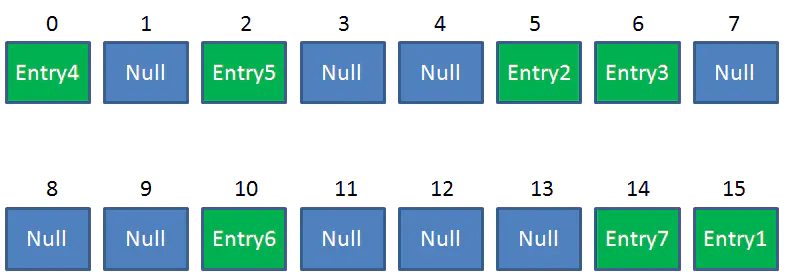
ReHash的Java程式碼如下:
/**
* Transfers all entries from current table to newTable.
*/
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
for (Entry<K,V> e : table) {
while(null != e) {
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}
單執行緒下執行沒有問題,多執行緒下的Rehash有問題!
假設一個HashMap已經到了Resize的臨界點。此時有兩個執行緒A和B,在同一時刻對HashMap進行Put操作:
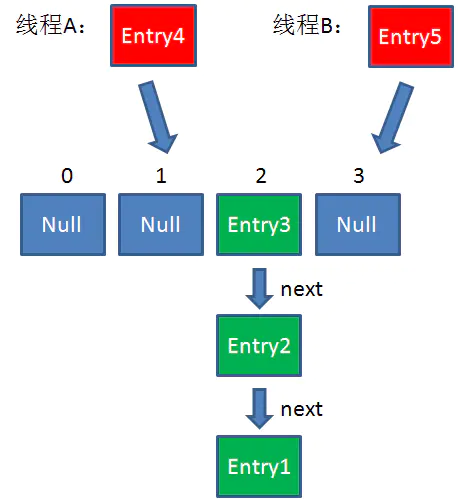
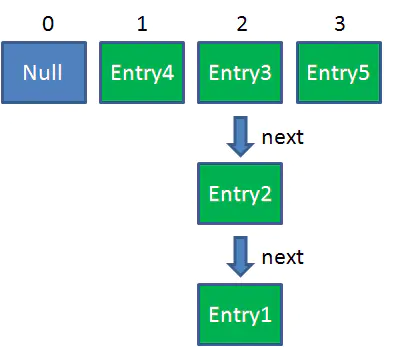
此時達到Resize條件,兩個執行緒各自進行Rezie的第一步,也就是擴容:
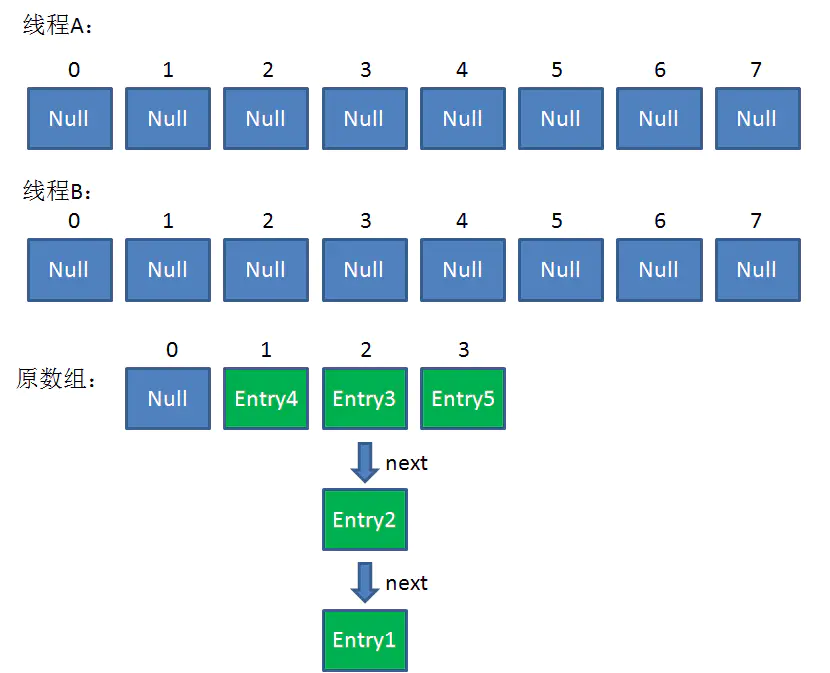
這時候,兩個執行緒都走到了ReHash的步驟。回顧一下ReHash的程式碼:

假如此時執行緒B遍歷到Entry3對象,剛執行完紅框里的這行程式碼,執行緒就被掛起。對於執行緒B來說:
e = Entry3
next = Entry2
這時候執行緒A暢通無阻地進行著Rehash,當ReHash完成後,結果如下(圖中的e和next,代表執行緒B的兩個引用):

直到這一步,看起來沒什麼毛病。接下來執行緒B恢復,繼續執行屬於它自己的ReHash。執行緒B剛才的狀態是:
e = Entry3
next = Entry2

當執行到上面這一行時,顯然 i = 3,因為剛才執行緒A對於Entry3的hash結果也是3。

我們繼續執行到這兩行,Entry3放入了執行緒B的數組下標為3的位置,並且e指向了Entry2。此時e和next的指向如下:
e = Entry2
next = Entry2
整體情況如圖所示:
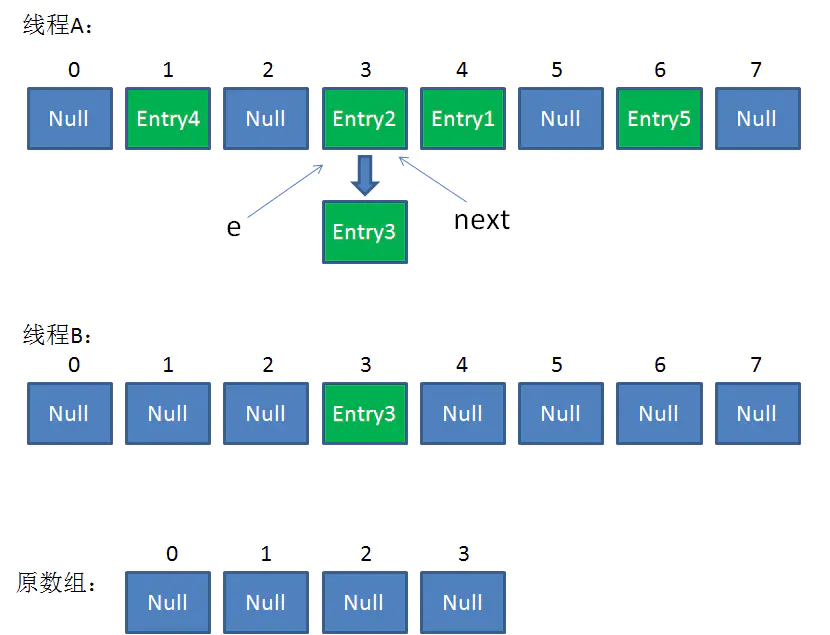
接著是新一輪循環,又執行到紅框內的程式碼行:

e = Entry2
next = Entry3
整體情況如圖所示:
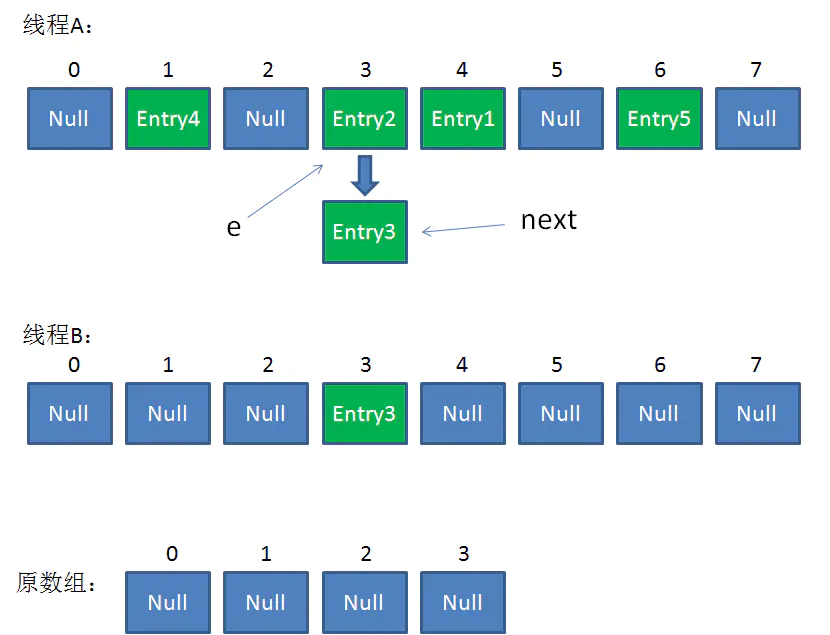
接下來執行下面的三行,用頭插法把Entry2插入到了執行緒B的數組的頭結點:

整體情況如圖所示:
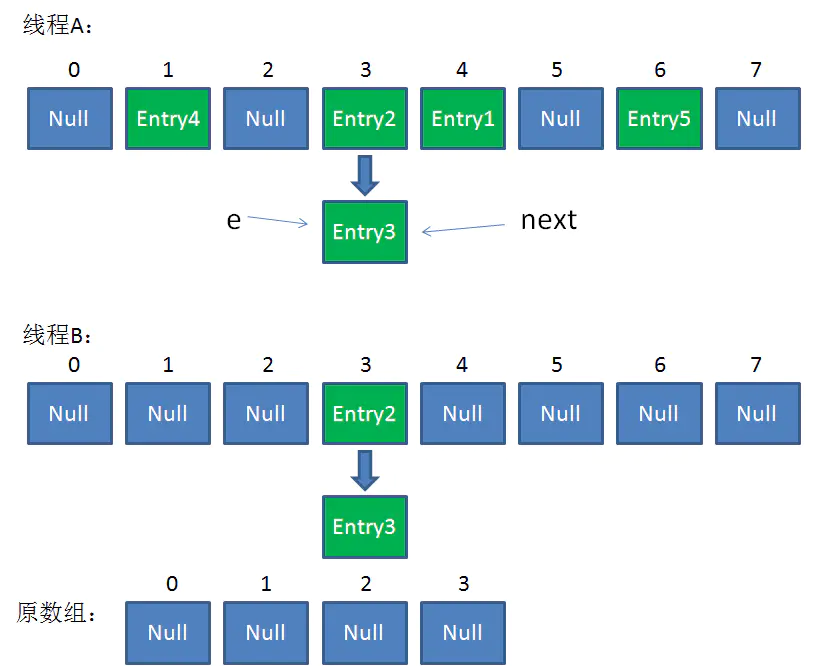
第三次循環開始,又執行到紅框的程式碼:

e = Entry3
next = Entry3.next = null
最後一步,當我們執行下面這一行的時候 !

newTable[i] = Entry2
e = Entry3
Entry2.next = Entry3
Entry3.next = Entry2
鏈表出現了環形!
整體情況如圖所示:
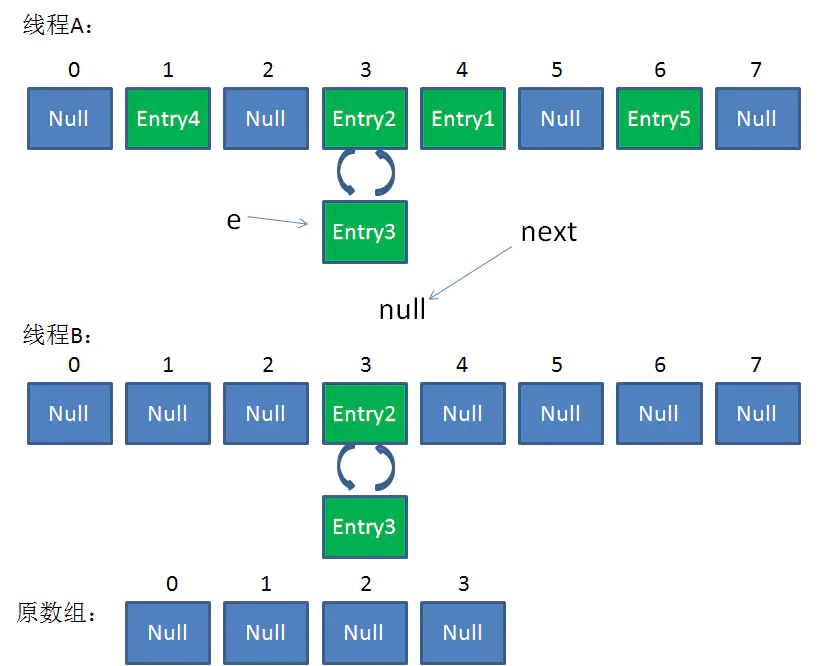
此時,問題還沒有直接產生。當調用Get查找一個不存在的Key,而這個Key的Hash結果恰好等於3的時候,由於位置3帶有環形鏈表,所以程式將會進入死循環!
在高並發下通常使用ConcurrentHashMap,這個集合類兼顧了執行緒安全和性能。
總結:
1.Hashmap在插入元素過多的時候需要進行Resize,Resize的條件是
HashMap.Size >= Capacity * LoadFactor。
2.Hashmap的Resize包含擴容和ReHash兩個步驟,ReHash在並發的情況下可能會形成鏈表環。
JDK 1.8
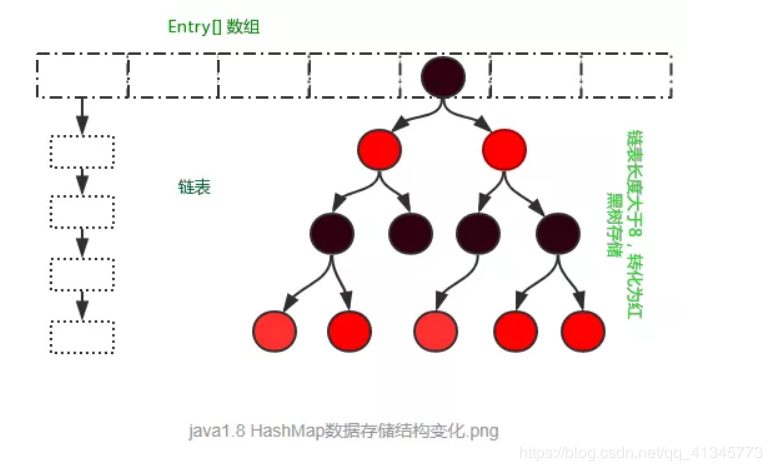
HashMap採用數組+鏈表+紅黑樹實現。
在Jdk1.8中HashMap的實現方式做了一些改變,但是基本思想還是沒有變得,只是在一些地方做了優化,數據結構的存儲由數組+鏈表的方式,變化為數組+鏈表+紅黑樹的存儲方式,當鏈表長度超過閾值(8)時,將鏈錶轉換為紅黑樹。在性能上進一步得到提升。
執行構造函數,當我們看到這個new,第一反應應該是在堆記憶體里開闢了一塊空間。
Map<String,Object> map = new HashMap<String,Object>();
構造方法:
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
初始化了一個負載因子
static final float DEFAULT_LOAD_FACTOR = 0.75f;
負載因子默認為0.75f
transient Node<K,V>[] table;
看到了數組,數組裡原對象是Node,來看下
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value; //key,value,用來存儲put的key,value值的
Node<K,V> next; // next ,用來標記下一個元素
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value; //構造函數
this.next = next;
}
put方法解析:
public V put(K key, V value) {
//調用putVal()方法完成
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//判斷table是否初始化,否則初始化操作
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//計算存儲的索引位置,如果沒有元素,直接賦值
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
//節點若已經存在,執行賦值操作
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
//判斷鏈表是否是紅黑樹
else if (p instanceof TreeNode)
//紅黑樹對象操作
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//為鏈表,
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
//鏈表長度8,將鏈錶轉化為紅黑樹存儲
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
//key存在,直接覆蓋
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
//記錄修改次數
++modCount;
//判斷是否需要擴容
if (++size > threshold)
resize();
//空操作
afterNodeInsertion(evict);
return null;
}
如果存在key節點,返回舊值,如果不存在則返回Null。

紅黑樹
首先需要理解二叉查找樹(Binary Search Tree)
二叉查找樹(BST)具備的特性
1.左子樹上所有結點的值均小於或等於它的根結點的值。
2.右子樹上所有結點的值均大於或等於它的根結點的值。
3.左、右子樹也分別為二叉排序樹。
下圖中這棵樹,就是一顆典型的二叉查找樹:
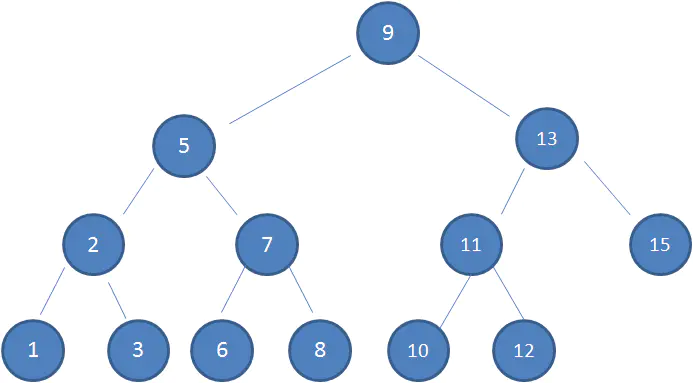
比如我要查找值為10的節點:
1、查看根節點9:
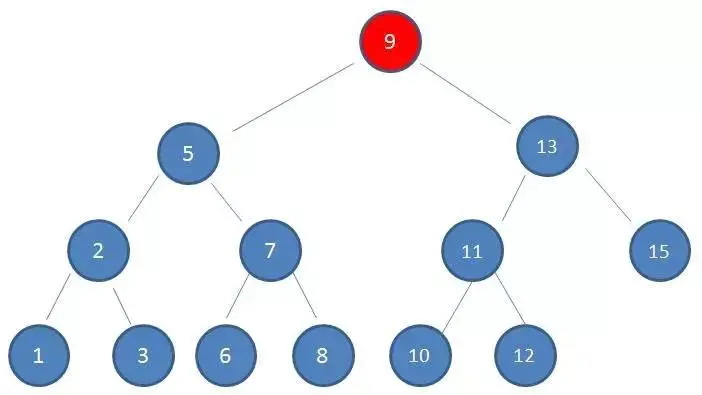
2、由於10 > 9,因此查看右孩子13:
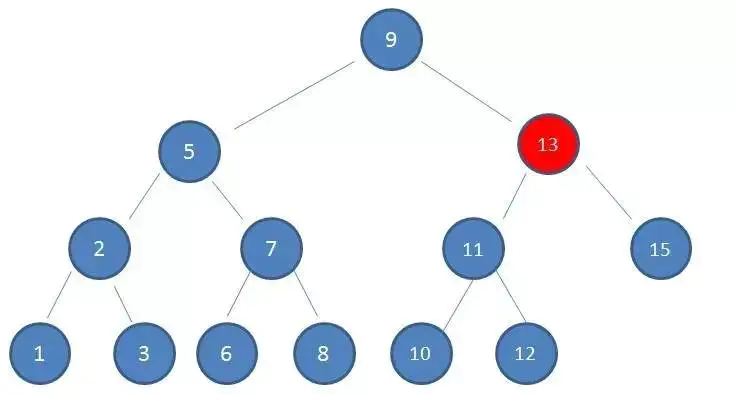
3、由於10 < 13,因此查看左孩子11:
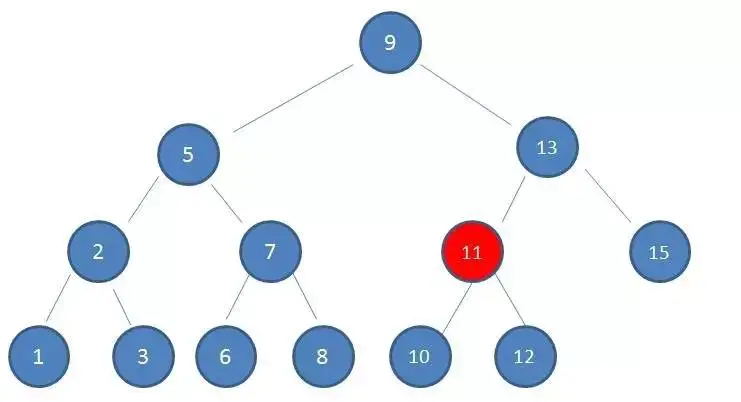
4.由於10 < 11,因此查看左孩子10,發現10正是要查找的節點:
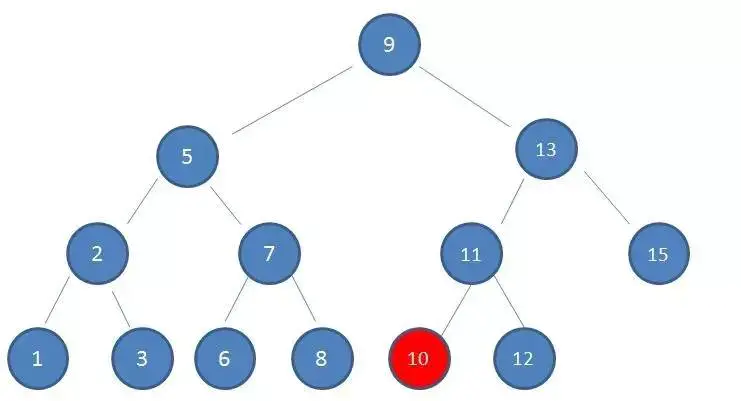
這種方式正是二分查找的思想,查找所需的最大次數等同於二叉查找樹的高度。
在插入節點的時候也是利用類似的方法,通過一層一層比較大小,找到新節點適合插入的位置。
但二叉查找樹存在缺陷,如:
假設初始的二叉查找樹只有三個節點,根節點值為9,左孩子值為8,右孩子值為12:
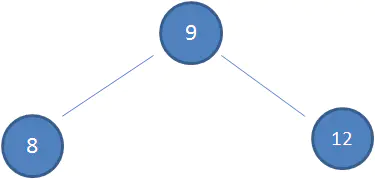
接下來我們依次插入如下五個節點:7,6,5,4,3。依照二叉查找樹的特性,結果會變成如下這樣:
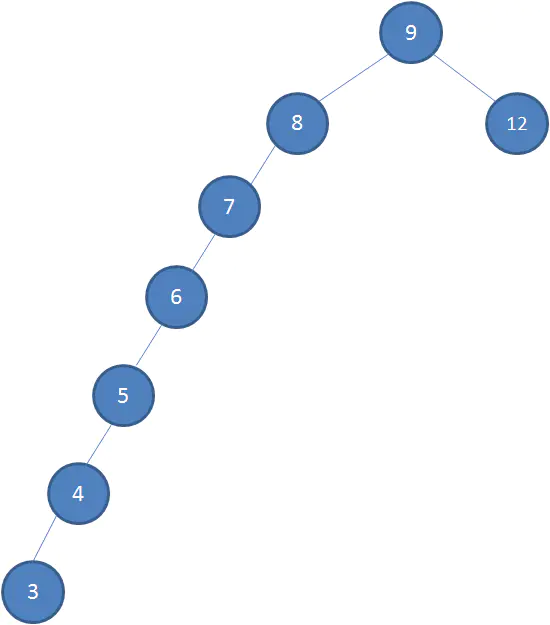
這樣的形態雖然也符合二叉查找樹的特性,但是查找的性能大打折扣,幾乎變成的線性。
如何解決二叉查找樹多次插入新節點而導致的不平衡?紅黑樹應運而生了。
紅黑樹(Red Black Tree) 是一種自平衡的二叉查找樹。除了符合二叉查找樹的基本特性外,它還具備下列的附加特性:
1、節點是紅色或黑色。
2、根節點是黑色。
3、每個葉子節點都是黑色的空節點(NIL節點)。
4 、每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
5、從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
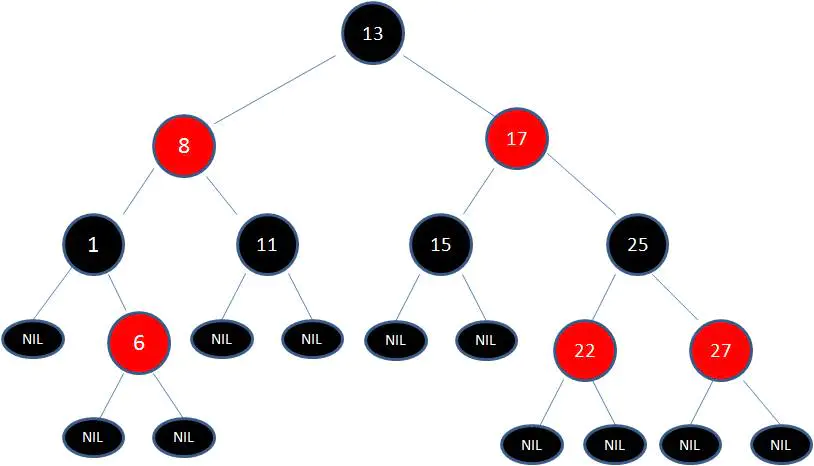
這張圖就是典型的紅黑樹!
正是因為這些規矩限制,才保證了紅黑樹的自平衡。紅黑樹從根到葉子的最長路徑不會超過最短路徑的2倍。
當插入或刪除節點的時候,紅黑樹的規則有可能被打破。這時候就需要做出一些調整,來繼續維持我們的規則。
什麼情況下會破壞紅黑樹的規則,什麼情況下不會破壞規則呢?舉兩個簡單的例子:
1、向原紅黑樹插入值為14的新節點:
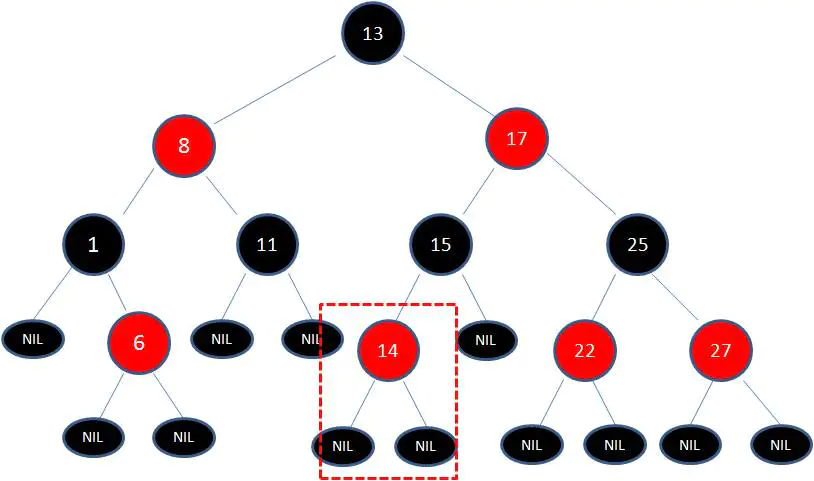
由於父節點15是黑色節點,因此這種情況並不會破壞紅黑樹的規則,無需做任何調整。
2、向原紅黑樹插入值為21的新節點:
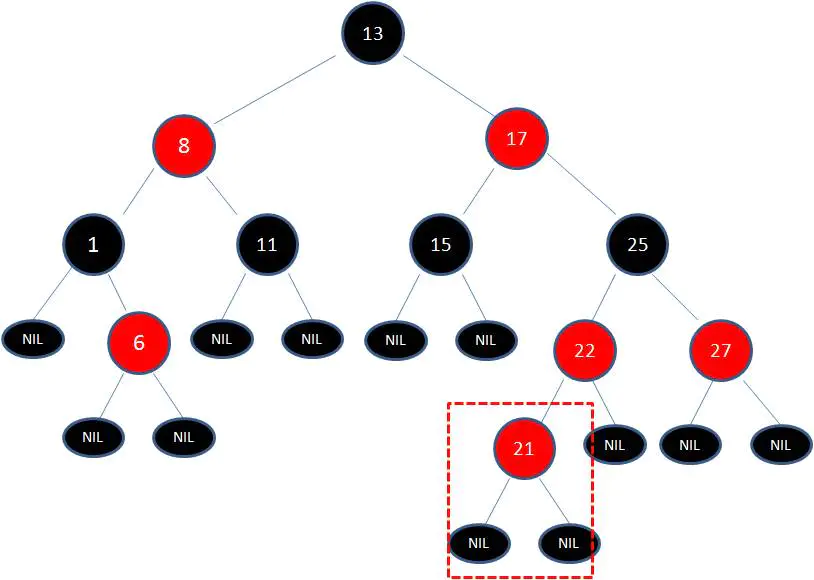
由於父節點22是紅色節點,因此這種情況打破了紅黑樹的規則4(每個紅色節點的兩個子節點都是黑色),必須進行調整,使之重新符合紅黑樹的規則。
調整有兩種方法:[變色]和[旋轉]。而旋轉又分成了兩種形式:[左旋轉]和[右旋轉]。
變色
為了重新符合紅黑樹的規則,嘗試把紅色節點變為黑色,或者把黑色節點變為紅色。
下圖所表示的是紅黑樹的一部分,需要注意節點25並非根節點。因為節點21和節點22連續出現了紅色,不符合規則4,所以把節點22從紅色變成黑色:
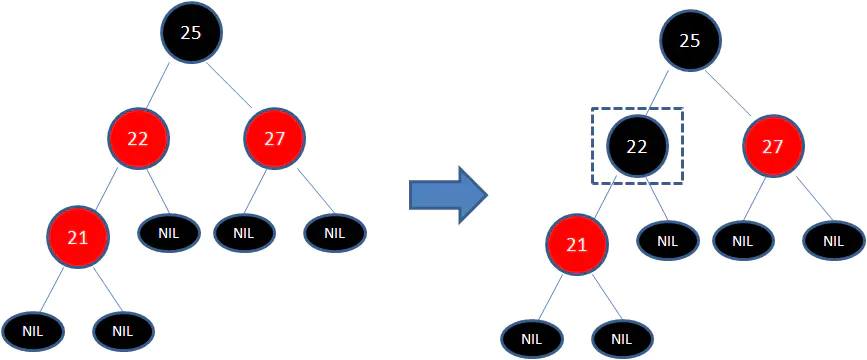
但這樣並不算完,因為憑空多出的黑色節點打破了規則5,所以發生連鎖反應,需要繼續把節點25從黑色變成紅色:
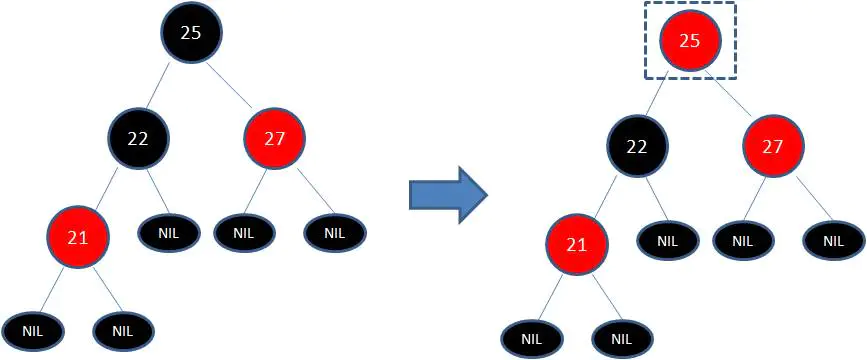
此時仍然沒有結束,因為節點25和節點27又形成了兩個連續的紅色節點,需要繼續把節點27從紅色變成黑色:
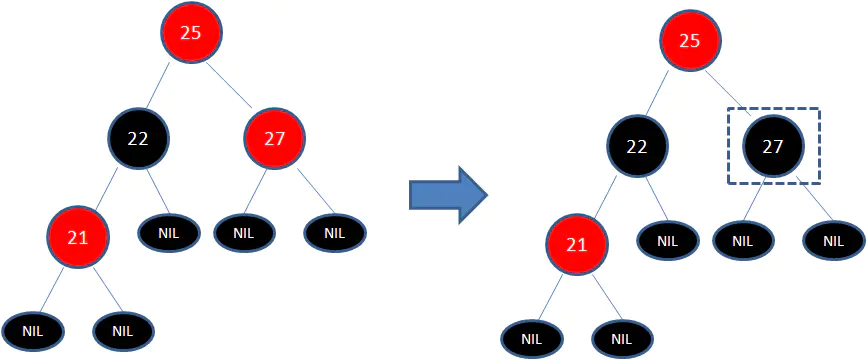
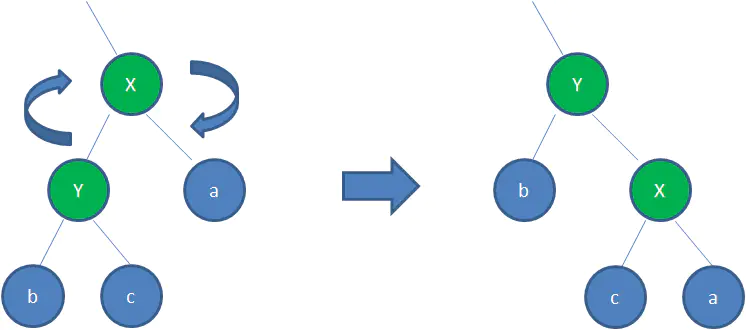
左旋轉:
逆時針旋轉紅黑樹的兩個節點,使得父節點被自己的右孩子取代,而自己成為自己的左孩子。看下圖:

圖中,身為右孩子的Y取代了X的位置,而X變成了自己的左孩子。此為左旋轉。
右旋轉:
順時針旋轉紅黑樹的兩個節點,使得父節點被自己的左孩子取代,而自己成為自己的右孩子。看下圖:
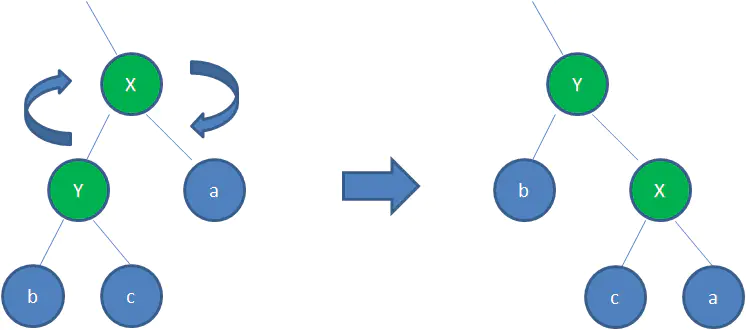
圖中,身為左孩子的Y取代了X的位置,而X變成了自己的右孩子。此為右旋轉。
紅黑樹的插入和刪除包含很多種情況,每一種情況都有不同的處理方式。在這裡舉個典型的例子,體會一下!
我們以剛才插入節點21的情況為例:
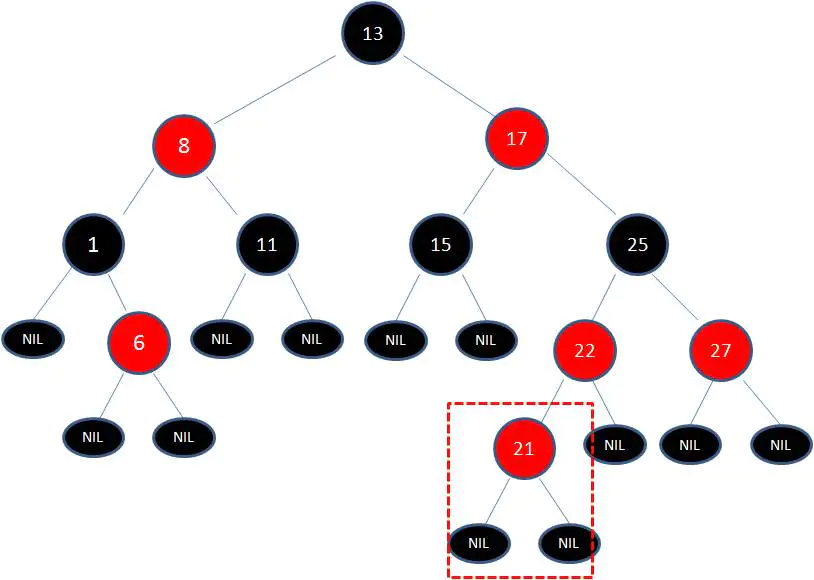
首先,我們需要做的是變色,把節點25及其下方的節點變色:
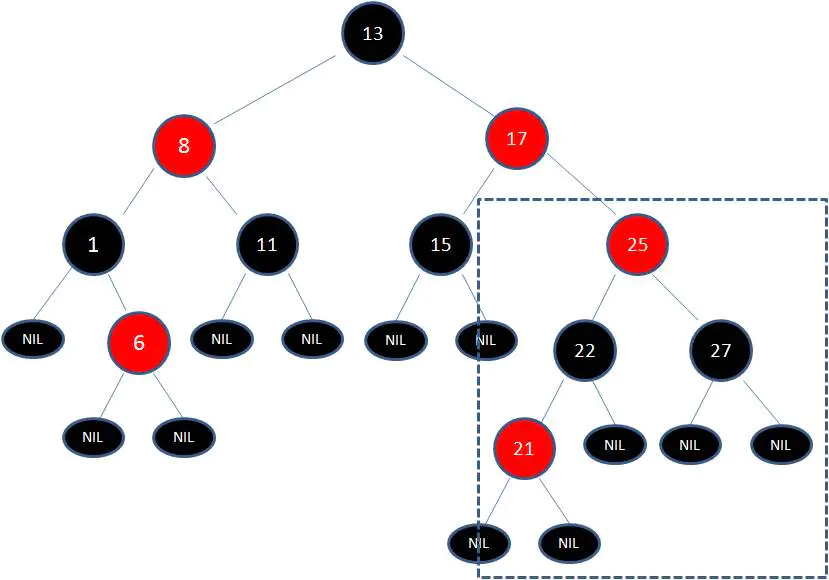
此時 節點17 和 節點25 是連續的兩個紅色節點,那麼把節點17變成黑色節點?恐怕不合適。這樣一來不但打破了規則4,而且根據規則2(根節點是黑色),也不可能把節點13變成紅色節點。
變色已無法解決問題,把節點13看著X,把節點17看著Y,想剛才的示意圖那樣進行左旋轉:

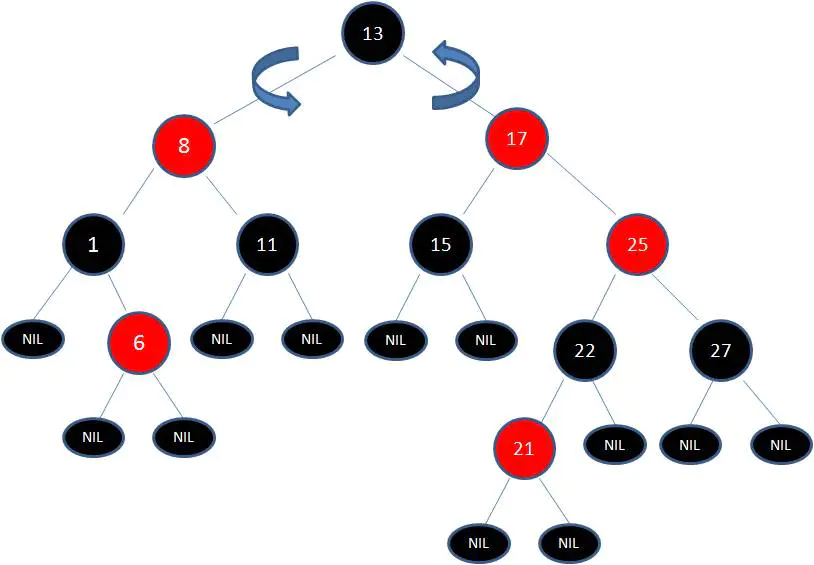
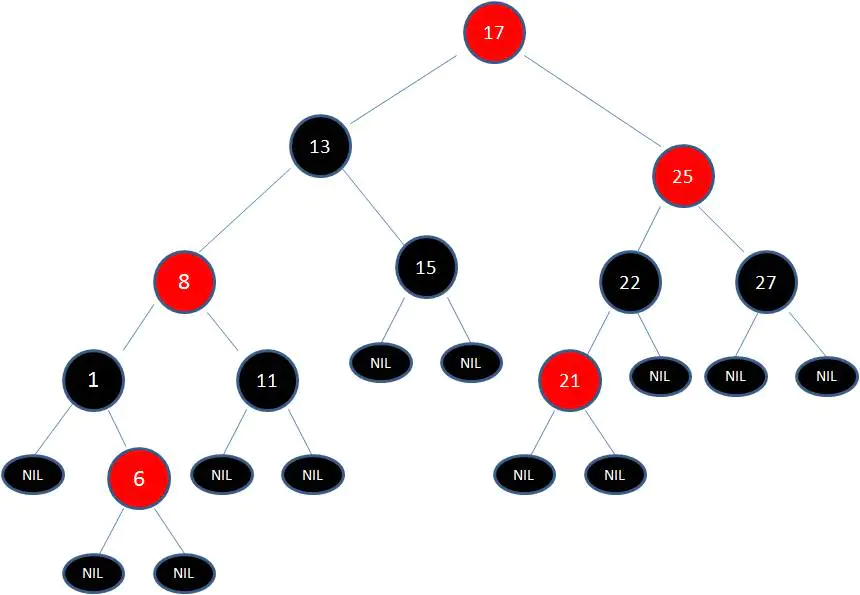
由於根節點必須是黑色節點,所以需要變色,變色結果如下:
這樣就結束了嗎?並沒有。因為其中兩條路徑(17 -> 8 -> 6 -> NIL)的黑色節點個數是4,其他路徑的黑色節點個數是3,不符合規則5。
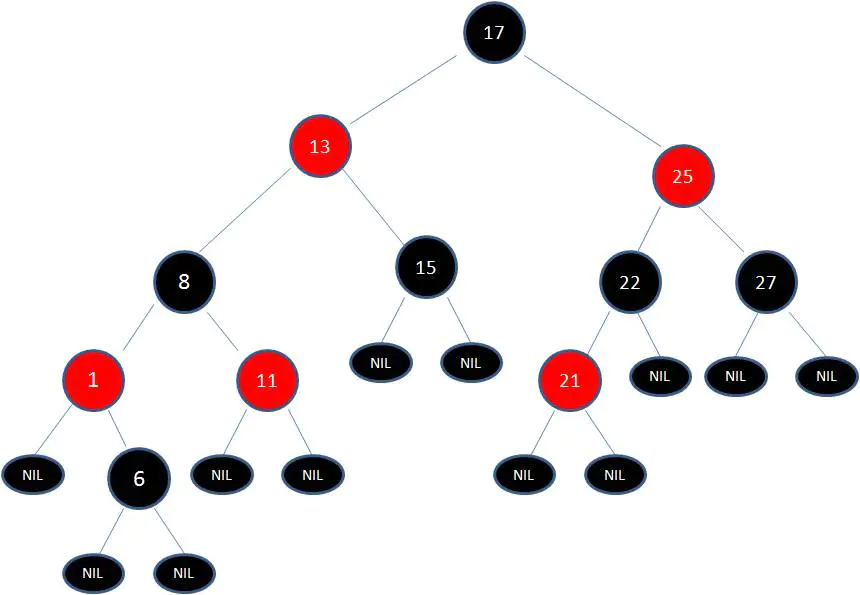
這時候我們需要把節點13看做X,節點8看做Y,像剛才的示意圖那樣進行右旋轉:
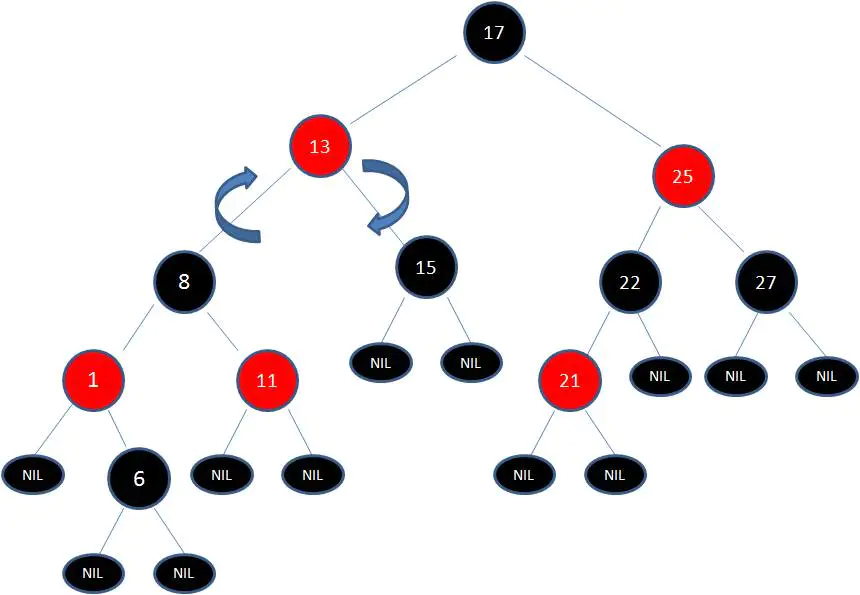
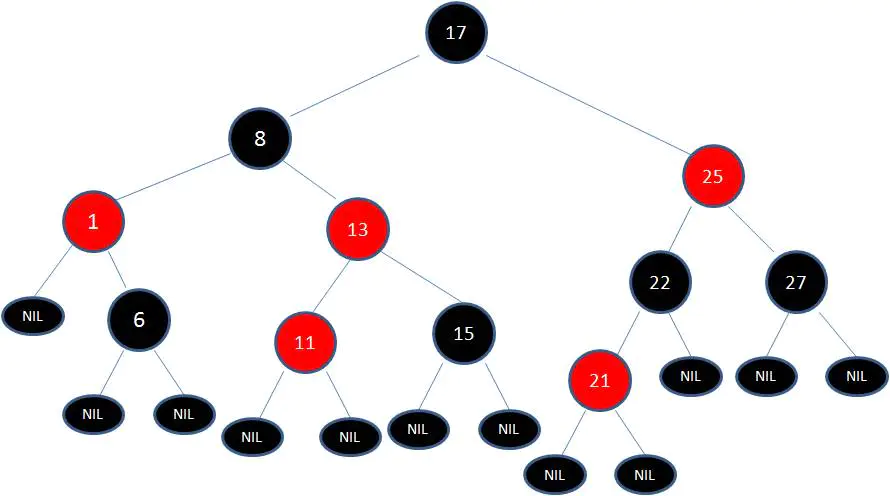
最後根據規則來進行變色:
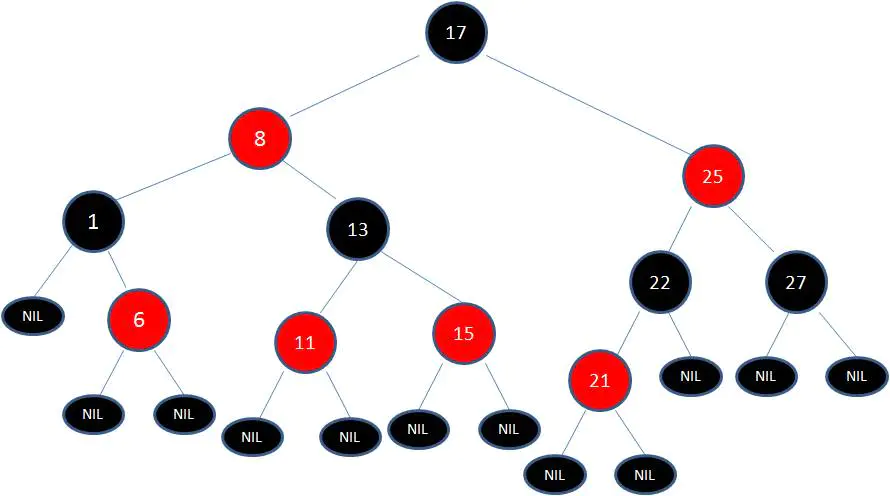
如此一來,紅黑樹變得重新符合規矩。 這一個例子的調整過程比較複雜,經歷了如下步驟: 變色 -> 左旋轉 -> 變色 -> 右旋轉 -> 變色
紅黑樹的應用有很多,除了HashMap,jdk 的集合類TreeMap和TreeSet 底層就是紅黑樹實現的。
幾點說明:
1、關於紅黑樹自平衡的調整,插入和刪除節點的時候都涉及到很多種Case,由於篇幅原因無法展開來一一列舉,有興趣的朋友可以參考維基百科,裡面講的非常清晰。
2、紅黑樹調整過程的示例是一種比較複雜的情形,沒太看明白的小夥伴也不必鑽牛角尖,關鍵要懂得紅黑樹自平衡調整的主體思想。
參考文章
//juejin.im/post/5a27c6946fb9a04509096248
//zhuanlan.zhihu.com/p/28501879
//blog.csdn.net/qq_41345773/article/details/92066554


