前端演算法渣的救贖之路🚀

2020 年 5 月 31 日
筆記
數據結構與演算法

前言

dp

思想

感覺很像時高中數列的思想，給出首項，以及一個遞推式子，讓你求任意項的值。

步驟基本是：尋找狀態轉移方程 => 建立合適的數據結構表 => 填表

爬樓梯

假設你正在爬樓梯。需要 n 階你才能到達樓頂。

每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢

dp[0] = 0 dp[1] = 1 dp[2] = 2
dp[n] = dp[n-1] + dp[n-2]   // 到達第n階樓梯有從n-1階走一步和從第n-2階走兩步兩種情況
var climbStairs = function(n) {
    let dp = [];
    dp[0] = 0,dp[1] = 1,dp[2] = 2;
    for(let i = 3;i <= n;i++){
        dp[i] = dp[i-2] + dp[i-1];
    }
    return dp[n];
};

打家劫舍

你是一個專業的小偷，計劃偷竊沿街的房屋。每間房內都藏有一定的現金，影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警。

給定一個代表每個房屋存放金額的非負整數數組，計算你在不觸動警報裝置的情況下，能夠偷竊到的最高金額

// 動態規劃方程：dp[n] = MAX( dp[n-1], dp[n-2] + num )
// 由於不可以在相鄰的房屋闖入，所以在當前位置 n 房屋可盜竊的最大值，要麼就是 n-1 房屋可盜竊的最大值，要麼就是 n-2 房屋可盜竊的最大值加上當前房屋的值，二者之間取最大值
// 舉例來說：1 號房間可盜竊最大值為 33 即為 dp[1]=3，2 號房間可盜竊最大值為 44 即為 dp[2]=4，3 號房間自身的值為 22 即為 num=2，那麼 dp[3] = MAX( dp[2], dp[1] + num ) = MAX(4, 3+2) = 5，3 號房間可盜竊最大值為 55

var rob = function(nums) {
    if(nums.length === 0) return 0;
    if(nums.length === 1) return nums[0];
    if(nums.length === 2) return Math.max(nums[0],nums[1]);
    if(nums.length === 3) return Math.max(nums[0] + nums[2],nums[1]);
    let dp = [nums[0],nums[1],Math.max(nums[0] + nums[2],nums[1])];
    for(let i = 3;i < nums.length;i++){
        dp[i] = nums[i] + Math.max(dp[i-2],dp[i-3]);
    }
    return Math.max(dp[nums.length-1],dp[nums.length-2]);
};

最大正方形

在一個由 0 和 1 組成的二維矩陣內，找到只包含 1 的最大正方形，並返回其面積

const maximalSquare = (matrix) => {
  if (!matrix.length) return 0
  
  let maxsqlen = 0
  let rowLength = matrix.length, colLength = matrix[0].length
  for (let row = 0; row < rowLength; row++) {
    for (let col = 0; col < colLength; col++) {
      if (matrix[row][col] === '1') {
        matrix[row][col] = Number(matrix[row][col])
        if (row != 0 && col != 0) {
          matrix[row][col] = Math.min(matrix[row-1][col], matrix[row-1][col-1], matrix[row][col-1]) + 1
        }
        maxsqlen = Math.max(maxsqlen, matrix[row][col])
      } 
    }
  }
  return maxsqlen**2 
    
}

/** DP 
 * 題目要求最大正方形面積，面積 = 邊長 * 邊長，也就是求最大正方形的邊長
 * 所以也就變成了，在矩陣中找最大正方形，矩陣中只有0｜1兩種值，全部為1的才是正方形
 * 如何知道矩陣中哪裡是1，哪裡是0，只能窮舉，但要聰明的窮舉，這不就是動態規劃的本質嘛！
 * 動態規劃第一步，先假象我們創建了一個二維數組dp，用來存儲「這個點為右下角的最大正方形的邊長」
 * 下面開始找 狀態轉換方程
 * 思路：假設有如下矩陣
 * 1 0 1 1 1
 * 1 1 1 1 1
 * 1 1 1 1 1
 * 1 0 0 1 1
 * 隨便找一個點，直觀地，我們先找最右下角的點，設該點的最大正方形邊長為 dp[i][j], 我們用肉眼看一下，dp[i][j] 應該等於 2
 * 為什麼等於2，是因為我們看了 dp[i-1][j], dp[i-1][j-1], dp[i][j-1] 這三個點都為1，而又因為dp[i][j-2] 為0，所以
 * 我們知道dp[i][j]最大就為2了。也就是我們不能只看dp[i][j]相鄰的三個點，而應該看「這三個相鄰點為正方形右下角」的邊長情況，
 * 取最小邊長進行求解 dp[i][j] 的最大正方形邊長。（看，我們找到了重疊子問題和最優子結構）
 * 所以，狀態轉換方程為：dp[i][j] = Math.min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1
 * 下一步，需要根據矩陣數據，進行選擇和明確 base case 即可
 */

零錢兌換

給定不同面額的硬幣 coins 和一個總金額 amount。編寫一個函數來計算可以湊成總金額所需的最少的硬幣個數。如果沒有任何一種硬幣組合能組成總金額，返回 -1

var coinChange = function(coins, amount) {
  let dp = new Array( amount + 1 ).fill( Infinity );
  dp[0] = 0;
  
  for (let i = 1; i <= amount; i++) {
    for (let coin of coins) {
      if (i - coin >= 0) {
        dp[i] = Math.min(dp[i], dp[i - coin] + 1);
      }
    }
  }
  
  return dp[amount] === Infinity ? -1 : dp[amount];
}

不同路徑

一個機器人位於一個 m x n 網格的左上角（起始點在下圖中標記為「Start」）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為「Finish」）。

問總共有多少條不同的路徑

var uniquePaths = function(m, n) {
    if(m === 1 && n === 1) return 1;
    let data = [],rows = [0];
    for(let i = 0;i < n-1;i++){
        rows.push(1);
    }
    data.push(rows);
    for(let i = 0;i < m-1;i++){
        data.push([1]);
    }
    for(let i = 1;i < m;i++){
        for(let j = 1;j < n;j++){
            data[i][j] = data[i-1][j] + data[i][j-1];
        }
    }
    return data[m-1][n-1];
};

股票題狀態機

本文就來告訴你這個框架，然後帶著你一道一道秒殺。

這 6 道股票買賣問題是有共性的，我們通過對第四題（限制最大交易次數為 k）的分析一道一道解決。因為第四題是一個最泛化的形式，其他的問題都是這個形式的簡化。

第一題是只進行一次交易，相當於 k = 1；第二題是不限交易次數，相當於 k = +infinity（正無窮）；第三題是只進行 2 次交易，相當於 k = 2；剩下兩道也是不限次數，但是加了交易「冷凍期」和「手續費」的額外條件，其實就是第二題的變種，都很容易處理。

一、窮舉框架

首先，還是一樣的思路：如何窮舉？這裡的窮舉思路和上篇文章遞歸的思想不太一樣。

遞歸其實是符合我們思考的邏輯的，一步步推進，遇到無法解決的就丟給遞歸，一不小心就做出來了，可讀性還很好。缺點就是一旦出錯，你也不容易找到錯誤出現的原因。比如上篇文章的遞歸解法，肯定還有計算冗餘，但確實不容易找到。

而這裡，我們不用遞歸思想進行窮舉，而是利用「狀態」進行窮舉。我們具體到每一天，看看總共有幾種可能的「狀態」，再找出每個「狀態」對應的「選擇」。我們要窮舉所有「狀態」，窮舉的目的是根據對應的「選擇」更新狀態。聽起來抽象，你只要記住「狀態」和「選擇」兩個詞就行，下面實操一下就很容易明白了。

for 狀態1 in 狀態1的所有取值：
    for 狀態2 in 狀態2的所有取值：
        for ...
            dp[狀態1][狀態2][...] = 擇優(選擇1，選擇2...)

比如說這個問題，每天都有三種「選擇」：買入、賣出、無操作，我們用 buy, sell, rest 表示這三種選擇。但問題是，並不是每天都可以任意選擇這三種選擇的，因為 sell 必須在 buy 之後，buy 必須在 sell 之後。那麼 rest 操作還應該分兩種狀態，一種是 buy 之後的 rest（持有了股票），一種是 sell 之後的 rest（沒有持有股票）。而且別忘了，我們還有交易次數 k 的限制，就是說你 buy 還只能在 k > 0 的前提下操作。

很複雜對吧，不要怕，我們現在的目的只是窮舉，你有再多的狀態，老夫要做的就是一把梭全部列舉出來。這個問題的「狀態」有三個，第一個是天數，第二個是允許交易的最大次數，第三個是當前的持有狀態（即之前說的 rest 的狀態，我們不妨用 1 表示持有，0 表示沒有持有）。然後我們用一個三維數組就可以裝下這幾種狀態的全部組合：

dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 為天數，大 K 為最多交易數
此問題共 n × K × 2 種狀態，全部窮舉就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

而且我們可以用自然語言描述出每一個狀態的含義，比如說 dp[3][2][1] 的含義就是：今天是第三天，我現在手上持有著股票，至今最多進行 2 次交易。再比如 dp[2][3][0] 的含義：今天是第二天，我現在手上沒有持有股票，至今最多進行 3 次交易。很容易理解，對吧？

我們想求的最終答案是 dp[n – 1][K][0]，即最後一天，最多允許 K 次交易，最多獲得多少利潤。讀者可能問為什麼不是 dp[n – 1][K][1]？因為 [1] 代表手上還持有股票，[0] 表示手上的股票已經賣出去了，很顯然後者得到的利潤一定大於前者。

記住如何解釋「狀態」，一旦你覺得哪裡不好理解，把它翻譯成自然語言就容易理解了。

二、狀態轉移框架

現在，我們完成了「狀態」的窮舉，我們開始思考每種「狀態」有哪些「選擇」，應該如何更新「狀態」。只看「持有狀態」，可以畫個狀態轉移圖。

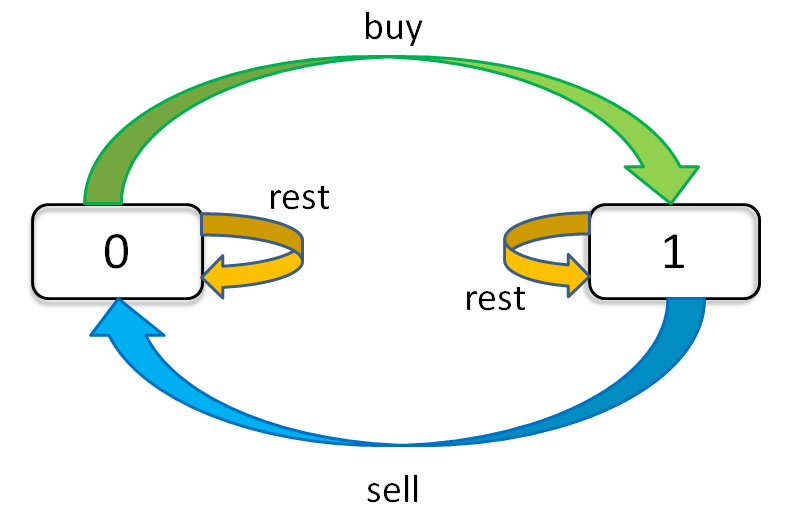
通過這個圖可以很清楚地看到，每種狀態（0 和 1）是如何轉移而來的。根據這個圖，我們來寫一下狀態轉移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max(   選擇 rest  ,           選擇 sell      )

解釋：今天我沒有持有股票，有兩種可能：
要麼是我昨天就沒有持有，然後今天選擇 rest，所以我今天還是沒有持有；
要麼是我昨天持有股票，但是今天我 sell 了，所以我今天沒有持有股票了。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max(   選擇 rest  ,           選擇 buy         )

解釋：今天我持有著股票，有兩種可能：
要麼我昨天就持有著股票，然後今天選擇 rest，所以我今天還持有著股票；
要麼我昨天本沒有持有，但今天我選擇 buy，所以今天我就持有股票了。

這個解釋應該很清楚了，如果 buy，就要從利潤中減去 prices[i]，如果 sell，就要給利潤增加 prices[i]。今天的最大利潤就是這兩種可能選擇中較大的那個。而且注意 k 的限制，我們在選擇 buy 的時候，把 k 減小了 1，很好理解吧，當然你也可以在 sell 的時候減 1，一樣的。

現在，我們已經完成了動態規劃中最困難的一步：狀態轉移方程。如果之前的內容你都可以理解，那麼你已經可以秒殺所有問題了，只要套這個框架就行了。不過還差最後一點點，就是定義 base case，即最簡單的情況。

如果你最多只允許完成一筆交易（即買入和賣出一支股票一次），設計一個演算法來計算你所能獲取的最大利潤。

var maxProfit = function(prices) {
    let dp_i_0 = 0,dp_i_1 = -Infinity;
    for(let i = 0;i < prices.length;i++){
        dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
        dp_i_1 = Math.max(dp_i_1,-prices[i]);
    }
    return dp_i_0;
};

買賣股票的最佳時機 II

1. 只要股票價格上漲，上漲的部分就是我的利潤，可以理解為上漲期間第一天買入，然後一直持有到上漲最後一天即下跌前一天再賣出
2. 只要股票價格下跌，那我肯定在下跌前一天賣了，而且下跌期間永遠不會買入
var maxProfit = function(prices) {
  let profit = 0;
  for (let i = 0; i < prices.length - 1; i++) {
    if (prices[i + 1] > prices[i]) profit += prices[i + 1] - prices[i];
  }
  return profit;
};

貪心

思想

在對問題求解時，總是做出在當前看來是最好的選擇。也就是說，不從整體最優上加以考慮，他所做出的是在某種意義上的局部最優解最優解

給你一根長度為 n 的繩子，請把繩子剪成整數長度的 m 段（m、n都是整數，n>1並且m>1），每段繩子的長度記為 k[0],k[1]…k[m] 。請問 k[0]k[1]…*k[m] 可能的最大乘積是多少？例如，當繩子的長度是8時，我們把它剪成長度分別為2、3、3的三段，此時得到的最大乘積是18。

剪繩子

var cuttingRope = function(number) {
    if(number === 2 || number === 3) return number - 1;
    let a = number % 3;
    let b = parseInt(number / 3);
    if(a === 0){
        return 3 ** b;
    }else if(a === 1){
        return 2 * 2 * (3 ** (b - 1));
    }else{
        return 2 * (3 ** b);
    }
};

跳躍遊戲

給定一個非負整數數組，你最初位於數組的第一個位置。

數組中的每個元素代表你在該位置可以跳躍的最大長度。

判斷你是否能夠到達最後一個位置。

1. 使用一個變數保存當前可到達的最大位置
2. 時刻更新最大位置
3. 可達位置小於數組長度返回false，反之即反
var canJump = function(nums) {
    let k = 0;
    for(let i = 0;i < nums.length;i++){
        if(i > k) return false;
        k = Math.max(k,i + nums[i]);
    }
    return true;
};

加油站

在一條環路上有 N 個加油站，其中第 i 個加油站有汽油 gas[i] 升。

你有一輛油箱容量無限的的汽車，從第 i 個加油站開往第 i+1 個加油站需要消耗汽油 cost[i] 升。你從其中的一個加油站出發，開始時油箱為空。

如果你可以繞環路行駛一周，則返回出發時加油站的編號，否則返回 -1

1. gas - cost >= 0才能繞場一周，以此思想判斷能否行駛一周
2. 從正確初始位置開始，擁有的汽油總是比消耗的汽油多,以此思想尋找初始位置
var canCompleteCircuit = function(gas, cost) {
    let cur = 0,total = 0,start = 0;
    for(let i = 0;i < gas.length;i++){
        total += gas[i] - cost[i];
        if(cur < 0){
            cur = gas[i] - cost[i];
            start = i;
        }else cur += gas[i] - cost[i];
    }
    return total >= 0 ? start : -1;
};

二分

思想

針對有序數列進行查找時，優先考慮二分

輸入一個非遞減排序的數組的一個旋轉，輸出旋轉數組的最小元素

// 例如數組{3,4,5,1,2}為{1,2,3,4,5}的一個旋轉，該數組的最小值為1。
// NOTE：給出的所有元素都大於0，若數組大小為0，請返回0。
//把一個數組最開始的若干個元素搬到數組的末尾，我們稱之為數組的旋轉。
//10111

1. 原數據為旋轉數組，所以分界點前後都是有序的
2. 進行二分查找，注意因為找最小值，high賦值時應該從mid開始取，mid可能是最小值
function minNumberInRotateArray(rotateArray)
{
    if(!rotateArray.length) return 0;
    let left = 0,right = rotateArray.length-1;
    while(left < right){
        let mid = Math.floor((right+left) >> 1);
        if(rotateArray[left] <= rotateArray[right]){
            return rotateArray[left];
        }
        if(rotateArray[left] < rotateArray[mid]){
            left = mid + 1;
        }else if(rotateArray[right] > rotateArray[mid]){
            right = mid;
        }else{
            left++;
        }
    }
}

統計一個數字在排序數組中出現的次數

function GetNumberOfK(data, k)
{
    let low = 0,high = data.length-1;
    let pos,count = 0;
    while(low < high){
        let mid = Math.floor((low+high)>>1);
        if(data[mid] === k){
            pos = mid;
            break;
        }else if(data[mid] < k){
            low = mid + 1;
        }else{
            high = mid-1;
        }
    }
    if(pos !== undefined){
        count++;
        let left = pos,right = pos;
        while(left--){
            if(data[left] === k){
                count++;
            }else{
                break;
            }
        }
        while(right++){
            if(data[right] === k){
                count++;
            }else{
                break;
            }
        }
        return count;
    }else return 0;
}

0～n-1中缺失的數字

一個長度為n-1的遞增排序數組中的所有數字都是唯一的，並且每個數字都在範圍0～n-1之內。在範圍0～n-1內的n個數字中有且只有一個數字不在該數組中，請找出這個數字

var missingNumber = function(nums) {
    let left = 0,
        right = nums.length - 1;
    while (left <= right) {
        let mid = Math.floor((left + right) / 2);
        if (mid === nums[mid]) {
            left = mid + 1;
        } else if (mid < nums[mid]) {
            right = mid - 1;
        }
    }
    return left;
};

最長上升子序列

1. 維護一個子序列存放當前的上升序列
2. 將當前數與子序列最大值比較，如果比最大值大之間加入隊尾，如果更新則找一個合適的位置替換當前位置的元素
var lengthOfLIS = function(nums) {
    let n = nums.length;
    if(n <= 1){
        return n;
    }
    let tail = [nums[0]];
    for(let i = 0;i < n;i++){
        if(nums[i] > tail[tail.length-1]){
            tail.push(nums[i]);
        }else{
            let left = 0;
            let right = tail.length-1;
            while(left < right){
                let mid = (left + right) >> 1;
                if(tail[mid] < nums[i]){
                    left = mid + 1;
                }else{
                    right = mid;
                }
            }
            tail[left] = nums[i];
        }
    }
    return tail.length;
};

搜索二維矩陣 II

編寫一個高效的演算法來搜索 m x n 矩陣 matrix 中的一個目標值 target。該矩陣具有以下特性：

每行的元素從左到右升序排列。
每列的元素從上到下升序排列。

輸入這樣的一個二維數組和一個整數，判斷數組中是否含有該整數。
1. 選取左下角的值作為初始值key
2. 如果目標值大於key，因為是最左邊的值（最小），所以col++
3. 如果目標值小於，那麼更小的值只可能是上一行，所以row--
function Find(target,array){
    let rows = array.length;
    if(rows <= 0) return false;
    let cols = array[0].length;
    if(cols <= 0) return false;
    let row = rows - 1;
    let col = 0;
    while(row >= 0 && col < cols){
        if(array[row][col] > target){
            row--;
        }else if(array[row][col] < target){
            col++;
        }else{
            return true;
        }
    }
    return false;
}

Pow(x, n)

實現 pow(x, n) ，即計算 x 的 n 次冪函數

//快速冪演算法
var myPow = function(x, n) {
    if (!x) return 0;
    if (x === 1) return 1;
    if (x === -1) return (n & 1) ? -1 : 1;
    if (n == 2147483647) return 0;
    if (n == -2147483648) return x === 2 ? 0 : 1;
    if (n < 0) {
        x = 1 / x;
        n = -n;
    }
    let res = 1;
    while(n) {
        if (n & 1) res *= x;
        x *= x;
        n >>= 1;
    }
    return res;
}

求交集

function intersection(...args){
	if(!args.length) return [];
    let res = [],left = args[0][0],right = args[0][1];
    for(let i = 1;i < args.length;i++){
       if(right >= args[i][0] || left <= args[i][1]){
         left = Math.max(left,args[i][0]);
         right = Math.min(right,args[i][1]);
         res = [left,right];
       }else{
        return [];
       }
     }
   return res;
}

回溯演算法

解題思路

全局變數：保存結果
參數：遞歸函數的參數選擇，通常是兩種參數。
- 狀態變數： result需要保存的值
- 條件變數：判斷搜索是否完畢以及搜索是否合法
完成條件：完成條件是決定狀態變數和條件變數取何值時可以判斷整個搜索流程結束。整個搜索流程結束有兩個含義：搜索成功並保存結果何搜索失敗並返回上一次狀態。
遞歸過程：傳遞當前狀態給下一次遞歸進行搜索。

模板

let res = [];   //存儲結果

function backtrack(path,condition,...){
    if(judge(condition)){  //滿足條件
        res.push(path);
        return;
    }
    for(let select of selectList){
        if(剪枝條件) break;
        path.push(select);  // 走某條路
        backtrack(path,newSelectList);
        path.pop(); //返回上一個十字路口
    }
}

適用場景

排列，組合
數組，字元串，給定一個特定的規則，嘗試找到某個解
二維數組下的DFS搜索

怎麼套用模板

我篩選了leetCode中hot和面試常考題庫中關於回溯的題目，題目由易到難，覆蓋每個使用場景。

子集

給定一組不含重複元素的整數數組 nums，返回該數組所有可能的子集（冪集）。

定義res數組存儲結果
每個子集為狀態變數，集合的元素個數為條件變數
子集的元素數量小於等於集合的元素數量為限制條件，滿足條件時添加到結果數組，否則回退到上一步
下一層搜索的集合需要去掉已添加到狀態變數中的元素

var subsets = function(nums) {
    let res = [];
    let n = nums.length;
    function back(path,i){
        if(i <= n){
            res.push(path);
        }
        for(let j = i;j < n;j++){
            path.push(nums[j]);
            back(path.slice(0),j+1);
            path.pop();
        }
    }
    back([],0);
    return res;
};

針對這道題還有一種比較酷的解法，利用二進位

一個集合的右2^n個子集
使用二進位模擬，每位為取或不取
舉個例子：[1,2,3] => 符號位： 001 010 100 => 0-7與之&

=> [] [001] [010] [001,010] [100] [001,100] [010,100] [001,010,100] 剛好八種，並且對應數組下標。

var subsets = function(nums) {
    let n = 1 << nums.length;
    let res = [];
    for(let i = 0;i < n;i++){
        let temp = [];
        for(let j = 0;j < nums.length;j++){
            if(i & (1 << j)){
                temp.push(nums[j]);
            }
        }
        res.push(temp);
    }
    return res;
};

全排列

給定一個 沒有重複 數字的序列，返回其所有可能的全排列。

定義res
每個排列序列為狀態變數，排列序列中集合的個數為條件變數
當排列序列的元素個數等於給定序列時，滿足條件
下一層遞歸依賴於上一層遞歸傳遞的路徑

var permute = function(nums) {
    let len = nums.length;
    let res = [];
    
    function back(path){
        if(path.length === len){
            res.push(path);
            return;
        }
        for(let i = 0;i < len;i++){
            if(path.indexOf(nums[i]) === -1){	//這裡的判斷很精髓
                path.push(nums[i]);
                back(path.slice());
                path.pop();
            }
        }
    }
    back([]);
    return res;
};

組合總和

給定一個無重複元素的數組 candidates 和一個目標數 target ，找出 candidates 中所有可以使數字和為 target 的組合。candidates 中的數字可以無限制重複被選取。

定義res
每個子數組為狀態變數，目標值為條件變數
子數組中的值相加等於目標值則滿足要求
下一層遞歸的tar（與目標值相差的數目）依賴於上一層遞歸的選擇

var combinationSum = function(candidates, target) {
    let res = [];
    let len = candidates.length;
    //這裡排序是為了防止在for循環if判斷時直接跳出了，比如這樣的樣例[8,7,4,3],11
    candidates.sort((x,y) => x-y);	
    function back(path,i,tar){
        if(tar === 0){
            res.push(path);
            return;
        }
        for(let j = i;j < len;j++){
            //判斷是否當前的路口都是通向死路
            if(tar < candidates[j]) break;          
            path.push(candidates[j]);
            back(path.slice(),j,tar-candidates[j]);
            path.pop();
        }
    }
    back([],0,target);
 
    return res;
};

分割迴文串

給定一個字元串 s，將 s 分割成一些子串，使每個子串都是迴文串。

返回 s 所有可能的分割方案。

定義res
狀態變數為迴文子串集，條件變數為子串集的字元串數目
當子串集的字元串數目與目標串長度相同時，滿足要求
下層遞歸的開始位置由上層遞歸決定

var partition = function(str){
    let res = [];
    function isPalindrome(s){
        let head = 0;
        let tail = s.length-1;
        while(head <= tail){
            if(s[head] !== s[tail]) return false;
            head++;
            tail--;
        }
        return true;
    }
    function backtrack(path,start){
    if(start === str.length) res.push(path);
        for(let i = start;i < str.length;i++){
            if(!isPalindrome(str.slice(start,i+1))) continue;
            path.push(str.slice(start,i+1));
            backtrack(path.slice(),i+1);
            path.pop();
        }
    }
    backtrack([],0);
    return res;
}

單詞搜索

給定一個二維網格和一個單詞，找出該單詞是否存在於網格中。

單詞必須按照字母順序，通過相鄰的單元格內的字母構成，其中「相鄰」單元格是那些水平相鄰或垂直相鄰的單元格。同一個單元格內的字母不允許被重複使用。

狀態變數為一條通路，條件變數為通路的長度
當通路與目標辭彙長度一致時，滿足條件
下一層遞歸的初始坐標和通路長度由上層遞歸決定

var exist = function (board, word) {
  //越界處理
  board[-1] = []
  board.push([])

  //尋找首個字母
  for (let y = 0; y < board.length; y++) {
    for (let x = 0; x < board.length; x++) {
      if (word[0] === board[y][x] && backtrack(y, x, 0)) return true
    }
  }
  
  //回溯
  function backtrack(y, x, i) {
    //回溯終止
    if (i + 1 === word.length) return true

    //保存字母
    var tmp = board[y][x]
    board[y][x] = false

    if (board[y][x + 1] === word[i + 1] && backtrack(y, x + 1, i + 1)) return true
    if (board[y][x - 1] === word[i + 1] && backtrack(y, x - 1, i + 1)) return true
    if (board[y + 1][x] === word[i + 1] && backtrack(y + 1, x, i + 1)) return true
    if (board[y - 1][x] === word[i + 1] && backtrack(y - 1, x, i + 1)) return true

    //復原字母
    board[y][x] = tmp
  }

  return false
};

排序演算法

冒泡排序

比較兩個記錄鍵值的大小，如果這兩個記錄鍵值的大小出現逆序，則交換這兩個記錄

function bubbleSort(arr){
    for(let i = 1;i < arr.length;i++){
        for(let j = i;j > 0;j--){
            if(arr[j] < arr[j-1]){
                [arr[j],arr[j-1]] = [arr[j-1],arr[j]];
            }
        }
    }
    return arr;
}

快排

在n個記錄中取某一個記錄的鍵值為標準，通常取第一個記錄鍵值為基準，通過一趟排序將待排的記錄分為小於或等於這個鍵值的兩個獨立的部分，這是一部分的記錄鍵值均比另一部分記錄的鍵值小，然後，對這兩部分記錄繼續分別進行快速排序，以達到整個序列有序

function quickSort(arr){
    if(arr.length <= 1) return arr;
    let right = [],left = [],keys = arr.shift();
    for(let value of arr){
        if(value > keys){
            right.push(value)
        }else{
            left.push(value);
        }
    }
    return quickSort(left).concat(keys,quickSort(right));
}

插入排序

第i（i大於等於1）個記錄進行插入操作時，R1、 R2，…，是排好序的有序數列，取出第i個元素，在序列中找到一個合適的位置並將她插入到該位置上即可。

function insertSort(arr){
    for(let i = 1;i < arr.length;i++){
        let j = i-1;
        if(arr[i]<arr[j]){
            let temp = arr[i];
            while(j >= 0 && temp < arr[j]){
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = temp;
        }
    }
    return arr;
}

希爾排序

演算法先將要排序的一組數按某個增量d（n/2,n為要排序數的個數）分成若干組，每組中記錄的下標相差d.對每組中全部元素進行直接插入排序，然後再用一個較小的增量（d/2）對它進行分組，在每組中再進行直接插入排序。當增量減到1時，進行直接插入排序後，排序完成。

function hillSort(arr){
    let len = arr.length;
    for(let gap = parseInt(len >> 1);gap >= 1;gap = parseInt(gap >> 1)){
        for(let i = gap;i < len;i++){
            if(arr[i] < arr[i-gap]){
                let temp = arr[i];
                let j = i - gap;
                while(j >= 0 && arr[j] > temp){
                    arr[j+gap] = arr[j];
                    j -= gap;
                }
                arr[j+gap] = temp;
            }
        }
    }
    return arr;
}

選擇排序

在第i次選擇操作中，通過n-i次鍵值間比較，從n-i+1個記錄中選出鍵值最小的記錄，並和第i（1小於等於1小於等於n-1）個記錄交換

function selectSort(arr){
    for(let i = 0;i < arr.length;i++){
        let min = Math.min(...arr.slice(i));
        let index = arr.indexOf(min);
        [arr[i],arr[index]] = [arr[index],arr[i]];
    }
    return arr;
}

堆排序

function adjustMaxHeap(heap,head,heapSize){
    let temp = heap[head];
    let child = head * 2 + 1;
    while(child < heapSize){
        if(child+1 < heapSize && heap[child] < heap[child+1]) child++;
        if(heap[head] < heap[child]){
            heap[head] = heap[child];
            head = child;
            child = head * 2 + 1;
        }else break;
        heap[head] = temp;
    }
}

function buildHeap(heap){
    for(let i = (heap.length-1) >> 1;i >= 0;i--){
        adjustMaxHeap(heap,i,heap.length);
    }
}

function heapSort(arr){
    buildHeap(arr);
    for(let i = arr.length-1;i > 0;i--){
        [arr[i],arr[0]] = [arr[0],arr[i]];
        adjustMaxHeap(arr,0,i);
    }
    return arr;
}

歸併排序

把一個有n個記錄的無序文件看成是由n個長度為1的有序子文件組成的文件，然後進行兩兩歸併

function MergeSort(arr,left,right){
    if(left >= right) return;
    let mid = Math.floor((right - left) >> 1) + left;
    MergeSort(arr,left,mid);
    MergeSort(arr,mid+1,right);
    Merge(arr,left,mid,right);
    return arr;
}
function Merge(arr,left,mid,right){
    let temp = [],i = 0;
    let p1 = left,p2 = mid + 1;
    while(p1 <= mid && p2 <= right){
        arr[p1] <= arr[p2] ? temp[i++] = arr[p1++] : temp[i++] = arr[p2++];
    }
    while(p1 <= mid){
        temp[i++] = arr[p1++];
    }
    while(p2 <= right){
        temp[i++] = arr[p2++];
    }
    for(let i = 0;i < temp.length;i++){
        arr[i+left] = temp[i];
    }
}

桶排序

把數據分組，放在一個個的桶中，然後對每個桶裡面的在進行排序

function radixSort(arr,arrDomain,gropSize){
    let data = [];
    for(let i = 0;i < arr.length;i++) data.push([]);
    console.log(data)
    for(let i = 0;i < arr.length;i++){
        data[Math.floor(parseInt(arr[i] / gropSize)) + 1].push(arr[i]);
    }
    for(let i = 0;i < data.length;i++){
        quickSort(data[i]);
    }
    return data.flat(Infinity);
}

各排序演算法的穩定性，時間複雜度，空間複雜度

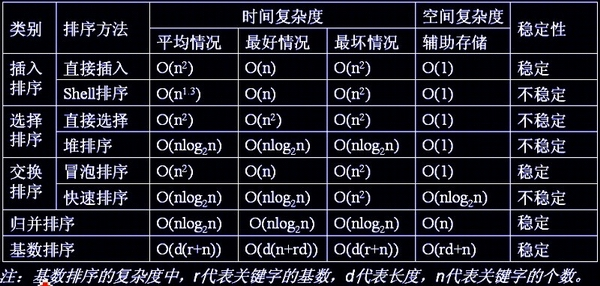
系統自帶排序實現

每個語言的排序內部實現都是不同的。

對於 JS 來說，數組長度大於 10 會採用快排，否則使用插入排序。選擇插入排序是因為雖然時間複雜度很差，但是在數據量很小的情況下和 O(N * logN) 相差無幾，然而插入排序需要的常數時間很小，所以相對別的排序來說更快。

穩定性

穩定性的意思就是對於相同值來說，相對順序不能改變。通俗的講有兩個相同的數 A 和 B，在排序之前 A 在 B 的前面，而經過排序之後，B 跑到了 A 的前面，對於這種情況的發生，我們管他叫做排序的不穩定性。

穩定性有什麼意義？個人理解對於前端來說，比如我們熟知框架中的虛擬 DOM 的比較，我們對一個“列表進行渲染，當數據改變後需要比較變化時，不穩定排序或操作將會使本身不需要變化的東西變化，導致重新渲染，帶來性能的損耗。

排序面試題目

快速排序在完全無序的情況下效果最好，時間複雜度為O(nlogn)，在有序情況下效果最差，時間複雜度為O(n^2)。
外部排序常用的演算法是歸併排序。
數組元素基本有序的情況下，插入排序效果最好，因為這樣只需要比較大小，不需要移動，時間複雜度趨近於O(n)。
如果只想得到1000個元素組成的序列中第5個最小元素之前的部分排序的序列，用堆排序方法最快。
對長度為 n 的線性表作快速排序，在最壞情況下，比較次數為 n(n-1)/2。

練習題

排序鏈表

在 O(n log n) 時間複雜度和常數級空間複雜度下，對鏈表進行排序。

var sortList = function(head) {
    let mergeList = (left,right) => {
        let res = new ListNode(0);
        let pre = res;
        while(left && right){
            if(left.val <= right.val){
                pre.next = left;
                left = left.next;
            }else{
                pre.next = right;
                right = right.next;
            }
            pre = pre.next;
        }
        pre.next = left ? left : right;
        return res.next;
    }
    let mergeSort = (node) => {
        if(!node || !node.next) return node;
        let mid = node;
        let fast = node.next;
        while(fast && fast.next){
            mid = mid.next;
            fast = fast.next.next;
        }
        let rightList = mid.next;
        mid.next = null;
        let left = node;
        let right = rightList;
        return mergeList(mergeSort(left),mergeSort(right));
    }
    return mergeSort(head);
};

逆序對

在數組中的兩個數字，如果前面一個數字大於後面的數字，則這兩個數字組成一個逆序對。輸入一個數組,求出這個數組中的逆序對的總數P。並將P對1000000007取模的結果輸出。即輸出P%1000000007

let count = 0;
function InversePairs(data)
{
    if (data == null || data.length == 0) {
        return 0;
    }
    MergeSort(data,0,data.length-1);
    return count % 1000000007;
}
function MergeSort(arr,left,right){
    if(left >= right) return;
    let mid = Math.floor((right - left)>>1) + left;
    MergeSort(arr,left,mid);
    MergeSort(arr,mid+1,right);
    Merge(arr,left,mid,right);
}

function Merge(arr,left,mid,right) {
    let temp = [],i = 0;
    let p1 = left,p2 = mid + 1;
    while(p1 <= mid && p2 <= right){
        if(arr[p1] <= arr[p2]){
            temp[i++] = arr[p1++];
        }else{
            count += mid - p1 + 1;
            temp[i++] = arr[p2++];
        }
    }
    while(p1 <= mid){
        temp[i++] = arr[p1++];
    }
    while(p2 <= right){
        temp[i++] = arr[p2++];
    }
    for(let i = 0;i < temp.length;i++){
        arr[i+left] = temp[i];
    }
}

並查集

屬於一種特殊的數據結構，在解決連通域問題上有著不錯的性能。

三個組件

維護一個數組let parents = []，存放當前節點的父節點，根節點的父節點是它本身。

查詢一個節點的根節點是哪個節點。

function find(root){
    let temp,son = root;
    while(root !== parents[root]){
        root = parents[root];
    }
    while(son !== root){	//路徑壓縮，其實就是個扁平化處理的過程
        temp = parents[son];
        parents[son] = root;
        son = temp;
    }
    return root;
}

//遞歸版
function find(root){
    if(root !== parents[root]) parents[root] = find(parents[root]);
    return parents[root];
}

合併兩個連通域

function join(x,y){
    x = find(x);
    y = find(y);
	if(x !== y){
        parents[x] = y;
    }
}

練習題

島嶼數量

寫三大組件，初始話parents時將其鍵和值對應
判定當前節點四周是否存在陸地，如果有就將他們連接起來，如果沒有就將當前節點的父節點置反
求出parents數組中鍵和值依然相等的數目（即為連通域的數目）

var numIslands = function(grid) {
    let row = grid.length;
    if(row === 0) return 0;
    let col = grid[0].length;
    let parents = [];
    for(let i = 0;i < row;i++){
        for(let j = 0;j < col;j++){
            parents[i*col+j] = i * col + j;
        }
    }
    function find(root){
        if(root !== parents[root]) parents[root] = find(parents[root]);
        return parents[root];
    }

    function union(x,y){
        x = find(x);
        y = find(y);
        if(x !== y){
            parents[x] = y;
        }
    } 
    for(let i = 0;i < row;i++){
        for(let j = 0;j < col;j++){
            if(grid[i][j] === '1'){
                i < row-1 && grid[i+1][j] === '1' && union((i+1)*col+j,i*col+j);
                j < col-1 && grid[i][j+1] === '1' && union(i*col+j+1,i*col+j);
            }else{
                parents[i*col+j] = -parents[i*col+j];
            }
        }
    }
    return parents.filter((value,key) => (key === value && Object.is(key,value))).length;
};

DFS的解法

var numIslands = function(grid) {
	const row = grid.length;
	if(!row) return 0;
	const col = grid[0].length;
	let res = 0;
	for(let i = 0; i < row; i++) {
		for(let j = 0; j < col; j++) {
			if(grid[i][j] === '1') {
				res++;
				dfs(grid, i, j);
			}
		}
	}
	function dfs(grid, i, j) {
		if(i < 0 || i >= row || j < 0 || j >= col) return;
		if(grid[i][j] === '1') {
			grid[i][j] = '0';
			dfs(grid, i - 1, j);
			dfs(grid, i + 1, j);
			dfs(grid, i, j - 1);
			dfs(grid, i, j + 1);
		}
	}
	return res;
};

被圍繞的區域

寫三大組件
將O節點劃分為內部節點和邊界節點，引入一個虛擬邊界root節點
判定O節點是否為內部節點，如果是則替換為X

var solve = function(board) {
    let row = board.length;
    if(row === 0) return board;
    let col = board[0].length;
    let parents = [];
    for(let i = 0;i < row;i++){
        for(let j = 0;j < col;j++){
            parents[i*col+j] = i * col + j;
        }
    }
    function find(root){
        if(root !== parents[root]) parents[root] = find(parents[root]);
        return parents[root];
    }

    function union(x,y){
        x = find(x);
        y = find(y);
        if(x !== y){
            parents[x] = y;
        }
    } 
    function isConnected(x,y){
        return find(x) === find(y);
    }
    let virtualArea = row * col + 1;
    for(let i = 0;i < row;i++){
        for(let j = 0;j < col;j++){
            if(board[i][j] === 'O'){
                if(i === 0 || i === row-1 || j === 0 || j === col-1){
                    union(i*col+j,virtualArea);
                }else{
                    i > 0 && board[i-1][j] === 'O' && union(i*col+j,(i-1)*col+j);
                    i < row-1 && board[i+1][j] === 'O' && union(i*col+j,(i+1)*col+j);
                    j > 0 && board[i][j-1] === 'O' && union(i*col+j,i*col+j-1);
                    j < col-1 && board[i][j+1] === 'O' && union(i*col+j,i*col+j+1);
                }
            }
        }
    }
    for(let i = 0;i < row;i++){
        for(let j = 0;j < col;j++){
            if(board[i][j] === 'O' && !isConnected(i*col+j,virtualArea)){
                board[i][j] = 'X';
            }
        }
    }
    return board;
};

拓撲排序

對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意一對頂點u和v，若邊<u,v>∈E(G)，則u在線性序列中出現在v之前。通常，這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列，簡稱拓撲序列。簡單的說，由某個集合上的一個偏序得到該集合上的一個全序，這個操作稱之為拓撲排序。不得不說百科的解釋很專業，但就是不知道在說什麼（wtcl）。

舉個例子

對於有向無環圖，我們首先找到一個入度為0的節點（隨便找一個）
刪除該節點，並將該節點的值存入結果數組，然後將該節點的所有鄰接節點的入度減1
重新尋找一個入度為0的節點，再重複操作2
將剩餘所有的入度為0的節點的值存入結果數組。

怎麼建圖

拓撲排序中涉及到節點的刪除，所以採用鄰接表的數據結構來表示圖是比較不錯的選擇

鄰接表

//這裡是一個簡單的鄰接表（面向試題編程），該結構在練習題部分有
class Node{
    constructor(value){
        this.value = value;
        this.next = null;
        this.in = 0;	//記錄入度
    }
}
class Graph{
    constructor(nodeNum,edges){
        this.list = new Array(nodeNum);
        for(let i = 0;i < this.list.length;i++){	//初始化鄰接表
            this.list[i] = new Node(i);
        }	
        let v1,v2,newNode = null;
        for(let edge of edges){	//構建鄰接表以及每個節點的入度數
            [v2,v1] = edge;
            newNode = new Node(v2);
            newNode.next = this.list[v1].next;
            this.list[v1].next = newNode;
            this.list[v2].in++;
        }
    }
}

喜聞樂見的練習題

課程表 II

現在你總共有 n 門課需要選，記為 0 到 n-1。

在選修某些課程之前需要一些先修課程。例如，想要學習課程 0 ，你需要先完成課程 1 ，我們用一個匹配來表示他們: [0,1]

給定課程總量以及它們的先決條件，返回你為了學完所有課程所安排的學習順序。

可能會有多個正確的順序，你只要返回一種就可以了。如果不可能完成所有課程，返回一個空數組。

建立鄰接表
創建一個輔助棧存放入度為零的節點，一個存放結果的結果數組res和一個記錄刪除節點數目的計數器count
每次取輔助棧中的節點，將其所有的鄰接節點入度減一併判斷入度是否為零（從而添加到輔助棧中），將節點值放入res，count++
判定計數器是否與圖的節點數相同，不相同證明有迴路，按題目要求返回值就好

class Node{
    constructor(value){
        this.value = value;
        this.next = null;
        this.in = 0;
    }
}
class Graph{
    constructor(nodeNum,edges){
        this.list = new Array(nodeNum);
        for(let i = 0;i < this.list.length;i++){
            this.list[i] = new Node(i);
        }
        let v1,v2,newNode = null;
        for(let edge of edges){
            [v2,v1] = edge;
            newNode = new Node(v2);
            newNode.next = this.list[v1].next;
            this.list[v1].next = newNode;
            this.list[v2].in++;
        }
    }
}
var findOrder = function(numCourses, prerequisites) {
    let list = new Graph(numCourses,prerequisites).list;
    let stack = [],res = [];
    for(let node of list){
        node.in === 0 && stack.push(node);
    }
    let count = 0;
    while(stack.length){
        let node = stack.pop();
        count++;
        res.push(node.value);
        while(node.next){
            (--list[node.next.value].in) === 0 && stack.push(list[node.next.value]);
            node = node.next;
        }
    }
    if(count !== list.length) return [];
    else return res;
};

課程表

你這個學期必須選修 numCourse 門課程，記為 0 到 numCourse-1 。

在選修某些課程之前需要一些先修課程。例如，想要學習課程 0 ，你需要先完成課程 1 ，我們用一個匹配來表示他們：[0,1]

給定課程總量以及它們的先決條件，請你判斷是否可能完成所有課程的學習？

//上題的簡化版，直接看程式碼吧
class Node{
    constructor(value){
        this.value = value;
        this.next = null;
        this.in = 0;
    }
}
class Graph{
    constructor(nodeNum,edges){
        this.list = new Array(nodeNum);
        for(let i = 0;i < this.list.length;i++){
            this.list[i] = new Node(i);
        }
        let v1,v2,newNode = null;
        for(let edge of edges){
            [v2,v1] = edge;
            newNode = new Node(v2);
            newNode.next = this.list[v1].next;
            this.list[v1].next = newNode;
            this.list[v2].in++;
        }
    }
}

var canFinish = function(numCourses, prerequisites) {
    let list = new Graph(numCourses,prerequisites).list;
    let stack = [];
    for(let node of list){
        node.in === 0 && stack.push(node);
    }
    let count = 0;
    while(stack.length){
        let node = stack.pop();
        count++;
        while(node.next){
            (--list[node.next.value].in) === 0 && stack.push(list[node.next.value]);
            node = node.next;
        }
    }
    return count === list.length
};

位運算

二進位中1的個數

請實現一個函數，輸入一個整數，輸出該數二進位表示中 1 的個數。例如，把 9 表示成二進位是 1001，有 2 位是 1。因此，如果輸入 9，則該函數輸出 2

//n & (n-1)每次1的數量--
var hammingWeight = function(n) {
    let count = 0;
    while(n){
        count++;
        n = n & (n-1);
    }
    return count;
};

數組中有一個數字出現的次數超過數組長度的一半，請找出這個數字

// 例如輸入一個長度為9的數組{1,2,3,2,2,2,5,4,2}。由於數字2在數組中出現了5次，超過數組長度的一半，因此輸出2。如果不存在則輸出0。
1. count初始化為0，count === 0時，res = 當前數，count++
2. 當前數與res相同count++，否則count--
3. 以上兩步能夠選出出現次數最多的數，接下來判斷它是否超過一半即可
function MoreThanHalfNum_Solution(numbers)
{
    let result,count=0;
    for(let i = 0;i < numbers.length;i++){
        if(count === 0){
            result = numbers[i];
            count++;
        }else{
            if(result === numbers[i]){
                count++;
            }else{
                count--;
            }
        }
    }
    let times = numbers.filter(x => x === result).length;
    return times > Math.floor(numbers.length >> 1) ? result : 0;
}

只出現一次的數字

給定一個非空整數數組，除了某個元素只出現一次以外，其餘每個元素均出現兩次。找出那個只出現了一次的元素

var singleNumber = function(nums) {
    let num = nums[0];
    for(let i = 1;i < nums.length;i++){
        num ^= nums[i];
    }
    return num;
};

比特位計數

給定一個非負整數 num。對於 0 ≤ i ≤ num 範圍中的每個數字 i ，計算其二進位數中的 1 的數目並將它們作為數組返回

1. 奇數1的個數等於前一個偶數＋1
2. 偶數1的個數等於當前偶數 >> 1 的值
var countBits = function(num) {
    let res = [0];
    for(let i = 1;i <= num;i++){
        if(i & 1){
            res[i] = res[i-1] + 1;
        }else{
            res[i] = res[i >> 1];
        }
    }
    return res;
};

漢明距離

兩個整數之間的漢明距離指的是這兩個數字對應二進位位不同的位置的數目。

給出兩個整數 x 和 y，計算它們之間的漢明距離

1. 亦或求出不同部分
2. 統計
var hammingDistance = function(x, y) {
    let ans = x ^ y,count = 0;
    while(ans){
        if(ans & 1) count++;
        ans = ans >> 1;
    }
    return count;
};

寫一個函數，求兩個整數之和，要求在函數體內不得使用+、-、*、/四則運算符號

1. ^ 不進位的加法
2. & 判斷進位點
3. << 1 進位
function Add(num1, num2)
{
    return num2 ? Add(num1 ^ num2,(num1 & num2) << 1) : num1;
}

雙指針

顧名思義，用兩個指針進行查找，提高查找的效率

n數之和

兩數之和

var twoSum = function(nums, target) {
    if(!nums.length) return [];
    let num = nums.slice(0);
    nums.sort((x,y) => x-y);
    let l = 0,r = nums.length-1;
    while(l < r){
        if(nums[l] + nums[r] === target) break;
        else if(nums[l] + nums[r] < target){
            l++;
        }else{
            r--;
        }
    }
    l = num.indexOf(nums[l]);
    r = num.indexOf(nums[r]) === l ? num.indexOf(nums[r],l+1) : num.indexOf(nums[r])
    return [l,r];
};

三數之和

var threeSum = function(nums) {
    if(nums.length < 3) return [];
    nums.sort((x,y) => x-y);
    let res = [];
    for(let i = 0;i < nums.length;i++){
        //如果第一個數大於1就沒必要排了
        if(nums[i] > 0) return res;
        //去重
        if(i && nums[i] === nums[i-1]) continue;
        let left = i+1,right = nums.length-1;
        while(left < right){
            if(nums[left] + nums[right] + nums[i] === 0){
                res.push([nums[i],nums[left],nums[right]]);
                //去重
                while(left < right && nums[left] === nums[left+1]){
                    left++;
                }
                while(left < right && nums[right] === nums[right-1]){
                    right--;
                }
                left++;
                right--;
            }else if(nums[left] + nums[right] + nums[i] > 0){
                right--;
            }else{
                left++;
            }
        }
    }
    return res;
};

最接近的三數之和

//思路與前面基本一致，但需要兩個變數，一個更新答案，一個更新最小差值
var threeSumClosest = function(nums, target) {
    if(!nums.length) return 0;
    let res = Infinity,mins = Infinity;
    nums.sort((x,y) => x-y);
    for(let i = 0;i < nums.length;i++){
        let left = i + 1,right = nums.length-1;
        while(left < right){
            mins = Math.min(Math.abs(nums[i]+nums[left]+nums[right]-target),mins);
            mins === Math.abs(nums[i]+nums[left]+nums[right]-target) 
            && (res = nums[i]+nums[left]+nums[right]);
            if(nums[i]+nums[left]+nums[right] < target){
                left++;
            }else if(nums[i]+nums[left]+nums[right] > target){
                right--;
            }else{
                break;
            }
        }
    }
    return res;
};

雨水，容器類問題

盛最多水的容器

//雙指針時刻更新最大值即可
var maxArea = function(height) {
    if(!height.length) return 0;
    let left = 0,right = height.length-1,res = 0;
    while(left < right){
        if(height[left] <= height[right]){
            let cur = height[left] * (right - left);
            res = Math.max(res,cur);
            left++;
        }else{
            let cur = height[right] * (right - left);
            res = Math.max(res,cur);
            right--;
        }
    }
    return res;
};

接雨水

function trap(arr){
    if(!arr.length) return 0;
    let left = 0,right = arr.length-1,leftHeight = 0,rightHeight = 0,res = 0;
    while(left < right){
        if(arr[left] < arr[right]){
            leftHeight = Math.max(arr[left],leftHeight);
            res += leftHeight - arr[left];
            left++;
        }else{
            rightHeight = Math.max(arr[right],rightHeight);
            res += rightHeight - arr[right];
            right--;
        }
    }
    return res;
}

鏈表類

刪除鏈表的倒數第n個節點

var removeNthFromEnd = function(head, n) {
    if(!head) return null;
    let fast = head,slow = head,pre = head,p1 = head,len = 0;
    while(p1){
        len++;
        p1 = p1.next;
    }
    //注意頭節點刪除的情況
    if(len === n) return head.next;
    while(n--){
        fast = fast.next;
    }
    while(fast){
        fast = fast.next;
        pre = slow;
        slow = slow.next;
    }
    pre.next = slow.next;
    return head;
};

請判斷一個鏈表是否為迴文鏈表

1. 將前半部分鏈表反轉
2. 判斷前後兩部分鏈表是否相等
var isPalindrome = function(head) {
    if(!head) return true;
    let pre = null,temp,fast = head,slow = head;
    while(fast && fast.next){
        temp = slow;
        fast = fast.next.next;
        slow = slow.next;
        temp.next = pre;
        pre = temp;
    }
    if(fast) slow = slow.next;
    while(pre && slow){
        if(pre.val !== slow.val) return false;
        pre = pre.next;
        slow = slow.next;
    }
    return true;
};

給定一個鏈表，判斷鏈表中是否有環

var hasCycle = function(head) {
    if(!head || !head.next || !head.next.next) return false;
    let fast = head.next.next,slow = head.next;
    while(fast !== slow){
        if(fast === null || fast.next === null) return false;
        fast = fast.next.next;
        slow = slow.next;
    }
    return true;
};

輸入一個鏈表，輸出該鏈表中倒數第k個結點。

function FindKthToTail(head, k)
{
    // write code here
    if(head === null || k === 0) return null;
    let fast = head,slow = head;
    while(k--){
        if(fast === null) return null;
        fast = fast.next;
    }
    while(fast){
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

輸入兩個單調遞增的鏈表，輸出兩個鏈表合成後的鏈表，當然我們需要合成後的鏈表滿足單調不減規則。

//注意與拷貝鏈表區分
function Merge(pHead1, pHead2)
{
    if(pHead1 === null){
        return pHead2;
    }else if(pHead2 === null){
        return pHead1;
    }
    if(pHead1.val < pHead2.val){
        pHead1.next = Merge(pHead1.next,pHead2);
        return pHead1;
    }else{
        pHead2.next = Merge(pHead2.next,pHead1);
        return pHead2;
    }
}

輸入兩個鏈表，找出它們的第一個公共結點

function FindFirstCommonNode(pHead1, pHead2)
{
    // write code here
    let p1 = pHead1,p2 = pHead2;
    while (p1 !== p2){
        p1 = p1 === null ? pHead2 : p1.next;
        p2 = p2 === null ? pHead1 : p2.next;
    }
    return p1;
}

找出環形鏈表入環位置

var detectCycle = function(head) {
    if(!head || !head.next) return null;
    let fast = head.next.next,slow = head.next,p1 = head;
    while(fast !== null && fast !== slow){
        if(fast.next) fast = fast.next.next;
        else fast = null;
        slow = slow.next;
    }
    if(fast === null) return null;
    else{
        while(p1 !== slow){
            p1 = p1.next;
            slow = slow.next;
        }
        return slow;
    }
};

字元串類

驗證迴文串

var isPalindrome = function(s) {
    let reg = /[a-z]|[0-9]/;
    s = s.split('').map(x => x.toLowerCase()).filter((x) => reg.test(x)).join('');
    let head = 0;
    let tail = s.length-1;
    while(head <= tail){
        if(s[head] !== s[tail]) return false;
        head++;
        tail--;
    }
    return true;
};

矩陣

順時針列印矩陣

輸入一個矩陣，按照從外向里以順時針的順序依次列印出每一個數字

// 例如，如果輸入如下4 X 4矩陣： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 則依次列印出數字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
旋轉魔方法，每次列印第一列，然後將矩陣逆時針旋轉
function rotate(arr){
    if(!arr.length) return [];
    let newArr = [];
    for(let i = 0;i < arr[0].length;i++){
        let temp = [];
        for(let j = 0;j < arr.length;j++){
            temp.push(arr[j][arr[0].length-1-i]);
        }
        newArr.push(temp);
    }
    return newArr;
}
function printMatrix(matrix)
{
    if(!matrix.length) return [];
    let ans = [];
    while(matrix.length){
        for(let i = 0;i < matrix[0].length;i++){
            ans.push(matrix[0][i])
        }
        matrix.splice(0,1);
        matrix = rotate(matrix);
    }
    return ans;
}

旋轉影像

給定一個 n × n 的二維矩陣表示一個影像。

將影像順時針旋轉 90 度

var rotate = function(matrix) {
    if(!matrix.length) return [];
    let left = 0,right = matrix.length-1;
    while(right-left > 0){
        [matrix[left],matrix[right]] = [matrix[right],matrix[left]];
        left++;
        right--;
    }
    for(let i = 0;i < matrix.length;i++){
        for(let j = i+1;j < matrix[i].length;j++){
            [matrix[i][j],matrix[j][i]] = [matrix[j][i],matrix[i][j]];
        }
    }
    return matrix;
};

螺旋矩陣 II

給定一個正整數 n，生成一個包含 1 到 n2 所有元素，且元素按順時針順序螺旋排列的正方形矩陣

//基本就是模擬這個過程，要注意轉彎的邊界條件
var generateMatrix = function(n) {
    let rows = n-1,cols = n-1,col = 0,row = 0,iter = 1,x_dire = 1,y_dire = 1,cur_dire = 1,res = [];
    for(let i = 0;i < n;i++) res.push([]);
    while(iter <= n ** 2) {
        if (cur_dire === 1 && res[row][col] === undefined) {
            res[row][col] = iter;
            iter++;
            if (x_dire === 1) {
                if (col < cols) {
                    col++;
                } else {
                    cur_dire = -1;
                    x_dire = -x_dire;
                    if (y_dire === 1) row++;
                    else row--;
                }
            } else {
                if (col > 0) {
                    col--;
                } else {
                    cur_dire = -1;
                    x_dire = -x_dire;
                    if (y_dire === 1) row++;
                    else row--;
                }
            }
        }else if (cur_dire === 1 && res[row][col]) {
            if (y_dire === 1) row++;
            else row--;
            x_dire = -x_dire;
            cur_dire = -1;
            if (x_dire === 1) col++;
            else col--;
        }else if (cur_dire === -1 && res[row][col] === undefined) {
            res[row][col] = iter;
            iter++;
            if (y_dire === 1) {
                if (row < rows) {
                    row++;
                } else {
                    cur_dire = 1;
                    y_dire = -y_dire;
                    if (x_dire === 1) col++;
                    else col--;
                }
            } else {
                if (row >= 0) {
                    row--;
                } else {
                    cur_dire = 1;
                    y_dire = -y_dire;
                    if (x_dire === 1) col++;
                    else col--;
                }
            }
        } else if(cur_dire === -1 && res[row][col]) {
            if (x_dire === 1) col++;
            else col--;
            y_dire = -y_dire;
            cur_dire = 1;
            if (y_dire === 1) row++;
            else row--;
        }
    }
    return res;
};

矩陣置零

給定一個 m x n 的矩陣，如果一個元素為 0，則將其所在行和列的所有元素都設為 0。請使用原地演算法

//利用了js的特性，-0和0的不相等
//將0所在行列中非0元素置為-0
var setZeroes = function(matrix) {
    for(let i = 0;i < matrix.length;i++){
        for(let j = 0;j < matrix[i].length;j++){
            if(Object.is(matrix[i][j],0)){
                for(let k = 0;k < matrix.length;k++){
                    if(k !== i && Object.is(matrix[k][j],0)) continue;
                    else matrix[k][j] = -0
                }
                for(let k = 0;k < matrix[i].length;k++){
                    if(k !== j && Object.is(matrix[i][k],0)) continue;
                    else matrix[i][k] = -0
                }                
            }
        }
    }
    return matrix;
};

楊輝三角

//入坑題
function print(n) {
    let arr = [],n1 = n;
    while(n1--){
        arr.push([]);
    }
    for(let i = 0;i < n;i++){
        for(let j = 0;j <= i;j++){
            if(j === 0 || j === i) arr[i][j] = 1;
            else{
                arr[i][j] = arr[i-1][j-1]+arr[i-1][j];
            }
        }
    }
    arr.forEach(x => console.log(x.toString().replace(/,/g,' ')));
}

二叉樹

遍歷系列

二叉樹的前中後序遍歷（遞歸和非遞歸）

//遞歸
function pre(root){
    if(!root) return root;
    console.log(root.val);
    pre(root.left);
    pre(root.right);
}

function mid(root){
    if(!root) return root;
    mid(root.left);
    console.log(root.val);
    mid(root.right);
}

function next(root){
    if(!root) return root;
    next(root.right);
    next(root.left);
    console.log(root.val);
}

//非遞歸
//前序
//用棧進行模擬
//每次將棧頂元素添加到結果中，然後將棧頂元素的左右非空子樹入棧（注意右子樹先入棧，後彈出）
//直到棧為空跳出循環
function pre(root){
    if(root === null) return root;
    let res = [],stack = [];
    stack.push(root);
    while (stack.length){
        let node = stack.pop();
        res.push(node.val);
        node.right && stack.push(node.right);
        node.left && stack.push(node.left);
    }
    return res;
}

//中序
//對棧頂元素深度遍歷左子樹入棧，然後將棧頂添加到結果中，然後訪問當前子節點的右子樹，依次循環
function mid(root){
    if(root === null) return root;
    let res = [],stack = [];
    stack.push(root);
    while (stack.length){
        while(root !== null){
            stack.push(root);
            root = root.left;
        }
        let node = stack.pop()
        res.push(node.val);
        root = node.right;
    }
    //根節點添加了兩次
    return res.slice(0,res.length-1);
}

//後序
//與前序相似，但生成順序為根右左，最後將res反序
function next(root){
    if(root === null) return root;
    let res = [],stack = [];
    stack.push(root);
    while (stack.length){
        let node = stack.pop();
        res.push(node.val);
        node.left && stack.push(node.left);
        node.right && stack.push(node.right);
    }
    return res.reverse();
}

層次遍歷

var levelOrder = function(root) {
    if(!root) return [];
    let nodes = [],queue = [root],path=[];
    let cur = 1,next = 0;
    while(queue.length){
        let node = queue.shift();
        path.push(node.val);
        node.left && queue.push(node.left) && next++;
        node.right && queue.push(node.right) && next++;
        cur--;
        if(!cur){
            nodes.push(path);
            path = [];
            cur = next;
            next = 0;
        }
    }
    return nodes;
};

遍歷變種

二叉樹的鋸齒形層次遍歷

給定一個二叉樹，返回其節點值的鋸齒形層次遍歷。（即先從左往右，再從右往左進行下一層遍歷，以此類推，層與層之間交替進行）。

var zigzagLevelOrder = function(pRoot) {
    if(!pRoot) {
        return []
    }
    var queue = [], res = [], temp = [],
        node, level = 0, toBePrinted = 1, isEven = true;
    queue.push(pRoot);
    while(queue.length) {
        node = queue.shift();
        // 判斷當前行為奇數行還是偶數行
        if(isEven) {
            temp.push(node.val);
        } else {
            temp.unshift(node.val);
        }
        // 計算每一行的元素個數
        if(node.left) {
            queue.push(node.left);
            level++;
        }
        if(node.right) {
            queue.push(node.right);
            level++;
        }
        toBePrinted--;
        // 判斷當前行是否全部輸出完畢
        if(toBePrinted === 0) {
            res.push(temp);
            temp = [];
            toBePrinted = level;
            level = 0;
            isEven = !isEven;
        }
    }
    return res;
};

從上到下按層列印二叉樹，同一層結點從左至右輸出。每一層輸出一行。

//相比bfs，需要增加兩個變數，一個存當前層次的還有多少節點需要列印，一個存儲下一層次有多少個節點（每次隊列push時進行++）
function Print(pRoot) {
    let nodes = [],queue = [pRoot],path=[];
    let cur = 1,next = 0;
    while(queue.length){
        let node = queue.shift();
        path.push(node.val);
        node.left && queue.push(node.left) && next++;
        node.right && queue.push(node.right) && next++;
        cur--;
        if(!cur){
            nodes.push(path);
            path = [];
            cur = next;
            next = 0;
        }
    }
    return nodes;
}

根據已知二叉樹，求某值

求二叉樹的深度

function TreeDepth(pRoot)
{
    if(pRoot === null) return 0;
    let left = TreeDepth(pRoot.left);
    let right = TreeDepth(pRoot.right);
    return Math.max(left,right) + 1;
}

二叉搜索樹中第K小的元素

var kthSmallest = function(root, k) {
    let res;
    function midOrder(root){
        if(!root) return root;
        midOrder(root.left);
        if(k === 0) return res;
        else{
            res = root.val;
            k--;
        }
        midOrder(root.right);
    }
    midOrder(root);
    return res;
};

二叉樹最近公共祖先

（1）深度優先查找，查到兩節點任意一個返回
（2）當兩個節點都找到時返回root，否則返回null
var lowestCommonAncestor = function(root, p, q) {
    if(!root) return null;
    if(root === p || root === q) return root;
    let left = lowestCommonAncestor(root.left,p,q);
    let right = lowestCommonAncestor(root.right,p,q);
    if(!left) return right;
    if(!right) return left;
    if(left && right) return root;  
    return null;
};

給定一棵二叉樹，你需要計算它的直徑長度。

一棵二叉樹的直徑長度是任意兩個結點路徑長度中的最大值。這條路徑可能穿過也可能不穿過根結點。

易錯點是直徑可能不經過根節點
用max保存最大值，
當每個節點作為根節點時，與max比較進行更新
var diameterOfBinaryTree = function(root) {
    let max = 0;
    function dfs(root){
        if(!root) return 0;
        let l = dfs(root.left);
        let r = dfs(root.right);
        max = Math.max(max,l+r);
        return Math.max(l,r)+1;
    }
    dfs(root);
    return max;
};

一些特殊的二叉樹（判斷和構建）

判斷二叉樹是否是對稱二叉樹

function mirrors(root)
{
    if(root === null) return root;
    [root.left,root.right] = [root.right,root.left];
    mirrors(root.left);
    mirrors(root.right);
}
var isSymmetric = function(root) {
    let mirror = JSON.parse(JSON.stringify(root));
    mirrors(mirror);
    if(JSON.stringify(mirror) === JSON.stringify(root)){
        return true;
    }else{
        return false;
    }
};

驗證二叉搜索樹

給定一個二叉樹，判斷其是否是一個有效的二叉搜索樹。

let pre = -Infinity;
var isValidBST = function(root) {
    if(!root) return true;
    let left = isValidBST(root.left);
    if(root.val <= pre || !left) return false;
    pre = root.val;
    return isValidBST(root.right);
};

從前序與中序遍歷序列構造二叉樹

var buildTree = function(preorder, inorder) {
    if(!preorder.length || !inorder.length) return null;
    let root = new TreeNode(preorder[0]);
    let key = 0;
    for(let i = 0;i < inorder.length;i++){
        if(inorder[i] === preorder[0]){
            key = i;
            break;
        }
    }
    root.left = buildTree(preorder.slice(1,key+1),inorder.slice(0,key));
    root.right = buildTree(preorder.slice(key+1),inorder.slice(key+1));
    return root;
};

翻轉二叉樹

var invertTree = function(root) {
    if(root === null) return root;
    [root.left,root.right] = [root.right,root.left];
    invertTree(root.left);
    invertTree(root.right);
    return root;
};

把二叉搜索樹轉換為累加樹

var convertBST = function(root) {
    let cur = 0;
    re = function(root){
        if(!root) return root;
        re(root.right);
        root.val += cur;
        cur = root.val;
        re(root.left);
        return root;
    }
    return re(root);
};

合併二叉樹

var mergeTrees = function(t1, t2) {
    if(t1 && t2){
        t1.val += t2.val;
        t1.left = mergeTrees(t1.left,t2.left);
        t1.right = mergeTrees(t1.right,t2.right);
    }
    return t1 || t2;
};

輸入兩棵二叉樹A，B，判斷B是不是A的子結構

（ps：我們約定空樹不是任意一個樹的子結構）

function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
}
//判斷是否為子結構跟先序遍歷類似
function isSubtree(root1,root2) {
    if(!root2) return true;
    if(!root1) return false;
    if(root1.val !== root2.val) return false;
    return isSubtree(root1.left,root2.left) && isSubtree(root1.right,root2.right);
}
//從根節點開始遞歸判斷是否含有子結構
function HasSubtree(pRoot1, pRoot2)
{
    if(!pRoot1 || !pRoot2) return false;
    return (
        isSubtree(pRoot1,pRoot2)
        || HasSubtree(pRoot1.left,pRoot2)
        || HasSubtree(pRoot1.right,pRoot2)
    )
}

操作給定的二叉樹，將其變換為源二叉樹的鏡像

function Mirror(root)
{
    if(root === null) return root;
    [root.left,root.right] = [root.right,root.left];
    Mirror(root.left);
    Mirror(root.right);
    return root;
}

輸入一棵二叉樹，判斷該二叉樹是否是平衡二叉樹

1. 比較兩顆子樹的高度，兩邊都取最大深度
2. 查看兩顆子樹高度差是否相差為1
3. 如果大於1，那麼將其標記為-1（表示不是AVL樹），然後每次遞歸時先判斷該節點的子樹是否時AVL樹
function IsBalanced_Solution(pRoot)
{
    return orderTree(pRoot) !== -1;
}
function orderTree(root) {
    if(!root) return 0;
    let left = orderTree(root.left);
    let right = orderTree(root.right);
    if(left === -1 || right === -1 || Math.abs(left-right) > 1) return -1;
    return Math.max(left,right)+1;
}

求二叉樹的一些路徑

路徑總和 III

給定一個二叉樹，它的每個結點都存放著一個整數值。

找出路徑和等於給定數值的路徑總數。

路徑不需要從根節點開始，也不需要在葉子節點結束，但是路徑方向必須是向下的（只能從父節點到子節點）。

二叉樹不超過1000個節點，且節點數值範圍是 [-1000000,1000000] 的整數。

function dfs(cur,sum,root,path,res){
    cur += root.val;
    path.push(root.val);
    if(cur === sum && !root.left && !root.right){
        res.push(path.slice(0));
    }
    root.left && dfs(cur,sum,root.left,path,res);
    root.right && dfs(cur,sum,root.right,path,res);
    path.pop();
}
var pathSum = function(root, sum) {
    if(!root) return [];
    let res = [],path = [],cur = 0;
    dfs(cur,sum,root,path,res);
    return res;
};

二叉樹中和為某一值的路徑

輸入一棵二叉樹和一個整數，列印出二叉樹中節點值的和為輸入整數的所有路徑。從樹的根節點開始往下一直到葉節點所經過的節點形成一條路徑。

// 路徑定義為從樹的根結點開始往下一直到葉結點所經過的結點形成一條路徑。(注意: 在返回值的list中，數組長度大的數組靠前)
1. dfs + 回溯
2. 深度搜索路徑，將路徑中的每個節點值相加，路徑存入快取，直到遍歷到最深處
3. 比較當前值是否為目標值，如果是將快取的路徑加入結果數組，如果不是則回退到上一個節點
function dfs(root,expectNumber,cur,path,result) {
    cur += root.val;
    path.push(root);
    if(cur === expectNumber && root.left === null && root.right === null){
        result.push(path.slice(0));
    }
    root.left && dfs(root.left,expectNumber,cur,path,result);
    root.right && dfs(root.right,expectNumber,cur,path,result);
    //重要
    path.pop();
}
function FindPath(root, expectNumber)
{
    let result = [],path = [],cur = 0;
    if(!root) return result;
    dfs(root,expectNumber,cur,path,result);
    return result;
}

二叉樹中的最大路徑和

給定一個非空二叉樹，返回其最大路徑和。

本題中，路徑被定義為一條從樹中任意節點出發，達到任意節點的序列。該路徑至少包含一個節點，且不一定經過根節點。

var maxPathSum = function(root) {
    let max = -Infinity;
    function dfs(root){
        if(!root) return 0;
        let l = Math.max(dfs(root.left),0);
        let r = Math.max(dfs(root.right),0);
        max = Math.max(max,l + r + root.val);
        return Math.max(l,r)+root.val;
    }
    dfs(root);
    return max;
};

其他

不同的二叉索引樹的個數

卡塔蘭數
dp[0] = 1
dp[i] = dp[i-1] * (4 * i + 2) / (i + 2);
var numTrees = function(n) {
    if(!n) return 0;
    let dp = [1];
    for(let i = 1;i < n;i++){
        dp[i] = dp[i-1] * (4 * i + 2) /(i + 2);
    }
    return dp[n-1];
};

根據js的依賴關係樹tree，輸出合理的打包順序的數組（阿里面試題）

function resolve(tree){
    let len = tree.require.length,queue = [];
    for(let i = 0;i < len;i++){
        queue.push([]);
    }
    tree = flatten(tree);
    let head = tree.name;
    for(let key in tree){
        let k = Number(key.slice(8,9));
        Object.keys(tree[key]).length && queue[k].push(tree[key])
    }
    let res = [];
    for(let i = queue.length-1;i >= 0;i--){
        for(let j = queue[i].length-1;j >= 0;j--){
            res.indexOf(queue[i][j]) === -1 && res.push(queue[i][j]);
        }
    }
    return res;
}
function flatten(input) {
    let res = {};
    let re = function(obj,key){
        if(obj instanceof Object && !(obj instanceof Array)){
            let empty = true;
            for(let i in obj){
                re(obj[i],key ? `${key}.${i}` : i)
            }
            if(empty && key){
                res[key] = {};
            }
        }else if(obj instanceof Array){
            if(obj.length){
                for(let i = 0;i < obj.length;i++){
                    re(obj[i],key ? `${key}[${i}]` : i)
                }
            }else{
                res[key] = [];
            }
        }else{
            if(obj !== undefined && obj !== null){
                res[key] = obj;
            }
        }
    };
    re(input,'');
    return res;
}
var tree1 = {
    name: 'main.js',
    require: [{
        name: 'A.js'
    }, {
        name: 'B.js'
    }] }

var tree2 = {
    name: 'page.js',
    require: [{
        name: 'A.js',
        require: [{
            name: 'B.js',
            require: [{
                name: 'C.js'
            }]
        }]},
        {
            name: 'D.js',
            require: [{
                name: 'C.js'
            }, {
                name: 'E.js'
            }]
        }] }
resolve(tree1) // ['A.js', 'B.js', 'main.js']
resolve(tree2) // ['C.js', 'E.js', 'D.js', 'B.js', 'A.js', 'page.js']

輸入一個整數數組，判斷該數組是不是某二叉搜索樹的後序遍歷的結果。如果是則輸出Yes,否則輸出No。假設輸入的數組的任意兩個數字都互不相同。

1. 後序遍歷的最後一個節點為根節點
2. 二叉索引樹右子樹大於根節點，左子樹小於根節點，所以可以用根節點將樹分為兩顆子樹
3. 二叉索引樹的子樹也是二叉索引樹，所以分別對子樹進行判斷，直到遍歷到最後一個節點
var verifyPostorder = function(postorder) {
    if(!postorder.length) return true;
    let tail = postorder.pop();
    let key = postorder.length;
    for(let i = 0;i < postorder.length;i++){
        if(postorder[i] > tail){
            key = i;
            break;
        }
    }
    for(let i = key+1;i < postorder.length;i++){
        if(postorder[i] < tail){
            return false;
        }
    }
    return verifyPostorder(postorder.slice(0));
};

輸入一棵二叉搜索樹，將該二叉搜索樹轉換成一個排序的雙向鏈表

var treeToDoublyList = function(root) {
    if(!root) return null;
    let head = null,tail = null,pre = null;
    function dfs(root){
        if(!root) return null;
        dfs(root.left);
        //第一個節點作為頭節點
        if(!pre) head = root;
        //將上一個節點的後繼指針指向當前節點
        else pre.right = root;
        //將當前指針的前驅指針指向上一個節點
        root.left = pre;
        //更新上一個節點
        pre = root; 
        //更新尾部節點
        tail = root;
        dfs(root.right);
    }
    dfs(root);
    //首尾連接
    head.left = tail;
    tail.right = head;
    return head;
};

二叉樹展開為鏈表

前序遍歷，將右子樹放到左子樹最右葉子節點的後面，將左子樹放到右子樹上，左子樹置空
var flatten = function(root) {
    function dfs(root){
        if(!root) return;
        dfs(root.left);
        dfs(root.right);
        let pre = root.left;
        if(pre){
            //獲取左子樹最右葉子節點
            while(pre.right){
                pre = pre.right;
            }
            //將右子樹放在左子樹最右右子節點後面
            pre.right = root.right;
            //將新構建的左子樹放在右子樹上
            root.right = root.left;
            //左子樹置空
            root.left = null;
        }
    }
    dfs(root);
    return root;
};

哈希表

面試中能用hashmap解的題往往有更優的解法，但hashmap不失為一種最容易想到和容易書寫的解法

每日溫度

根據每日氣溫列表，請重新生成一個列表，對應位置的輸出是需要再等待多久溫度才會升高超過該日的天數。如果之後都不會升高，請在該位置用 0 來代替。

例如，給定一個列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的輸出應該是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：氣溫列表長度的範圍是 [1, 30000]。每個氣溫的值的均為華氏度，都是在 [30, 100] 範圍內的整數。

var dailyTemperatures = function(T) {
    let res = [],len = T.length;
    while(len--){
        res.push(0);
    }
    for(let i = 0;i < T.length;i++){
        for(let j = i+1;j < T.length;j++){
            if(T[j] <= T[i]){
                res[i]++;
                if(j === T.length-1) res[i] = 0;
            }else{
                res[i]++;
                break;
            }
        }
    }
    return res;
};

字母異位詞分組

給定一個字元串數組，將字母異位片語合在一起。字母異位詞指字母相同，但排列不同的字元串

var groupAnagrams = function(strs) {
    if(!strs.length) return [];
    let str = strs.slice(0),res = [];
    strs = strs.map(x => x.split('').sort().join(''));
    let map = new Map();
    for(let i = 0;i < strs.length;i++){
        map.hasOwnProperty(strs[i]) ? map[strs[i]].push(str[i]) : (map[strs[i]] = [str[i]]); 
    }
    for(let key in map){
        res.push(map[key]);
    }
    return res;
};

和為K的子數組

給定一個整數數組和一個整數 k，你需要找到該數組中和為 k 的連續的子數組的個數

var subarraySum = function(nums, k) {
    if(!nums.length) return 0;
    let res = 0;
    for(let i = 0;i < nums.length;i++){
        let cur = 0;
        for(let j = i;j < nums.length;j++){
            cur += nums[j];
            if(cur === k) res++;
        }
    }
    return res;
};

前 K 個高頻元素

給定一個非空的整數數組，返回其中出現頻率前 k 高的元素

var topKFrequent = function(nums, k) {
    if(!nums.length) return [];
    let map = new Map();
    for(let i = 0;i < nums.length;i++){
        map.has(nums[i]) ? map.set(nums[i],map.get(nums[i])+1) : map.set(nums[i],1);
    }
    let values = [],res = [];
    for(let [k,i] of map){
        values.push(i);
    }
    values.sort((x,y) => y-x);
    values = values.slice(0,k);
    for(let [k,i] of map){
        if(values.indexOf(i) !== -1){
            res.push(k);
        }
    }
    return res;
};

在一個長度為n的數組裡的所有數字都在0到n-1的範圍內。數組中某些數字是重複的，但不知道有幾個數字是重複的。也不知道每個數字重複幾次。

// 請找出數組中任意一個重複的數字。 例如，如果輸入長度為7的數組{2,3,1,0,2,5,3}，那麼對應的輸出是第一個重複的數字2。
function duplicate(numbers, duplication)
{
    let map = new Map();
    for(let i = 0;i < numbers.length;i++){
        map.has(numbers[i]) ? map.set(numbers[i],map.get(numbers[i]) + 1) : map.set(numbers[i],1);
        if(map.get(numbers[i]) > 1){
            duplication[0] = numbers[i];
            return true;
        }
    }
    return false;
}

//解法2
function FindNumsAppearOnce(array)
{
    let n = array[0];
    for(let i = 1;i < array.length;i++){
        n ^= array[i];
    }
    let k = 1,pow = 1;
    while(n > k){
        pow++;
        k = 2 ** pow - 1;
    }
    n = (n-1) ^ k;
    let left,right;
    for(let i = 0;i < array.length;i++){
        if(array[i] & n){

            left = left ? left ^ array[i] : array[i];
        }else{
            right = right ? right ^ array[i] : array[i];
        }
    }
    return [left,right];
}

在一個字元串(0<=字元串長度<=10000，全部由字母組成)中找到第一個只出現一次的字元,並返回它的位置

// 如果沒有則返回 -1（需要區分大小寫）.
function FirstNotRepeatingChar(str)
{
    let map = new Map();
    for(let key of str){
        map.has(key) ? map.set(key,map.get(key)+1) : map.set(key,1);
    }
    for(let [key,value] of map){
        if(value === 1) return str.indexOf(key);
    }
    return -1;
}

計數質數

統計所有小於非負整數 n 的質數的數量

var countPrimes = function(n) {
    let count = 0;
    let signs = new Uint8Array(n);

    for (let i = 2; i < n; i++) {
        if (!signs[i - 1]) {
            count++;
            for (let j = i * i; j <= n; j += i) {
                signs[j - 1] = true;
            }
        }
    }
    return count;
};

把只包含質因子2、3和5的數稱作丑數

返回第k個丑數

//例如6、8都是丑數，但14不是，因為它包含質因子7。 習慣上我們把1當做是第一個丑數。求按從小到大的順序的第N個丑數。
1. 0-6都是丑數，返回其值即可
2. 使用t1-t3表示2，3，5公因子的個數，每次取最小的公因子值，初值為1
function GetUglyNumber_Solution(index)
{
    if(index < 7) return index;
    let res = [1];
    let t2 = 0,t3 = 0,t5 = 0;
    for(let i = 1;i < index;i++){
        res[i] = Math.min(res[t2]*2,res[t3]*3,res[t5]*5);
        res[i] === res[t2]*2 && t2++;
        res[i] === res[t3]*3 && t3++;
        res[i] === res[t5]*5 && t5++;
    }
    return res[index-1]
}

無重複字元的最長子串

給定一個字元串，請你找出其中不含有重複字元的 最長子串 的長度。

var lengthOfLongestSubstring = function(s) {
    if(!s.length) return '';
    let sub = '',res = '';
    for(let i = 0;i < s.length;i++){
        if(sub === ''){
            sub += s[i];
            if(i === s.length-1 && res.length < sub.length) res = sub;
        }else{
            if(sub.indexOf(s[i]) === -1){
                sub += s[i];
                if(i === s.length-1 && res.length < sub.length) res = sub;
            }else{
                if(sub.length > res.length) res = sub;
                sub = sub.substr(sub.indexOf(s[i])+1) + s[i];
            }
        }
    }
    return res.length;
};

棧和隊列

棧滿足先進後出，隊列滿足先進先出

用兩個棧來實現一個隊列，完成隊列的Push和Pop操作。隊列中的元素為int類型

1. 用出入棧進行模擬
2. 進隊列全部添加到入棧中
3. 出隊列檢查出棧是否為空，不為空則將棧頂元素出棧；為空則先將入棧中的所有元素壓入出棧
let in_stack = [],out_stack = [];

function push(value) {
    in_stack.push(value);
}

function pop() {
    if(!out_stack.length){
        while(in_stack.length > 0){
            out_stack.push(in_stack.pop())
        }
    }else{
        return out_stack.pop();
    }
}

定義棧的數據結構，請在該類型中實現一個能夠得到棧中所含最小元素的min函數（時間複雜度應為O（1）

1. 使用輔助棧存最小值
2. 入棧時檢查元素是否為最小值，若是則壓入主棧和輔助棧
3. 出棧時檢查主棧棧頂元素是否與輔助棧一致，若是則一起彈出
// 注意：保證測試中不會當棧為空的時候，對棧調用pop()或者min()或者top()方法。
let stack1 = [],stack2 = [];
function push(value) {
    if(value <= Math.min(...stack1) || stack1.length === 0){
        stack1.unshift(value);
        stack2.unshift(value);
    }else{
        stack1.unshift(value)
    }
}

function pop() {
    if(stack1.length > 0) {
        if (stack1[0] === stack2[0]) {
            stack1.shift();
            stack2.shift();
        } else {
            stack1.shift();
        }
    }
}

function top() {
    if(stack1.length > 0) {
        return stack1[0];
    }
}

function min() {
    if(stack2.length > 0) {
        return stack2[0];
    }
}

滑動窗口的最大值

給定一個數組 nums 和滑動窗口的大小 k，請找出所有滑動窗口裡的最大值。

1. 維護一個單調的雙向隊列
2. 新增元素與隊尾元素比較，比隊尾小直接添加，比隊尾大，彈出隊尾，直到找到該元素合適的位置
3. 每次將雙向隊列中隊首元素添加到結果中
var maxSlidingWindow = function(nums, k) {
    if (k === 0) return [];
    const length = nums.length;
    if (length === 0) return [];
    const deque = [];
    for (let i = 0; i < k; ++i) {
        cleanDeque(deque, nums, i, k);
        deque.push(i);
    }
    const res = [];
    res.push(nums[deque[0]]);
    for (let i = k; i < length; ++i) {
        cleanDeque(deque, nums, i, k);
        deque.push(i);
        res.push(nums[deque[0]]);
    }
    return res;
};

function cleanDeque(queue, arr, cur, k) {
    // 如果雙向隊列中，包含不是滑動窗口內的數，直接出隊
    if (queue.length && cur >= k + queue[0]) {
        queue.shift();
    }

    while (queue.length && arr[idx] > nums[queue[queue.length - 1]]) {
        queue.pop();
    }
}

有效的括弧

給定一個只包括 ‘(‘，’)’，'{‘，’}’，'[‘，’]’ 的字元串，判斷字元串是否有效。

有效字元串需滿足：

左括弧必須用相同類型的右括弧閉合。
左括弧必須以正確的順序閉合。

左括弧入棧，右括弧與棧頂比較是否匹配，匹配彈出棧頂，不匹配return false
查看棧是否為空
var isValid = function(s) {
    if(!s.length) return true;
    let stack = [];
    for(let i = 0;i < s.length;i++){
        if(s[i] === '(' || s[i] === '{' || s[i] === '['){
            stack.unshift(s[i]);
        }else{
            if(s[i] === ')'){
                if(stack[0] === '(') stack.shift();
                else{
                    return false;
                }
            }else if(s[i] === ']'){
                if(stack[0] === '[') stack.shift();
                else{
                    return false;
                }
            }else if(s[i] === '}'){
                if(stack[0] === '{') stack.shift();
                else{
                    return false;
                }
            }
        }
    }
    return stack.length === 0;
};

字元串解碼

給定一個經過編碼的字元串，返回它解碼後的字元串。

編碼規則為: k[encoded_string]，表示其中方括弧內部的 encoded_string 正好重複 k 次。注意 k 保證為正整數。

你可以認為輸入字元串總是有效的；輸入字元串中沒有額外的空格，且輸入的方括弧總是符合格式要求的。

此外，你可以認為原始數據不包含數字，所有的數字只表示重複的次數 k ，例如不會出現像 3a 或 2[4] 的輸入。

var decodeString = function(s) {
    // 用兩個棧來存放當前狀態，前者是重複次數，後者是累積字元串
    let repetStack=[],resStack=[];
    //拼接字元串
    let resStr = "";
    //表示重複次數
    let repet = 0;
    // 遍歷s
    for(let i=0;i<s.length;i++){
        let cur = s.charAt(i);
        if(cur == '['){
            //雙雙壓入棧中,保存當前狀態
            repetStack.push(repet);
            resStack.push(resStr);
            //置空，準備下面的累積
            repet = 0;
            resStr = "";
        }else if(cur == ']'){
            // 取出當前重複次數棧中的值，也就是當前字元串的重複次數
            let count = repetStack.pop();
            // 根據重複次數生成重複字元串，賦值給temp，和resStr拼接
            let temp = "";
            for(let i = 0;i<count;i++){
                temp += resStr;
            }
            // 和前面已經求得的字元串進行拼接
            resStr = resStack.pop() + temp;
        }else if(cur>='0' && cur<='9'){
            // repet累積
            repet = repet*10 + (cur-'0');
        }else{
            //字元累積
            resStr += cur;
        }
    }
    return resStr;
};

根據身高重建隊列

假設有打亂順序的一群人站成一個隊列。每個人由一個整數對(h, k)表示，其中h是這個人的身高，k是排在這個人前面且身高大於或等於h的人數。編寫一個演算法來重建這個隊列。

1. 按升高降序，身高相同的按人數升序排列
2. 將隊列的每個元素按序插入到索引位置
var reconstructQueue = function(people) {
    if(!people) return [];
    people.sort((x,y)=>{
        return x[0] === y[0] ? x[1]-y[1] : y[0] - x[0];
    });
    let res = [];
    for(let i = 0;i < people.length;i++){
        res.splice(people[i][1],0,people[i]);
    }
    return res;
};

中綴表達式轉後綴

//數字直接添加到result
//棧空，運算符直接入棧
//遇到左括弧直接入棧，遇到右括弧棧頂元素添加到result中然後彈棧，依次循環直到遇到左括弧，然後將左括弧彈棧
//遇到運算符，判斷運算符與棧頂元素的優先順序，將所有優先順序大於等於該運算符的棧頂彈棧，然後入棧該運算符
//將棧中剩餘的字元添加到result中
function toPoland(str){
    let stack = [],result = '';
    for(let i = 0;i < str.length;i++){
        if(!Object.is(Number(str[i]),NaN)){
            result += str[i];
        }else if(stack.length === 0 && Object.is(Number(str[i]),NaN)){
            result += ' ';
            stack.push(str[i]);
        }else if(str[i] === '('){
            stack.push(str[i])
        }else if(str[i] === ')'){
            result += ' ';
            while(stack[stack.length-1] !== '('){
                result += stack.pop();
            }
            stack.pop();
        }else if(str[i] === '*' || str[i] === '/'){
            while(stack[stack.length-1] === '*' || stack[stack.length-1] === '/'){
                result += ' ' + stack.pop();
            }
            result += ' ';
            stack.push(str[i]);
        }else if(str[i] === '+' || str[i] === '-'){
            while(stack[stack.length-1] === '*' || stack[stack.length-1] === '/' || stack[stack.length-1] === '+' || stack[stack.length-1] === '-'){
                result += ' ' + stack.pop();
            }
            result += ' ';
            stack.push(str[i]);
        }
    }
    while(stack.length){
        result += ' ' + stack.pop();
    }
    return result;
}

計算後綴表達式

1. 數字入棧
2. 運算符，棧頂作為右操作數，次棧頂作為左操作數
3. 將運算結果入棧
4. 棧最後一個值即為結果
function CalcRPN(str) {
    let stack = [];
    let num = '';
    for(let i = 0;i < str.length;i++){
        if(str[i] === ' '){
            if(num !== '') stack.push(Number(num));
            num = '';
        }else if(!Object.is(Number(str[i]),NaN)){
            num += str[i];
        }else if(str[i] === '+'){
            let right = stack.pop();
            let left = stack.pop();

            stack.push(left + right);
        }else if(str[i] === '-'){
            let right = stack.pop();
            let left = stack.pop();
            stack.push(left - right);
        }else if(str[i] === '*'){
            let right = stack.pop();
            let left = stack.pop();
            stack.push(left * right);
        }else if(str[i] === '/'){
            let right = stack.pop();
            let left = stack.pop();
            stack.push(left / right);
        }
    }
    return stack.pop();
}

輸入兩個整數序列，第一個序列表示棧的壓入順序，請判斷第二個序列是否可能為該棧的彈出順序。假設壓入棧的所有數字均不相等。

1. 模擬出棧的過程
2. 變數push棧，每次將一個元素壓入輔助棧
3. 判斷輔助棧是否為空的同時，pop棧的棧頂是否與輔助棧棧頂元素相同，如果都滿足則兩者出棧
4. 最後判斷輔助棧是否為空
// 例如序列1,2,3,4,5是某棧的壓入順序，序列4,5,3,2,1是該壓棧序列對應的一個彈出序列，但4,3,5,1,2就不可能是該壓棧序列的彈出序列。
// （注意：這兩個序列的長度是相等的）

function IsPopOrder(pushV, popV) {
    let stack = [],k = 0;
    for(let i = 0;i < pushV.length;i++){
        stack.unshift(pushV[i]);
        while(stack[0] && popV[k] && stack[0] === popV[k]){
            stack.shift();
            k++;
        }
    }
    return stack.length === 0;
}

鏈表

反轉鏈表

function ReverseList(pHead)
{
    // write code here
    if(pHead === null || pHead.next === null) return pHead;
    let pre = null,nex = null;
    while(pHead !== null){
        nex = pHead.next;
        pHead.next = pre;
        pre = pHead;
        pHead = nex;
    }
    return pre;
}

複雜鏈表的複製

請實現一個函數，複製一個複雜鏈表。在複雜鏈表中，每個節點除了有一個 next 指針指向下一個節點，還有一個 random 指針指向鏈表中的任意節點或者 null。

function Clone(pHead)
{
    // write code here
    if(pHead === null) return pHead;
    let p1 = pHead;
    while(p1 !== null){
        let node = new RandomListNode(p1.label);
        node.next = p1.next;
        p1.next = node;
        p1 = node.next;
    }
    p1 = pHead;
    while(p1 !== null){
        let node = p1.next;
        if(p1.random) node.random = p1.random.next;
        p1 = node.next;
    }
    p1 = pHead;
    let p2 = pHead.next;
    while(p1.next !== null){
        let node = p1.next;
        p1.next = node.next;
        p1 = node;
    }
    return p2;
}

合併兩個有序鏈表

將兩個升序鏈表合併為一個新的升序鏈表並返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的

var mergeTwoLists = function(l1, l2) {
    if(!l1) return l2;
    if(!l2) return l1;
    if(!l1 && !l2) return null;
    if(l1.val <= l2.val){
        l1.next = mergeTwoLists(l1.next,l2);
        return l1;
    }else{
        l2.next = mergeTwoLists(l1,l2.next);
        return l2;
    }
};

環形鏈表

給定一個鏈表，判斷鏈表中是否有環

var hasCycle = function(head) {
    if(!head || !head.next || !head.next.next) return false;
    let fast = head.next.next,slow = head.next;
    while(fast !== slow){
        if(fast === null || fast.next === null) return false;
        fast = fast.next.next;
        slow = slow.next;
    }
    return true;
};

環形鏈表 II

給定一個鏈表，返回鏈表開始入環的第一個節點。如果鏈表無環，則返回 null

var detectCycle = function(head) {
    if(!head || !head.next) return null;
    let fast = head.next.next,slow = head.next,p1 = head;
    while(fast !== null && fast !== slow){
        if(fast.next) fast = fast.next.next;
        else fast = null;
        slow = slow.next;
    }
    if(fast === null) return null;
    else{
        while(p1 !== slow){
            p1 = p1.next;
            slow = slow.next;
        }
        return slow;
    }
};

相交鏈表

編寫一個程式，找到兩個單鏈表相交的起始節點

var getIntersectionNode = function(headA, headB) {
    var pA = headA;
    var pB = headB;
    while(pA !== pB){
        pB = pB? pB.next: headA;
        pA = pA? pA.next: headB;
    }
    return pA;
};

複製帶隨機指針的鏈表

給定一個鏈表，每個節點包含一個額外增加的隨機指針，該指針可以指向鏈表中的任何節點或空節點

var copyRandomList = function(pHead) {
    if(pHead === null) return pHead;
    let p1 = pHead;
    while(p1 !== null){
        let node = new Node(p1.val);
        node.next = p1.next;
        p1.next = node;
        p1 = node.next;
    }
    p1 = pHead;
    while(p1 !== null){
        let node = p1.next;
        if(p1.random) node.random = p1.random.next;
        p1 = node.next;
    }
    p1 = pHead;
    let p2 = pHead.next;
    while(p1.next !== null){
        let node = p1.next;
        p1.next = node.next;
        p1 = node;
    }
    return p2;
};

字元串

電話號碼的字母組合

給定一個僅包含數字 2-9 的字元串，返回所有它能表示的字母組合。

給出數字到字母的映射如下（與電話按鍵相同）。注意 1 不對應任何字母。

var letterCombinations = function(digits) {
    let map = {
        '2': 'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'
    };
    let res = [];
    for(let o = 0;o < digits.length;o++){
        let temp = [];
        if(res.length){
            for(let i = 0;i < res.length;i++){
                for(let j = 0;j < map[digits[o]].length;j++){
                    temp.push(res[i]+map[digits[o]][j]);
                }
            }
            res = temp.slice(0);
        }else{
            for(let i = 0;i < map[digits[o]].length;i++){
                res.push(map[digits[o]][i]);
            }
        }
    }
    return res;
};

迴文子串

給定一個字元串，你的任務是計算這個字元串中有多少個迴文子串。

具有不同開始位置或結束位置的子串，即使是由相同的字元組成，也會被計為是不同的子串。

var countSubstrings = function(s) {
    let s2 = s.split('').reverse().join('');
    let sum = 0;
    const len = s.length;
    for (let i = 0; i < len; i++) {
        for (let j = i + 1; j <= len; j++) {
            if (s.substr(i, j - i) === s2.substr(len - j, j - i)) {
                sum += 1
            }
        }
    }
    return sum;
};

括弧生成

數字 n 代表生成括弧的對數，請你設計一個函數，用於能夠生成所有可能的並且 有效的 括弧組合

var generateParenthesis = function(n) {
    if(!n) return [];
    let res = [];
    function dfs(subs,left,right,n){
        if(left === n && right === n){
            res.push(subs);
            return;
        }
        if(left < right){
            return;
        }
        left < n && dfs(subs+'(',left+1,right,n);
        right < n && dfs(subs+')',left,right+1,n);
    }
    dfs('',0,0,n);
    return res;
};

最長公共前綴

編寫一個函數來查找字元串數組中的最長公共前綴。

如果不存在公共前綴，返回空字元串 ""

var longestCommonPrefix = function(strs) {
    if(!strs.length) return '';
    strs.sort();
    let a = strs[0],b = strs[strs.length-1],res = '';
    for(let i = 0;i < a.length;i++){
        if(i < b.length && a[i] === b[i]){
            res += a[i];
        }else break;
    }
    return res;
};

羅馬數字轉整數

羅馬數字包含以下七種字元: I， V， X， L，C，D 和 M。

字元          數值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，羅馬數字 2 寫做 II ，即為兩個並列的 1。12 寫做 XII ，即為 X + II 。 27 寫做 XXVII, 即為 XX + V + II 。

通常情況下，羅馬數字中小的數字在大的數字的右邊。但也存在特例，例如 4 不寫做 IIII，而是 IV。數字 1 在數字 5 的左邊，所表示的數等於大數 5 減小數 1 得到的數值 4 。同樣地，數字 9 表示為 IX。這個特殊的規則只適用於以下六種情況：

I 可以放在 V (5) 和 X (10) 的左邊，來表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左邊，來表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左邊，來表示 400 和 900。

給定一個羅馬數字，將其轉換成整數。輸入確保在 1 到 3999 的範圍內。

//首先建立一個HashMap來映射符號和值，然後對字元串從左到右來，如果當前字元代表的值不小於其右邊，就加上該值；否則就減去該值。以此類推到最左邊的數
var romanToInt = function(s) {
    let map = {'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000},
        sum = 0, loop = 0, num = 0, now = 0;
    while(loop < s.length) {
        now = map[s[loop]];
        if(num < now) {
            sum -= num;
        } else {
            sum += num;
        }
        num = now;
        loop++;
    }
    sum += num;
    return sum;
};

密碼解密

小明從老闆那裡拿到了一個密碼錶，說是如果解開密碼錶中的秘密，就可以升職加薪，贏取白富美，走向人生巔峰。這個密碼錶是一個 CSV 文件，裡面的數據由數字（沒有小數點）、字母組成。小明需要提取每個數據中的數字（例如 1a2b3c 提取後得到 123，提取後的數字整體看作一個十進位數），把數值為奇數的項相加，就可以解開這個秘密。請你實現一個函數 sum，幫小明完成這項工作。

function sum(input: string) {

  return input.split(/[,\n]/)

    .map(item => Number(item.replace(/[a-z]/ig, "")))

    .filter(num => num % 2 === 1)

    .reduce((a, b) => a + b)

}

解析url參數為對象

function parseUrl(url){
    url = decodeURIComponent(url);
    let strs = url.slice(url.indexOf('?')+1).split('&');
    return strs.reduce((x,y)=>{
        let key = y.split('=')[0];
        let value = Object.is(Number(y.split('=')[1]),NaN) ? y.split('=')[1] : Number(y.split('=')[1]);
        x[key] = value;
        return x;
    },{});
}

實現模板引擎

const template = 'there are ${count} ${name} on the ${place}.';
function parse(template,obj){
    let reg = /\$\{((\w|_|\$)*)\}/g;
    let keys = template.match(reg).map(x => x.slice(2,x.length-1));
    let value = keys.map(i => obj[i] === undefined ? '' : String(obj[i]));
    return template.replace(reg,()=> value.shift());
}
console.log(parse(template, {count: 2, name: 'apples', place: 'table'}, create));

//there are 2 apples on the table.

寫函數任意標籤轉成json文件

//<div>  <span>     <a></a >  </span>  <span>  <a></a >    <a></a > </span></div>
//{  tag: 'DIV',children: [    {      tag: 'SPAN',    children: [       { tag: 'A', children: [] }      ] },    {     tag: 'SPAN',      children: [        { tag: 'A', children: [] },       { tag: 'A', children: [] }    ]   }  ]}
function Dom2JSON(str) {
	function helper(str) {
    	let reg = /<(.+)>(.*?)<\/\1>/g;
        let result = null;
        let nodes = [];
        while ((result = reg.exec(str)) != null) {
        	let currentNode = createJSON(result[1]);
            nodes.push(currentNode);
            let children = helper(result[2]);
            if (children.length != 0) currentNode.children = children;
       }
       return nodes;
	}
    let result = helper(str);
    result = result.length !== 0 ? result[0] : result;
	return JSON.stringify(result);
}

參考文獻

回溯法套路模板刷通leetcode

八大排序，各顯神通–動圖版

八大排序經典演算法（圖解+參考源程式碼）

Front-End-Interview-Notebook

Tags: 數據結構與演算法