二、基礎數據結構
一、線性結構

1.1、數組
- 一種線性表數據結構。它用一組連續的記憶體空間,來存儲一組具有相同類型的數據。
- 最大的特點就是支援隨機訪問,但插入、刪除操作也因此變得比較低效,平均情況時間複雜度為O(n)。
1、特性:
- 第一是線性表(Linear List)。顧名思義,線性表就是數據排成像一條線一樣的結構。每個線性表上的數據最多只有前和後兩個方向。其實除了數組,鏈表、隊列、棧等也是線性表結構。
- 第二個是連續的記憶體空間和相同類型的數據。正是因為這兩個限制,它才有了一個堪稱「殺手鐧」的特性: 「隨機訪問」。但有利就有弊,這兩個限制也讓數組的很多操作變得非常低效,比如要想在數組中刪除、插入一個數據,為了保證連續性,就需要做大量的數據搬移工作。
例子:
我們拿一個長度為 10 的 int 類型的數組 int[] a = new int[10] 來舉例。在我畫的這個圖中,電腦給數組 a[10],分配了一塊連續記憶體空間 1000~ 1039,其中,記憶體塊的首地址為 base_address = 1000。

- 我們知道,電腦會給每個記憶體單元分配一個地址,電腦通過地址來訪問記憶體中的數據。
- 當電腦需要隨機訪問數組中的某個元素時,它會首先通過下面的定址公式,計算出該元素存儲的記憶體地址:
- a[i]_address = base_address + i * data_type_size
- 其中 data_type_size 表示數組中每個元素的大小。我們舉的這個例子里,數組中存儲的是 int 類型數據,所以 data_type_size 就為 4 個位元組。
- 數組支援隨機訪問,根據下標隨機訪問的時間複雜度為O(1)。
2、低效的「插入」和「刪除」
插入操作:
- 假設數組的長度為 n,現在,如果我們需要將一個數據插入到數組中的第 k 個位置。為了把第 k 個位置騰出來,給新來的數據,我們需要將第 k ~ n 這部分的元素都順序地往後挪一位。
- 如果在數組的末尾插入元素,那就不需要移動數據了,這時的時間複雜度為 O(1)。但如果在數組的開頭插入元素,那所有的數據都需要依次往後移動一位,所以最壞時間複雜度是 O(n)。 因為我們在每個位置插入元素的概率是一樣的,所以平均情況時間複雜度為 (1+2+…n)/n=O(n)。
- 如果數組中的數據是有序的,我們在某個位置插入一個新的元素時,就必須按照剛才的方法搬移 k 之後的數據。但是,如果數組中存儲的數據並沒有任何規律,數組只是被當作一個存儲數據的集合。在這種情況下,如果要將某個數組插入到第 k 個位置,為了避免大規模的數據搬移,我們還有一個簡單的辦法就是,直接將第 k 位的數據搬移到數組元素的最後,把新的元素直接放入第k個位置。
- 為了更好地理解,舉一個例子。假設數組 a[10] 中存儲了如下 5 個元素: a, b, c, d, e。我們現在需要將元素 x 插入到第3個位置。我們只需要將 c 放入到 a[5],將 a[2] 賦值為 x 即可。最後,數組中的元素如下: a, b, x, d, e, c。
-
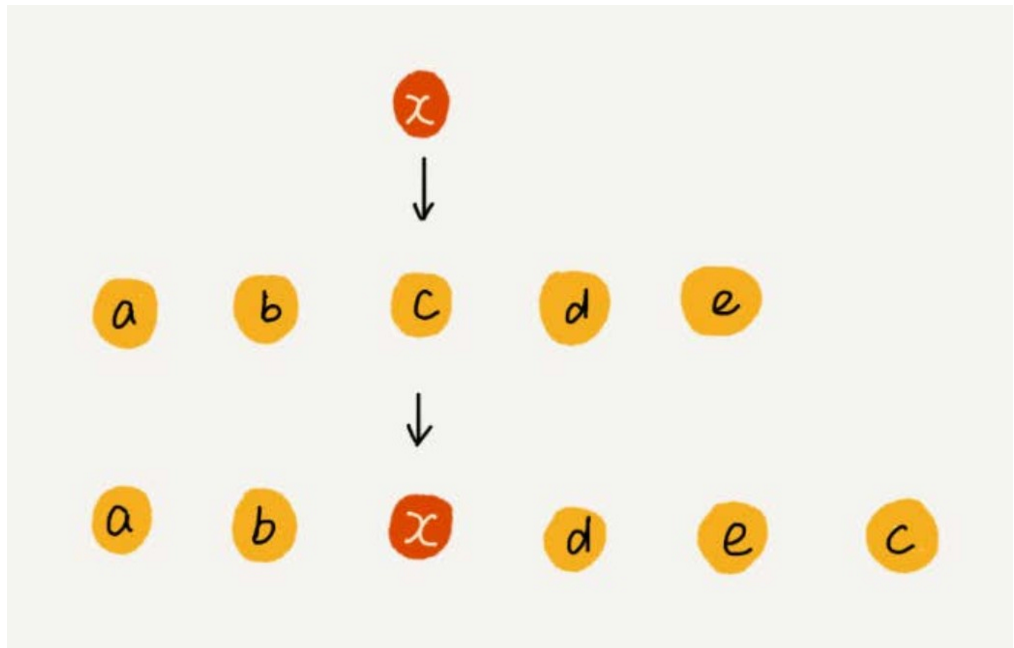
利用這種處理技巧,在特定場景下,在第 k 個位置插入一個元素的時間複雜度就會降為 O(1)。這個處理思想在快排中也會用到。
刪除操作:
-
跟插入數據類似,如果我們要刪除第 k 個位置的數據,為了記憶體的連續性,也需要搬移數據,不然中間就會出現空洞,記憶體就不連續了。
-
和插入類似,如果刪除數組末尾的數據,則最好情況時間複雜度為 O(1);如果刪除開頭的數據,則最壞情況時間複雜度為 O(n);平均情況時間複雜度也為 O(n)。
-
實際上,在某些特殊場景下,我們並不一定非得追求數組中數據的連續性。如果我們將多次刪除操作集中在一起執行,刪除的效率是不是會提高很多呢?
-
我們繼續來看例子。數組 a[10] 中存儲了 8 個元素:a, b, c, d, e, f, g, h。現在,我們要依次刪除 a, b, c 三個元素。
-
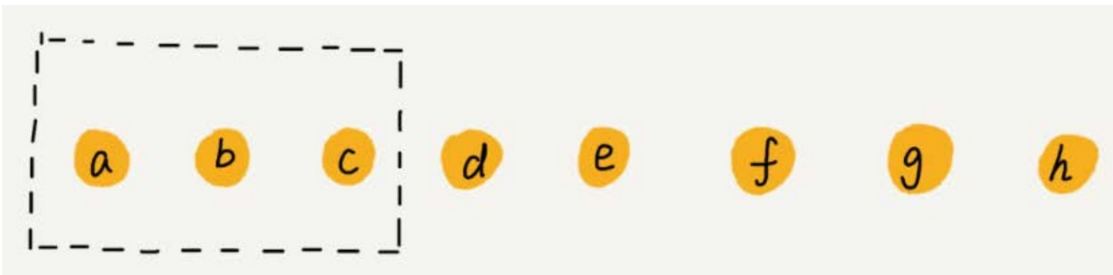
-
為了避免 d, e, f, g, h 這幾個數據會被搬移三次,我們可以先記錄下已經刪除的數據。
-
每次的刪除操作並不是真正地搬移數據,只是記錄數據已經被刪除。
-
當數組沒有更多空間存儲數據時,我們再觸發執行一次真正的刪除操作,這樣就大大減少了刪除操作導致的數據搬移。
-
如果你了解 JVM,你會發現,這不就是 JVM 標記清除垃圾回收演算法的核心思想嗎?
3、容器(集合類:ArrayList)能否完全替代數組?
- 針對數組類型,很多語言都提供了容器類,比如 Java 中的 ArrayList、 C++ STL 中的 vector。
- ArrayList 的優勢:
- 可以將很多數組操作的細節封裝起來。比如前面提到的數組插入、刪除數據時需要搬移其他數據等。
- 支援動態擴容。數組本身在定義的時候需要預先指定大小,因為需要分配連續的記憶體空間。如果我們申請了大小為10的數組,當第11個數據需要存儲到數組中時,我們就需要重新分配一塊更大的空間,將原來的數據複製過去,然後再將新的數據插入。
- 如果使用ArrayList,我們就完全不需要關心底層的擴容邏輯, ArrayList已經幫我們實現好了。每次存儲空間不夠的時候,它都會將空間自動擴容為1.5倍大小。不過,這裡需要注意一點,因為擴容操作涉及記憶體申請和數據搬移,是比較耗時的。所以,如果事先能確定需要存儲的數據大小,最好在創建 ArrayList 的時候事先指定數據大小。
- 比如我們要從資料庫中取出 10000 條數據放入 ArrayList。事先指定數據大小可以省掉很多次記憶體申請和數據搬移操作。
數組和 ArrayList 的選擇:
- Java ArrayList 無法存儲基本類型,比如 int、 long,需要封裝為 Integer、 Long 類,而 Autoboxing、 Unboxing 則有一定的性能消耗,所以如果特別關注性能,或者希望使用基本類型,就可以選用數組。
- 如果數據大小事先已知,並且對數據的操作非常簡單,用不到 ArrayList 提供的大部分方法,也可以直接使用數組。
- 當要表示多維數組時,用數組往往會更加直觀。比如 Object[][] array;而用容器的話則需要這樣定義: ArrayList
array。 - 總結一下,對於業務開發,直接使用容器就足夠了,省時省力。畢竟損耗一丟丟性能,完全不會影響到系統整體的性能。但如果是做一些非常底層的開發,比如開發網路框架,性能的優化需要做到極致,這個時候數組就會優於容器,成為首選。
4、數組要從0開始編號,而不是從1開始呢?
- 從數組存儲的記憶體模型上來看, 「下標」最確切的定義應該是「偏移(offset) 」。
- 前面也提到,如果用 a 來表示數組的首地址, a[0] 就是偏移為 0 的位置,也就是首地址,a[k] 就表示偏移 k 個 type_size 的位置,所以計算 a[k] 的記憶體地址只需要用這個公式:
- a[k]_address = base_address + k * type_size
- 但是,如果數組從1開始計數,那我們計算數組元素a[k]的記憶體地址就會變為:
- a[k]_address = base_address + (k-1)*type_size
- 對比兩個公式,我們不難發現,從1開始編號,每次隨機訪問數組元素都多了一次減法運算,對於 CPU 來說,就是多了一次減法指令。
- 數組作為非常基礎的數據結構,通過下標隨機訪問數組元素又是其非常基礎的編程操作,效率的優化就要儘可能做到極致。
- 所以為了減少一次減法操作,數組選擇了從0開始編號,而不是從1開始。
1.2、鏈表
1、對比數組
底層的存儲結構:
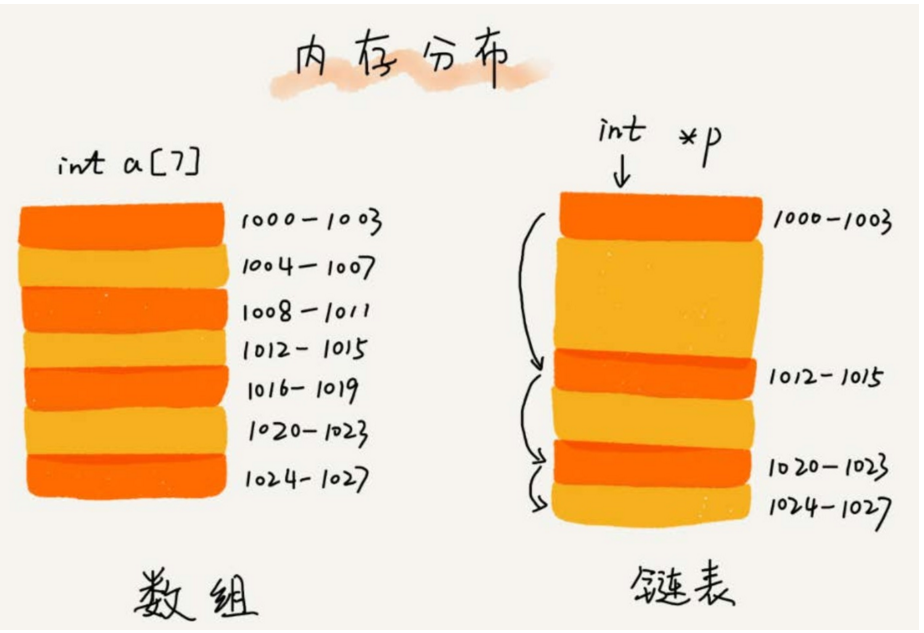
- 為了直觀地對比,我畫了一張圖。從圖中我們看到,數組需要一塊連續的記憶體空間來存儲,對記憶體的要求比較高。如果我們申請一個 100MB 大小的數組,當記憶體中沒有連續的、足夠大的存儲空間時,即便記憶體的剩餘總可用空間大於 100MB,仍然會申請失敗。
- 而鏈表恰恰相反,它並不需要一塊連續的記憶體空間,它通過「指針」將一組零散的記憶體塊串聯起來使用,所以如果我們申請的是 100MB 大小的鏈表,根本不會有問題。
-
性能比較:

總結來看:
- 數組簡單易用,在實現上使用的是連續的記憶體空間,可以藉助CPU的快取機制,預讀數組中的數據,所以訪問效率更高。而鏈表在記憶體中並不是連續存儲,所以對CPU快取不友好,沒辦法有效預讀。
- 數組的缺點是大小固定,一經聲明就要佔用整塊連續記憶體空間。如果聲明的數組過大,系統可能沒有足夠的連續記憶體空間分配給它,導致「記憶體不足(out ofmemory) 」。如果聲明的數組過小,則可能出現不夠用的情況。這時只能再申請一個更大的記憶體空間,把原數組拷貝進去,非常費時。鏈表本身沒有大小的限制,天然地支援動態擴容。
- 你可能會說,我們 Java 中的 ArrayList 容器,也可以支援動態擴容啊?我們上一節課講過,當我們往支援動態擴容的數組中插入一個數據時,如果數組中沒有空閑空間了,就會申請一個更大的空間,將數據拷貝過去,而數據拷貝的操作是非常耗時的。我舉一個稍微極端的例子。如果我們用 ArrayList 存儲了了 1GB 大小的數據,這個時候已經沒有空閑空間了,當我們再插入數據的時候, ArrayList 會申請一個 1.5GB 大小的存儲空間,並且把原來那1GB的數據拷貝到新申請的空間上。聽起來是不是就很耗時?
- 除此之外,如果你的程式碼對記憶體的使用非常苛刻,那數組就更適合你。因為鏈表中的每個結點都需要消耗額外的存儲空間去存儲一份指向下一個結點的指針,所以記憶體消耗會翻倍。而且,對鏈表進行頻繁的插入、刪除操作,還會導致頻繁的記憶體申請和釋放,容易造成記憶體碎片,如果是Java語言,就有可能會導致頻繁的GC(Garbage Collection,垃圾回收)。
- 所以,在我們實際的開發中,針對不同類型的項目,要根據具體情況,權衡究竟是選擇數組還是鏈表。
2、單向鏈表
-
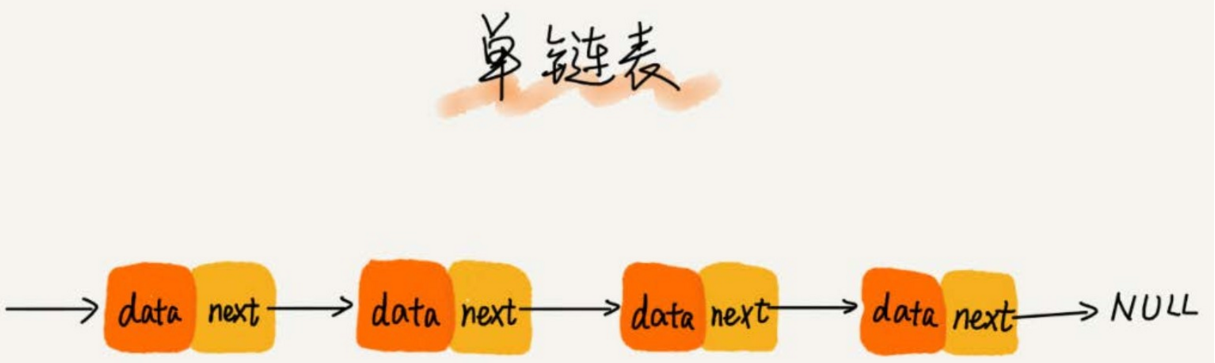
鏈表通過指針將一組零散的記憶體塊串聯在一起。其中,我們把記憶體塊稱為鏈表的「結點」。
-
為了將所有的結點串起來,每個鏈表的結點除了存儲數據之外,還需要記錄鏈上的下一個結點的地址。
-
如下圖所示,我們把這個記錄下個結點地址的指針叫作後繼指針 next。
-
-
從圖中可以發現,其中有兩個結點是比較特殊的,它們分別是第一個結點和最後一個結點。
-
第一個結點叫作頭結點,頭結點用來記錄鏈表的基地址。有了它,我們就可以遍歷得到整條鏈表。
-
把最後一個結點叫作尾結點。而尾結點特殊的地方是:指針不是指向下一個結點,而是指向一個空地址NULL,表示這是鏈表上最後一個結點。
插入、修改、查找
-
與數組一樣,鏈表也支援數據的查找、插入和刪除操作。我們知道,在進行數組的插入、刪除操作時,為了保持記憶體數據的連續性,需要做大量的數據搬移,所以時間複雜度是O(n)。
-
在鏈表中插入或者刪除一個數據,我們並不需要為了保持記憶體的連續性而搬移結點,因為鏈表的存儲空間本身就不是連續的。
-
所以,在鏈表中插入和刪除一個數據是非常快速的。從下圖中我們可以看出,針對鏈表的插入和刪除操作,我們只需要考慮相鄰結點的指針改變,所以對應的時間複雜度是O(1)。
-
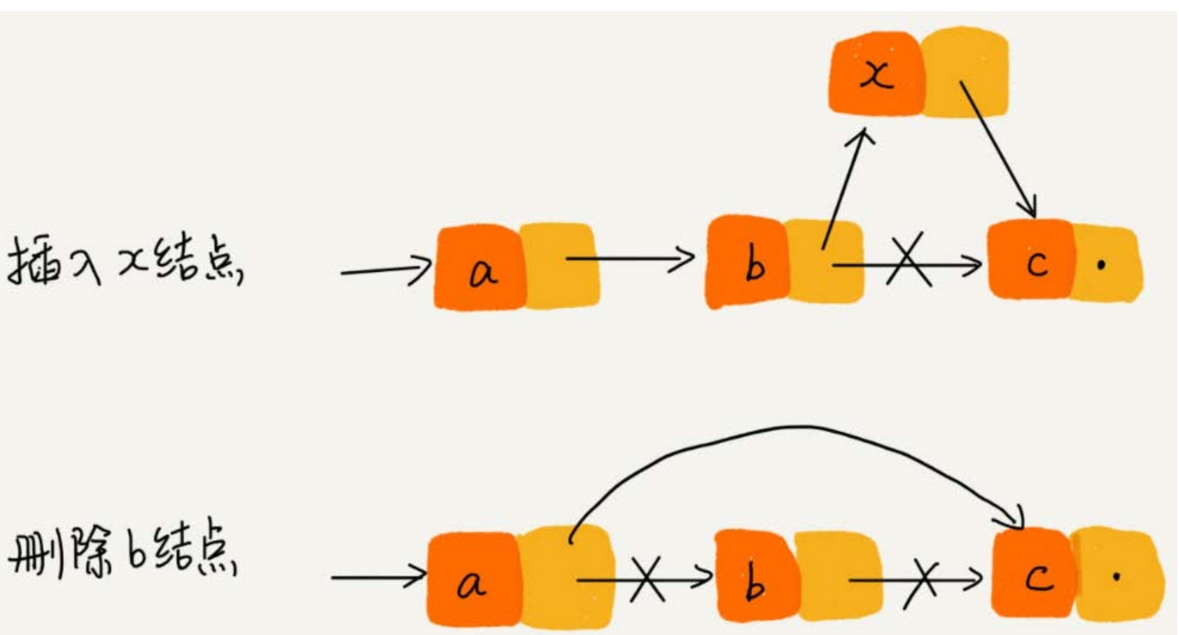
-
鏈表要想隨機訪問第k個元素,就沒有數組那麼高效了。因為鏈表中的數據並非連續存儲的,所以無法像數組那樣,根據首地址和下標,通過定址公式就能直接計算出對應的記憶體地址,而是需要根據指針一個結點一個結點地依次遍歷,直到找到相應的結點。
-
所以,鏈表隨機訪問的性能沒有數組好,需要 O(n) 的時間複雜度。
3、循環鏈表
-
循環鏈表是一種特殊的單鏈表。
-
它跟單鏈表唯一的區別就在尾結點。我們知道,單鏈表的尾結點指針指向空地址,表示這就是最後的結點了。
-
而循環鏈表的尾結點指針是指向鏈表的頭結點。如下圖所示,它像一個環一樣首尾相連,所以叫作「循環」鏈表。
-
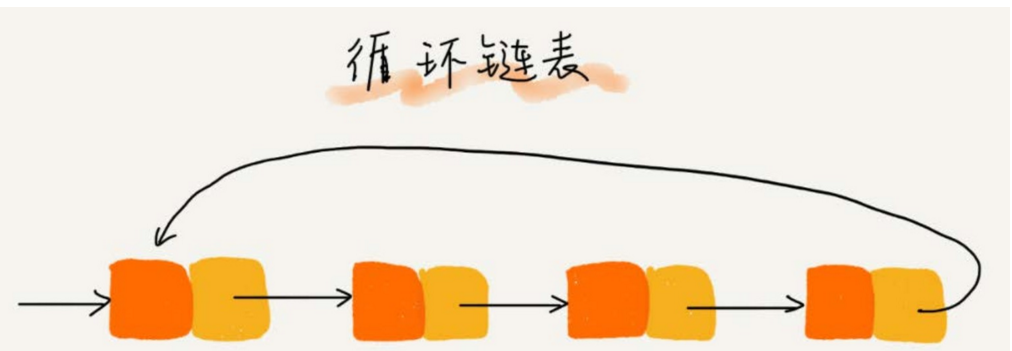
-
和單鏈表相比, 循環鏈表的優點是從鏈尾到鏈頭比較方便。
-
當要處理的數據具有環型結構特點時,就特別適合採用循環鏈表。
4、雙向鏈表。
-
單向鏈表只有一個方向,結點只有一個後繼指針 next 指向後面的結點。而雙向鏈表,顧名思義,它支援兩個方向,每個結點不止有一個後繼指針 next 指向後面的結點,還有一個前驅指針 prev 指向前面的結點。
-
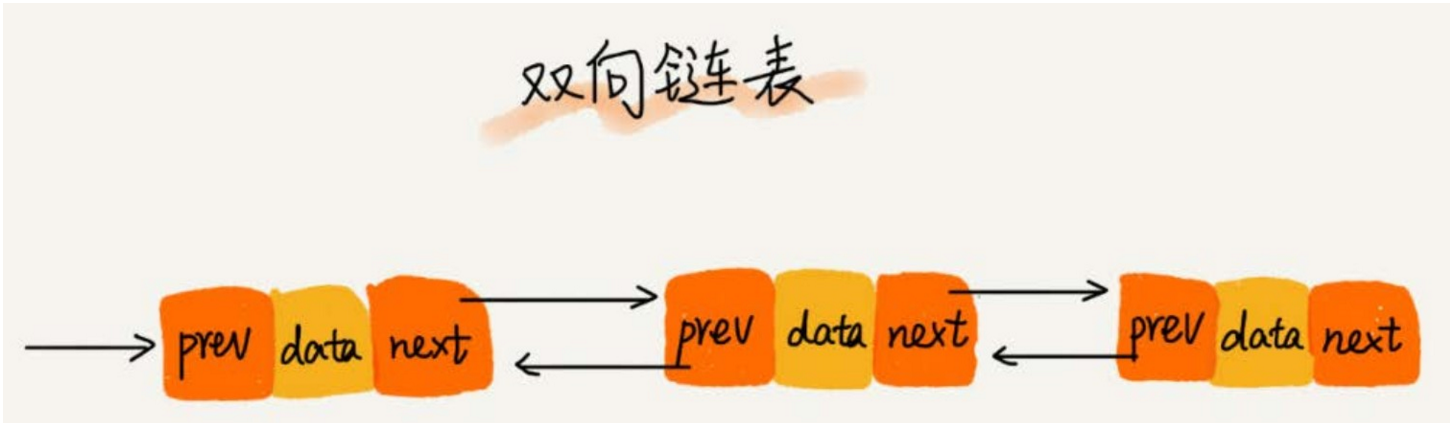
-
雙向鏈表需要額外的兩個空間來存儲後繼結點和前驅結點的地址。所以,如果存儲同樣多的數據,雙向鏈表要比單鏈表佔用更多的記憶體空間。
-
雖然兩個指針比較浪費存儲空間,但可以支援雙向遍歷,這樣也帶來了雙向鏈表操作的靈活性。那相比單鏈表,雙向鏈表適合解決哪種問題呢?
-
從結構上來看,雙向鏈表可以支援 O(1) 時間複雜度的情況下找到前驅結點,正是這樣的特點,也使雙向鏈表在某些情況下的插入、刪除等操作都要比單鏈表簡單、高效。
舉個刪除的例子:
-
刪除結點中「值等於某個給定值」的結點:
- 對於這種情況,不管是單鏈表還是雙向鏈表,為了查找到值等於給定值的結點,都需要從頭結點開始一個一個依次遍歷對比,直到找到值等於給定值的結點,然後再通過我前面講的指針操作將其刪除。
- 儘管單純的刪除操作時間複雜度是O(1),但遍歷查找的時間是主要的耗時點,對應的時間複雜度為O(n)。根據時間複雜度分析中的加法法則,刪除值等於給定值的結點對應的鏈表操作的總時間複雜度為O(n)。
-
刪除給定指針指向的結點:
- 對於第二種情況,我們已經找到了要刪除的結點,但是刪除某個結點 q 需要知道其前驅結點,而單鏈表並不支援直接獲取前驅結點,所以,為了找到前驅結點,我們還是要從頭結點開始遍歷鏈表,直到 p -> next = q,說明 p 是 q 的前驅結點。
- 但是對於雙向鏈表來說,這種情況就比較有優勢了。因為雙向鏈表中的結點已經保存了前驅結點的指針,不需要像單鏈表那樣遍歷。所以,針對第二種情況,單鏈表刪除操作需要 O(n) 的時間複雜度,而雙向鏈表只需要在 O(1) 的時間複雜度內就搞定了!
- 同理,如果我們希望在鏈表的某個指定結點前面插入一個結點,雙向鏈表比單鏈表有很大的優勢。雙向鏈表可以在 O(1) 時間複雜度搞定,而單向鏈表需要 O(n) 的時間複雜度。
-
除了插入、刪除操作有優勢之外,對於一個有序鏈表,雙向鏈表的按值查詢的效率也要比單鏈表高一些。因為,我們可以記錄上次查找的位置 p,每次查詢時,根據要查找的值與 p 的大小關係,決定是往前還是往後查找,所以平均只需要查找一半的數據。
-
這就是為什麼在實際的軟體開發中,雙向鏈表儘管比較費記憶體,但還是比單鏈表的應用更加廣泛的原因。
-
如果你熟悉Java語言,你肯定用過LinkedHashMap這個容器。如果你深入研究LinkedHashMap的實現原理,就會發現其中就用到了雙向鏈表這種數據結構。
-
實際上,這裡有一個更加重要的知識點需要你掌握,那就是用空間換時間的設計思想。當記憶體空間充足的時候,如果我們更加追求程式碼的執行速度,我們就可以選擇空間複雜度相對較高、但時間複雜度相對很低的演算法或者數據結構。相反,如果記憶體比較緊缺,比如程式碼跑在手機或者單片機上,這個時候,就要反過來用時間換空間的設計思路。
1.3、棧
從棧的操作特性上來看, 棧是一種「操作受限」的線性表,只允許在一端插入和刪除數據。先進後出。
/**
* @author xiandongxie
* 基於數組實現的棧
*/
public class ArrayStack {
public String[] arr = null;
private int num;//棧中元素個數
private int n;// 棧的大小
public ArrayStack(int n) {
arr = new String[n];
num = 0;
this.n = n;
}
public boolean push(String value) {
if (StringUtils.isEmpty(value)) return false;
if (num >= n) return false;
arr[num] = value;
num++;
return true;
}
public String pop() {
if (num > n || num <= 0) return null;
num--;
return arr[num];
}
}
1.4、隊列
隊列跟棧一樣,也是一種操作受限的線性表數據結構。只不過可以再兩端操作,先進先出。
1、單列隊列
隊列的概念很好理解,基本操作也很容易掌握。作為一種非常基礎的數據結構,隊列的應用也非常廣泛,特別是一些具有某些額外特性的隊列,比如循環隊列、阻塞隊列、並發隊列。它們在很多偏底層系統、框架、中間件的開發中,起著關鍵性的作用。比如高性能隊列 Disruptor、 Linux 環形快取,都用到了循環並發隊列; Java concurrent 並發包利用 ArrayBlockingQueue 來實現公平鎖等。
/**
* 用數組實現隊列
*/
class ArrayQueue {
// 裝載數據的數組
private String[] arr;
// 數組容量大小
private int n;
// 隊列頭
private int start;
// 隊列尾
private int end;
public ArrayQueue(int n) {
this.arr = new String[n];
this.start = 0;
this.end = 0;
this.n = n;
}
// 添加元素
public boolean push(String data) throws Exception {
if (end >= n && start == 0) {
throw new Exception("超出容量,且數據不需要移動,此時只能對隊列擴容才能存入," +
"end=" + end + ", n=" + n + ", start=" + start);
}
if (end >= n && start > 0) {
System.out.println("超出容量,但是隊列頭部已經消費,可以移動數據擴容," +
"end=" + end + ", n=" + n + ", start=" + start);
for (int i = 0; i < end - start; i++) {
arr[i] = arr[start + i];
}
end = end - start;
start = 0;
}
arr[end] = data;
end++;
return true;
}
// 取出元素
public String pop() throws Exception {
if (end <= 0 || start >= end) {
throw new Exception("沒有元素,隊列為空,end=" + end + ", n=" + n + ", start=" + start);
}
String value = arr[start];
start++;
return value;
}
public String[] getArr() {
return arr;
}
}
/**
* 用鏈表實現隊列
*/
class LinkedQueue {
// 定義節點類
private class Node {
Node nextNode;
String value;
}
// 頭指針
private Node head;
// 尾指針
private Node tail;
// 數據個數
private int size;
public LinkedQueue() {
this.size = 0;
}
// 添加
public boolean push(String data) {
Node newNode = new Node();
newNode.value = data;
if (size == 0) {
head = newNode;
} else {
tail.nextNode = newNode;
}
tail = newNode;
size++;
return true;
}
// 移除
public String pop() throws Exception {
if (size <= 0) {
throw new Exception("隊列為空,size=" + size);
}
if (size == 1){
tail = null;
}
size--;
String value = head.value;
head = head.nextNode;
return value;
}
}
-
對於棧來說,我們只需要一個棧頂指針就可以了。
-
但是隊列需要兩個指針:一個是 head 指針,指向隊頭;一個是 tail 指針,指向隊尾。
-
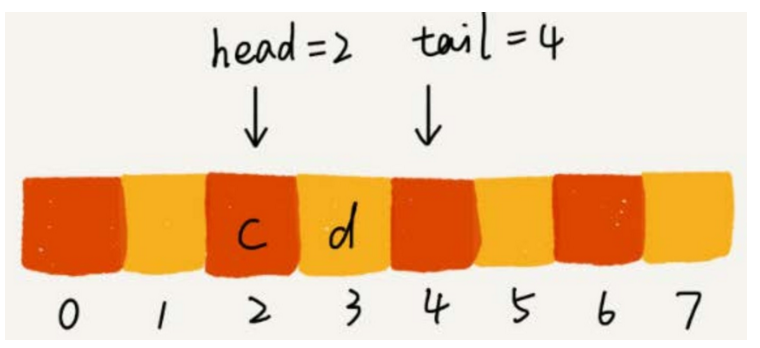
你可以結合下面這幅圖來理解。當 a 、b、c、d 依次入隊之後,隊列中的 head 指針指向下標為 0 的位置, tail 指針指向下標為 4 的位置。
-
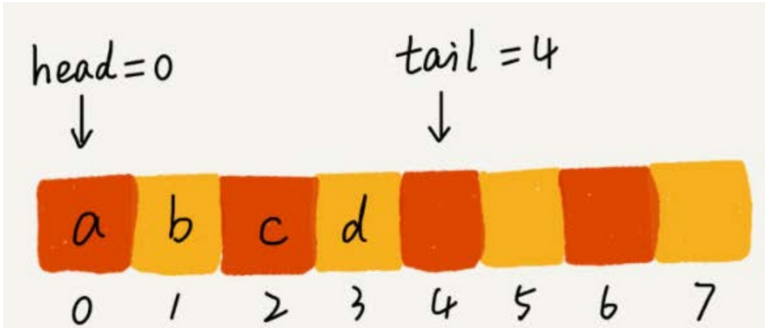
-
當我們調用兩次出隊操作之後,隊列中 head 指針指向下標為 2 的位置, tail 指針仍然指向下標為4的位置。
-
-
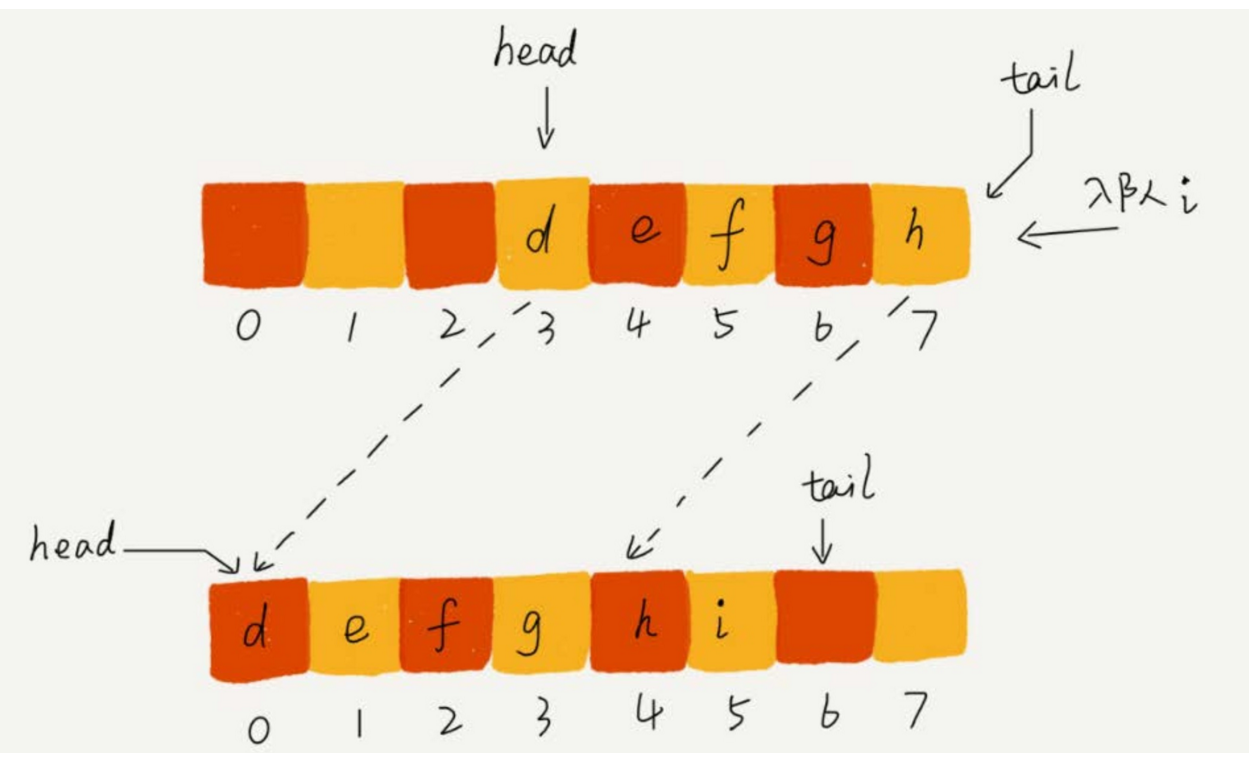
隨著不停地進行入隊、出隊操作, head 和 tail 都會持續往後移動。當 tail 移動到最右邊,即使數組中還有空閑空間,也無法繼續往隊列中添加數據了。這個問題該如何解決呢?
-
用數據搬移!但是,每次進行出隊操作都相當於刪除數組下標為 0 的數據,要搬移整個隊列中的數據,這樣出隊操作的時間複雜度就會從原來的 O(1) 變為 O(n)。能不能優化一下呢?
-
我們在出隊時可以不用搬移數據。如果沒有空閑空間了,我們只需要在入隊時,再集中觸發一次數據的搬移操作。藉助這個思想,出隊函數 pop() 保持不變,我們稍加改造一下入隊函數 push() 的實現,就可以輕鬆解決剛才的問題了。
-
2、循環隊列
-
我們剛才用數組來實現隊列的時候,在 tail == n 時,會有數據搬移操作,這樣入隊操作性能就會受到影響。那有沒有辦法能夠避免數據搬移呢?
-
我們來看看循環隊列的解決思路。循環隊列,顧名思義,它長得像一個環。原本數組是有頭有尾的,是一條直線。現在我們把首尾相連,扳成了一個環。
-
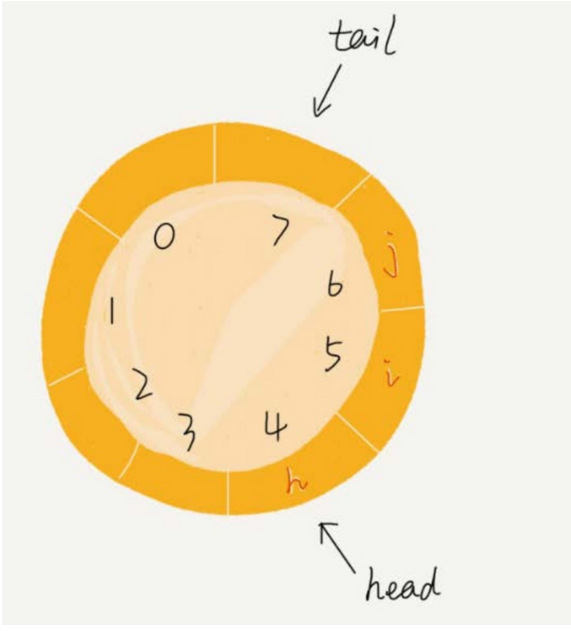
-
我們可以看到,圖中這個隊列的大小為 8,當前 head=4, tail=7。當有一個新的元素 a 入隊時,我們放入下標為 7 的位置。
-
但這個時候,我們並不把 tail 更新為8,而是將其在環中後移一位,到下標為 0 的位置。
-
當再有一個元素 b 入隊時,我們將 b 放入下標為 0 的位置,然後 tail 加 1 更新為 1。
-
所以,在 a, b 依次入隊之後,循環隊列中的元素就變成了下面的樣子:
-
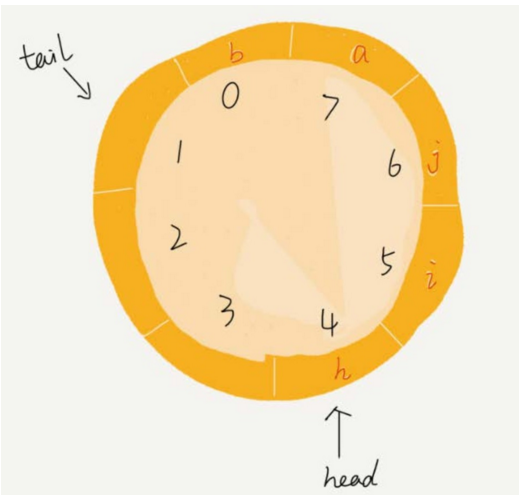
-
通過這樣的方法,我們成功避免了數據搬移操作。
-
看起來不難理解,但是循環隊列的程式碼實現難度要比前面講的非循環隊列難多了。要想寫出沒有bug的循環隊列的實現程式碼,我個人覺得,最關鍵的是,確定好隊空和隊滿的判定條件。
-
在用數組實現的非循環隊列中,隊滿的判斷條件是 tail == n,隊空的判斷條件是 head == tail。
-
循環隊列,隊列為空的判斷條件仍然是 head == tail。但隊列滿的判斷條件就稍微有點複雜了。我畫了一張隊列滿的圖,你可以看一下,試著總結一下規律。
-
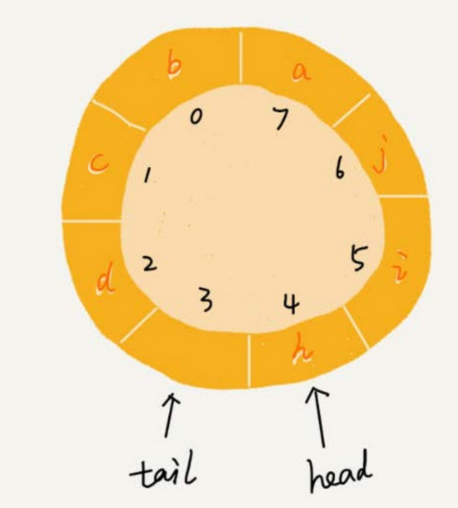
-
就像我圖中畫的隊滿的情況,tail=3,head=4,n=8,所以總結一下規律就是:(3+1) % 8 = 4。多畫幾張隊滿的圖,你就會發現,當隊滿時,(tail+1) % n = head。
-
還有一點是當隊列滿時,圖中的 tail 指向的位置實際上是沒有存儲數據的。所以,循環隊列會浪費一個數組的存儲空間。
public class CircularQueue {
// 數組: items,數組大小: n
private String[] items;
private int n = 0;
// head表示隊頭下標, tail表示隊尾下標
private int head = 0;
private int tail = 0;
// 申請一個大小為capacity的數組
public CircularQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
// 入隊
public boolean enqueue(String item) {
// 隊列滿了
if ((tail + 1) % n == head)
return false;
items[tail] = item;
tail = (tail + 1) % n;
return true;
}
// 出隊
public String dequeue() {
// 如果head == tail 表示隊列為空
if (head == tail)
return null;
String ret = items[head];
head = (head + 1) % n;
return ret;
}
}
3、阻塞隊列和並發隊列
-
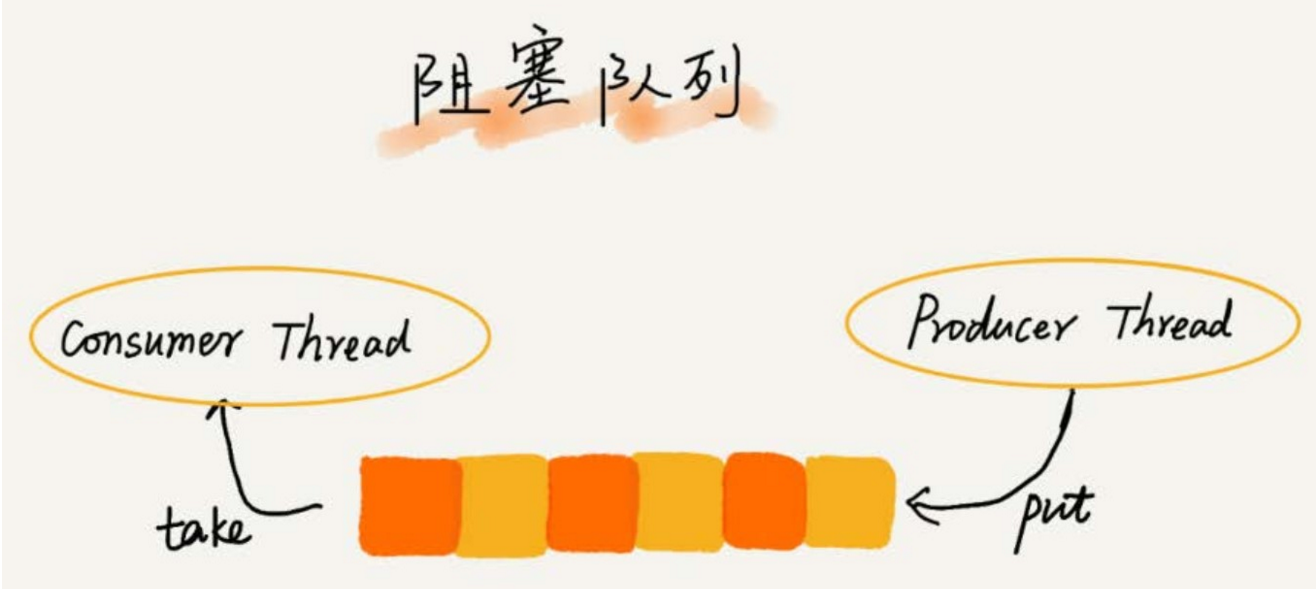
阻塞隊列其實就是在隊列基礎上增加了阻塞操作。
-
簡單來說,就是在隊列為空的時候,從隊頭取數據會被阻塞。因為此時還沒有數據可取,直到隊列中有了數據才能返回;
-
如果隊列已經滿了,那麼插入數據的操作就會被阻塞,直到隊列中有空閑位置後再插入數據,然後再返回。
-
上述的定義就是一個「生產者-消費者模型」!我們可以使用阻塞隊列,輕鬆實現一個「生產者-消費者模型」!
-
這種基於阻塞隊列實現的「生產者-消費者模型」,可以有效地協調生產和消費的速度。
-
當「生產者」生產數據的速度過快,「消費者」來不及消費時,存儲數據的隊列很快就會滿了。這個時候,生產者就阻塞等待,直到「消費者」消費了數據, 「生產者」才會被喚醒繼續「生產」。
-
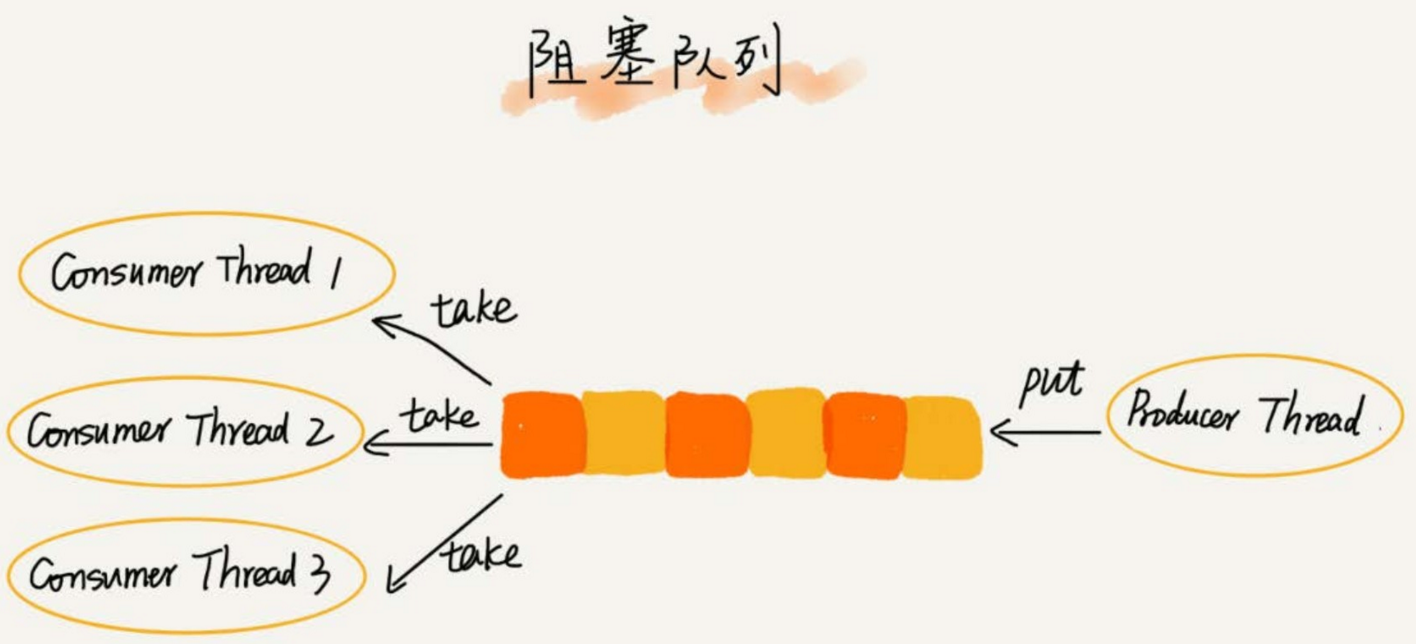
而且不僅如此,基於阻塞隊列,我們還可以通過協調「生產者」和「消費者」的個數,來提高數據的處理效率。比如前面的例子,我們可以多配置幾個「消費者」,來應對一個「生產者」。
-
阻塞隊列,在多執行緒情況下,會有多個執行緒同時操作隊列,這個時候就會存在執行緒安全問題,那如何實現一個執行緒安全的隊列呢?
-
執行緒安全的隊列我們叫作並發隊列。最簡單直接的實現方式是直接在 enqueue()、 dequeue() 方法上加鎖,但是鎖粒度大並發度會比較低,同一時刻僅允許一個存或者取操作。
-
實際上,基於數組的循環隊列,利用 CAS 原子操作,可以實現非常高效的並發隊列。這也是循環隊列比鏈式隊列應用更加廣泛的原因。

















