電腦組成原理
電腦發展史(四個階段)
第一階段(1946~1957):電子管電腦
世界上第一台電腦叫埃尼阿克(ENIAC)

第二次世界大戰是電子管電腦產生的催化劑(英國為了解密德國海軍的密文),在第二次世界大戰中,戰爭使用了飛機和火箭,打得准需要計算設計參數,設計參數需要幾千次運算才能計算出來,在沒有電腦之前 ,這些都需要人工手動去計算,埃尼阿克的計算速度大約是手工計算的20萬倍。
埃尼阿克(ENIAC)由18000多個電子管,運行耗電量達150千瓦,重量達30噸,佔地1500平方英尺。由此可見,第一階段的電子管電腦,集成度小,空間佔用大,功耗高,運行速度慢,操作複雜,更換程式需要接線。
第二階段(1957~1964):電晶體電腦
貝爾實驗室的三個科學家發明了電晶體,第一台電晶體電腦產生於麻省理工大學的林肯實驗室。

第三階段(1964~1980):積體電路電腦
德州儀器的工程師發明了積體電路(IC),後面就有了積體電路電腦,積體電路電腦讓電腦具備進入千家萬戶的條件。因為積體電路使電腦變得更小,功耗變得更低,計算速度變得更快。

關於積體電路電腦,IBM當時主要推出了兩款電腦,使用量比較大,分別是7094和1401,但這兩款電腦的主打功能不同,而且相互無法兼容,公司也不願意投入兩組人力,於時後來IBM推出了兼容的產品System/360,這也是作業系統的雛形。
第四階段(1980~至今):超大規模積體電路電腦

超大規模積體電路,一個晶片上集成了上百萬的電晶體,這樣使超大規模積體電路電腦速度更快,價格更低,體積更小,更能被大眾所接受,而且用途豐富,可以用作文本處理,表格處理,高交互的由於與應用等。
電腦的分類
超級電腦
功能最強、運算速度最快、存儲容量最大的電腦,多用於國家高科技領域和尖端技術研究。
運算速度單位是TFlop/s,1TFlob/s=每秒一萬億次浮點數計算
大型電腦
大型電腦又稱大型機、大型主機、主機等;具有高性能,可處理大數據與複雜的運算;在大型機市場領域,IBM佔據著很大的份額。

去”IOE”行動,”IOE”是分別指IBM,Oracle,EMC,去”IOE”是阿里巴巴提出的概念,代表了高維護費用的存儲系統,不夠靈活,伸縮性弱。阿里巴巴在2008年提出去「IOE」行動,在2009年成立了阿里雲。
迷你電腦(伺服器)
迷你電腦也稱為小型機,即普通伺服器,不需要特殊的空調場所,具備不錯的算力,可以完成較複雜的運算。普通的伺服器已經替代了傳統的大型機,成為大規模企業計算的中樞。
工作站
高端的通用微型電腦,提供比個人電腦更強大的性能,類似於普通台式電腦,體積較大,但性能較強。

微型電腦
微型電腦又稱為個人電腦,是最普通的一類電腦。麻雀雖小,五臟俱全,從構成的體質上來講,個人電腦與前面的分類的無異。

電腦的體系與結構
馮諾依曼體系
馮諾依曼體系:將程式指令和數據一起存儲的電腦設計概念結構。在馮諾依曼體系出現前,早期的電腦僅含固定用途程式,如改變程式就需要更改結構,重新設計電路,也就是不能先打會兒遊戲然後再寫會兒程式碼,這樣就很影響我們的使用體驗,所以就提出將程式存儲起來,並設計成通用電路,即存儲程式指令,設計通用電路。
馮諾依曼體系提出:電腦必須有一個存儲器、有一個控制器、有一個計算器、有輸入設備和輸出設備。這樣就能夠把需要的程式和數據送至電腦中(輸入設備),能夠長期記憶程式、數據、中間結果及最終運算結果的能力(存儲器),能夠具備算術、邏輯運算和數據傳送等數據加工處理的能力(運算器、控制器),能夠按照要求將處理結果輸出給用戶(輸出設備)。

由於CPU處理數據的速度要遠快於存儲器的存儲速度,所以CPU和存儲器的分開會造成芬諾伊曼瓶頸,也就是CPU和存儲器之間的速率問題無法調和。

現代電腦的結構
現代電腦在馮諾曼體系結構基礎上進行修改,解決CPU與存儲設備之間的性能差異問題。

電腦的層次與程式語言
程式翻譯與程式解釋
我們將人類語言變為電腦能看懂的語言,需要進行語言之間的轉換。程式翻譯就是將較為高級的電腦語言L1轉為較為低級的電腦語言L0(編譯器),L0就是電腦實際執行的語言。程式解釋就是把較為高級的語言L1,作為用L0語言實現的一個程式的輸入,然後得到較為低級電腦語言L0。
程式翻譯與程式解釋的對比:
- 電腦實際執行的指令都是L0
- 翻譯過程生成新的L0程式,解釋過程不生成新的L0程式
- 解釋過程由L0編寫解釋器去執行L1程式
程式翻譯的常見語言:C/C++, Object-C, Golang; 程式解釋的常見語言:Python, Php, JavaScript。而Java和C#是屬於翻譯加解釋性語言,Java程式轉為JVM位元組碼的過程是程式翻譯,由JVM位元組碼變成機器碼的過程是程式解釋。
電腦的層次

硬體邏輯層:門、觸發器等邏輯電路組成,屬於電子工程領域。
微程式機器層:程式語言是微指令集,微指令所組成的微程式直接交由硬體執行。
傳統機器層:程式語言是CPU指令集(機器指令),程式語言和硬體直接相關,不同架構的CPU使用不同的指令集。一條機器指令對應一個微程式,一個微程式對應一組機器指令。
作業系統層:向上提供了簡易的操作介面,向下對接了指令系統,管理硬體資源,作業系統層是硬體和軟體之間的適配層。
彙編語言層:程式語言是彙編語言,彙編語言可以翻譯成可直接執行的機器語言,完成翻譯過程的程式就叫彙編器。
高級語言層:程式語言為廣大程式設計師所接受的高級語言,高級語言的種類非常多,有幾百種,常見的高級語言有C/C++、Java、Python、Golang等。
應用層:滿足電腦針對某種用途而專門設計,例如常見的辦公軟體Excel,Word,PPT等。
電腦的字元與編碼集
使用7個bits就可以完全表示ASCII碼,包含95個可列印字元,33個不可列印字元(包括控制字元),即 33+95=128=27,但是這個ASCII碼在很多應用和很多國家中的符號都無法表示,例如數學符號:「\(\div\) \(\neq\) \(\geq\) \(\approx\) \(\pi\)」。所以在第一次對ASCII碼進行擴充時,7bits=> 8bits,在可拓展的ASCII碼中,包含了常見的運算符,帶音標的歐洲字元,和其他常用符、表格等。
字元編碼集的國際化:由於歐洲、中亞、東亞、拉丁美洲國家的語言多樣性,造成語言體系不一樣,不以有限字元組合的語言,尤其是中國、韓國、日本的語言最為複雜。國標2312(GB2312):《資訊交換用漢字編碼字符集-基本集》是中文編碼集,一共收錄了7445個字元,包括6763個漢字和682個其他符號。Unicode(統一碼、萬國碼、單一碼)定義了世界通用的符號集,UTF-*實現了編碼,UTF-8以位元組為單位對Unicode進行編碼。Unicode是兼容全球的字符集。
電腦的匯流排與IO設備
電腦的匯流排
什麼是匯流排?
匯流排提供了對外的介面,不同設備可以通過USB(Universal Serial Bus)介面進行連接,連接的標準,促使外圍設備介面的統一。

當我們的輸入設備向電腦中輸入資訊,要求電腦給出指定輸出時,這時需要IO匯流排來進行匯流排連接。
匯流排的分類?
- 片內匯流排:晶片內部的匯流排,暫存器與暫存器之間,暫存器與控制器、運算器之間。片內匯流排是高集成度晶片內部的資訊傳輸線。
- 系統匯流排:CPU、主記憶體、IO設備、各組件之間的資訊傳輸線
- 數據匯流排:雙向傳輸各個部件的數據資訊,數據匯流排的位數(匯流排寬度)是數據匯流排的重要參數,一般與CPU位數相同(32位、64位)
- 地址匯流排:指定源數據或目的數據在記憶體中的地址,地址匯流排的位數與存儲單元有關。若地址匯流排位數=n,定址範圍:0~2n
- 控制匯流排:控制匯流排是用來發出各種控制訊號的傳輸線,控制訊號經由控制匯流排從一個組件發給另外一個組件,控制匯流排可以監視不同組件之間的狀態(就緒/未就緒)
匯流排的仲裁:為了解決匯流排使用權的衝突問題
匯流排的仲裁方法:
- 鏈式查詢:好處:電路複雜度低,仲裁方式簡單;壞處:優先順序低的設備難以獲得匯流排的使用權,對電路故障敏感。
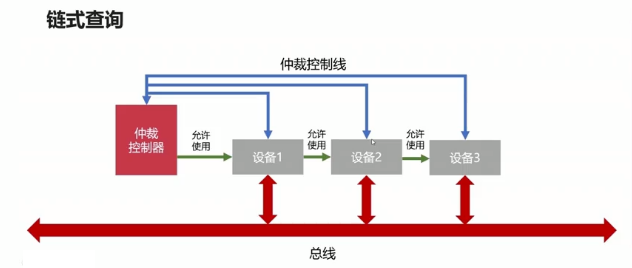
- 計時器定時查詢
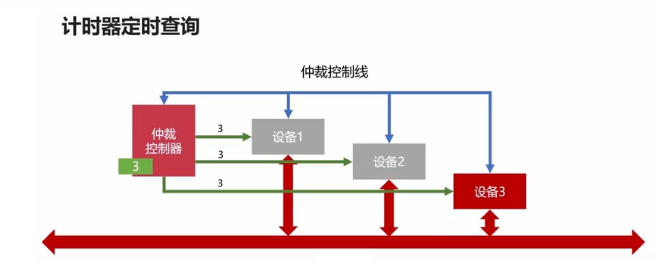
- 獨立請求
- 每個設備均有匯流排獨立連接仲裁器
- 設備可單獨向仲裁器發送請求和接受請求
- 當同時收到多個請求訊號,仲裁器有權按優先順序分配使用權
- 好處:響應速度快,優先順序可動態改變,設備連線多,匯流排控制複雜。
常見的IO設備
常見的輸入設備:分為字元輸入設備和影像輸入設備。字元輸入設備就如鍵盤,影像輸入設備如滑鼠、數位板、掃描儀等。

常見的輸出設備:顯示器、印表機、投影儀
輸入輸出介面的通用設計:我們需要考慮如何向設備發送數據?如何讀取數據?該設備有沒被佔用?設備是否已經啟動?設備是否已經連接?等等還有其他問題,基於對輸入輸出設備介面通用設計的考慮,至少應該有以下幾部分:
- 數據線
- 是I/O設備與主機之間進行數據交換的傳送線
- 單向傳輸數據線
- 雙向傳輸數據線
- 狀態線
- IO設備狀態向主機報告的訊號線
- 查詢設備是否已經正常連接並就緒
- 查詢設備是否已經被佔用
- 命令線
- CPU向設備發送命令的訊號線
- 發送讀寫訊號
- 發送啟動停止訊號
- 設備選擇線
- 主機選擇I/O設備進行操作的訊號線
- 對連在匯流排上的設備進行選擇
電腦的存儲器
存儲器的分類:
- 按存儲介質分:
- 半導體存儲器:例如記憶體、U盤、固態硬碟
- 磁存儲器:例如磁帶、磁碟等
- 按存取方式分類:
- 隨機存儲器(RAM):隨機讀取,與位置無關
- 串列存儲器:與位置有關,按順序查找
- 只讀存儲器(ROM):只讀不寫,BIOS就是存儲在只讀存儲器中
存儲器的層次:
對於存儲器,我們希望它讀寫速度快,存儲容量大,而價格最好低一些。存儲器的層次結構如下圖:

快取:指的就是CPU中的暫存器以及高速快取;主存:電腦中的記憶體;輔存:電腦的外部存儲設備,比如磁碟、U盤、移動硬碟等。

快取-主存層次:
- 原理:局部性原理,局部性原理就是指CPU訪問存儲器時,無論是存取指令還是存取數據,所訪問的存儲單元都趨集於在一個較小的連續區域中。
- 實現:在CPU與主存之間增加一層速度快(容量小)的Cache
- 目的:解決主存速度不足的問題
主存-輔存層次:
- 原理:局部性原理
- 實現:主存之外增加輔助存儲器(磁碟,SD卡,U盤等)
- 目的:解決主存容量不足的問題
電腦突然斷電,記憶體數據就會丟失,但是電腦斷電,磁碟數據不會丟失。
- 主存儲器——記憶體
- RAM(隨機存取存儲器 :Random Access Memory)
- RAM通過電容存儲數據,必須隔一段時間刷新一次
- 如果斷電,那麼一段時間後將丟失所有數據
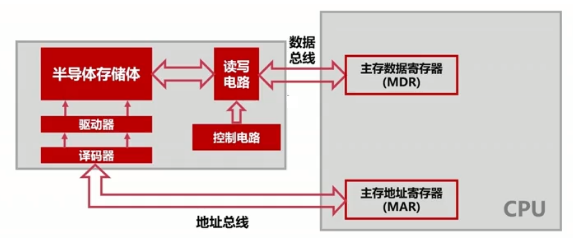
對於32位系統,電腦記憶體最大為 232 = 430 = 4GB,對於64為系統,電腦記憶體最大為 264 = 234 x 230 = 234GB
- 輔助存儲器——磁碟
- 表面是可磁化的硬磁特性材料
- 移動磁頭徑向運動讀取磁軌資訊
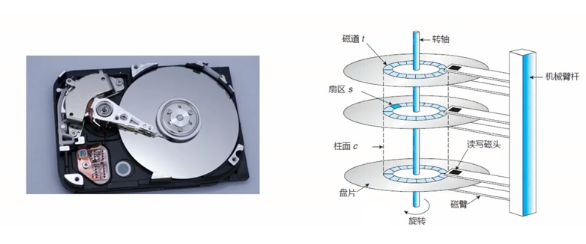
電腦的輔助存儲器常用演算法
- 先來先服務演算法
- 最短尋道時間優先
- 與磁頭當前位置有關
- 優先訪問離磁頭最近的磁軌
- 掃描演算法(電梯演算法)
- 循環掃描演算法
電腦的高速快取
高速快取的工作原理
字:是指存放在一個存儲單元中的二進位程式碼組合
字塊:存儲在連續的存儲單元中而被看作是一個單元的一組位元組
一個字快有32位,一個字快共B個字,主存中共M個字塊,則主存總字數=B*M,主存總容量(bits)=B*M*32。字的地址包含兩部分:前m位指定字快的地址,後b位指定字在字快中的地址。

例子:假設主存用戶空間容量位4G,字快大小為4M,字長為32位,則對於字地址中的快地址m和塊內地址b的位數,至少應該是多少?
由於1G=1024M,所以4G=4096M,由於字快大小為4M,所以字快數為:\(4096\div4=1024\),所以字快地址m=\(\log_2 1024=10\),塊內字數為\(4M\div32bit=1048576bit\),塊內地址b=\(\log_2 1048576=20\),所以快地址m的位數至少為10,塊內地址b的位數最少為20。
我們已經知道在CPU與主存之間存在高速快取,當CPU需要的數據在快取里時,則CPU直接從高度快取中讀取數據即可,不需要去訪問主存,但當CPU需要的數據不在快取里時,則需要去主存拿。由於CPU的處理速度遠遠快於主存的讀取速度和數據傳輸速度,所以這樣會導致CPU空轉來等待數據傳輸,造成資源上的浪費。所以我們儘可能的讓CPU去高速快取中讀取數據,因此我們需要一個量化指標,這個量化指標就是命中率。命中率是衡量快取的重要性能指標,理論上CPU每次都能從高速快取中讀取數據的時候,命中率為1。假設訪問主存次數為\(N_m\),訪問Cache次數為:\(N_c\),則命中率h為:\(h=\frac{N_c}{N_c+N_m}\)。現在來看看訪問效率e,假設訪問主存時間為\(t_m\),訪問快取時間為\(t_c\),則訪問Cache-主存系統的平均時間為:\(t_a=ht_c+(1-h)t_m\),則訪問效率e為:\(e=\frac{t_c}{t_a}=\frac{t_c}{ht_c+(1-h)t_m}\)
例子:假設CPU在執行某段程式時,共訪問了Cache命中2000次,訪問主存50次,已知Cache的存取時間為50ns,主存的存取時間為200ns,求Cache-主存系統中的命中率、訪問效率和平均訪問時間。
命中率:\(h=\frac{N_c}{N_c+N_m}=\frac{2000}{2000+50}=0.97\)
訪問效率:\(e=\frac{t_c}{t_a}=\frac{t_c}{ht_c+(1-h)t_m}=\frac{50}{0.97\ast50+(1-0.97)200}=0.917=91.7\%\)
平均訪問時間:\(0.97\ast50+(1-0.97)200=54.5ns\)
高速快取的替換策略
由於高速快取的運行需要良好的快取替換策略。什麼是快取替換策略呢?就是當高速快取中沒有數據時,需要從主存中載入所需要的數據。高速快取中常見的替換策略:
- 隨機演算法
- 先進先出演算法(FIFO)
- 最不經常使用演算法(LFU)
- 優先淘汰最不經常使用的字快
- 需要額外的空間記錄字快的使用頻率
- 最近最少使用演算法(LRU)
- 優先淘汰一段時間內沒有使用的字快
- 有多種實現方法,一般使用雙向鏈表
- 把當前訪問節點置於鏈表前面(保證鏈表頭部節點是經常使用的)
電腦的指令系統
- 機器指令的形式
機器指令主要有兩部分組成:操作碼、地址碼。地址碼直接給出操作數和操作數的地址,分三地址指令、二地址指令和一地址指令,最後還有零地址指令,零地址指令在機器指令中沒有地址碼,用來進行空操作、停機操作、中斷返回操作等。

- 機器指令的操作類型:
- 數據傳輸:在暫存器之間、暫存器與存儲單元、存儲單元之間傳送;還可以進行數據獨寫、交換地址數據、清零置一等操作。
- 算術邏輯操作:操作數之間的加減乘除運算;操作數的與或非等邏輯運算
- 移位操作:數據左移(乘2)、數據右移(除2);完成數據在算術邏輯單元的必要操作。
- 控制指令:主要有等待指令、停機指令、空操作指令、中斷指令等。
- 機器指令的定址方式
- 指令定址:順序定址;跳躍定址
- 數據定址:
- 立即定址:指令直接獲得操作數,無需訪問存儲器
- 直接定址:直接給出操作數在主存中的地址,尋找操作數簡單,無需計算數據地址
- 間接定址:指令地址碼給出的是操作數地址的地址,需要訪問一次或多次主存來獲取操作數
| 定址方式 | 優點 | 缺點 |
|---|---|---|
| 立即定址 | 速度塊 | 地址碼位數限制操作數表示範圍 |
| 直接定址 | 尋找操作數簡單 | 地址碼位數限制操作數表示範圍 |
| 間接定址 | 操作數定址範圍大 | 速度較慢 |
電腦的控制器
控制器是協調和控制電腦運行的,電腦的控制器主要組成部分如下:
- 程式計數器:程式計數器用來存儲下一條指令的地址;循環從程式計數器中拿出指令;當指令被拿出時,指向下一條指令
- 時序發生器:電氣工程領域,用於發送時序脈衝;CPU根據不同的時序脈衝有節奏的進行工作
- 指令解碼器:指令解碼器是控制器主要部件之一,電腦指令由操作碼和地址碼組成,翻譯操作碼對應的操作以及控制傳輸地址碼對應的數據
- 各種暫存器
- 指令暫存器:指令暫存器也是控制器的主要部件之一,從主存或高速快取讀取電腦指令
- 主存地址暫存器:保存當前CPU正要訪問的記憶體單元的地址
- 主存數據暫存器:保存當前CPU正要讀或寫的記憶體數據
- 通用暫存器:用於暫時存放或傳送數據和指令,可保存ALU的運算中間結果,容量比一般的專用暫存器要大
- 匯流排
電腦的運算器
運算器是用來進行數據加工運算的,主要組成部分如下:
- 數據緩衝器:分為輸入緩衝和輸出緩衝,輸入緩衝暫時存放外設送過來的數據;輸出緩衝暫時存放送往外設的數據
- ALU:算術邏輯單元,是運算器的主要組成,常見的位運算(左右移、與或非等),算數運算(加減乘除等)
- 通用暫存器
- 狀態字暫存器:存放運算狀態(條件碼、進位、溢出、結果正負等);存放運算控制資訊(調試跟蹤標記位、允許中斷位等)
- 匯流排
計算篇
進位概述
進位是一種計數方式,亦稱為進位計數法或位值計數法,用有限種數字元號來表示無線的數值,使用的數字元號的數目稱為這種進位制的基數或底數。例如n=10[0-9]稱為十進位;還有例如瑪雅文明的瑪雅數字,因努伊特的因努伊特數字使用的就是二十進位;像時間、坐標、角度等量化數據使用的就是六十進位。但我們使用的電腦喜歡二進位,但是使用二進位表達太長了,使用大進位可以解決這個問題,電腦常用的大進位有八進位、十六進位。因為八進位和十六進位都滿足2的n次方要求。例如1024分別使用二進位、八進位、十六進位表示為:1024 = 0b1000000000 = oO2000 = ox400
二進位的運算基礎
1.整數十進位和二進位的互相轉換
(整數)十進位轉換二進位:重複相除法。例子:十進位數101轉為二進位:如下
| 重複除以2 | 得商 | 取餘數 |
|---|---|---|
| 101/2 | 50 | 1 |
| 50/2 | 25 | 0 |
| 25/2 | 12 | 1 |
| 12/2 | 6 | 0 |
| 6/2 | 3 | 0 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1 |
最後,倒著取餘數,所以101的二進位表示是:1100101。二進位轉為十進位使用的是按權展開法:\(1100101 = 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 +0 \times 2^1 + 1 \times 2^0 = 101\)
再舉一個例子:十進位數237轉為二進位,如下
| 重複除以2 | 得商 | 取餘數 |
|---|---|---|
| 237/2 | 118 | 1 |
| 118/2 | 59 | 0 |
| 59/2 | 29 | 1 |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1 |
最後倒著取數,所以237的二進位表示是:11101101。使用按權展開法把二進位轉為十進位:\(11101101 = 1 \times 2^7 + 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 +0 \times 2^1 + 1 \times 2^0 = 237\)
二進位轉為十進位:按權展開法的的計算公式如下:
\(N = d_{n-1}d_{n-2}…d_1d_0 = d_{n-1}r^{n-1} + d_{n-2}r^{n-2} + d_1r +d_0\)
2.小數十進位和二進位的互相轉換
如果這個十進位是小數,則使用重複相乘法。例如 \(\frac{25}{32}\)轉為二進位,如下:
| 重複乘以2 | 得積 | 取整 |
|---|---|---|
| \(\frac{25}{32} \times 2\) | \(\frac{25}{16} = 1+\frac{9}{16}\) | 1 |
| \(\frac{9}{16} \times 2\) | \(\frac{9}{8} = 1+\frac{1}{8}\) | 1 |
| \(\frac{1}{8} \times 2\) | \(\frac{1}{4} = 0+\frac{1}{4}\) | 0 |
| \(\frac{1}{4} \times 2\) | \(\frac{1}{2} = 0+\frac{1}{2}\) | 0 |
| \(\frac{1}{2} \times 2\) | \(1 = 1+0\) | 1 |
最後順著取整數:\(\frac{25}{32}\)的二進位表示為:0.11001。現在再使用按權展開法把二進位轉為十進位數:
\(N = 0.11001 = 1 \times 2^{-1} + 1 \times 2^{-2} + 0 \times 2^{-3} + 0 \times 2^{-4} + 1 \times 2^{-5} = 0.78125 = \frac{25}{32}\)
有符號數和無符號數
正的237使用二進位表示為:+237 = 011101101 ,負的237使用二進位表示為:-237 = 111101101,在電腦中,使用0表示正數,使用1表示負數。但電腦是怎麼判斷它是數字位還是符號位的呢?這就需要使用原碼錶示法了,在原碼錶示法中,使用0表示正數,使用1表示負數,規定符號位位於數值的第一位,表達簡單明了,是我們最容易理解的表示法。0有兩種表示法:00或10,在使用原碼進行運算時,會非常複雜,特別是兩個操作符號不同的時候,我們需要進行判斷兩個操作數得絕對值大小,使用絕對值大的數減去絕對值小的數,對於符號值,以絕對值大的為準。因此我們希望找不到不同符號操作數運算更加簡單得方法,也就是可以使用正數來代替負數,使用加法操作來代替減法操作,從而消除減法。於是出現了二進位的補碼錶示法,補碼的定義如下:
\begin{cases}
x & 2^{n} > x \geq 0 \\
2^{n+1} + x & 0 > x \geq -2^n
\end{cases}
\]
例1:x=-13,計算x的二進位原碼和補碼
原碼:x=1,1101
補碼:\(2^{n+1} + x = 2^{4+1} – 13 = 100000 – 1101 = 10011\),這裡的最高位1是符號位
補碼:x = 1,0011
例2:x=-7,計算x的二進位原碼和補碼
原碼:x=1,0111
補碼:\(2^{n+1} + x = 2^{4+1} – 7 = 100000 – 0111 = 1 1001\),這裡的最高位1是符號位
補碼:x = 1,1001
例3:x=-1,計算x的二進位原碼和補碼
原碼:x=1,0001
補碼:\(2^{n+1} + x = 2^{4+1} – 1 = 100000 – 0001 = 1 1111\),這裡的最高位1是符號位
補碼:x = 1,1111
我們引入補碼的初衷是由於減法運算複雜,希望找到使用正數代替負數的方法,使用加法代替減法操作,從而消除減法,但是通過上面例子可以看到,補碼的引入,並沒有實現校除減法的目的。於是就提出了反碼,反碼的目的是找出原碼和補碼之間的規律,消除轉換過程中的減法,反碼的定義如下:
\begin{cases}
x & 2^{n} > x \geq 0 \\
(2^{n+1} – 1) + x & 0 > x \geq -2^n
\end{cases}
\]
例1:x=-13,計算x的二進位原碼和反碼
原碼:x=1,1101
補碼:\((2^{n+1} – 1) + x = (2^{4+1} -1) – 13 = 011111 – 1101 = 10010\),這裡的最高位1是符號位
補碼:x = 1,0010
例2:x=-7,計算x的二進位原碼和反碼
原碼:x=1,0111
補碼:\((2^{n+1} – 1) + x = (2^{4+1} -1) – 7 = 011111 – 0111 = 11000\),這裡的最高位1是符號位
補碼:x = 1,1000
我們可以根據反碼補碼的定義進行計算,找一找三者的關係:
| 十進位 | 原碼 | 補碼 | 反碼 |
|---|---|---|---|
| 13 | 0,1101 | 0,1101 | 0,1101 |
| -13 | 1,1101 | 1,0011 | 1,0010 |
| -7 | 1,0111 | 1,1001 | 1,1000 |
| -1 | 1,0001 | 1,1111 | 1,1110 |
根據這個表格中數據,我們可以發現正數原碼、補碼、反碼的值都是一樣的;負數的反碼等於原碼除符號位外都按位取反,負數的補碼等於反碼+1。同樣的,小數的二進位也滿足這個規律,二進位小數的補碼定義如下:
\begin{cases}
x & 1 > x \geq 0 \\
2 + x & 0 > x \geq -1
\end{cases}
\]
例1:\(x=\frac{9}{16}\),計算x的二進位原碼、反碼和補碼
原碼:x=0,0.1001 反碼:x=0,0.1001 補碼:x=0,0.1001
例2:\(x=-\frac{11}{32}\),計算x的二進位原碼、反碼和補碼
原碼:x=1,0.01011 反碼:x=1,1.10100 補碼:x=1,1.10101
定點數與浮點數
定點數的表示方法:純小數的小數點放在符號位與數值位之間,純整數的小數點放在數值位末尾,我們的定點數的保存需要乘以比例因子。
定點數的純小數表示:
| 數值 | 符號位 | 數值位 |
|---|---|---|
| 0.1011 | 0 | 1011 |
| -0.1011 | 1 | 1011 |
定點數的純整數表示:
| 數值 | 符號位 | 數值位 |
|---|---|---|
| 1011 | 0 | 1011 |
| -1011 | 1 | 1011 |
由於電腦處理的很大程度上不是純小數或純整數,如果數據範圍很大,定點數就難以表達。
浮點數的表示格式:使用科學計數法表示浮點數,\(123450000000 = 1.2345 \times 10^11\),1.2345是尾數,10是基數,11是階碼。浮點數的表示格式為:\(N = S \times r^j\),S代表尾數,r代表基數,j表示階碼,尾數規定使用純小數。例子如下:
\(N = S \times r^j\)
\(11.0101 = 0.110101 \times 2^10\),這裡都是二進位表示,階碼10對應十進位數為2
\(11.0101 = 0.0110101 \times 2^11\),這裡都是二進位表示,階碼11對應十進位數為3
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位(8位) |
|---|---|---|---|
| 0 | 10 | 0 | 11010100 |
| 0 | 11 | 0 | 01101010 |
浮點數的表示範圍:假設階碼值取m位,尾數值取n位,\(N = S \times r^j\),階碼能夠表示的最大值為:\(2^m-1\),階碼錶示範圍為:\([-(2^m-1),2^m-1]\);尾數能夠表示的最大值為:\(1 – 2^{-n}\),尾數能夠表示的最小值為:\(2^{-n}\),尾數表示的範圍為:\([-(1 – 2^{-n}),-2^{-n}]\) \([2^{-n},1-2^{-n}]\)

單精度浮點數:使用4位元組、32位來表示浮點數(float)
雙精度浮點數:使用8位元組、64位來表示浮點數(double)
浮點數的規格化:尾數規定使用純小數,尾數最高位必須是1.
例1:設浮點數的長度為16位,階碼為5位,尾數為是11位,將十進位數\(\frac{13}{128}\)表示為二進位浮點數
由於正數的原碼=反碼=補碼:\(x = 0.0001101000\),浮點數的規格化:\(x = 0.1101000 * 2^{-11}\)
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 1 | 0011 | 0 | 1101000000 |
例2:設浮點數的長度為16位,階碼為5位,尾數為是11位,將十進位數\(-54\)表示為二進位浮點數
原碼:\(x = 1,110110\),浮點數的規格化:\(x = -0.110110 * 2^{-110}\),由於尾數為110110 0000,則尾數反碼為:001001 1111,尾數補碼為:001010 0000
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 0 | 0110 | 1 | 001010 0000 |
定點數與浮點數的對比:
- 定點數與浮點數位數相同時,浮點數表示的範圍更大
- 當浮點數尾數為規格化數時,浮點數的精度更高
- 浮點數運算包含階碼和位數,浮點數的運算更為複雜
總結:浮點數在數的表示範圍、精度、溢出處理、編程等方面均優於定點數;浮點數在數的運算規則、運算速度、硬體成本等方面不如定點數。
定點數的加減法運算
整數加法:A[補] + B[補] = [A+B][補](mod\(2^{n+1}\))
小數加法:A[補] + B[補] = [A+B][補](mod2)
注意:定點數的加減法運算,數值位與符號位一同運算,並將符號位產生的進位自然丟掉
例1:A=-110010,B=001101,求A+B
A[補] = 1,001110,B[補] = B[原] = 0,001101,A[補] + B[補] = (A+B)[補] = 1,011011,則A + B = -100101
例2:A=-0.1010010,B=0.0110100,求A+B
A[補] = 1,1.0101110,B[補] = B[原] = 0.0110100,A[補] + B[補] = (A+B)[補] = 1,1.1100010,則A + B = -0.0011110
例3:A=-10010000,B=-11010000,求A+B
A[補] = 1,01110000,B[補] = 1,00110000,A[補] + B[補] = (A+B)[補] = 0,10100000,則A + B = 10100000,將結果轉為十進位表示是160。我們可以把A和B轉為十進位進行運算:A=-144,B=-208,A+B=-352,我們會發現二進位的計算結果是錯誤的。這是由於我們在計算時,對符號位的進位自然丟掉了,這是就發生了溢出,那我們如何來判斷溢出呢?雙符號位判斷法:單符號位表示變成雙符號位:0=>00,1=>11,雙符號位產生的進位丟棄,結果的雙符號位不同則表示溢出。
整數減法:A[補] – B[補] = A + (-B)[補](mod\(2^{n+1}\))
小數減法:A[補] – B[補] = A + (-B)[補](mod2)
-B[補]等於B[補]連同符號位按位取反,末位加一
浮點數的加減法運算
運算過程:對階->尾數求和->尾數規格化->舍入->溢出判斷
\(x = 0.1101 \times 2^{01}\)
\(y = (-0.1010) \times s^{11}\)
對階:浮點數尾數運算簡單,浮點數位數實際小數位與階碼有關,階碼按小階看齊大階的原則。對階的目的是使得兩個浮點數階碼一致,使得尾數可以進行運算
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 00 | 0001 | 00 | 1101 |
| 00 | 0011 | 11 | 1010 |
對階後:
\(x = 0.001101 \times 2^{11}\)
\(y = (-0.1010) \times s^{11}\)
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 00 | 0011 | 00 | 0011(01) |
| 00 | 0011 | 11 | 1010 |
捨去01,在進行尾數求和,x[原]=00.0011,x[補]=00.0011,y[原]=11.1010,y[補]=11.0110,S=(x+y)[補]=11.1001
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 00 | 0011 | 11 | 1001 |
尾數規格化:對補碼進行規格化需要判斷兩種情況:S>0和S<0,S[補] = 00.1xxxxxxx(S>0),S[補] = 11.0xxxxxxx(S<0),符號位與最高位不一致,如果不滿足此格式,則需要進行左移,同時階碼相應變化,以滿足規格變化。
| 階碼符號位 | 階碼數值位 | 尾數符號位 | 尾數數值位 |
|---|---|---|---|
| 00 | 0011 | 11 | 1001 |
S = (x + y)[補] = 11.1001 = 11.(1)0010







