你對YOLOV3損失函數真的理解正確了嗎?
1. 前言
昨天行雲大佬找到我提出了他關於 GiantPandaCV 公眾號出版的《從零開始學 YOLOV3》電子書中關於原版本的 YOLOV3 損失的一個質疑,並給出了他的理解。昨天晚上我仔細又看了下原始論文和 DarkNet 源碼,發現在 YOLOV3 的原版損失函數的解釋上我誤導了不少人。所以就有了今天這篇文章,與其說是文章不如說是一個錯誤修正吧。
2. 在公眾號裡面的 YOLOV3 損失函數
在我們公眾號出版的 YOLOV3 的 PDF 教程里對原始的 DarkNet 的損失函數是這樣解釋的,這個公式也是我參照源碼(//github.com/BBuf/Darknet/blob/master/src/yolo_layer.c)進行總結的,。 我的總結截圖如下:

其中S表示grid\ size,S^2表示13\times 13,26\times 26, 52\times 52。B 代表 box,1_{ij}^{obj}表示如果在i,j處的 box 有目標,其值為1,否則為0。1_{ij}^{noobj}表示如果i,j處的 box 沒有目標,其值為1,否則為0。
BCE(binary cross entropy)的具體公式計算如下:
BCE(\hat(c_i),c_i)=-\hat{c_i}\times log(c_i)-(1-\hat{c_i})\times log(1-c_i)
另外,針對 YOLOV3,回歸損失會乘以一個2-w*h的比例係數,w和h代表Ground Truth box的寬高,如果沒有這個係數 AP 會下降明顯,大概是因為 COCO 數據集小目標很多的原因。
我根據 DarkNet 的源碼對每一步進行了梯度推導發現損失函數的梯度是和上面的公式完全吻合的,所以當時以為這是對的,感謝行雲大佬提醒讓我發現了一個致命理解錯誤,接下來我們就說一下。
3. 行雲大佬的損失函數公式
接下來我們看一下行雲大佬的損失函數公式,形式如下:
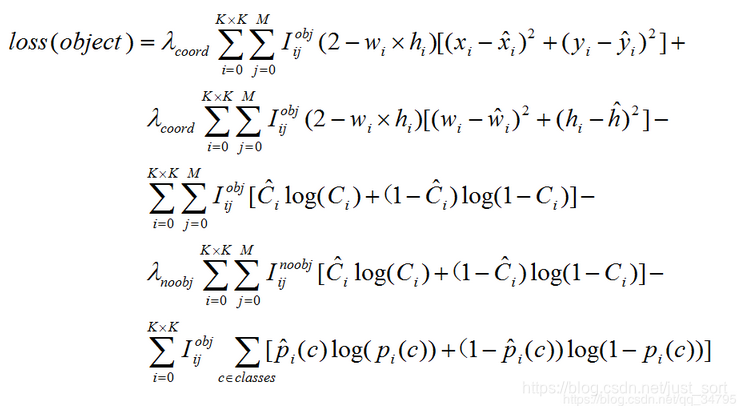
可以看到我的損失函數理解和行雲大佬的損失函數理解在回歸損失以及分類損失上是完全一致的,只有 obj loss 表示形式完全不同。對於 obj loss,我的公式裡面是方差損失,而行雲大佬是交叉熵損失。那麼這兩種形式哪一種是正確的呢?
其實只要對交叉熵損失和方差損失求個導問題就迎刃而解了。
4. 交叉熵損失求導數
推導過程如下:
(1)softmax 函數
首先再來明確一下 softmax 函數,一般 softmax 函數是用來做分類任務的輸出層。softmax 的形式為:
S_i = \frac{e^{z_i}}{\sum_ke^{z_k}}
其中S_i表示的是第 i 個神經元的輸出,接下來我們定義一個有多個輸入,一個輸出的神經元。神經元的輸出為
z_i = \sum_{ij}x_{ij}+b
其中w_{ij}是第i個神經元的第j個權重,b 是偏移值.z_i表示網路的第i個輸出。給這個輸出加上一個 softmax 函數,可以寫成:
a_i = \frac{e^{z_i}}{\sum_ke^{z_k}},
其中a_i表示 softmax 函數的第i個輸出值。這個過程可以用下圖表示:
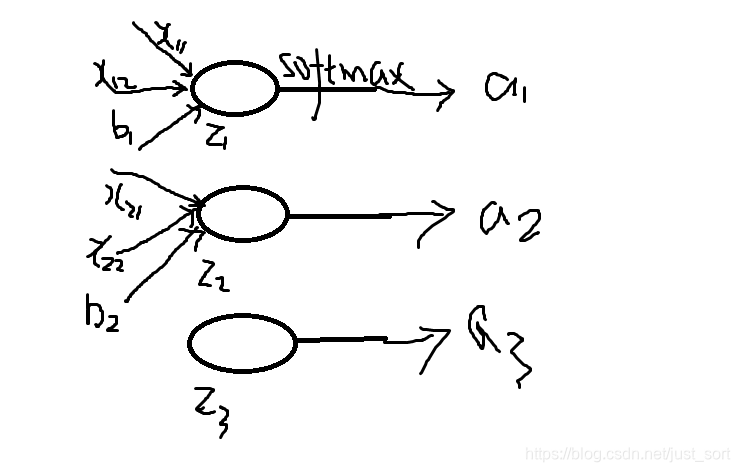
(2)損失函數
softmax 的損失函數一般是選擇交叉熵損失函數,交叉熵函數形式為:
C=-\sum_i{y_i lna_i}
其中 y_i 表示真實的標籤值
(3)需要用到的高數的求導公式
c'=0(c為常數)
(x^a)'=ax^(a-1),a為常數且a≠0
(a^x)'=a^xlna
(e^x)'=e^x
(logax)'=1/(xlna),a>0且 a≠1
(lnx)'=1/x
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=(secx)^2
(secx)'=secxtanx
(cotx)'=-(cscx)^2
(cscx)'=-csxcotx
(arcsinx)'=1/√(1-x^2)
(arccosx)'=-1/√(1-x^2)
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
(shx)'=chx
(chx)'=shx
(uv)'=uv'+u'v
(u+v)'=u'+v'
(u/)'=(u'v-uv')/^2
(4)進行推導
我們需要求的是 loss 對於神經元輸出z_i的梯度,求出梯度後才可以反向傳播,即是求:
\frac{\partial C}{\partial z_i}, 根據鏈式法則(也就是複合函數求導法則)\frac{\partial C}{\partial a_j}\frac{\partial a_j}{\partial z_i},初學的時候這個公式理解了很久,為什麼這裡是a_j而不是a_i呢?這裡我們回憶一下 softmax 的公示,分母部分包含了所有神經元的輸出,所以對於所有輸出非 i 的輸出中也包含了z_i,所以所有的 a 都要參與計算,之後我們會看到計算需要分為i=j和i \neq j兩種情況分別求導數。
首先來求前半部分:
\frac{\partial C}{ \partial a_j} = \frac{-\sum_jy_ilna_j}{\partial a_j} = -\sum_jy_j\frac{1}{a_j}
接下來求第二部分的導數:
- 如果i=j,\frac{\partial a_i}{\partial z_i} = \frac{\partial(\frac{e^{z_i}}{\sum_ke^{z_k}})}{\partial z_i}=\frac{\sum_ke^{z_k}e^{z_i}-(e^{z_i})^2}{(\sum_ke^{z_k})^2}=(\frac{e^z_i}{\sum_ke^{z_k}})(1 – \frac{e^{z_i}}{\sum_ke^{z_k}})=a_i(1-a_i)
- 如果i \neq j,\frac{\partial a_i}{\partial z_i}=\frac{\partial\frac{e^{z_j}}{\sum_ke^{z_k}}}{\partial z_i} = -e^{z_j}(\frac{1}{\sum_ke^z_k})^2e^{z_i}=-a_ia_j。
接下來把上面的組合之後得到:
\frac{\partial C}{\partial z_i}
=(-\sum_{j}y_j\frac{1}{a_j})\frac{\partial a_j}{\partial z_i}
=-\frac{y_i}{a_i}a_i(1-a_i)+\sum_{j \neq i}\frac{y_j}{a_j}a_ia_j
=-y_i+y_ia_i+\sum_{j \neq i}\frac{y_j}a_i
=-y_i+a_i\sum_{j}y_j。
推導完成!
(5)對於分類問題來說,我們給定的結果y_i最終只有一個類別是 1,其他是 0,因此對於分類問題,梯度等於:
\frac{\partial C}{\partial z_i}=a_i – y_i
5. L2 損失求導數
推導如下:
我們寫出 L2 損失函數的公式:
L2_{loss}=(y_i-a_i)^2,其中y_i仍然代表標籤值,a_i表示預測值,同樣我們對輸入神經元(這裡就是a_i了,因為它沒有經過任何其它的函數),那麼\frac{\partial C}{\partial z_i}=2(a_i – y_i),其中z_i=a_i。
注意到,梯度的變化由於有學習率的存在所以係數是無關緊要的(只用關心數值梯度),所以我們可以將係數省略,也即是:
\frac{\partial C}{\partial z_i}=a_i – y_i
6. 在原論文求證
可以看到無論是 L2 損失還是交叉熵損失,我們獲得的求導形式都完全一致,都是output-label的形式,換句話說兩者的數值梯度趨勢是一致的。接下來,我們去原論文求證一下:


上面標紅的部分向我們展示了損失函數的細節,我們可以發現原本 YOLOV3 的損失函數在 obj loss 部分應該用二元交叉熵損失的,但是作者在程式碼里直接用方差損失代替了。
至此,可以發現我之前的損失函數解釋是有歧義的,作者的本意應該是行雲大佬的損失函數理解那個公式(即 obj loss 應該用交叉熵,而不是方法差損失),不過恰好訓練的時候損失函數是我寫出的公式(obj loss 用方差損失)。。。神奇吧。
7. 總結
本文根據行雲大佬的建議,通過手推梯度並在原始論文找證據的方式為大家展示了 YOLOV3 的損失函數的深入理解,如果有任何疑問可以在留言區留言交流。
8. 參考
- YOLOV3 論文://pjreddie.com/media/files/papers/YOLOv3.pdf
- DarkNet 原始程式碼://github.com/BBuf/Darknet/blob/master/src/yolo_layer.c
- 行雲大佬部落格://blog.csdn.net/qq_34795071/article/details/92803741
歡迎關注 GiantPandaCV, 在這裡你將看到獨家的深度學習分享,堅持原創,每天分享我們學習到的新鮮知識。( • ̀ ω•́ )✧
有對文章相關的問題,或者想要加入交流群,歡迎添加 BBuf 微信:

為了方便讀者獲取資料以及我們公眾號的作者發布一些 GitHub 工程的更新,我們成立了一個 QQ 群,二維碼如下,感興趣可以加入。



