深度學習中的一些組件及使用技巧

2020 年 5 月 18 日
筆記
技術

【說在前面】本人部落格新手一枚，象牙塔的老白，職業場的小白。以下內容僅為個人見解，歡迎批評指正，不喜勿噴！[認真看圖][認真看圖]

【補充說明】深度學習有多火，我就不多說了。本文主要介紹深度學習項目實踐過程中可能遇到的一些組件及使用技巧！

一、Optimizor優化器選擇

1. 梯度下降：經典

梯度下降的通用計算公式如下：

$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1})}$
$\Delta{\theta_t}=-\eta*g_t$

其中， $\eta$ 是學習率， $g_t$ 是梯度。梯度下降完全依賴於當前的梯度，所以 $\eta$ 可理解為允許當前梯度多大程度影響參數更新。

梯度下降主要包含三種梯度下降：

（1）批量梯度下降（Batch Gradient Descent）

使用所有的訓練樣本來更新每次迭代中的模型參數

（2）隨機梯度下降（Stochastic Gradient Descent）

在每次迭代中，僅使用單個訓練樣本更新參數（訓練樣本通常是隨機選擇的）

（3）小批量梯度下降（Mini-Batch Gradient Descent）：這個最常用

訓練時不是使用所有的樣本，而是取一個批次的樣本來更新模型參數
小批量梯度下降試圖在隨機梯度下降的穩健性和批量梯度下降的效率之間找到平衡

梯度下降的缺點：

選擇合適的learning rate比較困難
對所有的參數更新均使用同樣的learning rate
可能被困在鞍點，容易產生局部最優，不能達到全局最優

2. Momentum

Momentum是模擬物理里動量的概念，公式如下：

$m_t=\mu*m_{t-1}+g_t$
$\Delta{\theta_t}=-\eta*m_t$

其中， $\mu$ 是動量因子。Momentum積累之前的動量來替代真正的梯度。

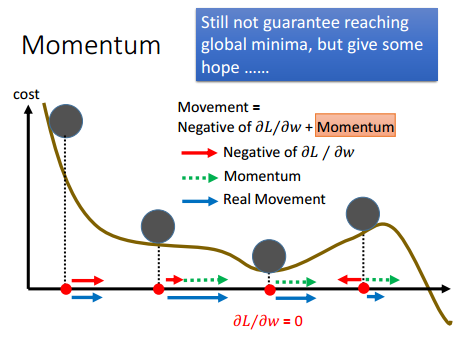
Momentum有如下特點：

下降初期時，由於下降方向和梯度方向一致，而使t時刻的動量和變化量變大，從而達到加速的目的
下降中後期時，在局部最小值來回震蕩的時候，使得更新幅度增大，跳出陷阱
在梯度改變方向的時候，能夠減少更新

總的來說，Momentum可以加速SGD演算法的收斂速度，並且降低SGD演算法收斂時的震蕩。

3. Nesterov

將上一節中的公式展開可得：

可以看出，Momentum並沒有直接改變當前梯度。Nesterov的改進就是讓之前的動量直接影響當前的動量。即：

$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1}-\eta*\mu*m_{t-1})}$
$m_t=\mu*m_{t-1}+g_t$
$\Delta{\theta_t}=-\eta*m_t$

其中，加上Nesterov項後，梯度在大的跳躍後，再計算當前梯度進行校正。

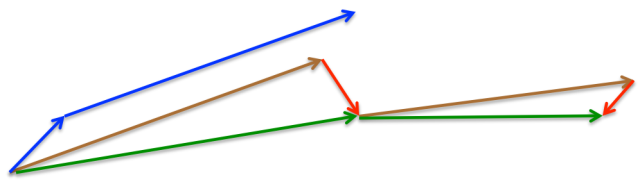
Nesterov有如下特點：

對於Momentum，首先計算一個梯度(短的藍色向量)，然後在加速更新梯度的方向進行一個大的跳躍(長的藍色向量)
對於Nesterov，首先在之前加速的梯度方向進行一個大的跳躍(棕色向量)，然後計算梯度進行校正(綠色梯向量)

總的來說，Nesterov項在梯度更新時做了一個校正，避免前進太快，同時提高靈敏度。

以上三種方法均需要人工設置一些學習率，接下來介紹幾種自適應學習率的方法！

4. Adagrad

Adagrad對學習率進行了一個約束。即：

$n_t=n_{t-1}+g_t^2$
$\Delta{\theta_t}=-\frac{\eta}{\sqrt{n_t+\epsilon}}*g_t$

其中，對 $g_t$ 從1到 $t$ 進行一個遞推，形成一個約束項regularizer， $\epsilon$ 用來保證分母非0。

Adagrad有如下特點：

前期 $g_t$ 較小的時候，regularizer較大，能夠放大梯度
後期 $g_t$ 較大的時候，regularizer較小，能夠約束梯度
高頻特徵更新步長較小，低頻特徵更新較大，適合處理稀疏梯度
能夠自適應學習率，避免了手動調整學習率的麻煩

Adagrad的缺點：

由公式可以看出，仍依賴於人工設置一個全局學習率
$\eta$ 設置過大的話，會使regularizer過於敏感，對梯度的調節太大
中後期，分母上梯度平方的累加將會越來越大，使 $gradient\to0$ ，使得訓練提前結束

5. Adadelta

Adadelta是對Adagrad的擴展，它主要解決了adagrad演算法單調遞減學習率的問題。Adagrad會累加之前所有的梯度平方，而Adadelta只累加固定大小的項，並且也不直接存儲這些項，僅僅是近似計算對應的平均值。即：

$n_t=\nu*n_{t-1}+(1-\nu)*g_t^2$
$\Delta{\theta_t} = -\frac{\eta}{\sqrt{n_t+\epsilon}}*g_t$

其中，Adadelta還是依賴於全局學習率，但是做了一定處理，經過近似牛頓迭代法之後：

$E|g^2|_t=\rho*E|g^2|_{t-1}+(1-\rho)*g_t^2$
$\Delta{x_t}=-\frac{\sqrt{\sum_{r=1}^{t-1}\Delta{x_r}}}{\sqrt{E|g^2|_t+\epsilon}}$

其中， $E$ 代表求期望。此時，可以看出Adadelta已經不用依賴於全局學習率了。

Adadelta還有如下特點：

訓練初中期，加速效果不錯，很快
訓練後期，反覆在局部最小值附近抖動

6. RMSprop

RMSprop可以算作Adadelta的一個特例，同樣是用於解決adagrad演算法學習率消失的問題。

當 $\rho=0.5$ 時， $E|g^2|_t=\rho*E|g^2|_{t-1}+(1-\rho)*g_t^2$ 就變為了求梯度平方和的平均數。

如果再求根的話，就變成了RMS(均方根)：

$RMS|g|_t=\sqrt{E|g^2|_t+\epsilon}$

此時，這個RMS就可以作為學習率 $\eta$ 的一個約束：

$\Delta{x_t}=-\frac{\eta}{RMS|g|_t}*g_t$

RMSprop有如下特點：

依然依賴於全局學習率
是Adagrad的一種發展，也是Adadelta的變體，效果趨於二者之間
適合處理非平穩目標

7. Adam：常用

Adam本質上是帶有動量項的RMSprop，它利用梯度的一階矩估計和二階矩估計動態調整每個參數的學習率。

經過偏置校正後，每一次迭代學習率都有個確定範圍，使得參數比較平穩。公式如下：

$m_t=\mu*m_{t-1}+(1-\mu)*g_t$
$n_t=\nu*n_{t-1}+(1-\nu)*g_t^2$
$\hat{m_t}=\frac{m_t}{1-\mu^t}$
$\hat{n_t}=\frac{n_t}{1-\nu^t}$
$\Delta{\theta_t}=-\frac{\hat{m_t}}{\sqrt{\hat{n_t}}+\epsilon}*\eta$

其中， $m_t$ ， $n_t$ 分別是對梯度的一階矩估計和二階矩估計，可以看作對期望 $E|g_t|$ ， $E|g_t^2|$ 的估計； $\hat{m_t}$ ， $\hat{n_t}$ 是對 $m_t$ ， $n_t$ 的校正，這樣可以近似為對期望的無偏估計。可以看出，直接對梯度的矩估計對記憶體沒有額外的要求，而且可以根據梯度進行動態調整，而 $-\frac{\hat{m_t}}{\sqrt{\hat{n_t}}+\epsilon}$ 對學習率形成一個動態約束，而且有明確的範圍。

Adam有如下特點：

結合了Adagrad善於處理稀疏梯度和RMSprop善於處理非平穩目標的優點
對記憶體需求較小
為不同的參數計算不同的自適應學習率
也適用於大多非凸優化，適用於大數據集和高維空間

8. 其他

例如Adamax（Adam的一種變體）、Nadam（類似於帶有Nesterov動量項的Adam）等，這裡不展開了。

9. 經驗總結

對於稀疏數據，使用學習率可自適應的優化方法（例如Adagrad/Adadelta/RMSprop/Adam等），且最好採用默認值
SGD通常訓練時間更長，但是在好的初始化和學習率調度方案的情況下，結果更可靠
如果需要更快的收斂，或者是訓練更深更複雜的神經網路，需要用一種自適應的演算法

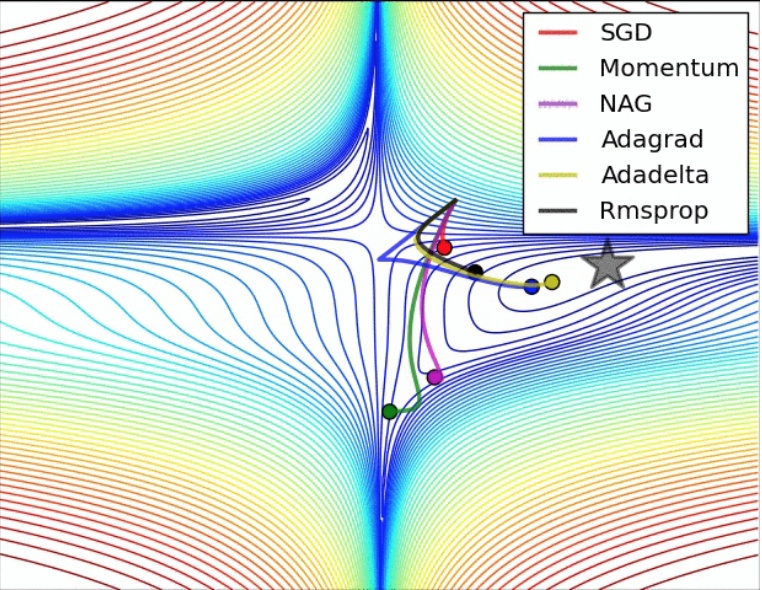
二、激活函數選擇

1. 常用的激活函數

發現這麼寫下去，篇幅太大了，所以找到一張圖，概括一下吧：

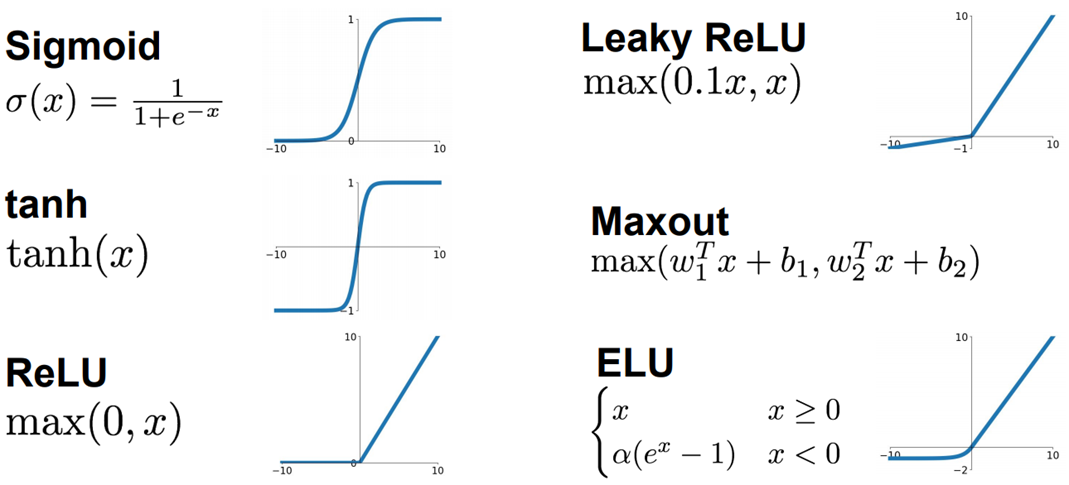
常用的主要是這些吧，各種激活函數的特點看圖也顯而易見，其他的（例如PReLU等）就不拓展了。

2. 經驗總結

對於輸出層：二分類任務一般選用Sigmoid輸出，多分類任務一般選用Softmax輸出，回歸任務一般選用線性輸出。
對於中間隱層：優先選擇Relu激活函數（Relu可以有效解決Sigmoid和tanh出現的梯度彌散問題，且能更快收斂）。

三、防止過擬合

1. 數據集擴充

即增大訓練集的規模，實在難以獲得新數據也可以使用數據集增強的方法。

例如可以對影像數據集採用水平/垂直旋轉/翻轉、隨機改變亮度和顏色、隨機模糊影像、隨機裁剪等方法進行數據集增強。

2. L1/L2正則化

正則化，就是在原來的loss function的基礎上，加上了一些正則化項或者稱為模型複雜度懲罰項。

以線性回歸為例，優化目標：

min $1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} }$

加上L1正則項（lasso回歸）：
min $1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} } + C||\omega||_{1}$

加上L2正則項（嶺回歸）：

min $1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} } + C||\omega||_{2}^{2}$

其中，L1範數更容易得到稀疏解（解向量中0比較多）；L2範數能讓解比較小（靠近0），但是比較平滑（不等於0）。

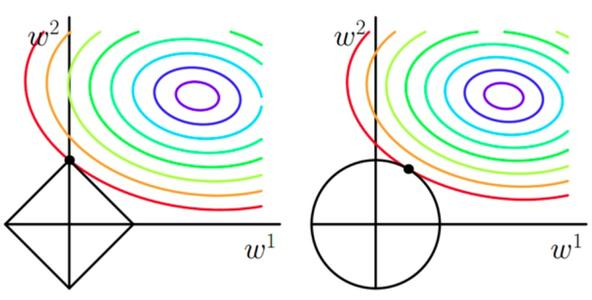
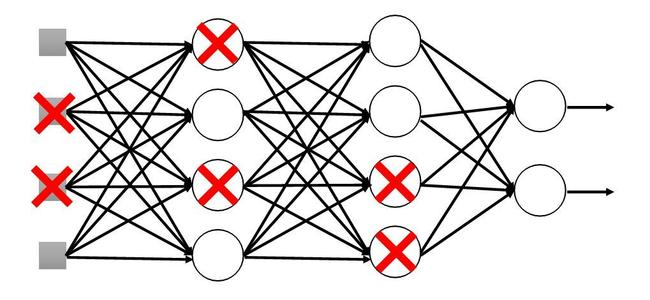
3. Dropout

Dropout提供了一個簡單的方法來提升性能。其實相當於做簡單的Ensemble，但訓練速度會慢一些。

4. 提前終止Early stopping

5. 交叉驗證

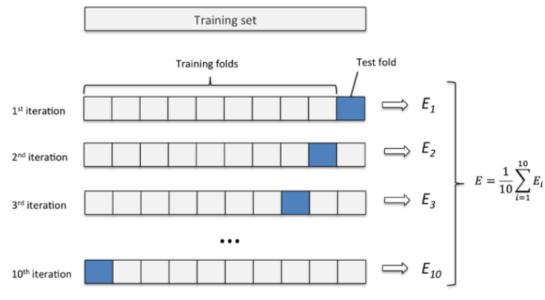
剩下就是選擇合適的模型和網路結構了，甚至可以採用多模型融合等思路。

四、防止梯度消失/爆炸

1. 使用合適的激活函數：ReLU等

解決Sigmoid函數存在的梯度消失/爆炸問題。

2. 預訓練加微調：DBN等

Hinton為了解決梯度的問題，提出採取無監督逐層訓練方法，其基本思想是每次訓練一層隱節點，訓練時將上一層隱節點的輸出作為輸入，而本層隱節點的輸出作為下一層隱節點的輸入，此過程就是逐層「預訓練」。在預訓練完成後，再對整個網路進行「微調」。

3. 梯度剪切、正則

梯度剪切這個方案主要是針對梯度爆炸提出的，其思想是設置一個梯度剪切閾值，然後更新梯度的時候，如果梯度超過這個閾值，那麼就將其強制限制在這個範圍之內。另外一種解決梯度爆炸的手段是採用權重正則化，比較常見的是L1正則和L2正則，以上已經提到了。

4. Batch Normalization

對每一層的輸出做scale和shift的方法，通過一定的規範化手段，把每層神經網路任意神經元這個輸入值的分布強行拉回到接近均值為0方差為1的標準正太分布，即嚴重偏離的分布強制拉回比較標準的分布。這樣使得激活輸入值落在非線性函數對輸入比較敏感的區域，這樣輸入的小變化就會導致損失函數較大的變化，使得讓梯度變大，避免梯度消失問題產生。而且梯度變大意味著學習收斂速度快，能大大加快訓練速度。

5. 殘差結構 `Resnet`

如果你希望訓練一個更深更複雜的網路，那麼殘差塊絕對是一個重要的組件，它可以讓你的網路訓練的更深。

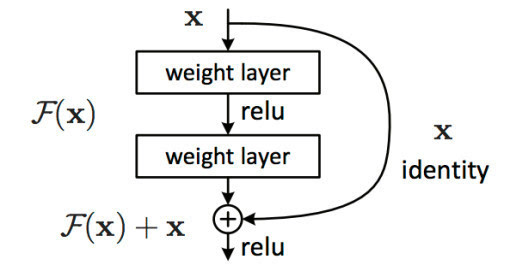
6. 採用LSTM等模型

我在序列模型專題有介紹到LSTM，這裡不再贅述。

五、權值初始化

1. 隨機初始化

有一些常用的初始化方法：

直接用0.02*randn(num_params)來初始化，當然別的值也可以。
依次初始化每一個weight矩陣，用init_scale / sqrt(layer_width) * randn，init_scale可以被設置為0.1或者1。

初始化很重要，知乎大佬們的慘痛教訓：

用normal初始化CNN的參數，最後acc只能到70%多，僅僅改成xavier，acc可以到98%。
初始化word embedding，使用了默認的initializer，速度慢且效果不好。改為uniform，訓練速度和結果也飆升。

2. 遷移學習

可以採用遷移學習預訓練的方式。說到這裡，我之後想寫一個遷移學習的專題。

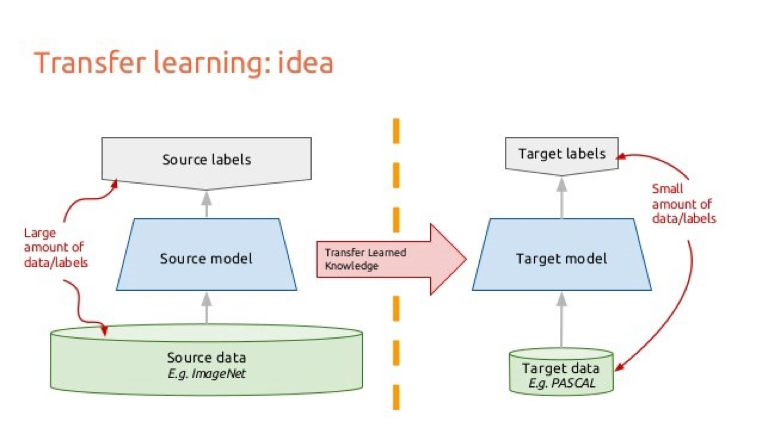
六、數據預處理

1. 標準化/歸一化處理

就是0均值和1方差化。主要是為了公平對待每個特徵、使優化過程變得平穩、消除量綱影響等。

2. Shuffle處理

在訓練的過程中，如果數據很整齊，那每次學習到的特徵都是與某一個特徵相關，會讓學習效果有所偏差。

因此，一般在訓練的過程中，建議要將數據打亂，這樣才能夠更好的實現泛化能力。

七、學習率 learning rate

一般建議從一個正常大小的學習率開始，朝著終點不斷縮小。

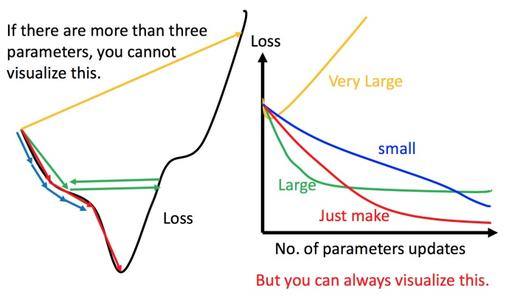
八、批次大小 batch_size

batch_size會影響優化過程，建議值取64和128等，太小訓練速度慢，太大容易過擬合。

九、損失函數 Loss

1. 多分類問題選用Softmax+交叉熵

當Sigmoid函數和MSE一起使用時會出現梯度消失。原因如下：

MSE對參數的偏導：

$在這裡插入圖片描述$
$在這裡插入圖片描述$

corss-entropy對參數的偏導：

$在這裡插入圖片描述$
$在這裡插入圖片描述$

以上，相對於Sigmoid求損失函數，在梯度計算層面上，交叉熵對參數的偏導不含對Sigmoid函數的求導，而均方誤差MSE等則含有Sigmoid函數的偏導項。同時，Sigmoid的值很小或者很大時梯度幾乎為零，這會使得梯度下降演算法無法取得有效進展，交叉熵則避免了這一問題。

為了彌補Sigmoid 型函數的導數形式易發生飽和的缺陷，可以引入Softmax作為預測結果，再計算交叉熵損失。由於交叉熵涉及到計算每個類別的概率，所以在神經網路中，交叉熵與Softmax函數緊密相關。

十、其他

例如訓練時可以先用一小部分數據集跑，看看損失的變化趨勢，有助於更快找到錯誤並調整網路結構等技巧。

另外，看到一張不同參數對於網路訓練的影響程度圖，分享一下：

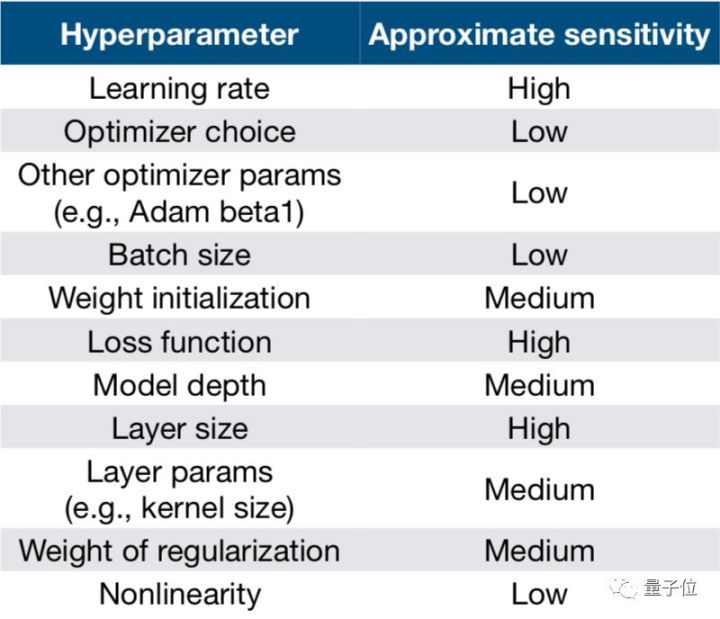
最後，雖然有很多組件和技巧可以方便使用（框架中一般都封裝好了），但是還是需要注意各組件、技巧之間的靈活組合，才能取得最佳結果。

如果您對數據挖掘感興趣，歡迎瀏覽我的另幾篇部落格：數據挖掘比賽/項目全流程介紹

如果你對智慧推薦感興趣，歡迎先瀏覽我的另幾篇隨筆：智慧推薦演算法演變及學習筆記

如果您對人工智慧演算法感興趣，歡迎瀏覽我的另一篇部落格：人工智慧新手入門學習路線和學習資源合集（含AI綜述/python/機器學習/深度學習/tensorflow）、人工智慧領域常用的開源框架和庫（含機器學習/深度學習/強化學習/知識圖譜/圖神經網路）

如果你是電腦專業的應屆畢業生，歡迎瀏覽我的另外一篇部落格：如果你是一個電腦領域的應屆生，你如何準備求職面試？

如果你是電腦專業的本科生，歡迎瀏覽我的另外一篇部落格：如果你是一個電腦領域的本科生，你可以選擇學習什麼？

如果你是電腦專業的研究生，歡迎瀏覽我的另外一篇部落格：如果你是一個電腦領域的研究生，你可以選擇學習什麼？

如果你對金融科技感興趣，歡迎瀏覽我的另一篇部落格：如果你想了解金融科技，不妨先了解金融科技有哪些可能？

之後部落客將持續分享各大演算法的學習思路和學習筆記：hello world: 我的部落格寫作思路

Tags: 技術