1018 Public Bike Management (30分) 思路分析 + 滿分程式碼
題目
There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.
The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.
When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.
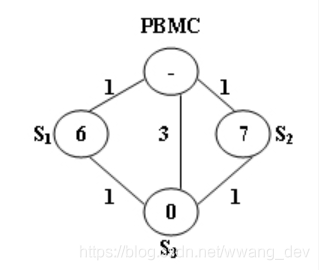
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S3 , we have 2 different shortest paths:
PBMC -> S1 -> S3 . In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S1 and then take 5 bikes to S3 , so that both stations will be in perfect conditions.PBMC -> S2 -> S3 . This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.
Input Specification:
Each input file contains one test case. For each case, the first line contains 4 numbers: Cmax (≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; Sp , the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C
i (i=1,⋯,N) where each Ci is the current number of bikes at Si respectively. Then M lines follow, each contains 3 numbers: Si , Sj , and Tij which describe the time Tij taken to move betwen stations Si and Sj . All the numbers in a line are separated by a space.
Output Specification:
For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S
1 −>⋯−>Sp . Finally after another space, output the number of bikes that we must take back to PBMC after the condition of Sp is adjusted to perfect.
Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge’s data guarantee that such a path is unique.
Sample Input:
10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1
Sample Output:
3 0->2->3 0
中文翻譯
杭州市設有公共自行車服務,為來自世界各地的遊客提供了極大的便利。可以在任何車站租用一輛自行車,然後將其還給城市中的其他車站。
公共自行車管理中心(PBMC)不斷監視所有站點的實時容量。如果工作站剛滿一半,則稱其處於理想狀態。如果一個車站已滿或空了,PBMC會收集或派送自行車以將該車站的狀況調整到最佳狀態。而且,途中的所有車站也會調整到完美狀態。
當報告問題站點時,PBMC將始終選擇到達該站點的最短路徑。如果最短路徑多於一條,則將選擇需要從PBMC發送的自行車數量最少的那條路徑。
思路分析
- 首先,遇到最短路徑,肯定是
Dijstra,但題目說了,可能會有多條最短路徑,我們要找到全部路徑怎麼辦?把每一個路徑都保存下來嗎?可以,但沒必要。我們只需要記錄最短路徑上每個節點的直接前驅就可以了,而這個,在Dijstra演算法中,只需要在更新過程中(d[v] = d[u] + e[u][v])加上一條語句就可以了(prev[v].push_back(u)),非常簡單。如果它有多個最短路徑,那麼它就有多個直接前驅,因此,每個節點都應該有一個vector來保存它的全部最短路徑的直接前驅,最終,就是需要一個vector數組。 - 找到最短路徑顯然是不夠的,我們還要進行選擇,選擇PCBC按哪一條路走,需要帶過去的自行車最少。所以,我們要遍歷全部最短路徑,於是
dfs就出場了,因為我們保存的是它的直接前驅,所以需要從sp往PCBC去遍歷。對於每一個最短路徑,模擬一次PCBC需要進行的調整過程(逐個訪問節點,並根據它的當前容量計算它達到完美需要的自行車參數),記錄需要帶過來或帶回去的自行車數目,如果更少,則選擇這條路徑。 - 有一個好的技巧是,我們的完美狀態是
cmax/2,剛開始給出了所有站點的當前容量,但我們不直接保存它的當前容量,我們用diff數組保存每個站點當前容量與完美狀態的差值,這樣,我們很容易根據這個值的正負知道它是缺少自行車,缺少幾個?或者是需要自行車,需要幾個?當然,這不是我這個菜雞能想出來的,還是參考了柳婼大神的程式碼之後改出來的,大神是真的強!!! - 所以,總的來說就是,Dijstra找到全部最短路徑,dfs遍歷每個最短路徑並找到最好的那個,選擇路徑的原則就是,
距離最短>距離相同但發送的自行車最少>距離相同發送的自行車也相同但帶回的自行車最少。 - 這裡有個問題就是,如果PCBC最終需要發送自行車,那麼帶回的自行車就是0,如果PCBC最終需要帶回自行車,那麼發送的自行車就是0,所以應該只需要一個參數就能搞定,我的程式碼是參照柳神的程式碼寫的,我試著按這個想法去改了改程式碼,但是並不能通過,反而改出了bug,然後就放棄了,不知道是我的理解有問題,還是我沒改對,如果有成功的小夥伴希望能戳一下我,謝謝啦!
滿分程式碼
我的程式碼注釋已經很詳細了,應該都能看明白,我就不解釋了,有問題可以在評論指出。
#include <iostream>
#include <algorithm>
#include <climits>
#include <vector>
using namespace std;
// 邊距
int edge[501][501];
// 起點到每個點的最短距離
int dis[501];
// 起點到每個點的最短路徑可能有多個,同一個點就會有多個前驅,我們用vector保存它的所有前驅(都是最短路徑下的前驅)
vector<int> pre[501];
// 各個站點當前容量
// 有個竅門是我們這裡不直接保存它的當前容量,而且保存它的完美容量的差,
// 這樣我們就能很快知道這個站點 缺少 或者 多出 幾輛自行車
int diff[501];
// PCBC需要帶去,或帶回的最少的自行車數
int min_take = ;
// 對應的那個路徑
vector<int> path, temp_path;
// 深度優先遍歷,從PCBC到S有一個或多個最短路徑,比較每種情況下,PCBC最終帶過去或帶回去的自行車最少
// 要求沿途經過的所有站點都要調整到完美狀態
// 因為我們保存的是前驅,所以我們從s往PCBC遍歷,temp_list保存本次路徑
void dfs(int sp) {
// 保存自己
temp_path.push_back(sp);
// 路徑完整了
if (sp == 0) {
// 選擇這個路徑,PCBC最終需要帶回去或帶過來幾輛自行車
int temp_take = 0;
// temp_list裡面是倒著的(如:sp 3 2 1 0),所以我們要倒序遍歷
for (int i = temp_path.size() - 1; i >= 0; --i) {
// 當前站點
int v = temp_path[i];
// 當前站點多出自行車
if (diff[v] > 0) {
temp_take -= diff[v];
} else {
// 當前站點完美或缺少自行車,-diff[i]就是缺的數量
if (temp_take >= -diff[v]) {
// 抵消掉一部分帶回去的,達到完美狀態
temp_take += diff[v]; // diff[i]本身就是負數
} else {
// 不夠抵消,自己缺少 -diff[i],要帶回去的只有temp_back個,
// PCBC還需要帶來-diff[i] - temp_back個,temp_back就=0
temp_take += (-diff[v] - temp_take);
}
}
}
// 選擇本條路徑,PCBC需要帶過來的自行車更少一些,選擇本條路徑
if (abs(min_take) > abs(temp_take)) {
path = temp_path;
min_take = temp_take;
}
// 移除自己,「前呼後應原則」
temp_path.pop_back();
return;
}
// 多個前驅
for (int i = 0; i < pre[sp].size(); ++i) {
// 選擇其中一條
dfs(pre[sp][i]);
}
// 移除自己,「前呼後應原則」
temp_path.pop_back();
return;
}
int main() {
// 初始化邊距
fill(edge[0], edge[0] + 501 * 501, INT_MAX);
// 初始化起點到其他點的最短距離
fill(dis, dis + 501, INT_MAX);
// c每個站點容量,n個城市,s待處理的站點,m是m條邊的距離
// 編號從1開始,P編號0表示PCBC
int c, n, s, m;
scanf("%d %d %d %d", &c, &n, &s, &m);
// 各個站點當前容量
for (int i = 1; i <= n; ++i) {
scanf("%d", &diff[i]);
// 計算與完美狀態的數量差
diff[i] = diff[i] - c / 2;
}
// m條邊
int from, to, d;
while (m-- > 0) {
scanf("%d %d %d", &from, &to, &d);
edge[from][to] = edge[to][from] = d;
}
// Dijstraq求PCBC到每個點的最短距離,並記錄前驅
bool visit[501] = {false};
// 初始化
dis[0] = 0;
// 最短路徑
for (int i = 0; i <= n; ++i) {
int u = -1, min_dis = INT_MAX;
for (int j = 0; j <= n; ++j) {
if (!visit[j] && dis[j] < min_dis) {
u = j;
min_dis = dis[j];
}
}
if (u == -1)
break;
visit[u] = true;
for (int v = 0; v <= n; ++v) {
if (!visit[v] && edge[u][v] != INT_MAX) {
if (dis[u] + edge[u][v] < dis[v]) {
// 更新到v的最短路徑
dis[v] = dis[u] + edge[u][v];
// 更新它的前驅
pre[v].clear();
pre[v].push_back(u);
} else if (dis[u] + edge[u][v] == dis[v]) {
// 多了一條最短路徑就多了一個前驅
pre[v].push_back(u);
}
}
}
}
// 找到了PCBC到全部節點的最短路徑,也找到了這些最短路徑上每個節點的一個或多個直接前驅
// 關注的是從PCBC到s的多個最短路徑中,需要從PCBC帶過去或帶回來的自行車最少的路徑,使用dfs
dfs(s);
// path保存PCBC選擇的最短路徑,min_take需要帶過來的自行車,min_back需要帶回去的自行車
printf("%d 0", min_take > 0 ? min_take : 0);
// temp s 3 2 1 0,需要輸出 0->1->2->3->s
for (int i = path.size() - 2; i >= 0; --i)
printf("->%d", path[i]);
printf(" %d", min_take > 0 ? 0 : -min_take);
return 0;
}


