二分搜索樹看這篇就足夠了

2020 年 5 月 7 日
筆記
數據結構

二分搜索樹(BST):中序遍歷結果為遞增序列

BST是一種特殊的二叉樹，其定義如下：

BST ：在二叉樹的基礎上，任意一個節點滿足大於左子樹中的所有節點，小於右子樹中的所有節點。

注意點：

BST的定義中沒有等號，後續程式碼中可以看到，在插入時，相等的元素會被忽略掉。
BST的中序遍歷結果為遞增序列(應用很廣)，證明：L<node<R;
BST是動態數據結構，即容量會自動擴縮(插入，刪除)。

插入過程:牢記BST的定義,為null時才插入。

private Node add(Node node,E e)：向以node為根節點的BST中插入新的元素e,並返回新的根節點。

private Node add(Node node,E e){
    if(node==null){
        return new Node(e);
    }
    if(e.compareTo(node.e)<0){//左邊插入。其餘不變
        node.left=add(node.left,e);
    }else if(e.compareTo(node.e)){
        node.right=add(node.right,e);
    }
    //相等，忽略。
    return node;
}
public void add(E e){//從根節點開始找。
    
    root=add(root,e);
}

刪除過程(最複雜)：牢記BST的定義，找到時才刪除。

BST的最小值：左子樹的終點，不一定是葉子節點。
BST的最大值：右子樹的終點，不一定是葉子節點。

刪除最小或者最大節點

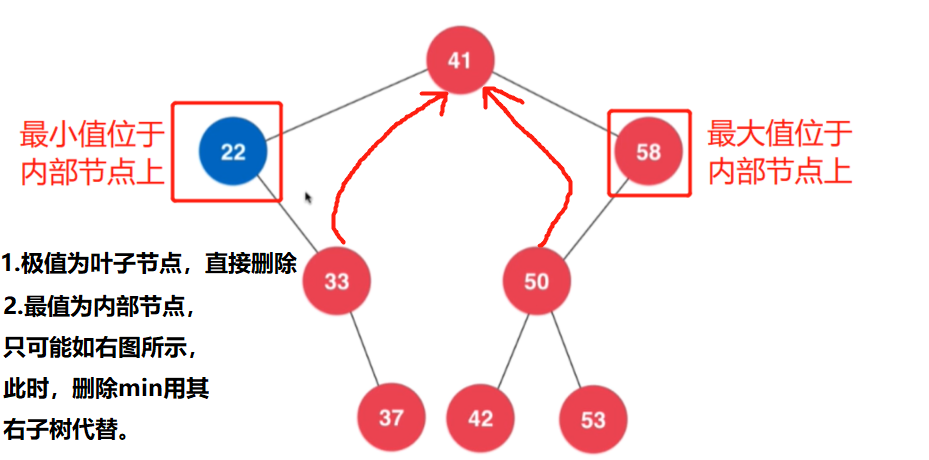
最小值位於節點內部時，其後是一個右子樹，此時刪除節點後，將剩餘子樹接到刪除節點父節點位置，作為他的左子樹。(刪除最大值同理)–滿足BST性質。

private Node removeMin(Node node)刪除已node為根節點的BST的最小節點，並返回刪除節點後新的BST的根節點。

public E removeMin(){
    E min=getMin();
    root=removeMin(root);
    return min;
}
private Node removeMin(Node node){
    //found it,左子樹的終點
    if(node.left==null){
        Node rightNode=node.right;
        size--;
        return rightNode;
    }
    node.left=removeMin(node.left);
    return node;    
}

刪除任意元素

刪除的節點只有右孩子 :刪除當前節點，然後把右子樹放置到當前節點的位置，相當於delMin
刪除節點只有左孩子：刪除當前節點，然後把左子樹放置到當前節點的位置，相等於deMax
待刪除元素左右孩子都有：找到比待刪除節點大的最小節點(BST性質)，用這個節點頂替代刪除節點的位置。

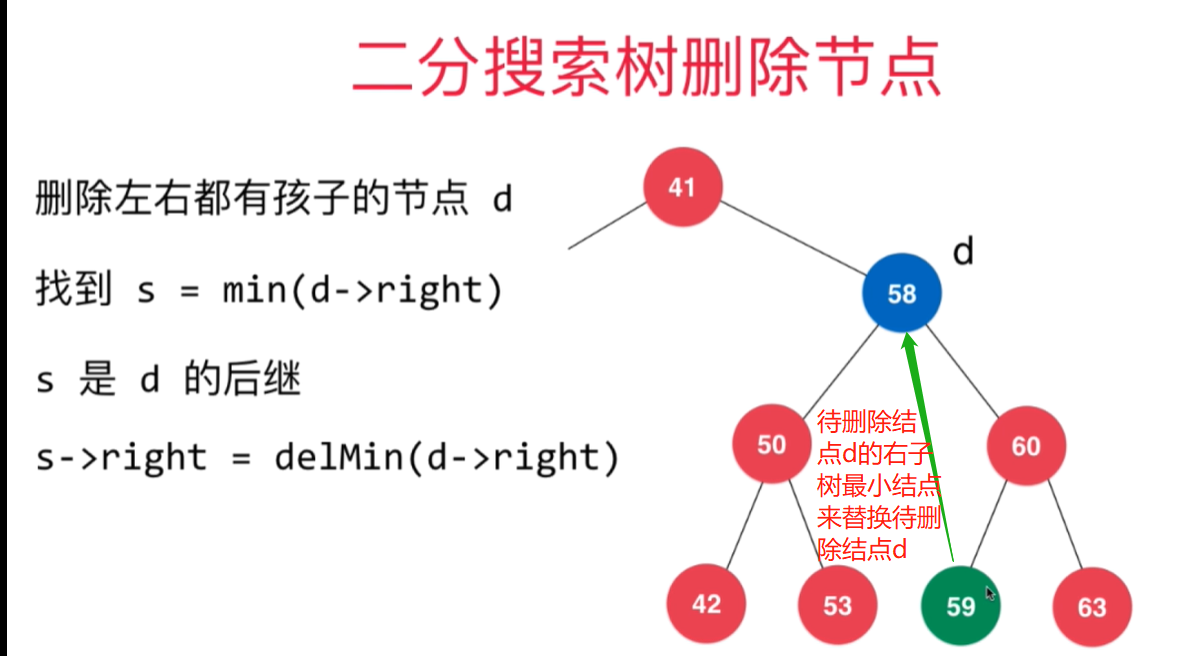
//刪除已node為根的BST中值為e的節點，並返回刪除之後新的BST的根。
private Node remove(Node node,E e){
    if(node==null)return null;
    if(e.comapreTo(node.e)<0){
        node.left=remove(node.left,e);
        return node;
    }
    else if(e.compareTo(node.e)>0){
        node.right=remove(node.right,e);
        return node;
    }
    //找到待刪除元素(e.compareTo(node.e)==0)，體會函數執行到這兒的含義。
    else{
        //待刪除節點左子樹為null
        if(node.left==null){
            Node rightNode=node.right;
            node.right=null;
            size--;
            return rightNode;
        }
        if(node.right==null){
            Node leftNode=node.left;
            node.left=null;
            size--;
          return leftNode;      
        }
        //兩邊都不為null。
        Node successor=minimum(node.right);
        sussessor.right=removeMin(node.right);//右邊最小的。
        sussessor.left=node.right;
        return sussessor;
        
    }
    
}

public void remove(E e) {
    root = remove(root, e);
}

查找元素：BST性質

private boolean contains(Node node,E e){
    if(node==null) return false;
    if(e.compareTo(node.e)<0){
        return contains(node.left,e);
    }else if(e.compareTo(node.e)>0){
        return contains(node.right,e);
    }else{//先找到，這點和刪除的邏輯很像 
        return true;
    }
}
public boolean contains(E e){
    return contains(root,e);
}

BST的完整源碼請點擊這兒

BST缺點：

當插入元素有序時，BST退化為單鏈表。

AVL樹：有序性+平衡性

AVL樹在BST的基礎上增加了平衡性約束。新增的操作(旋轉與高度更新)都是為了滿足平衡性約束

AVL樹中平衡性的定義：

對於任意一個節點，左子樹與右子樹的高度差不能超過1

平衡二叉樹中平衡的意義：

為了保證樹的高度與與節點總數成logN的關係，而一般的操作(add,delete,contains)都與樹的高度有關,例如，堆是完全二叉樹也是平衡二叉樹，對堆的各種操作，時間複雜度都是log(N)

插入：關注第一個不平衡的節點，調整原則是有序性+平衡性

插入就是在失敗的查找的基礎上再操作，插入過程中維持有序性和平衡性的核心操作：旋轉。

我們只需要關注第一個不平衡的節點，然後再遞歸檢查就OK，此時，只需要考察該節點與其孩子節點，其孩子的孩子節點(三代)的關係，因為這是導致不平衡的最小單元。

不平衡情形之一：LL

在節點的左孩子的左側，插入新節點，導致節點失衡，LL，此時通過右旋轉來解決，以中間節點為中心，旋轉，這樣能夠同時滿足有順序性和平衡性。

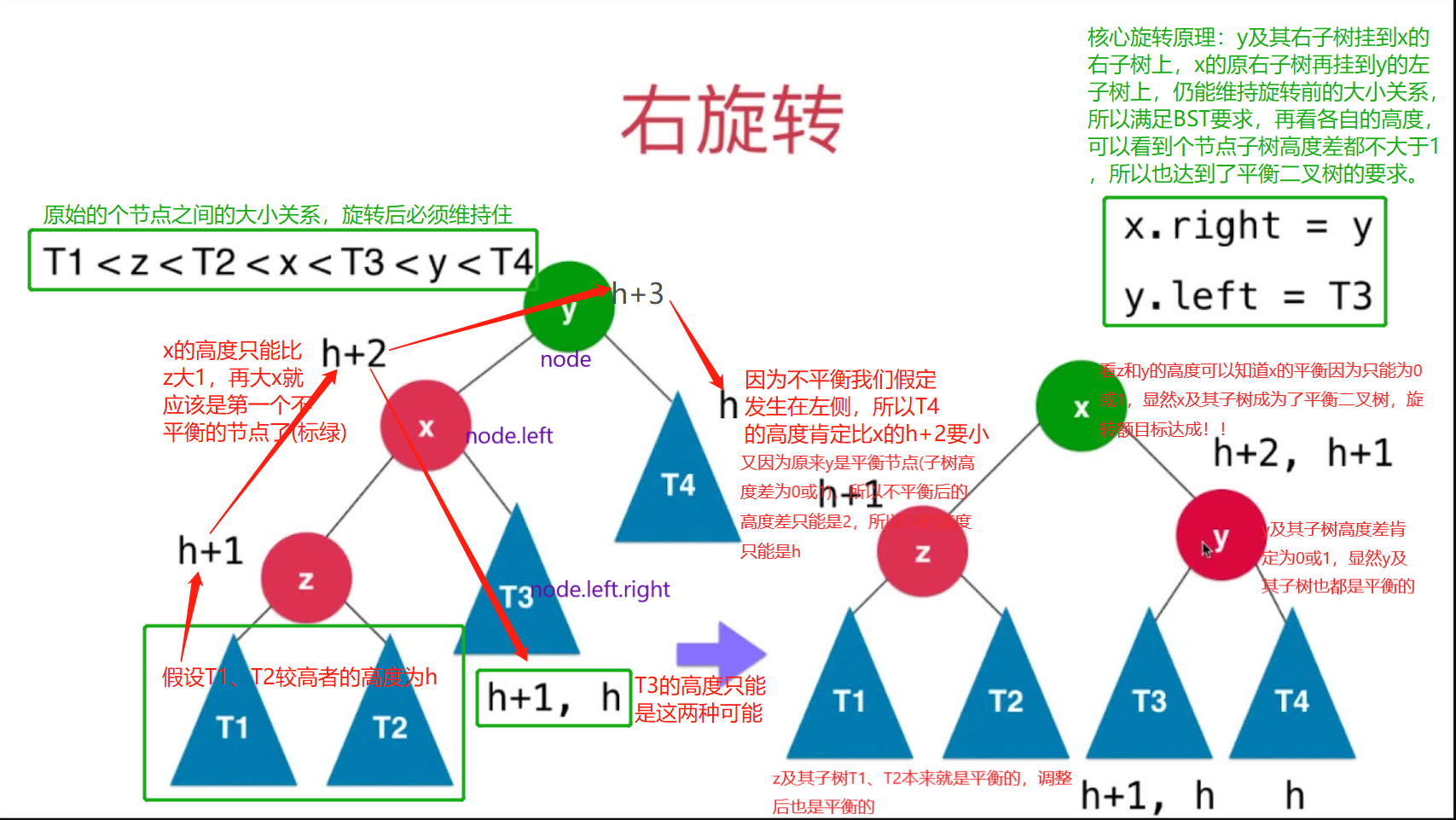
//y:第一個不平衡的節點，返迴旋轉後的根節點x
private Node rotateRight(Node y ){
    Node x=y.left;
    Node T3=x.right;
    x.right=y;
    y.left=T3;
    //對x和y的位置進行調整，相應的高度也需要更新！！
    y.height=calHeight(y);
    x.height=calHeight(x);
    return x;
}
private Node add(Node node,K key, V va){
    //LL:在node的左側的左側添加的節點導致node不平衡。
    if(balance>1&&calBalance(node,left)>=0){//calBalance:left的高度-right高度
 		return rotateRight(node);       
    }
}

不平衡情形之二：RR

在節點的右側的右側加入新節點，導致節點失衡，RR,採用左旋轉解決，旋轉中心為中間節點x.

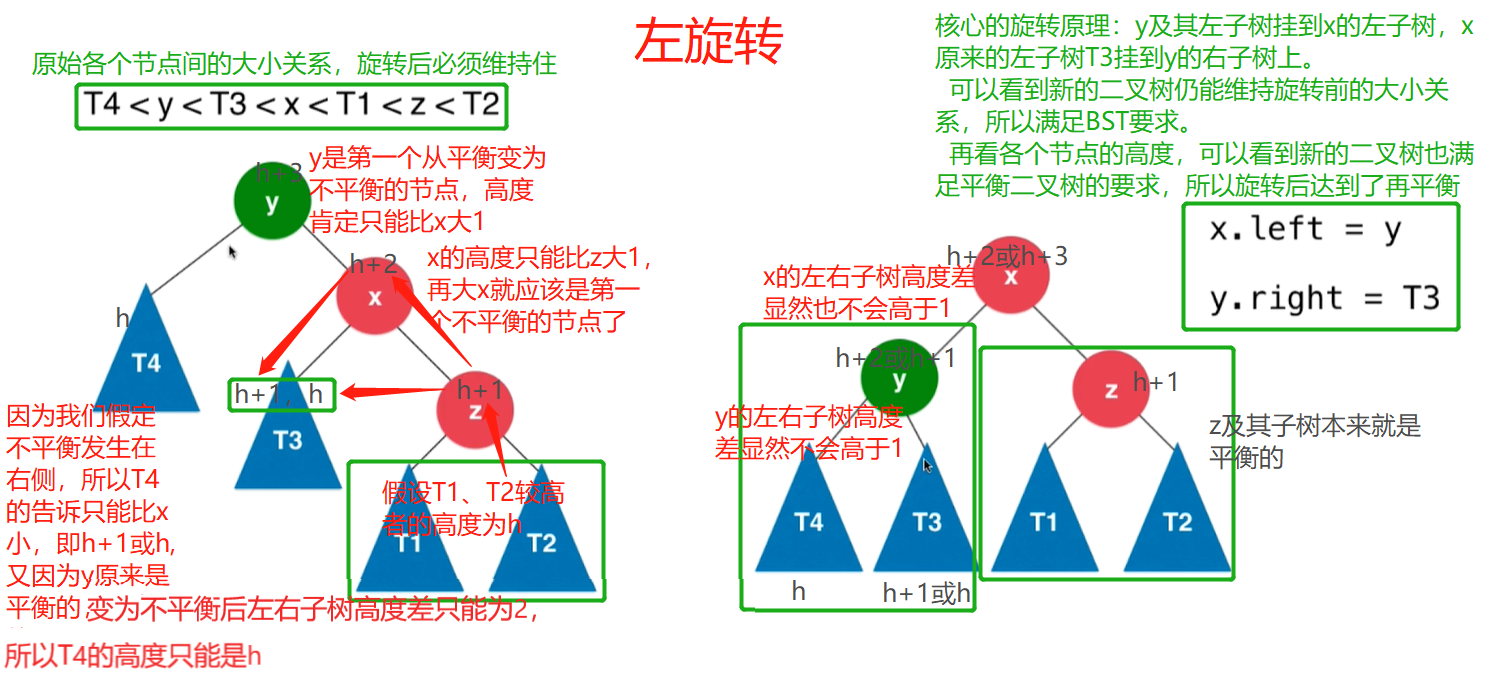
//y是第一個失衡的節點，返迴旋轉後的根節點
private Node rotateLeft(Node y){
    Node x=y.right;
    Node T3=x.left;
    x.left=y;
    y.right=T3;
    //更新高度
    x.height=calHeight(x);
    y.height=calHeight(y);
    return x;   
}
private Node add(Node node, K key,V val){
    //....
    if(balance<-1&&calBalance(node.right)<=0){//balance的定義L-R
        return rotateLeft(node);
    }
}

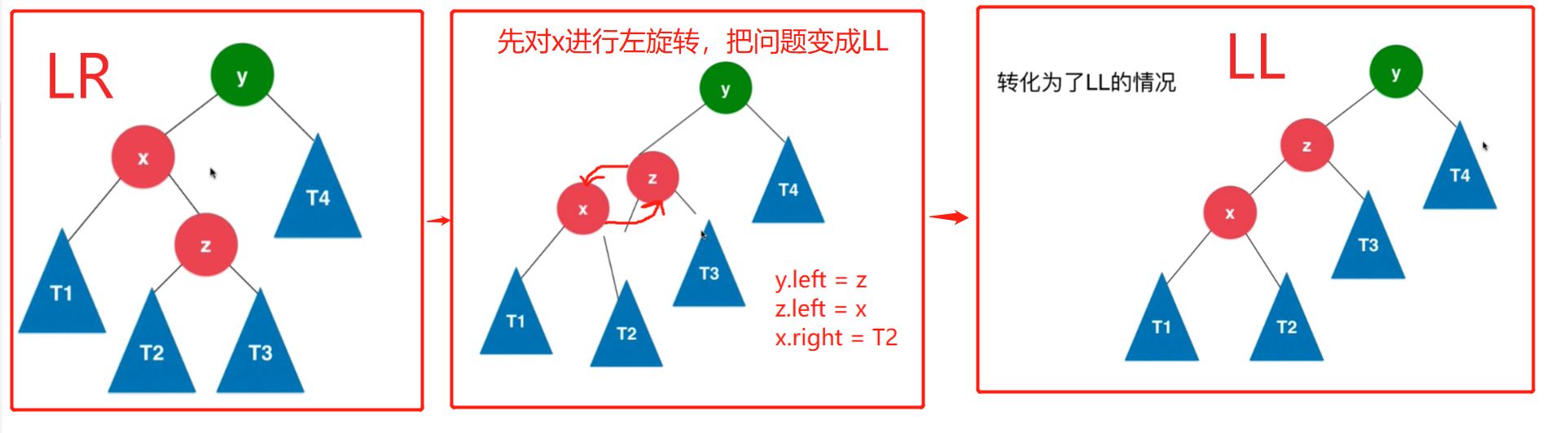
不平衡情形三：LR

在節點左孩子的右側加入新節點(LR),導致AVL樹失衡，調整方式：先左旋轉(LL)後右旋轉

private Node add(Node node,K key ,V val){//牢記要滿足有序性+平衡性
    //....
    if(balance>1&&calBalance(node.left)<0){//以Z為中心。
        node.left=rotateLeft(node.left);
        return rotateRight(node);
    }
    //....
}

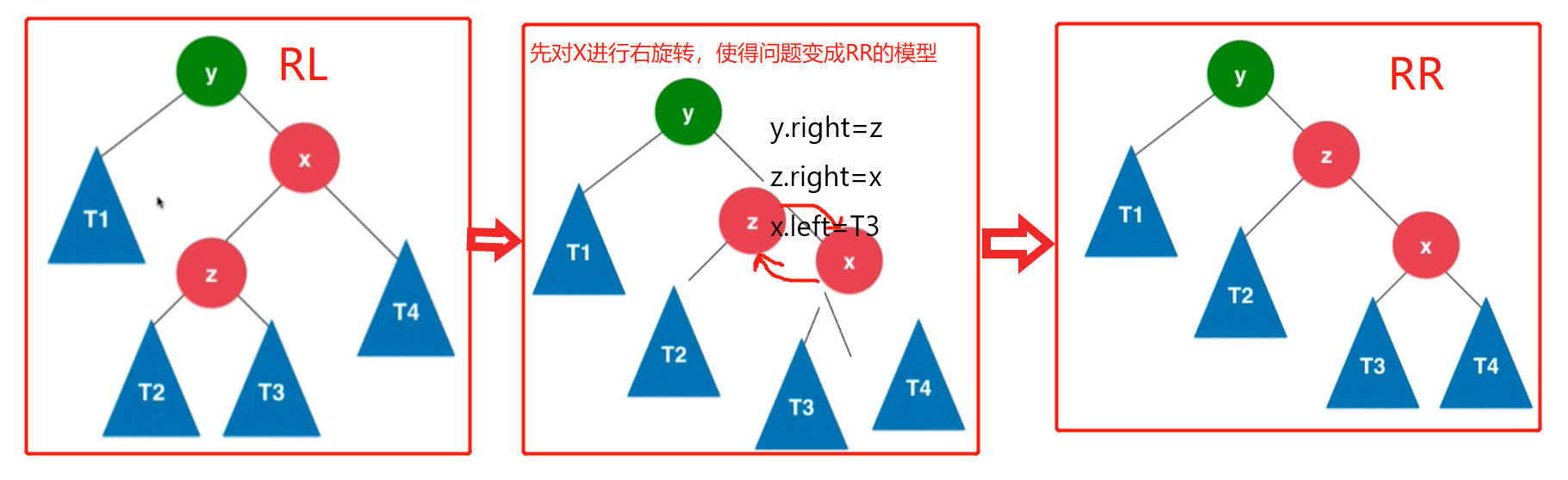
不平衡情形三：RL(上一種情形的對稱）

在節點右孩子的左側插入新節點導致樹失衡，RL.調整方式：先右旋轉(RR)後左選擇.

private Node add(Node node,K key ,V val){
    //*...
    if(balance<-1&&calBalance(Node.right)>0){
        node.right=rotateRight(node.right);//z為中心。
        return rotateLeft(node);
    }
    //....
}

刪除：在BST(有序)的基礎上再加入旋轉操作。

BST的刪除操作已經保證有序性了，再此基礎上還需要考慮LL,LR,RR,RL著四種不平衡狀態。

public V remove(K key){
    Node node=getNode(root,key);
    if(node!=null){
        root=reomve(root,key);
        return node.val;
    }
    return null;
}
private Node remove(Node node , K key){
//程式碼與BST的刪除邏輯完全一樣，只是為了調整平衡性，用retNode來保存刪除後的頭結點。
    
    return rotateToReBalance(retNode);
}

//判斷當前節點是否需要旋轉，並執行相應的旋轉操作。
private Node rotateToReBalance(Node node){
    if(node==null) return null;
    node.height=calHeight(node);
    int blc=calBalance(node);
    if(blc>1&&calBlanece(node.left)>=0){
        return rotateRight(node);
    }
    if(blc<-1&&calBalance(node.right)<=0){
        return rotateLeft(node);
    }
    if(blc>1&&calBalance(node.left)<0){
        node.left=rotateLeft(node.left);
        return rotateRight(node);
    }
    if(blc<-1&&calBalance(node.right)>0){
        node.right=rotateRight(node.right);
        return rotateLeft(node);
    }
    //不需要維護平衡，
    return node;
}

AVL樹的完整源碼請點擊這兒

AVL樹缺點

平衡條件過於苛刻。
插入和刪除的過程都需要驗證平衡性(LL,RR,LR,RL)

基於AVL樹的Set和Map。

紅黑樹：與2-3樹是等價的

定義：

每個節點或者為紅色、或者為黑色。
根節點為黑色。
每個葉子節點(最後的空節點)是黑色的，即null是黑色的，空樹也是紅黑樹。
如果一個節點是紅色的，那麼他的孩子節點都是黑色的。
從任意一個節點到葉子節點，經過的黑色節點數相同。

2-3樹,一種特殊的B樹，即m=3.

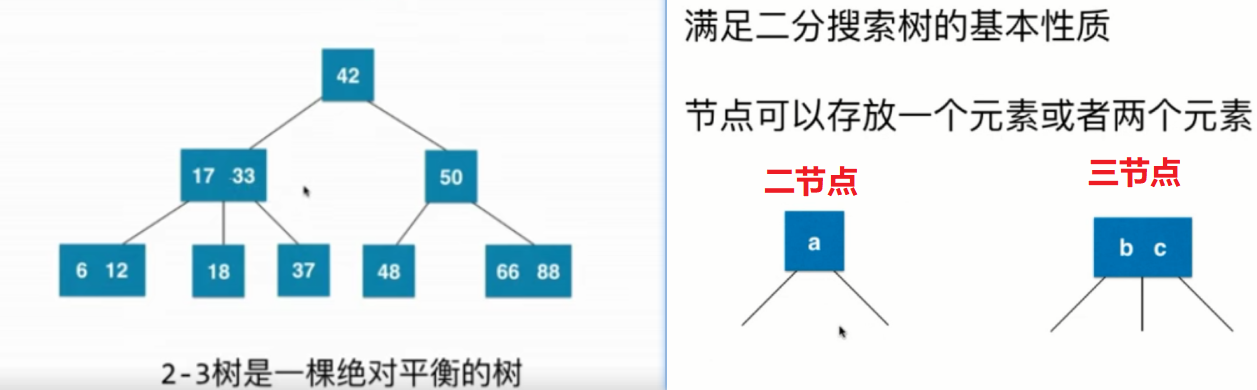
2-3樹滿足BST的基本性質(有序性)，節點可以存放一個元素(二節點)，也可以存放兩個元素(三節點)。

性質：2-3樹是一顆絕對平衡的樹。從根節點到任意葉子節點之間具有相同的節點數。

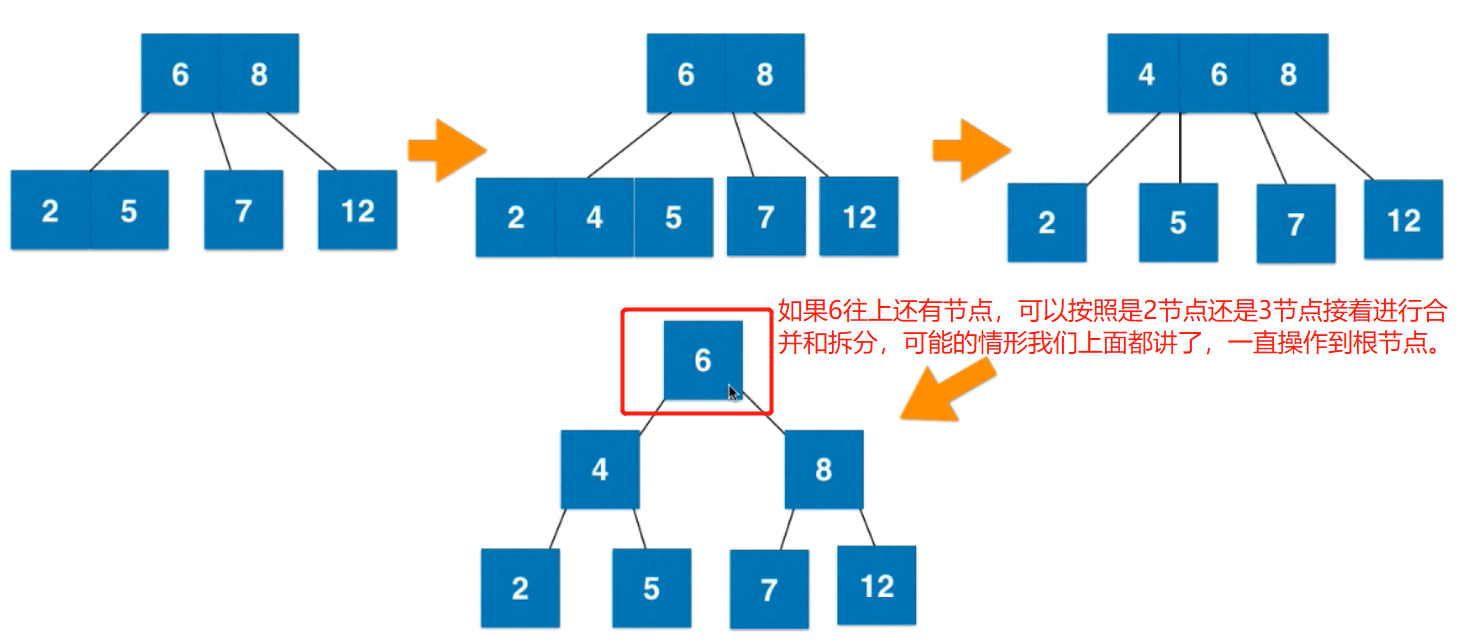
2-3的插入：與最後找到的葉子節點進行融合。

2-3樹的插入過程就是不斷形成3節點(則原來是2節點)、4節點(有4個分叉，即3個元素)的過程，然後拆分4節點為三個2節點的過程。目的：滿足2-3絕對平衡的性質。

2-3樹與紅黑樹的等價性

用單個黑色節點表示2-3樹中的2節點
用紅節點+父節點(顏色為黑)表表示2-3樹的3節點，每個3節點會對應一個紅節點,紅色節點左傾。

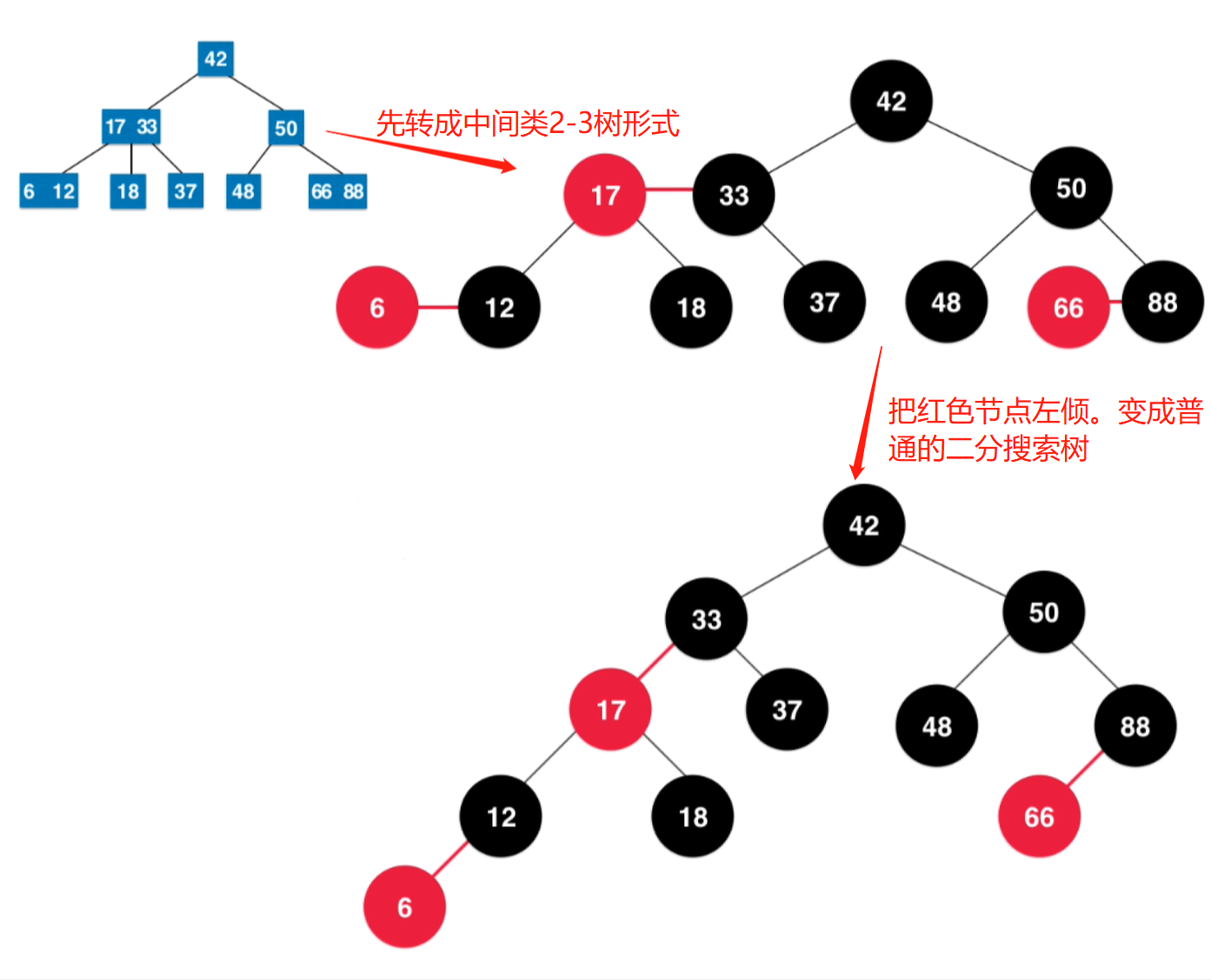
紅黑樹的插入(與2-3樹類比)

當向2節點插入時，帶插入位置是左節點，則不調整，是右節點則需要左旋轉+顏色翻轉，以滿足紅黑樹的定義。

左旋轉過程如下

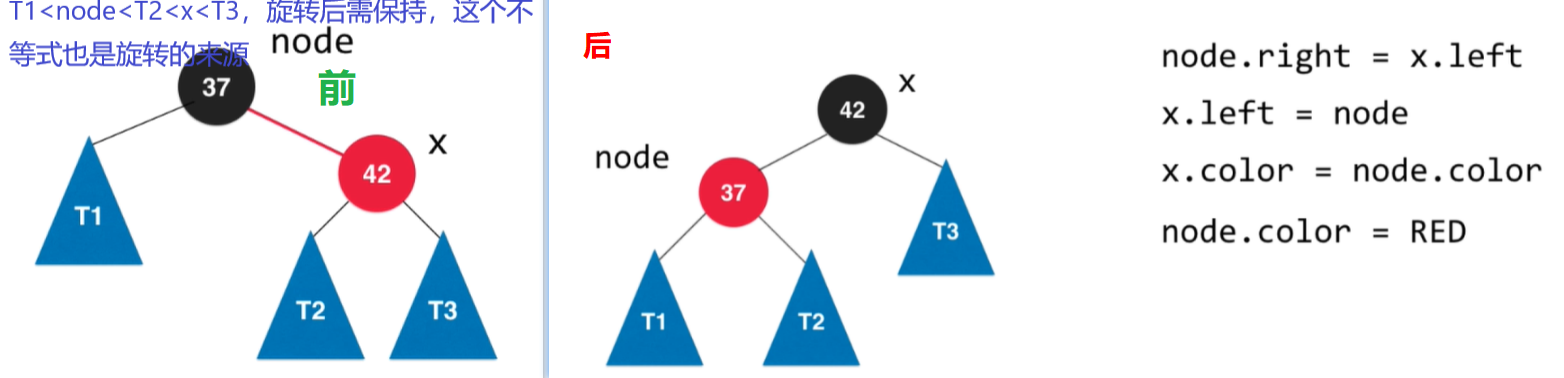
private Node rotateLeft(Node node) {
    // 暫存節點
    Node x = node.right;
    // 左旋轉
    node.right = x.left;
    x.left = node;
    // 更新顏色
    x.color = node.color;
    node.color = RED;
    return x;
}

private Node rotateRight(Node node) {
    // 暫存節點
    Node x = node.left;
    Node T1 = x.right;
    // 右旋轉
    node.left = T1;
    x.right = node;
    // 顏色更新
    x.color = node.color;
    node.color = RED;
    return x;
}

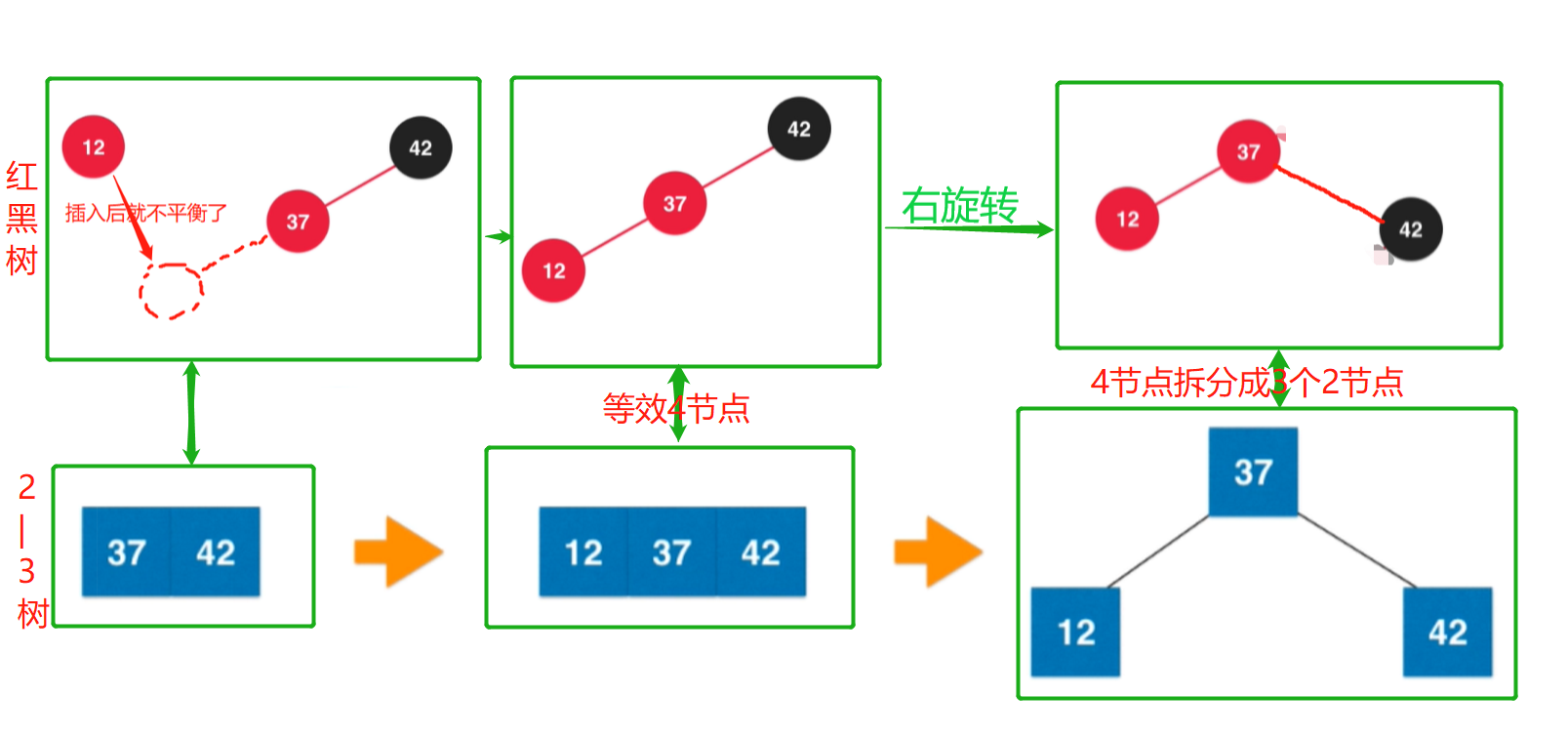
當向3節點插入時，需要依次經過左旋轉，右旋轉，顏色翻轉等過程。
紅黑樹的源碼請點擊這兒

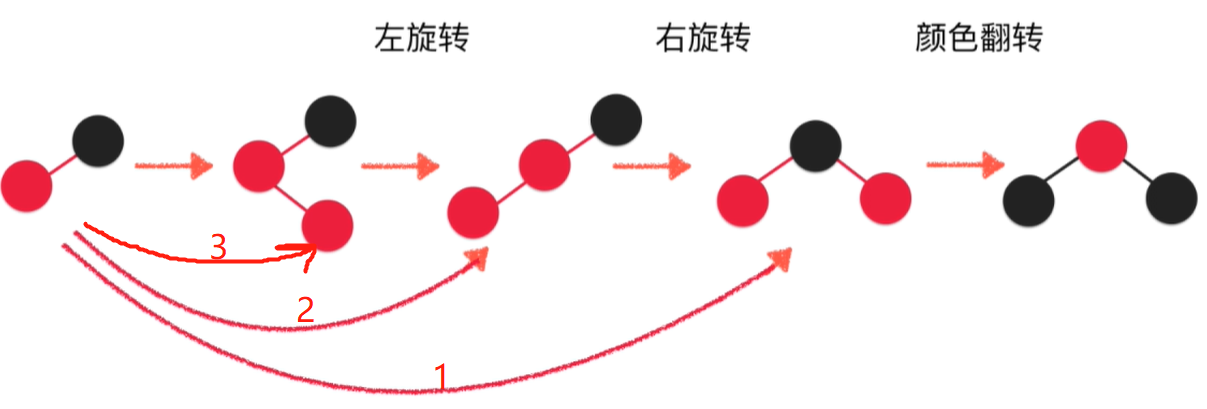
紅黑樹的統計性能更優

綜合增刪改查所有的操作，紅黑樹是平均性能最好的。AVL樹的插入和刪除過於複雜，查詢較多時，AVL樹比較合適。普通的BST對於有序數據就退化為鏈表。

紅黑樹更多

伸展樹:考慮局部性原理的BST。
JDK中的TreeMap和TreeSet就是基於紅黑樹實現的。

Tags: 數據結構