9.隊列:生產者消費者模式
隊列:生產消費模式及執行緒池的運用
關注公眾號 MageByte,設置星標獲取最新乾貨。 「加群」 進入技術交流群獲更多技術成長。
向固定大小的執行緒池投放請求任務時,若果執行緒池中沒有空閑資源了,這時候還有新的請求進來,執行緒池如何處理這個請求?拒絕請求還是排隊?使用怎樣的處理機制
一般兩種策略:
- 直接拒絕任務請求;
- 將請求排隊,等有空閑執行緒的時候取出排隊的請求繼續處理。
那如何存儲排隊的請求呢?這就是今天要講的話題。
其底層的數據結構就是今天我們要講的內容,「隊列」Queue。
完整程式碼詳見 GitHub://github.com/UniqueDong/algorithms.git
什麼是隊列
用一個生活例子,可以想像成超市排隊結賬,先來的先結賬,後面的人只能站在末尾,不允許插隊。先進先出,這就是所謂的「隊列」
隊列是一種線性數據結構,隊列的出口端叫「隊頭」,隊列的入口端叫「隊尾」。
與棧類似隊列的數據結構可以使用數組實現也可以使用鏈表實現。關於棧的內容同學們可以翻閱歷史文章學習「棧:實現瀏覽器前進後退」,隊列最基本的操作也是兩個:入隊 (enqueue) ,將新元素放到隊尾;出隊 (dequeue),從隊頭移除元素,出隊元素的下一個元素變成新的隊頭。
作為基礎的數據結構,隊列的應用也很廣泛,尤其是一些特定場景下的隊列。比如循環隊列、阻塞隊列、並發隊列。它們在很多偏底層系統、框架、中間件的開發中,起著關鍵性的作用。比如高性能隊列 Disruptor、Linux 環形快取,都用到了循環並發隊列;Java concurrent 並發包利用 ArrayBlockingQueue 來實現公平鎖等。
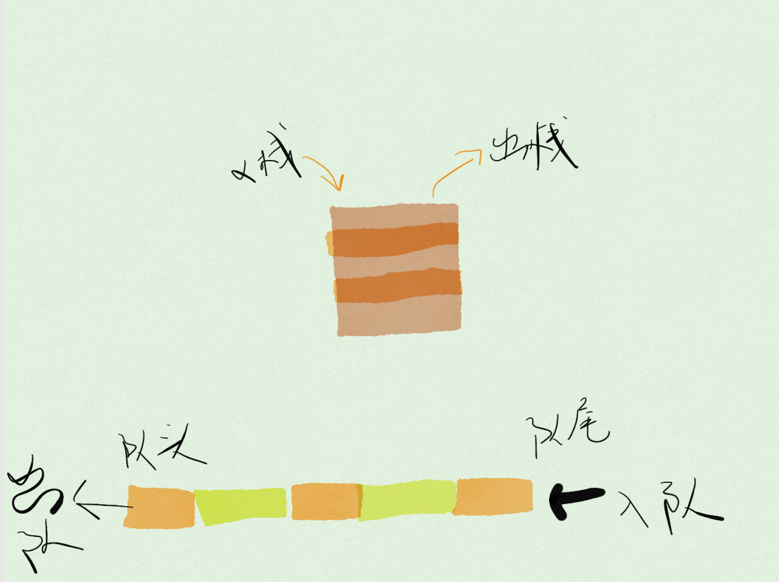
隊列也是一種操作受限的線性表數據結構。
順序隊列與鏈式隊列
隊列是跟棧一樣,是一種抽象的數據結構。 具有先進先出的特性,在隊頭刪除數據,在隊尾插入數據。
可以使用數組實現,也可以使用鏈表實現。使用數組實現的叫 順序隊列,用鏈表實現的 叫 鏈式隊列。
順序隊列
一起先來看數組實現的隊列:
- 出隊操作就是把元素移除隊列,只允許在隊頭移除,出隊的下一個元素成為新的隊頭。
- 入隊操作就是把新元素放入隊列,只允許在隊尾插入,新元素的的下一個位置成為隊尾。
隨著不停地進行入隊、出隊操作,head 和 tail 都會持續往後移動。當 tail 移動到最右邊,即使數組中還有空閑空間,也無法繼續往隊列中添加數據了。這個問題該如何解決呢?
當出現這種情況的時候我們就需要做數據遷移。如圖所示:當 abcd 入隊後,對應的指針位置。
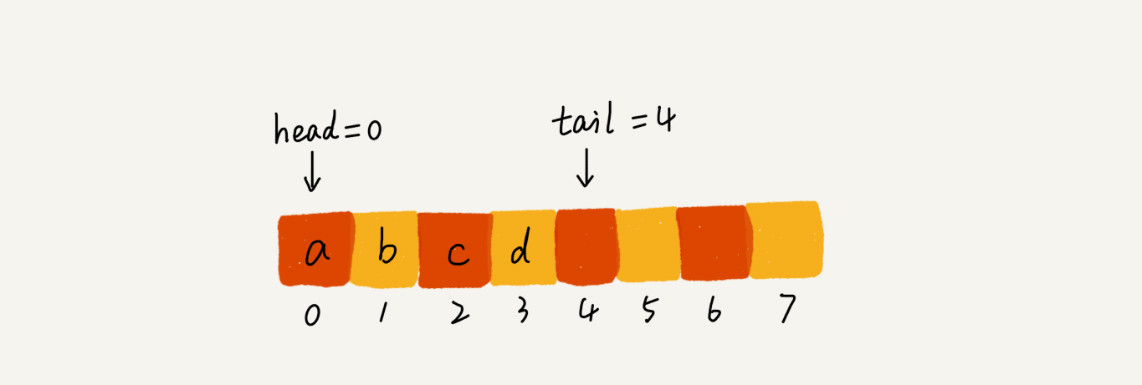
現在我們執行出隊操作
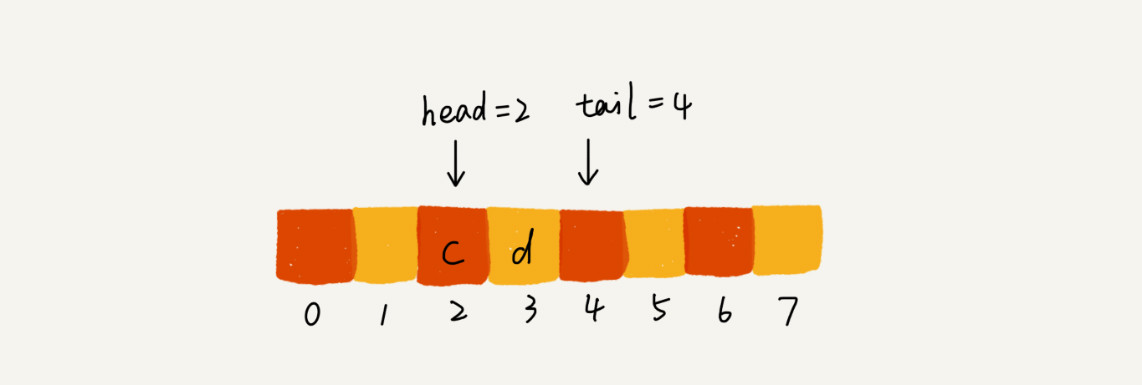
當我們調用兩次出隊操作之後,隊列中 head 指針指向下標為 2 的位置,tail 指針仍然指向下標為 4 的位置。
遷移操作其實就是把整段數據移動到數組 0 開始的位置。
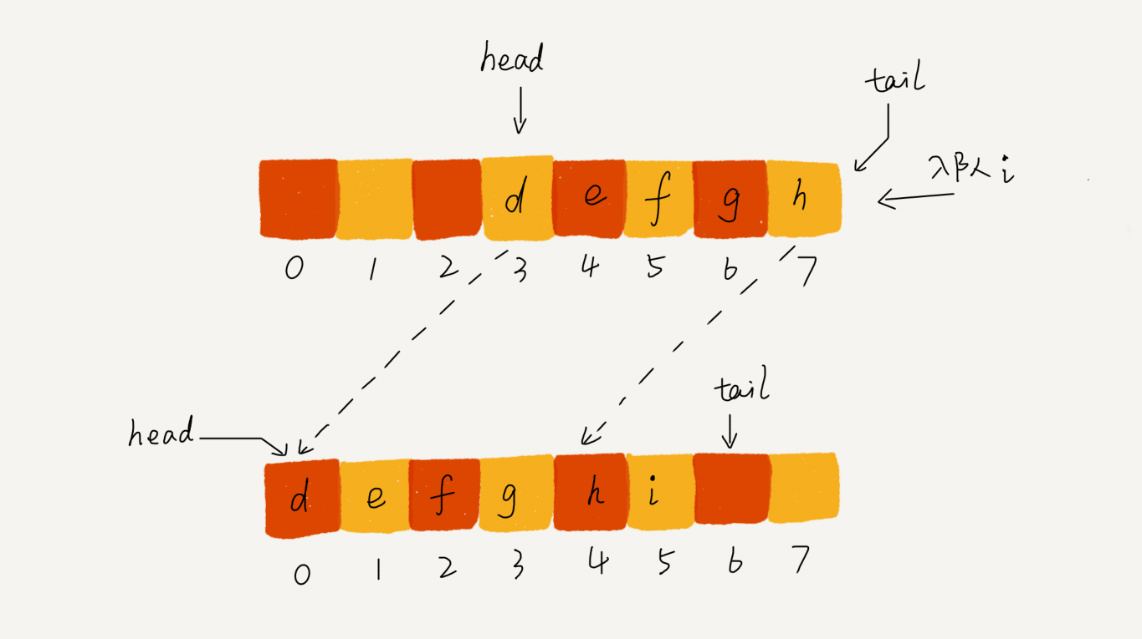
具體程式碼如下
/**
* 數組實現隊列
*/
public class ArrayQueue<E> extends AbstractQueue<E> {
/**
* The queued items
*/
final E[] items;
/**
* 隊頭指針
*/
private int front;
/**
* 隊尾指針
*/
private int rear;
/**
* Creates an ArrayQueue with the given capacity
*
* @param capacity the capacity of this queue
*/
public ArrayQueue(Class<E> type, int capacity) {
if (capacity <= 0) {
throw new IllegalArgumentException();
}
this.items = (E[]) Array.newInstance(type, capacity);
}
public int capacity() {
return items.length;
}
@Override
public E dequeue() {
if (front == rear) {
throw new IllegalStateException("Queue empty");
}
return items[front++];
}
@Override
public boolean enqueue(E e) {
if (isFull()) {
throw new IllegalStateException("Queue empty");
}
// 隊尾沒有空間了,需要執行數據遷移
if (rear == capacity()) {
// 數據遷移
if (rear - front >= 0) {
System.arraycopy(items, front, items, 0, rear - front);
}
// 調整 front 與 rear
rear -= front;
front = 0;
}
items[rear++] = e;
return true;
}
@Override
public boolean isFull() {
return rear == capacity() && front == 0;
}
@Override
public boolean isEmpty() {
return front == rear;
}
}
鏈式隊列
我們可以通過之前學習過的鏈表來實現隊列,具體詳見單向鏈表篇 。其實主要就是利用了 出隊就是鏈表頭刪除數據,入隊就是尾節點添加數據
public class LinkedQueue<E> extends AbstractQueue<E> implements Queue<E> {
private final SingleLinkedList<E> linkedList;
public LinkedQueue() {
this.linkedList = new SingleLinkedList<>();
}
@Override
public E dequeue() {
if (linkedList.isEmpty()) {
throw new IllegalStateException("Queue empty");
}
return linkedList.remove();
}
@Override
public boolean enqueue(E e) {
return linkedList.add(e);
}
@Override
public boolean isFull() {
return false;
}
@Override
public boolean isEmpty() {
return linkedList.isEmpty();
}
}
循環隊列
剛剛的例子,當 rear == capacity 的時候,會出現數據遷移操作,這樣性能受到影響,那如何避免呢?
原本數組是有頭有尾的,是一條直線。現在我們把首尾相連,扳成了一個環。
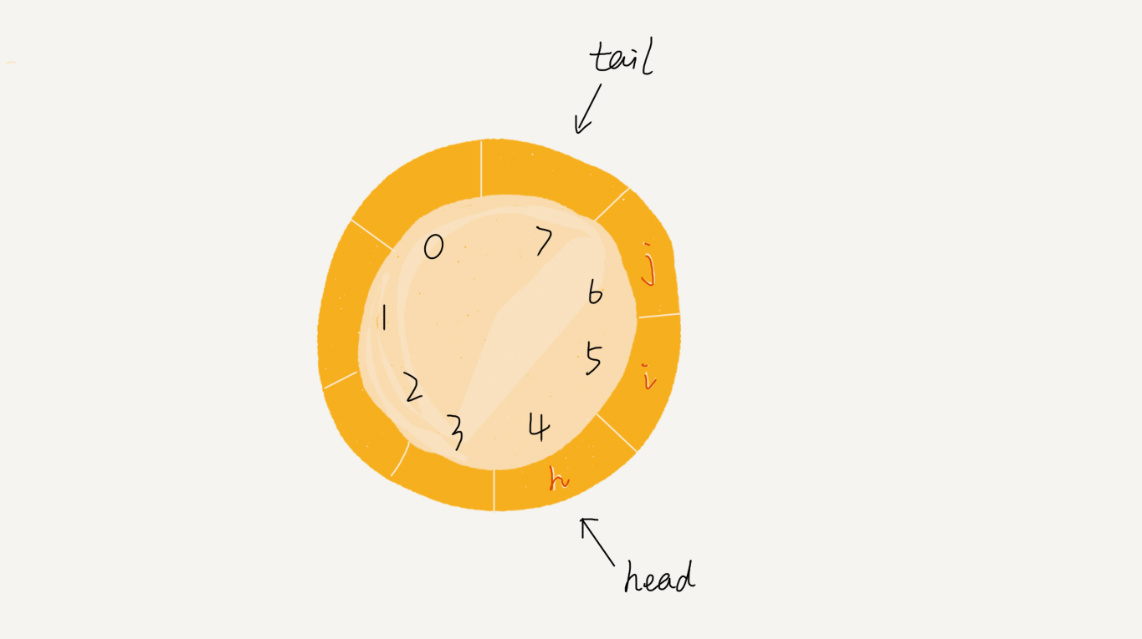
我們可以看到,圖中這個隊列的大小為 8,當前 head=4,tail=7。當有一個新的元素 a 入隊時,我們放入下標為 7 的位置。但這個時候,我們並不把 tail 更新為 8,而是將其在環中後移一位,到下標為 0 的位置。當再有一個元素 b 入隊時,我們將 b 放入下標為 0 的位置,然後 tail 加 1 更新為 1。所以,在 a,b 依次入隊之後,循環隊列中的元素就變成了下面的樣子:
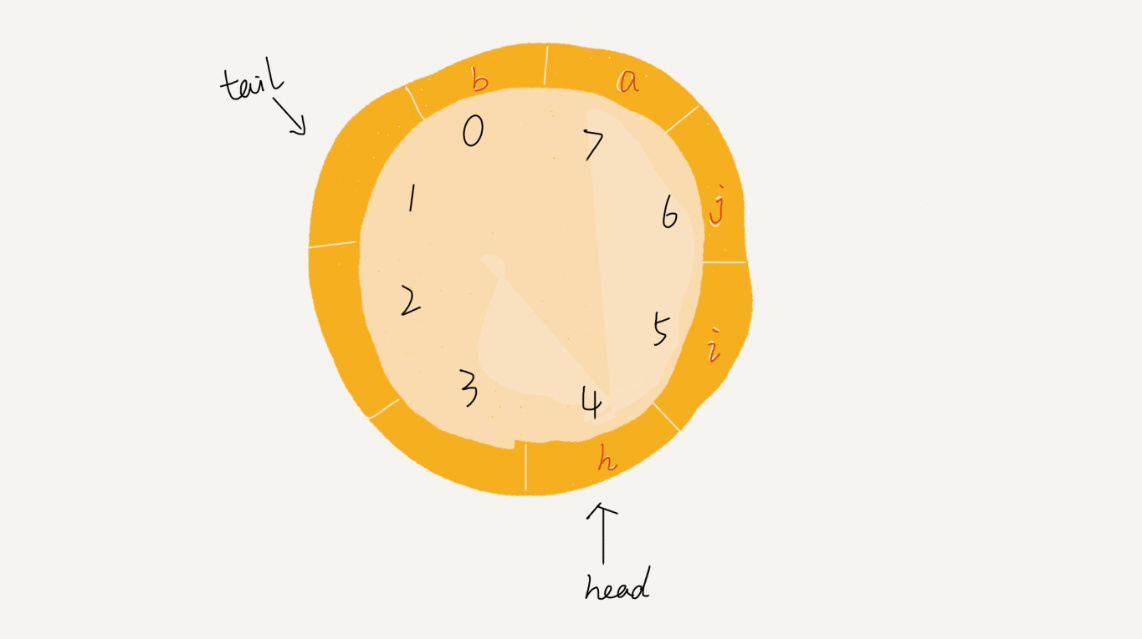
隊列為空的判斷依然是 front == rear,隊列滿的條件則是 (rear + 1) % capacity = front
你有沒有發現,當隊列滿時,圖中的 tail 指向的位置實際上是沒有存儲數據的。所以,循環隊列會浪費一個數組的存儲空間。
/**
* 數組實現環形隊列
*
* @param <E>
*/
public class ArrayCircleQueue<E> extends AbstractQueue<E> {
/**
* The queued items
*/
final E[] items;
/**
* 隊頭指針
*/
private int front;
/**
* 隊尾指針
*/
private int rear;
public int capacity() {
return items.length;
}
/**
* Creates an ArrayQueue with the given capacity
*
* @param capacity the capacity of this queue
*/
public ArrayCircleQueue(Class<E> type, int capacity) {
if (capacity <= 0) {
throw new IllegalArgumentException();
}
this.items = (E[]) Array.newInstance(type, capacity);
}
@Override
public E dequeue() {
if (front == rear) {
throw new IllegalStateException("Queue empty");
}
E item = items[front];
front = (front + 1) % items.length;
return item;
}
@Override
public boolean enqueue(E e) {
checkNotNull(e);
int newRear = (rear + 1) % items.length;
if (newRear == front) {
throw new IllegalStateException("Queue full");
}
items[rear] = e;
this.rear = newRear;
return true;
}
@Override
public boolean isFull() {
return (rear + 1) % items.length == front;
}
@Override
public boolean isEmpty() {
return rear == front;
}
}

推薦閱讀
4.線性表之數組
5.鏈表導論-心法篇
7.雙向鏈表正確實現
原創不易,覺得有用希望隨手「在看」「收藏」「轉發」三連。

