python實現樸素貝葉斯
什麼是樸素貝葉斯?
樸素貝葉斯是jiyu貝葉斯定理和特徵條件獨立假設的分類方法。即對於給定訓練數據集,首先基於特徵條件獨立假設學習輸入\輸出的聯合概率分布,然後基於此模型,對於給定的輸入x,利用貝葉斯定理求出後驗概率最大的輸出y。
什麼是貝葉斯法則?

在貝葉斯法則中,每個名詞都有約定俗成的名稱:
Pr(A)是A的先驗概率或邊緣概率。之所以稱為”先驗”是因為它不考慮任何B方面的因素。
Pr(A|B)是已知B發生後A的條件概率,也由於得自B的取值而被稱作A的後驗概率。
Pr(B|A)是已知A發生後B的條件概率,也由於得自A的取值而被稱作B的後驗概率。
Pr(B)是B的先驗概率或邊緣概率,也作標準化常量(normalized constant)。
按這些術語,Bayes法則可表述為:
後驗概率 = (似然度 * 先驗概率)/標準化常量 也就是說,後驗概率與先驗概率和似然度的乘積成正比。
另外,比例Pr(B|A)/Pr(B)也有時被稱作標準似然度(standardised likelihood),Bayes法則可表述為:
後驗概率 = 標準似然度 * 先驗概率。
什麼是條件獨立性假設?

也就是Z事件發生時,X事件是否發生與Y無關,Y事件是否發生與X事件無關。
什麼是聯合概率分布?
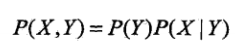
如何由聯合概率模型得到樸素貝葉斯 模型?
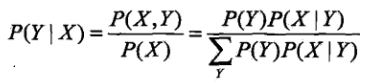
樸素貝葉斯參數估計:極大似然估計

樸素貝葉斯演算法描述:

具體例子:


極大似然估計存在的問題?

使用貝葉斯估計求解上述問題?

程式碼實現:
from __future__ import division, print_function import numpy as np import math from mlfromscratch.utils import train_test_split, normalize from mlfromscratch.utils import Plot, accuracy_score class NaiveBayes(): """The Gaussian Naive Bayes classifier. """ def fit(self, X, y): self.X, self.y = X, y self.classes = np.unique(y) self.parameters = [] # Calculate the mean and variance of each feature for each class for i, c in enumerate(self.classes): # Only select the rows where the label equals the given class X_where_c = X[np.where(y == c)] self.parameters.append([]) # Add the mean and variance for each feature (column) for col in X_where_c.T: parameters = {"mean": col.mean(), "var": col.var()} self.parameters[i].append(parameters) def _calculate_likelihood(self, mean, var, x): """ Gaussian likelihood of the data x given mean and var """ eps = 1e-4 # Added in denominator to prevent division by zero coeff = 1.0 / math.sqrt(2.0 * math.pi * var + eps) exponent = math.exp(-(math.pow(x - mean, 2) / (2 * var + eps))) return coeff * exponent def _calculate_prior(self, c): """ Calculate the prior of class c (samples where class == c / total number of samples)""" frequency = np.mean(self.y == c) return frequency def _classify(self, sample): """ Classification using Bayes Rule P(Y|X) = P(X|Y)*P(Y)/P(X), or Posterior = Likelihood * Prior / Scaling Factor P(Y|X) - The posterior is the probability that sample x is of class y given the feature values of x being distributed according to distribution of y and the prior. P(X|Y) - Likelihood of data X given class distribution Y. Gaussian distribution (given by _calculate_likelihood) P(Y) - Prior (given by _calculate_prior) P(X) - Scales the posterior to make it a proper probability distribution. This term is ignored in this implementation since it doesn't affect which class distribution the sample is most likely to belong to. Classifies the sample as the class that results in the largest P(Y|X) (posterior) """ posteriors = [] # Go through list of classes for i, c in enumerate(self.classes): # Initialize posterior as prior posterior = self._calculate_prior(c) # Naive assumption (independence): # P(x1,x2,x3|Y) = P(x1|Y)*P(x2|Y)*P(x3|Y) # Posterior is product of prior and likelihoods (ignoring scaling factor) for feature_value, params in zip(sample, self.parameters[i]): # Likelihood of feature value given distribution of feature values given y likelihood = self._calculate_likelihood(params["mean"], params["var"], feature_value) posterior *= likelihood posteriors.append(posterior) # Return the class with the largest posterior probability return self.classes[np.argmax(posteriors)] def predict(self, X): """ Predict the class labels of the samples in X """ y_pred = [self._classify(sample) for sample in X] return y_pred
這裡實現的是高斯貝葉斯估計,具體原理可參考://zhuanlan.zhihu.com/p/64498790
接著是主運行:
from __future__ import division, print_function from sklearn import datasets import numpy as np import sys sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/") from mlfromscratch.utils import train_test_split, normalize, accuracy_score, Plot from mlfromscratch.supervised_learning import NaiveBayes def main(): data = datasets.load_digits() X = normalize(data.data) y = data.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4) clf = NaiveBayes() clf.fit(X_train, y_train) y_pred = clf.predict(X_test) accuracy = accuracy_score(y_test, y_pred) print ("Accuracy:", accuracy) # Reduce dimension to two using PCA and plot the results Plot().plot_in_2d(X_test, y_pred, title="Naive Bayes", accuracy=accuracy, legend_labels=data.target_names) if __name__ == "__main__": main()
運行結果:
Accuracy: 0.9122562674094707
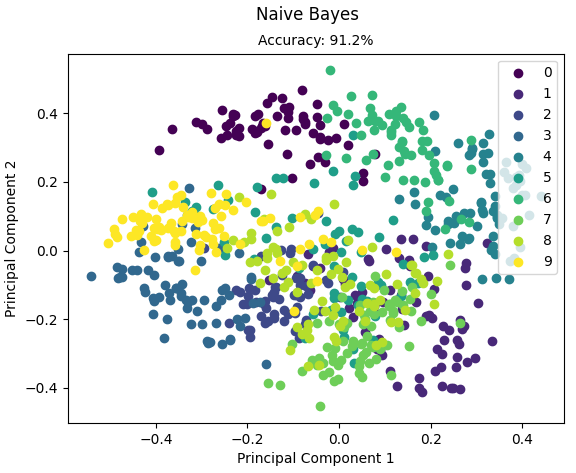
程式碼來源://github.com/eriklindernoren/ML-From-Scratch
參考:
百度百科
//blog.csdn.net/qiu_zhi_liao/article/details/90671932
統計學習方法

