手寫實現java棧結構,並實現簡易的計算器(基於後綴演算法)
一、定義
棧是一種線性表結構,棧結構中有兩端,對棧的操作都是對棧的一端進行操作的,那麼被操作的一端稱為棧頂,另一端則為棧底。對棧的操作其實就是只有兩種,分別是入棧(也稱為壓棧)和出棧(也稱為彈棧)。入棧,將新元素壓入棧中,那麼此時這個棧元素就成為了棧頂元素,棧深度相應的+1。出棧,將棧中的棧頂元素彈出來,此時棧頂的下一個元素就會成為新的棧頂元素,棧深度也相應的-1。根據入棧和出棧的規則,也可以得到棧數據的順序是後進先出(LIFO,LAST IN FIRST OUT)的特性。棧結構的效率是非常高的,因此無論棧中數據的量有多大,操作的也只有棧頂元素一個數據,因此棧的時間複雜度為O(1),這裡不考慮棧溢出擴容的問題。棧結構示意圖下圖:

二、棧的應用場景
棧的數據介面在編程中的應用是非常廣泛的,其中包括:
1、瀏覽器頁面的瀏覽記錄。我們在瀏覽器中瀏覽的頁面的時候後退和前進能夠正確的跳轉到對應的頁面,就是利用了棧的特性來實現的。
2、java虛擬機中棧的操作數棧也是利用棧實現的。java在編譯的時候講操作的程式碼壓入操作數棧中,進行運算時就將棧頂元素彈出來,然後進行運算後將結果再壓進操作數棧中。
3、計算器的實現。我們在計算的時候一般都是從左往右計算的,但是這種方式對於電腦是非常不友好的,它需要進行大量的判斷才可以。但是利用棧以及一些演算法就能輕鬆實現計算的功能。我們下面的例子也將會利用棧結構來實現簡易的計算器的功能。
三、入棧和出棧
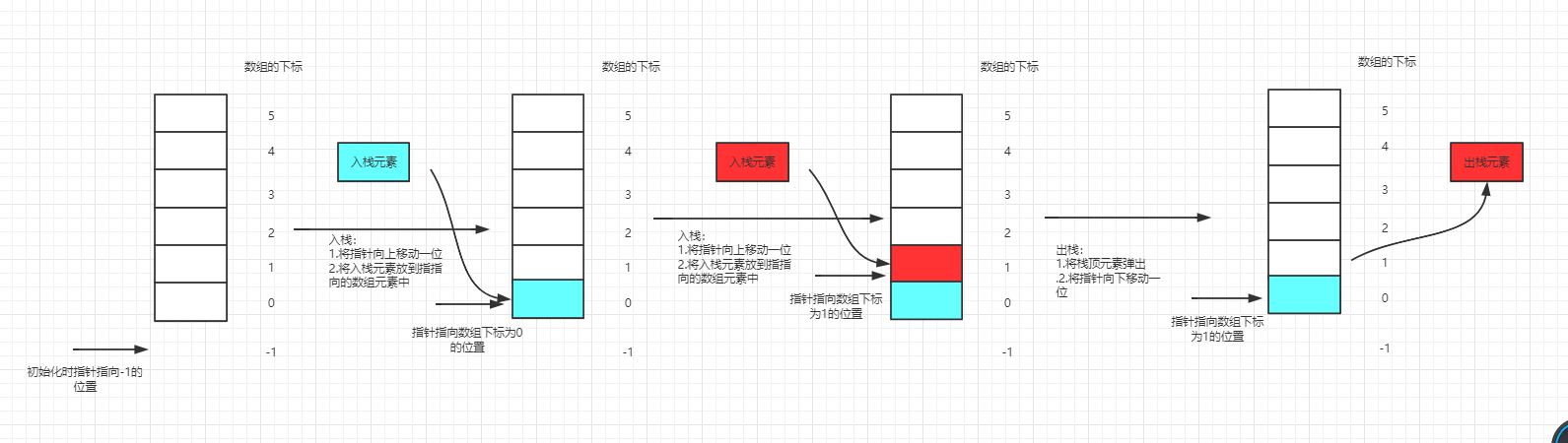
棧結構可以使用數組結構和鏈表結構來實現,因此不同的實現方式,入棧和出棧的實現方式也會有所區別。基於數組實現的棧的入棧和出棧操作實質是在內部維護了一個指針,這個指針指向的元素即為棧頂元素,入棧時講指針向上移動一位,相反地則向下移動一位。基於鏈表的棧就沒有了指針的概念。鏈表使用單向鏈表即可實現。鏈表的出棧和入棧實質上維護的鏈表頭部元素。下面使用示意圖來簡單的演示一下兩種結構的入棧和出棧的流程:
1、基於數組的入棧和出棧:
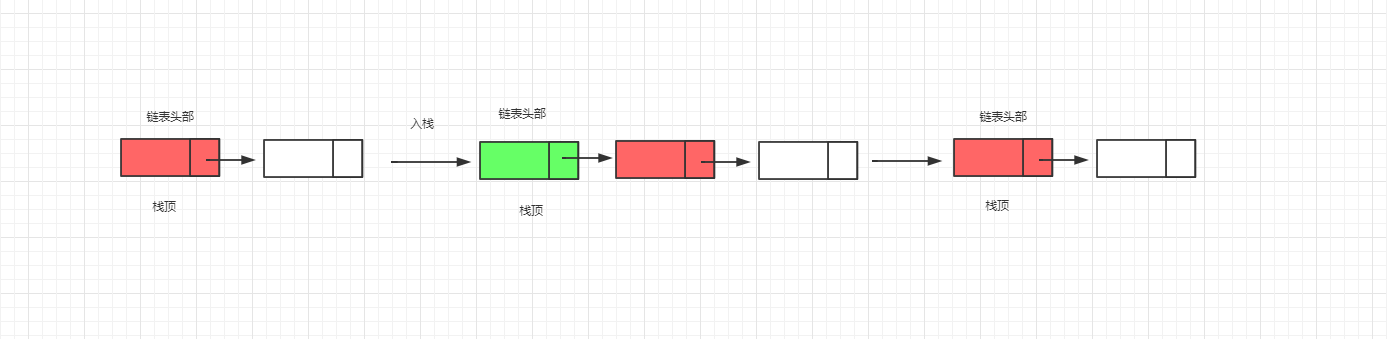
2.鏈表的入棧和出棧
四、程式碼實現
1.數組
/**
* 基於數組實現的棧
*/
public class ArrayStack<E> implements Stack<E> {
private Object[] data;
private int index = -1;
private int deep;
private static final int DEFAULT_CAPACITY = 1 << 4;
public ArrayStack() {
deep = DEFAULT_CAPACITY;
data = new Object[deep];
}
public ArrayStack(int capacity) {
if (capacity <= 0) {
capacity = DEFAULT_CAPACITY;
}
deep = capacity;
data = new Object[deep];
}
/**
* 添加數據,數組滿了就不添加
* @param e 入棧元素
* @return
*/
@Override
public E push(E e) {
if (isFull()) {
System.out.println("棧已滿");
return null;
}
data[++index] = e;
return e;
}
/**
* 彈出元素
* @return 棧頂元素
*/
@Override
public E pop() {
if (isEmpty()) {
System.out.println("棧為空");
return null;
}
return (E) data[index--];
}
/**
* 查看棧頂元素
* @return
*/
@Override
public E peek() {
if (isEmpty()) {
System.out.println("棧為空");
return null;
}
return (E) data[index];
}
/**
* 棧深度
* @return
*/
@Override
public int size() {
return index + 1;
}
private boolean isEmpty() {
return index <= -1;
}
private boolean isFull() {
return deep == index + 1;
}
2.鏈表
/**
* 基於鏈表實現的棧
* @param <E>
*/
public class LinkStack<E> implements Stack<E> {
private Node<E> head;
private int size;
@Override
public E push(E e) {
Node<E> node = new Node<>(e);
if (head == null) {
head = node;
}else {
Node<E> n = head;
head = node;
head.next = n;
}
size++;
return e;
}
@Override
public E pop() {
if (head == null) {
return null;
}
E data = head.data;
head = head.next;
size--;
return data;
}
@Override
public E peek() {
return head == null ? null : head.data;
}
@Override
public int size() {
return size;
}
private static class Node<E> {
E data;
Node<E> next;
public Node(E e) {
data = e;
}
}
}
/**
* 棧結構
*/
public interface Stack<E> {
/**
* 入棧
* @param e 入棧元素
* @return 入棧元素
*/
E push(E e);
/**
* 將棧頂元素彈出
* @return 棧頂元素
*/
E pop();
/**
* 查看棧頂元素,該方法不會彈出棧頂元素
* @return 棧頂元素
*/
E peek();
/**
* 查看棧深度
* @return 棧深度
*/
int size();
}
五、應用實例:簡易計算器
在進入寫程式碼之前需要知道的前置知識是:前綴表達式(也叫波蘭表達式),中綴表達式和後綴表達式(也叫逆波蘭表達式)。
前綴、中綴、後綴表達式是對表達式的不同記法,其區別在於運算符相對於操作數的位置不同,前綴表達式的運算符位於操作數之前,中綴和後綴同理
舉例:
中綴表達式:1 + (2 + 3) × 4 – 5
前綴表達式:- + 1 × + 2 3 4 5
後綴表達式:1 2 3 + 4 × + 5 –
中綴表達式 中綴表達式是一種通用的算術或邏輯公式表示方法,操作符以中綴形式處於操作數的中間。中綴表達式是人們常用的算術表示方法。 雖然人的大腦很容易理解與分析中綴表達式,但對電腦來說中綴表達式卻是很複雜的,因此計算表達式的值時,通常需要先將中綴表達式轉換為前綴或後綴表達式,然後再進行求值。對電腦來說,計算前綴或後綴表達式的值非常簡單。
我下面講解的例子中是利用後綴表達式的演算法來實現的,因此,程式碼中回涉及到 運算字元串轉中綴表達式,中綴表達式轉後綴表達式的過程。
後綴表達式步驟
從左至右掃描表達式,遇到數字時,將數字壓入堆棧,遇到運算符時,彈出棧頂的兩個數,用運算符對它們做相應的計算(次頂元素 和 棧頂元素),並將結果入棧;重複上述過程直到表達式最右端,最後運算得出的值即為表達式的結果。
例如: (3+4)×5-6 對應的後綴表達式就是 3 4 + 5 × 6 – , 針對後綴表達式求值步驟如下:
1.從左至右掃描,將3和4壓入堆棧;
2.遇到+運算符,因此彈出4和3(4為棧頂元素,3為次頂元素),計算出3+4的值,得7,再將7入棧;
3.將5入棧;
4.接下來是×運算符,因此彈出5和7,計算出7×5=35,將35入棧;
5.將6入棧;
6.最後是-運算符,計算出35-6的值,即29,由此得出最終結果
根據上面的步驟,我們可以使用程式碼來實現:
/**
* 根據後綴表達式計算值
* @param items 後綴表達式
* @return 計算結果
*/
public int calculate(List<String> items) {
/**
* 用於保存過程變數和操作符等
*/
Stack<String> stack = new LinkStack<>();
//便利
for (String item : items) {
//如果為數字,直接放入棧中
if (item.matches("\\d+")) {
stack.push(item);
}else {
//彈出棧頂元素進行運算
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res;
switch (item) {
case "+" :
res = num1 + num2;
break;
case "-" :
res = num1 - num2;
break;
case "*" :
res = num1 * num2;
break;
case "/" :
res = num1 / num2;
break;
default:
throw new RuntimeException("非法的運算符:" + item);
}
//運算完將結果壓入棧中
stack.push("" + res);
}
}
//整個表達式掃描結束後,此時棧中只剩一個元素,該元素即為結算結果,從棧中彈出即可
return Integer.parseInt(stack.pop());
}
測試結果:
public static void main(String[] args) {
Calculator calculator = new Calculator();
List<String> items = new ArrayList<>();
items.add("3");
items.add("4");
items.add("+");
items.add("5");
items.add("*");
items.add("6");
items.add("-");
System.out.println(calculator.calculate(items));
}
//結果:29
雖然後面可以計算出表達式的最終結果,但是的實際的應用中計算的表達式往往都是按照我們的計算習慣來書寫的(即中綴表達式,如(3+4)×5-6)。因此,想要正確的得到結果我們需要再多一個步驟,就是人們習慣的計算方式的中綴表達式轉換成對電腦友好的後綴表達式。具體步驟如下:
1)初始化兩個棧:運算符棧s1和儲存中間結果的棧s2;
2)從左至右掃描中綴表達式;
3)遇到操作數時,將其壓s2;
4)遇到運算符時,比較其與s1棧頂運算符的優先順序:
4.1)如果s1為空,或棧頂運算符為左括弧「(」,則直接將此運算符入棧;
4.2)否則,若優先順序比棧頂運算符的高,也將運算符壓入s1;
4.3)否則,將s1棧頂的運算符彈出並壓入到s2中,再次轉到(4-1)與s1中新的棧頂運算符相比較;
5)遇到括弧時:
5.1) 如果是左括弧「(」,則直接壓入s1
5.2) 如果是右括弧「)」,則依次彈出s1棧頂的運算符,並壓入s2,直到遇到左括弧為止,此時將這一對括弧丟棄
6)重複步驟2至5,直到表達式的最右邊
7)將s1中剩餘的運算符依次彈出並壓入s2
8)依次彈出s2中的元素並輸出,結果的逆序即為中綴表達式對應的後綴表達式
具體程式碼如下:
(一)、解析算式
/**
* 將表達式解析成List
* @param expression 表達式
* @return
*/
private List<String> parseExpr(String expression) {
char[] chars = expression.toCharArray();
int len = chars.length;
List<String> items = new ArrayList<>(len);
int index = 0;
while (index < len) {
char c = chars[index];
//數字
if (c >= 48 && c <= 57) {
String tmp = "";
//操作數大於一位數,主要是通過判斷下一位是否為數字
while (index < chars.length && chars[index] >= 48 && chars[index] <= 57) {
tmp += chars[index];
index++;
}
items.add(tmp);
}else {
items.add(c + "");
index++;
}
}
return items;
}
(二)、獲取運算符的優先順序
/**
* 獲取運算符的優先順序,數字越大優先順序越大
* @param operateChar 運算符
* @return 優先順序
*/
private int priority(String operateChar) {
if ("*".equals(operateChar) || "/".equals(operateChar)) {
return 2;
}else if ("+".equals(operateChar) || "-".equals(operateChar)) {
return 1;
}else {
//throw new RuntimeException("非法的操作符:" + operateChar);
return 0;
}
}
(三)、中綴轉後綴表達式
/**
* 1)初始化兩個棧:運算符棧operateStack和儲存中間結果的棧tmp;
* 2)從左至右掃描中綴表達式;
* 3)遇到操作數時,將其壓tmp;
* 4)遇到運算符時,比較其與operateStack棧頂運算符的優先順序:
* 4.1)如果operateStack為空,或棧頂運算符為左括弧「(」,則直接將此運算符入棧;
* 4.2)否則,若優先順序比棧頂運算符的高,也將運算符壓入operateStack;
* 4.3)否則,將operateStack棧頂的運算符彈出並壓入到tmp中,再次轉到(4-1)與operateStack中新的棧頂運算符相比較;
* 5)遇到括弧時:
* 5.1) 如果是左括弧「(」,則直接壓入operateStack
* 5.2) 如果是右括弧「)」,則依次彈出operateStack棧頂的運算符,並壓入tmp,直到遇到左括弧為止,此時將這一對括弧丟棄
* 6)重複步驟2至5,直到表達式的最右邊
* 7)將operateStack中剩餘的運算符依次彈出並壓入tmp
* 8)依次彈出tmp中的元素並輸出,結果的逆序即為中綴表達式對應的後綴表達式
* @param expr 中綴表達式
* @return 後綴表達式
*/
public List<String> midfixToSuffix(String expr) {
/**
* 將表達式的操作數和運算符轉換成集合
*/
List<String> items = parseExpr(expr);
//操作數棧
Stack<String> operateStack = new LinkStack<>();
//臨時變數的保存集合,這裡使用了List集合
//如果用棧也可以實現,但是需要在最後將彈出棧元素的逆序進行運算
//所以使用List集合避免了這個轉換的問題
List<String> tmp = new ArrayList<>();
//操作的位置
int index = 0;
//表達式長度
int len = items.size();
while (index < len) {
String item = items.get(index);
//遇到操作數時,將其壓tmp;
if (item.matches("\\d+")) {
tmp.add(item);
}else if (item.equals("(")) {//如果是左括弧「(」,則直接壓入operateStack
operateStack.push(item);
} else if (item.equals(")")) {//如果是右括弧「)」,則依次彈出operateStack棧頂的運算符,並壓入tmp,直到遇到左括弧為止,此時將這一對括弧丟棄
while (!operateStack.peek().equals("(")) {
tmp.add(operateStack.pop());
}
//直接彈出棧頂元素即可
operateStack.pop();
} else {//遇到運算符時,比較其與operateStack棧頂運算符的優先順序
//如果operateStack為空,或棧頂運算符為左括弧「(」,則直接將此運算符入棧;
if (operateStack.isEmpty() || "(".equals(operateStack.peek())) {
operateStack.push(item);
}else if (priority(item) > priority(operateStack.peek())) {//否則,若優先順序比棧頂運算符的高,也將運算符壓入operateStack;
tmp.add(item);
} else {//否則,將operateStack棧頂的運算符彈出並壓入到tmp中,再次轉到(4-1)與operateStack中新的棧頂運算符相比較;
while (!operateStack.isEmpty() && priority(item) <= priority(operateStack.peek())) {
tmp.add(operateStack.pop());
}
//將運算符壓入棧
operateStack.push(item);
}
}
//沒一輪結束需要將操作位置往後移動一位
index++;
}
//解析結束後需要將剩下的棧元素全部彈出來放入到tmp中
while (!operateStack.isEmpty()) {
tmp.add(operateStack.pop());
}
return tmp;
}
(四)、計算結果
/**
* 根據後綴表達式計算值
* @param items 後綴表達式
* @return 計算結果
*/
public int calculate(List<String> items) {
/**
* 用於保存過程變數和操作符等
*/
Stack<String> stack = new LinkStack<>();
//便利
for (String item : items) {
//如果為數字,直接放入棧中
if (item.matches("\\d+")) {
stack.push(item);
}else {
//彈出棧頂元素進行運算
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res;
switch (item) {
case "+" :
res = num1 + num2;
break;
case "-" :
res = num1 - num2;
break;
case "*" :
res = num1 * num2;
break;
case "/" :
res = num1 / num2;
break;
default:
throw new RuntimeException("非法的運算符:" + item);
}
//運算完將結果壓入棧中
stack.push("" + res);
}
}
//整個表達式掃描結束後,此時棧中只剩一個元素,該元素即為結算結果,從棧中彈出即可
return Integer.parseInt(stack.pop());
}
(五)、測試
public static void main(String[] args) {
Calculator calculator = new Calculator();
List<String> items = calculator.midfixToSuffix("(3+4)*5-6");
System.out.println("後綴表達式為:" + items);
int result = calculator.calculate(items);
System.out.println("運算結果為: " + result);
}
//後綴表達式為:[3, 4, +, 5, *, 6, -]
//運算結果為: 29
完整的程式碼如下:
public class Calculator {
public static void main(String[] args) {
Calculator calculator = new Calculator();
List<String> items = calculator.midfixToSuffix("(3+4)*5-6");
System.out.println("後綴表達式為:" + items);
int result = calculator.calculate(items);
System.out.println("運算結果為: " + result);
}
/**
* 1)初始化兩個棧:運算符棧operateStack和儲存中間結果的棧tmp;
* 2)從左至右掃描中綴表達式;
* 3)遇到操作數時,將其壓tmp;
* 4)遇到運算符時,比較其與operateStack棧頂運算符的優先順序:
* 4.1)如果operateStack為空,或棧頂運算符為左括弧「(」,則直接將此運算符入棧;
* 4.2)否則,若優先順序比棧頂運算符的高,也將運算符壓入operateStack;
* 4.3)否則,將operateStack棧頂的運算符彈出並壓入到tmp中,再次轉到(4-1)與operateStack中新的棧頂運算符相比較;
* 5)遇到括弧時:
* 5.1) 如果是左括弧「(」,則直接壓入operateStack
* 5.2) 如果是右括弧「)」,則依次彈出operateStack棧頂的運算符,並壓入tmp,直到遇到左括弧為止,此時將這一對括弧丟棄
* 6)重複步驟2至5,直到表達式的最右邊
* 7)將operateStack中剩餘的運算符依次彈出並壓入tmp
* 8)依次彈出tmp中的元素並輸出,結果的逆序即為中綴表達式對應的後綴表達式
* @param expr 中綴表達式
* @return 後綴表達式
*/
public List<String> midfixToSuffix(String expr) {
/**
* 將表達式的操作數和運算符轉換成集合
*/
List<String> items = parseExpr(expr);
//操作數棧
Stack<String> operateStack = new LinkStack<>();
//臨時變數的保存集合,這裡使用了List集合
//如果用棧也可以實現,但是需要在最後將彈出棧元素的逆序進行運算
//所以使用List集合避免了這個轉換的問題
List<String> tmp = new ArrayList<>();
//操作的位置
int index = 0;
//表達式長度
int len = items.size();
while (index < len) {
String item = items.get(index);
//遇到操作數時,將其壓tmp;
if (item.matches("\\d+")) {
tmp.add(item);
}else if (item.equals("(")) {//如果是左括弧「(」,則直接壓入operateStack
operateStack.push(item);
} else if (item.equals(")")) {//如果是右括弧「)」,則依次彈出operateStack棧頂的運算符,並壓入tmp,直到遇到左括弧為止,此時將這一對括弧丟棄
while (!operateStack.peek().equals("(")) {
tmp.add(operateStack.pop());
}
//直接彈出棧頂元素即可
operateStack.pop();
} else {//遇到運算符時,比較其與operateStack棧頂運算符的優先順序
//如果operateStack為空,或棧頂運算符為左括弧「(」,則直接將此運算符入棧;
if (operateStack.isEmpty() || "(".equals(operateStack.peek())) {
operateStack.push(item);
}else if (priority(item) > priority(operateStack.peek())) {//否則,若優先順序比棧頂運算符的高,也將運算符壓入operateStack;
tmp.add(item);
} else {//否則,將operateStack棧頂的運算符彈出並壓入到tmp中,再次轉到(4-1)與operateStack中新的棧頂運算符相比較;
while (!operateStack.isEmpty() && priority(item) <= priority(operateStack.peek())) {
tmp.add(operateStack.pop());
}
//將運算符壓入棧
operateStack.push(item);
}
}
//沒一輪結束需要將操作位置往後移動一位
index++;
}
//解析結束後需要將剩下的棧元素全部彈出來放入到tmp中
while (!operateStack.isEmpty()) {
tmp.add(operateStack.pop());
}
return tmp;
}
/**
* 獲取運算符的優先順序,數字越大優先順序越大
* @param operateChar 運算符
* @return 優先順序
*/
private int priority(String operateChar) {
if ("*".equals(operateChar) || "/".equals(operateChar)) {
return 2;
}else if ("+".equals(operateChar) || "-".equals(operateChar)) {
return 1;
}else {
//throw new RuntimeException("非法的操作符:" + operateChar);
return 0;
}
}
/**
* 將表達式解析成List
* @param expression 表達式
* @return
*/
private List<String> parseExpr(String expression) {
char[] chars = expression.toCharArray();
int len = chars.length;
List<String> items = new ArrayList<>(len);
int index = 0;
while (index < len) {
char c = chars[index];
//數字
if (c >= 48 && c <= 57) {
String tmp = "";
//操作數大於一位數,主要是通過判斷下一位是否為數字
while (index < chars.length && chars[index] >= 48 && chars[index] <= 57) {
tmp += chars[index];
index++;
}
items.add(tmp);
}else {
items.add(c + "");
index++;
}
}
return items;
}
/**
* 根據後綴表達式計算值
* @param items 後綴表達式
* @return 計算結果
*/
public int calculate(List<String> items) {
/**
* 用於保存過程變數和操作符等
*/
Stack<String> stack = new LinkStack<>();
//便利
for (String item : items) {
//如果為數字,直接放入棧中
if (item.matches("\\d+")) {
stack.push(item);
}else {
//彈出棧頂元素進行運算
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res;
switch (item) {
case "+" :
res = num1 + num2;
break;
case "-" :
res = num1 - num2;
break;
case "*" :
res = num1 * num2;
break;
case "/" :
res = num1 / num2;
break;
default:
throw new RuntimeException("非法的運算符:" + item);
}
//運算完將結果壓入棧中
stack.push("" + res);
}
}
//整個表達式掃描結束後,此時棧中只剩一個元素,該元素即為結算結果,從棧中彈出即可
return Integer.parseInt(stack.pop());
}
}
簡單的計算器基本已經寫完了。如果你感興趣的話,可以將上面的程式碼拿下來自己顯現更多的功能,比如說支援小數,其他的運算,表達式中允許有空格等。這些功能實現起來是不難的,只要在上面的基礎上做一些改動即可。


