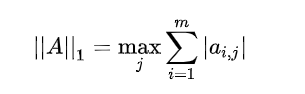範數的理解。
有關於範數的理解。
範數理解(0範數,1範數,2範數)
我們可以這樣理解,一個集合(向量),通過一種映射關係(矩陣),得到另外一個集合(另外一個向量)。 **範數的本質是距離,存在的意義是實現比較。因為向量與矩陣無法像標量直接比較大小,因而通過範數(稱為函數或者映射也可以)把不能比較的量轉換為可以比較的實數。**
簡單說:0範數表示向量中非零元素的個數(即為其稀疏度)。
1範數表示為,絕對值之和。
2範數則指模。
向量範數: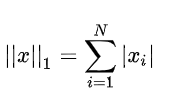
1-範數 ,即集合元素向量的絕對值之和。 2-範數,歐幾里得範數,常用計算向量長度,即向量元素絕對值的平方和再開方,∞範數,即所有向量元素絕對值中的最大值。負無窮範數,即所有向量元素絕對值中的最小值。p範數,即向量元素絕對值的p次方和的1/p次冪。
矩陣範數: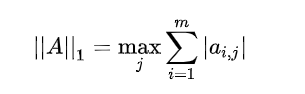
1-範數:列和範數,即所有矩陣列向量絕對值之和的最大值。
2-範數:譜範數,矩陣ATAA的最大特徵值開平方根。
無窮範數:行和範數,即所有矩陣行向量絕對值之和的最大值。
F-範數:即矩陣元素絕對值的平方和再開平方
矩陣的核範數:矩陣的奇異值(將矩陣svd分解)之和。
矩陣的L0範數:矩陣的非0元素的個數,通常用它來表示稀疏,L0範數越小0元素越多,也就越稀疏.
矩陣的L1範數:矩陣中的每個元素絕對值之和,它是L0範數的最優凸近似,因此它也可以表示稀疏
矩陣的L2範數:就是F範數。
矩陣的L21範數:矩陣先以每一列為單位,求每一列的F範數(也可認為是向量的2範數),然後再將得到的結果求L1範數(也可認為是向量的1範數),很容易看出它是介於L1和L2之間的一種範數。