演算法與數據結構（4）：堆排序

堆排序（HeapSort）是最常用的排序演算法之一。這種排序演算法同時具有插入排序和歸併排序的優點。與插入排序一樣，具有空間原址性，即任何時候都只需要常數個額外的空間儲存臨時數據（對此，請大家回想一下歸併排序，隨著問題規模的越大，需要的額外空間就越大，在解決大型問題時，這是不可接受的缺點）。與歸併排序一樣，具有 \(O(n*lgn)\) 的時間複雜度。

其實一句話總結，堆排序具有 \(O(1)\) 的空間複雜度，具有 \(O(n*lgn)\) 的時間複雜度。

同時，在這裡需要強調一點，此文所說的堆是一種數據結構，其類似於我們上一篇文章所說的樹，在一些高級語言中，例如 Java 中，「堆」是一種「垃圾收集存儲機制」，這僅僅是因為 Java 的「垃圾收集存儲機制」最早的數據結構採用的是「堆」。因為這個系列是介紹演算法與數據結構的，所以此系列後續提到的所有「堆」，都是只一種數據結構，希望讀者在自行了解相關知識時，注意區分。

此文堆排序的完整程式碼可以在我的github上查看。

堆

如下圖所示，（二叉）堆可以被理解為一個完全二叉樹：

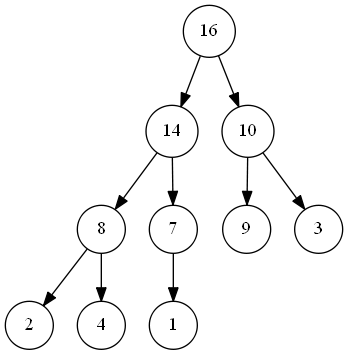
通常情況下，我們採用數組來存儲（雖然我們也可以採用上一篇文章中提到的樹來實現，但這必然會帶來額外的複雜度。雖然我們採用數組實現，但在理解時請將其視為樹，查看注釋）。

除了最底層外，該樹是完全充滿的，而且最底層是從左往右依次填充。表示堆的數組應該包括兩個屬性，heap_length 和 heap_size ，其中 heap_length 表示數組總長度，heap_size 表示有效數據個數，同時滿足 \(0 \leq heap\_size \leq length\) 。為了方便寫程式碼，我們如下定義：

#define HEAP_LENGTH 20 // 數組長度

int array_to_sort[HEAP_LENGTH + 1] = {HEAP_LENGTH, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
                                      20, 19, 18, 17, 16, 15, 14, 13, 12, 11};

我們將 array_to_sort[0] 解釋為 heap_size，故 array_to_sort 的實際長度應為 heap_length + 1。這樣做的目的其實是為了下文方便，給定一個節點下標 i ，那麼他的父節點，左孩子和右孩子節點下標分別為：

#define PARENT(i) (i / 2)
#define LEFT(i) (2 * i)
#define RIGHT(i) (2 * i + 1)

對於大多數的電腦而言，通過將 i 的值算數左移一位，即可在一條指令內計算出 2i，將 i 的值算數右移一位，即可在一條指令內計算出 \(\lfloor \frac{i}{2} \rfloor\) ，不過在現代編譯器中，編譯器會自動將乘2與除2運算自動優化為移位操作，所以我們在寫程式碼時如果需要乘除法，盡量只進行乘2與除2操作即可。

二叉堆可以分為兩種形式：最大堆和最小堆。最小堆是指除了根節點以外的其他所有節點 i 都需要滿足：

\[A[PARENT(i)] \leq A[i]
\]

即某個節點的值至多與其父節點一樣小，因此堆中的最小元素存放在根節點中，並且此樹的任意子樹中，該子樹的中的所有元素的最小值也在子樹的根節點。最大堆與此正好相反，是指除了根節點以外的所有節點 i 都有：

\[A[PARENT(i)] \geq A[i]
\]

此文中採用的堆排序使用最大堆。

如果我們把堆看成一棵樹，則堆中某個節點的高度為該節點到葉節點的最長簡單路徑上的邊的數量，而堆的高度為根節點的高度。

下文的程式碼中，會涉及到swap函數，我們先將此函數的程式碼展示一下：

// 交換數組array的 下標i 和 下標j 對應的值
int swap(int *array, int i, int j){
    int temp;
    temp = array[i];
    array[i] = array[j];
    array[j] = temp;
    return 0;
}

維護堆

首先展示一下程式碼：

// 遞歸維護最大堆
int MaintainMaxHeap(int *heap, int i){
    int largest;
    int left = LEFT(i);
    int right = RIGHT(i);
    if(left <= heap[0] && heap[left] > heap[i]){
        largest = left;
    } else{
        largest = i;
    }
    if(right <= heap[0] && heap[right] > heap[largest]){
        largest = right;
    }
    if(largest != i){
        swap(heap, largest, i);
        MaintainMaxHeap(heap, largest);
    }
    return 0;
}

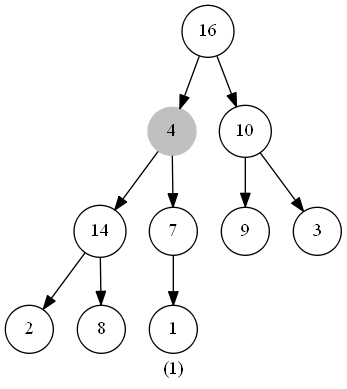
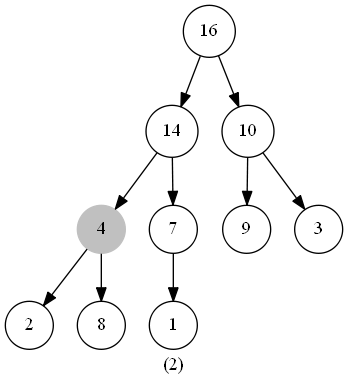
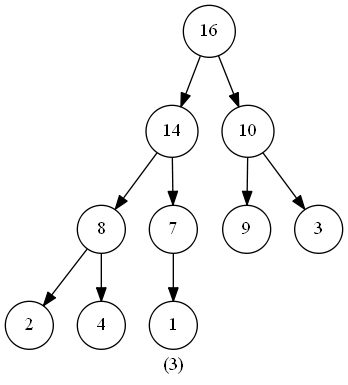
此函數的作用是維護最大堆的性質。函數的輸入為一個堆（數組）heap，一個下標 i 。調用前，調用者需要保證根節點為 LEAT(i) 和 RIGHT(i) 的二叉樹都是最大堆（具體保證方法下文會闡述），此時我們需要將以下標 i 為根節點的子樹修改為最大堆（因為heap[i] 可能小於 heap[LEFT(i)] 或 heap[RIGHT(i)] ）。

在程式碼中，我們從 heap[i] 和 heap[LEFT(i)] 、heap[RIGHT(i)] 中選出值最大的數，將其下標儲存在 largest 中。若heap[i] 就是最大值，說明此堆已經符合最大堆的特性，無需進行其他操作；反之則將 heap[i] 與 heap[largest] 交換，交換後，下標為largest的節點是原來的 heap[i]，以此節點為根節點的子樹有可能也會違反最大堆的特性，那麼我們此時只需再對此節點調用一次 MaintainMaxHeap() 函數，如此遞歸下去，完成堆的維護。

時間複雜度

對於一棵以 i 為根節點，大小為 n 的子樹，MaintainMaxHeap() 的時間消耗分為兩部分：調整 heap[i]，heap[LEFT(i)]，heap[RIGHT(i)] ，代價為 \(\Theta(1)\) ；若進行了交換，維護 i 節點的一個子樹的時間（時間複雜度一般指最壞情況，所以我們需要假定遞歸調用會發生）。而每一個孩子的子樹大小至多為 \(\frac{2n}{3}\) （取最壞情況，樹的底層正好半滿，即左子樹的深度正好比右子樹大1，且左子樹是一個完全二叉樹），那麼，運行一次 MaintainMaxHeap() 的時間消耗為：

\[T(n) \leq T(\frac{2n}{3}) + \Theta(1)
\]

由主定理可得，上述遞歸式的解為 \(T(n)=O(lgn)\) 。

建堆

上文我們提到，在維護堆的性質時，需要保證左右子樹均為最大堆，那麼最為簡單的方法就是讓整個堆都變成最大堆，這樣，如果替換了一個數，他的左右子樹必能保證為一個最大堆。

對此，我們採用自底向上的方法，把一個大小為 n 的數組轉換為最大堆。

// 建堆
int BuildHeap(int *heap){
    int i;
    for(i = PARENT(heap[0]); i >= 1; i--){
        MaintainMaxHeap(heap, i);
    }
    return 0;
}

正確性分析

初始化：在第一次循環以前，\(i=\lfloor \frac{n}{2} \rfloor\) ，而 \(\lfloor \frac{n + 1}{2} \rfloor\) ， \(\lfloor \frac{n + 2}{2} \rfloor\) ，… ，\(n\) 都是葉節點，故下標大於 i 的節點都是一個最大堆的根節點。

保持：因為節點 i 的孩子節點下標均大於 i ，故以節點 i 的子節點為根節點的樹都是一個最大堆，所以我們可以對節點 i 調用 MaintainMaxHeap() 函數，調用完成後，以節點 i 為根節點的樹是一個最大堆，其他下標大於 i 的節點要麼不受影響，要麼在 MaintainMaxHeap() 函數中，依然保持了最大堆的性質。一次循環結束，i 自減，此時下標大於 i 的節點都是一個最大堆的根節點。

終止：循環結束時，i==0，那麼此時下標大於 0 的節點都是一個最大堆的根節點，即整個樹已經成為了一個最大堆（heap[0]中儲存的是 heap_size，不是堆中的元素，希望各位讀者不要忘記了）。

時間複雜度

對於這個過程，我們可以進行簡單的估算。每次調用 MaintainMaxHeap() 函數，其時間複雜度不超過 \(O(lgn)\) ，MaintainMaxHeap() 函數一共被調用 \(O(n)\) 次，那麼其時間複雜度不超過 \(O(n*lgn)\) 。這個上界雖然正確，但不夠精確。我們下面來進行一下進一步的分析（如果讀者的數學水平有限的話，可以暫時跳過下面的具體分析）。

首先，對於一個含 \(n\) 個元素的堆，其高度為 \(\lfloor lgn \rfloor\) ，其中高度為 \(h\) 的節點，最多有 \(\lceil \frac{n}{2^{h+1}} \rceil\) 個（請各位讀者再仔細看一下上文的關於堆的高度的概念，之前教朋友的時候，很多人是把概念都弄錯了，從而覺得是我這個地方算錯了2333）

在一個高度為 \(h\) 的節點上運行 MaintainMaxHeap() 的時間複雜度是 \(O(h)\) ，那麼 BuildHeap() 的總的時間複雜度為

\[\sum_{h=0}^{\lfloor lgn \rfloor} {\lceil \frac{n}{2^{h+1}} \rceil}O(h) = O(n \sum_{h=0}^{\lfloor lgn \rfloor} {\frac{h}{2^h}} )
\]

使用無窮級數或者數列的知識，我們可以得到：

\[\sum_{h=0}^{ \infty } {\frac{h}{2^h}} = \frac{1/2}{(1-1/2)^2} = 2
\]

那麼最終的時間複雜度為：

\[O(n \sum_{h=0}^{\lfloor lgn \rfloor} {\frac{h}{2^h}} ) = O(n \sum_{h=0}^{ \infty } {\frac{h}{2^h}}) = O(2n) = O(n)
\]

沒想到吧，我們居然可以在線性時間內，把一個無序數組構造為一個最大堆。

堆排序

前面鋪墊了這麼多，終於進入正題了，如何進行堆排序？

// 堆排序
int HeapSort(int *heap){
    int i;
    BuildHeap(heap);
    for(i = heap[0]; i >= 1; i--){
        swap(heap, 1, heap[0]);
        heap[0] -= 1;
        MaintainMaxHeap(heap, 1);
    }
}

步驟非常簡單，首先建立一個最大堆，那麼此時數組中的最大元素就在根節點 heap[1] ，此時我們將其與 heap[heap_size] 交換，我們即可將此元素放在正確的位置（最終的排序效果為遞增），此時我們將 heap_size 減一，將剛才被選出的最大值從堆中去掉。對於此時的堆，根節點的兩個子樹依然保持著最大堆的特性，但根節點可能會違背最大堆的特性，此時我們調用 MaintainMaxHeap(heap, 1) 即可將其重新轉換為一個最大堆，重複此操作，直到將所有節點均從堆中去掉，那麼整個數組也就排序完成了。

時間複雜度

堆排序的第一步是建立一個最大堆，其時間複雜度我們已經在上文分析了，為 \(O(n)\) 。

調用 n 次 MaintainMaxHeap()，每次的時間複雜度為 \(O(lgn)\) 。

那麼總的時間複雜度為 \(O(n*lgn)\) 。

不過此時可能就會有好奇的讀者問了，在建堆的過程中，需要調用 \(n\) 次，每次複雜度不超過 \(O(lgn)\) ，這不是和堆排序是一樣的嗎？為什麼建堆最後算出來時間複雜度是 \(O(n)\) ，而堆排序就是 \(O(n*lgn)\) 呢？是的，關於堆排序的時間複雜度的計算我只是給了一個感性的估計方法，如果想要非常精確的計算出來的話，也是需要像建堆時那樣一步一步計算的，只是計算出來的結果也依然是 \(O(n*lgn)\) ，所以為了偷懶，我就不驗算了嘛，畢竟還是挺費時的。

注釋

前文我們提到對於堆這種數據結構，雖然我們採用數組實現，但在理解時請將其視為樹，其實在電腦中，所有的內容都是 0-1 串，無論你是儲存了一張圖片，還是一個word文檔，他們都是 0-1 串，但為什麼會有不同的呈現方式呢？其實就是對其的解釋不同。例如在 Windows 作業系統下，文件具有一個屬性叫做後綴名，當你修改了其後綴名以後，文件內容其實什麼都沒有變化，唯一的變化是對其解釋不同了。例如對於一個 html 文件，當你把他解釋為一個網頁時，可以使用瀏覽器打開，效果就是我們平時所看到的各種網頁，當你把他解釋為一個文本文件時，就可以使用記事本或者其他編輯器打開，你就能查看他的源程式碼。Windows 採用後綴名的方式，一是為了方便自動選擇合適的軟體打開某個文件（當然，你是可以在每次打開時手動選擇的，但每次都手動選擇，是真的不適合我這種懶人），二是方便用戶了解文件內容，比如當用戶看到一個後綴名為 png 的文件時，就能知道這大概率是圖片（畢竟不能排除有人故意亂改後綴名），後綴名是 zip 時，能知道這是一個壓縮包。而在 Linux 下，系統選擇打開某個文件的軟體時，只查看文件開頭的一部分字元串（不同的文件格式具有不同的文件頭，或者被稱為魔數），據此來判斷文件格式，而後綴名的作用就只有我們上文所說的第二個作用了。

結語

本文我們詳細介紹了堆排序的相關內容，如果前面幾篇文章認真看了的話，理解起來也並不困難，如果只是想要知道堆排序怎麼寫的話，似乎前面幾篇文章頁不需要看2333，畢竟主要難度還是在於時間複雜度的計算上。但如果想要深入理解演算法這個巨坑的話，建議打好數學基礎，在時間複雜度的計算上，數學基礎是很重要的。下一篇文章我們將會介紹快速排序。

原文鏈接：albertcode.info

個人部落格：albertcode.info

Tags: 堆排序數據結構演算法演算法與數據結構