0基础学算法 第四弹 高精度
- 2020 年 3 月 18 日
- 笔记
今天写这个的时候心情是非常糟糕的，因为我写了这篇博文四遍，每次都因为网页问题，不是需要刷新就是要重开，以至于我昨天一天和今天上午写了整整4遍没提交成功，不唠嗑了，切入正题。
高精度是一种计算大数的算法，通常我们计算的时候会用int，要是范围大了就会用long long类型，这有张表，共大家参考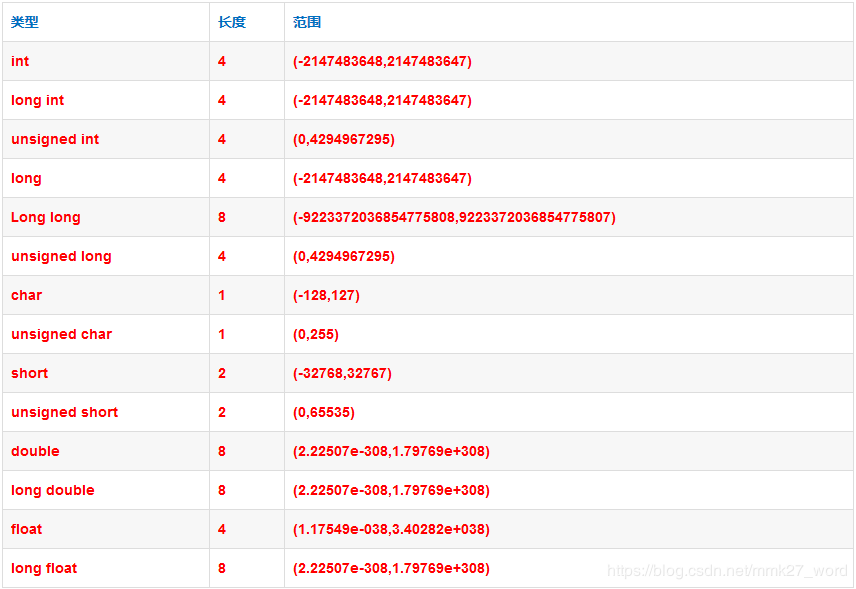
一旦数据超过了long long型，就会用到了高精度，高精度的基本原理是将数字分别存入数组的每一项中，然后将它模拟竖式计算，刚好他满足竖式计算的条件，只要小心进退位的问题就好了
由于洛谷上有模版题，所以今天我们就结合题目一起来理解高精度
高精度的加减法
P1601 https://www.luogu.com.cn/problem/P1601
P1601是高精度的加法，先思考一下，不要看题解，如果你有思路，就去实现一下吧，没有思路也没事，不管怎样，你都可以继续看这篇博客。
好，请确保你已经思考过了，如果你看过我的第一弹的流程图，就把你的思路画下来，然后就把它实现好了。
大致思路
如果你完成了前面的内容，那么恭喜你，你离成功只有一步了，首先看看流程图，梳理一下思路，再照着流程图完成代码吧
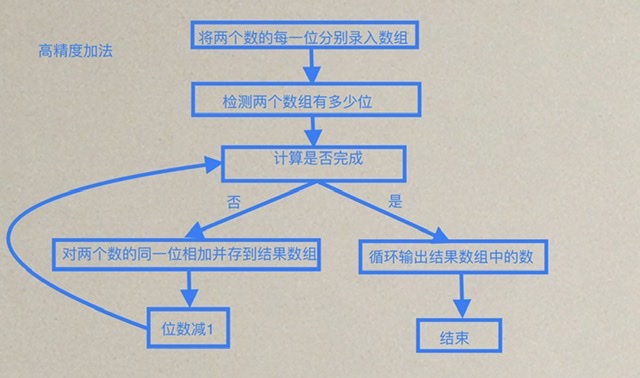思路就是这样了，那我们可以根据流程图，去模拟代码，达到实现高精度加法，来给大家看看我的代码
#include <bits/stdc++.h> using namespace std; int main(){ char a[505],b[505]; cin>>a>>b; int alen,blen,sum[505],f=0,k=0; alen=strlen(a); blen=strlen(b); while(alen!=0||blen!=0) { int a1=0,b1=0; if(alen>0) { a1=a[--alen]-'0'; } if(blen>0) { b1=b[--blen]-'0'; } int t=a1+b1+f; f=t/10; if(t>9) { t=t%10;//这里是进位操作，千万不能漏 } sum[k++]=t; } if(f) { sum[k++]=1; } for(int i=k-1;i>=0;i--) { cout<<sum[i]; } return 0; }
是非常吻合流程图的，你们可以自己去试试，或者运行一下，这个高精度加法也可以去提交一下，另外思考一下高精度减法，减法和加法非常相似，区别就在于减法要注意退位的事，还有就是要注意可能有负数，记得加负号，接下来只要你能理解高精度加法的内容，就可以自己独立完成高精度减法，我可以再给大家一个思路（其实是一个竖式）
好，看了这个竖式后有没有豁然开朗的感觉？没有就对了自己试一试，也许就柳暗花明又一村了呢？
接下来，我们来讲乘法 其实乘法原理是一样的，都和加法一样，模拟出竖式的
运算，然后注意一下进位的问题就ok了，因为我知道你认真看到这已经很辛苦了，所以我就直接给出代码好了。
#include <bits/stdc++.h> #define N 2001 using namespace std; int main(){ string s1,s2; int a[N],b[N],c[2*N],la,lb; cin>>s1>>s2; la = s1.length(),lb=s2.length(); //cout<<la<<lb; for(int i=0;i<la;i++) a[i]=s1[la-i-1]-'0'; for(int i=0;i<lb;i++) b[i]=s2[lb-i-1]-'0'; for(int i=0;i<la;i++) for(int j=0;j<lb;j++) c[i+j]+=a[i]*b[j]; int l=la+lb; //cout<<l; //return 0; for(int i=0;i<l;i++) { c[i+1]+=c[i]/10; c[i]%=10; } while(c[l-1]==0&&l>1) l--; for(int i=l-1;i>=0;i--) { cout<<c[i]; } return 0; }
以上就是今天的内容了，你是不是感觉缺了什么，对，我还没写除法的，如果你还想学到关于除法的高精度算法，就请关注➕一下我，我会在下期开头公布答案，今天的课后练习就是自己把今天的高精度代码在编译器中写一遍。
如果你觉得我写的好，或喜欢我的0基础学算法系列，请你点赞?，和关注➕我，我会给大家带来更多的算法，下一期预告 第五弹 填坑！
如果你对我讲的有什么问题，你可以在评论区留言，我会在填天坑系列中解答所有的问题
