神经网络前向和后向传播推导(一):概览
大家好~本文介绍了前向传播、梯度下降和后向传播算法,总结了
神经网络在训练和推理阶段执行的步骤。
在后面的文章中,我们会从最简单的神经网络开始,不断地增加不同种类的层(如全连接层、卷积层、BN层等),推导每种层的前向传播、后向传播、梯度计算、权重和偏移更新的数学公式
神经元
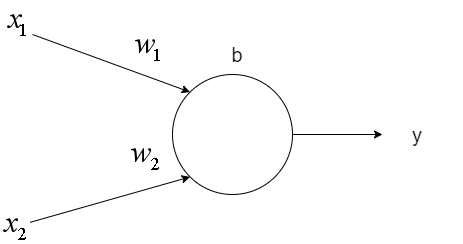
如上图所示,一个神经元具有一个偏移值b和多个权重值w,接受多个输入值x,返回一个输出值y
计算公式为:
\begin{equation}
y=f(\vec{w}\vec{x}+b)
\end{equation}其中\(\vec{w} = [w_1, w_2], \vec{x} = [x_1, x_2], f为激活函数\)
我们可以将\(b\)表示为\(w_b\),合并到\(\vec{w}\)中;并且把\(y\)表示为向量。这样就方便了向量化编程
计算公式变为:
\begin{equation}
\vec{y}=f(\vec{w}\vec{x})
\end{equation}其中\(\vec{w} = [w_b, w_1, w_2], \vec{x} = [1, x_1, x_2], \vec{y}=[y]\)
神经网络
一个神经网络由多层组成,而每层由多个神经元组成。
如下图所示是一个三层神经网络,由一层输入层+两层全连接层组成:
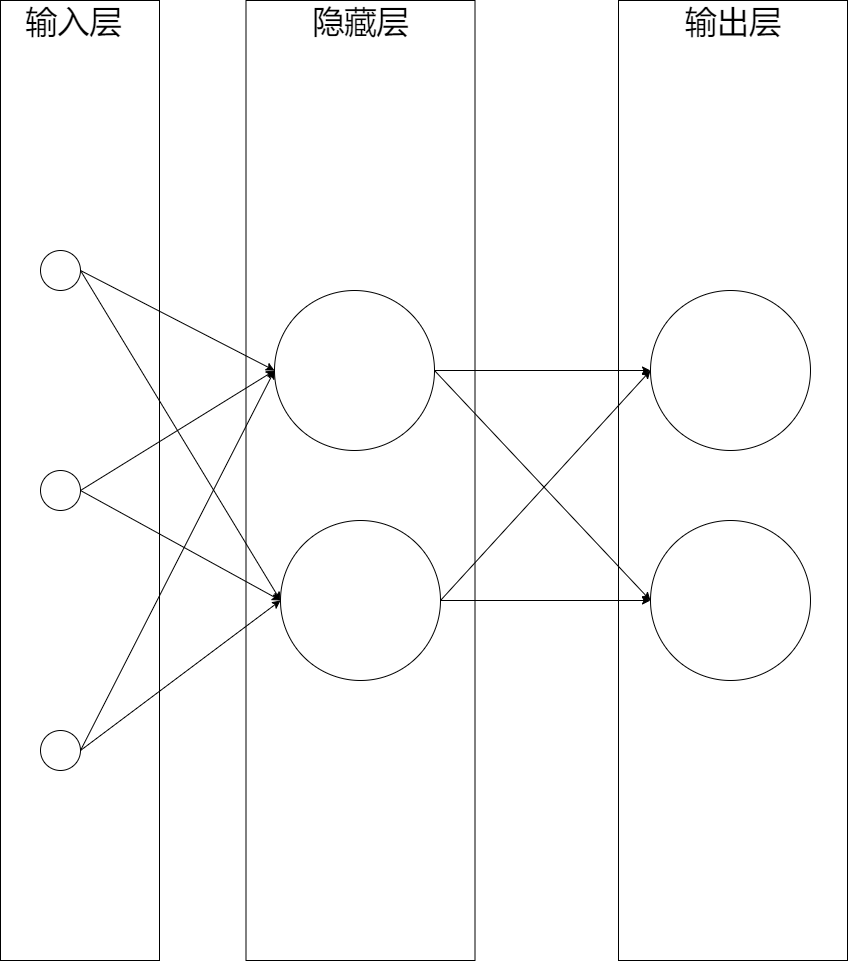
这个网络中最左边的层称为输入层,包含输入神经元;最右边的层称为输出层,包含输出神经元;中间的层则被称为隐藏层
前向传播
从输入层开始,输入层的输出作为隐藏层的输入传入隐藏层,计算出输出:\(\overrightarrow{y_{隐藏层}}\);
\(\overrightarrow{y_{隐藏层}}\)作为输出层的输入传入输出层,计算出输出:\(\overrightarrow{y_{输出层}}\),作为整个网络的输出。
这就是前向传播算法,也就是从输入层开始,依次传入每层,直到输出层,从而得到每层的输出。
前向传播用来做什么呢?它在训练和推理阶段都有使用:
在训练阶段,前向传播得到了输出层的输出和其余各层的输出,其中计算正确率需要前者,计算后向传播需要前者和后者;
在推理阶段,前向传播得到了输出层的输出,作为推理的结果。比如根据包含一个人的体重、身高这样的一个样本数据,得到了这人是男人还是女人的输出。
梯度下降
推理阶段使用前向传播得到输出值,而前向传播需要知道每层的权重和偏移。
为了在推理阶段能够得到接近真实值的输出值,每层的权重和偏移应该是某个合适的值。那么合适的值应该是多少呢?
我们可以在训练阶段给每层一个初始的权重和偏移(比如说都设为0);然后输入大量的样本,不断地更新每层的权重和偏移,使得它们逐渐接近合适的值。
那么,什么值才是合适的值呢?
我们可以构建一个目标函数,用来在训练阶段度量输出层的输出值和真实值的误差大小:
\begin{equation}
e=E(\overrightarrow{y_{输出层}}, \overrightarrow{y_{真实}})
\end{equation}其中\(\overrightarrow{y_{输出层}}\)为输出层的输出值,\(\overrightarrow{y_{真实}}\)为真实值,\(E\)为目标函数,\(e\)为误差
当误差\(e\)最小时,输出层的输出值就最接近真实值。因为\(E\)是输出层的权重和偏移(\(\overrightarrow{w_{输出层}}\)))的函数(因为\(E\)是\(\overrightarrow{y_{输出层}}\)的函数,而\(\overrightarrow{y_{输出层}}\)又是\(\overrightarrow{w_{输出层}}\)的函数,所以\(E\)是\(\overrightarrow{w_{输出层}}\)的函数),所以此时的\(\overrightarrow{w_{输出层}}\)就是合适的值
如何求\(E\)的最小值点呢?对于计算机来说,可以一步一步的去把函数的极值点试出来,如下图所示:
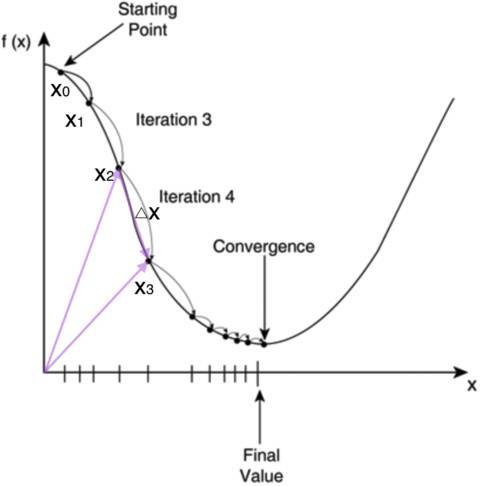
首先,我们随便选择一个点开始,比如上图的\(x_0\)。接下来,每次迭代修改\(X\)为\(x_1, x_2, x_3\)……经过数次迭代后最终达到函数最小值点。
你可能要问了,为啥每次修改\(X\),都能往函数最小值那个方向前进呢?这里的奥秘在于,我们每次都是向函数\(y=f(x)\)的梯度的相反方向来修改\(X\)。
什么是梯度呢?梯度是一个向量,它指向函数值上升最快的方向。显然,梯度的反方向当然就是函数值下降最快的方向了。
我们每次沿着梯度相反方向去修改\(X\),当然就能走到函数的最小值附近。
之所以是最小值附近而不是最小值那个点,是因为我们每次移动的步长不会那么恰到好处,有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺,如果选择小了,那么就会迭代很多轮才能走到最小值附近;如果选择大了,那可能就会越过最小值很远,收敛不到一个好的点上。
按照上面的讨论,我们就可以写出梯度下降算法的公式:
\begin{equation}
x_{new}=x_{old}-\eta\frac{df(x)}{dx}
\end{equation}其中\(\frac{df(x)}{dx}\)是梯度,\(\eta\)是步长,也称作学习率
我们现在是求目标函数\(E\)的最小值,所以将上述公式的函数\(f\)换成\(E\);
又因为\(E\)是\(\overrightarrow{w_{输出层}}\)的函数,所以将上述公式的\(x\)换成\(\overrightarrow{w_{输出层}}\),\(x_0\)替换为初始的权重和偏移
所以梯度下降算法可以写成:
\begin{equation}
\overrightarrow{w_{输出层new}}=\overrightarrow{w_{输出层old}}-\eta\frac{dE(w_{输出层})}{dw_{输出层}}
\end{equation}
总结一下:我们应该按照梯度下降算法,不断地更新\(\overrightarrow{w_{输出层}}\),最后使得目标函数\(E\)的值\(e\)最小(即接近0),然后就停止训练,此时的\(\overrightarrow{w_{输出层}}\)就是合适的值,
后向传播
那么对于输出层之前的每层,如何得到合适的权重和偏移呢?
还是以之前给的三层神经网络为例:
因为隐藏层的输出是隐藏层的权重和偏移的函数,而
输出层的输出是隐藏层的输出的函数(隐藏层的输出是输出层的输入),并且而\(E\)是输出层的输出的函数,所以\(E\)是隐藏层的权重和偏移的函数
所以我们仍然使用梯度下降算法来更新隐藏层的权重和偏移,公式为:
\begin{equation}
\overrightarrow{w_{隐藏层new}}=\overrightarrow{w_{隐藏层old}}-\eta\frac{dE(w_{隐藏层})}{dw_{隐藏层}}
\end{equation}
不过这里需要先计算输出层的梯度,然后反向依次计算每个层(如隐藏层)的梯度,直到与输入层相连的层,这就是反向传播算法。
(在后面推导隐藏层后向传播的文章中,会使用全导数公式,那时候就会很清楚为什么要反向计算梯度了)
总结
神经网络的使用可以分成两个阶段:
训练和推理
训练阶段
先进行前向传播,得到每层的输出;
然后进行后向传播,得到每层的梯度;
最后按照梯度下降算法,更新每层的权重和偏移。
可以用下面的公式来表达训练:
每层的权重和偏移=训练(大量的样本)
\begin{equation}
W=训练(\sum_{} \overrightarrow{样本_i})
\end{equation} 其中\(W\)为包含每层的权重和偏移向量的矩阵
推理阶段
使用训练阶段得到的每层的权重和偏移,进行前向传播,得到输出层的输出作为推理结果。
可以用下面的公式来表达推理:
\begin{equation}
\overrightarrow{y_{输出层}}=推理(\overrightarrow{样本_i}, W)
\end{equation}
参考资料
零基础入门深度学习 | 第二章:线性单元和梯度下降
零基础入门深度学习 | 第三章:神经网络和反向传播算法


