手把手教你实现栈以及C#中Stack源码分析

2021 年 9 月 22 日
笔记
算法

定义

栈又名堆栈，是一种操作受限的线性表，仅能在表尾进行插入和删除操作。

它的特点是先进后出，就好比我们往桶里面放盘子，放的时候都是从下往上一个一个放（入栈），取的时候只能从上往下一个一个取（出栈），这个比喻并非十分恰当，比如拿盘子的时候只是习惯从上面开始拿，也可以从中间拿，而栈的话是只能操作最上面的元素，这样比喻只是为了便于了解。

刚开始接触栈可能会有些疑问，我们已经有数组和链表了，为什么还要栈这个操作受限制的数据结构呢？数组和链表虽然灵活，但是操作起来也更容易出错，而栈因为操作受限，在特定场景中使用还是有优势的。

当某个数据集合只涉及在一端插入和删除数据，并且满足先进后出的特性时，我们就应该首选“栈”这种数据结构。

栈的实现

栈的实现方式有两种，一种是基于数组实现的顺序栈，另一种是基于链表实现的链式栈。它的主要操作也就两个，即入栈和出栈，难度并不大😏。

先了解一下入栈（Push）和出栈（Pop），如下图

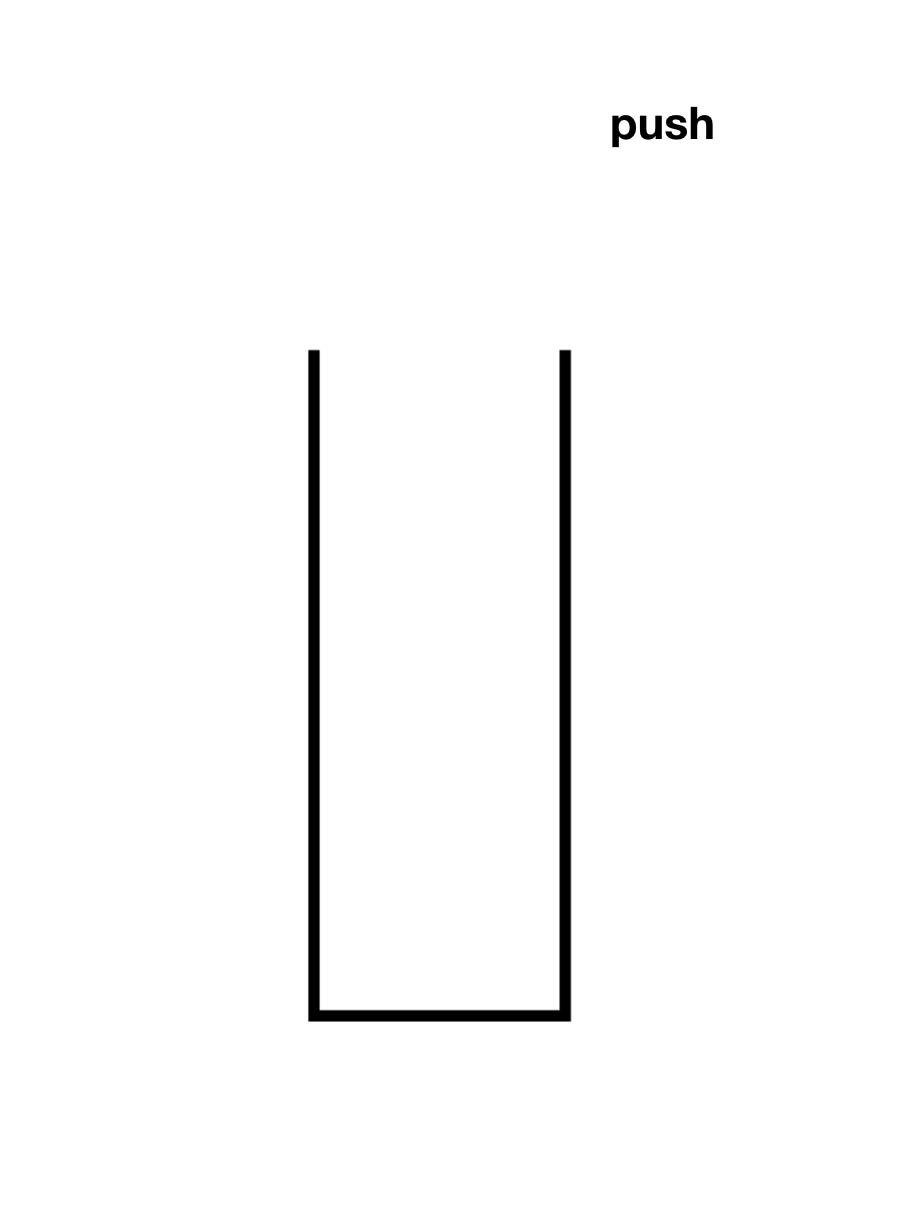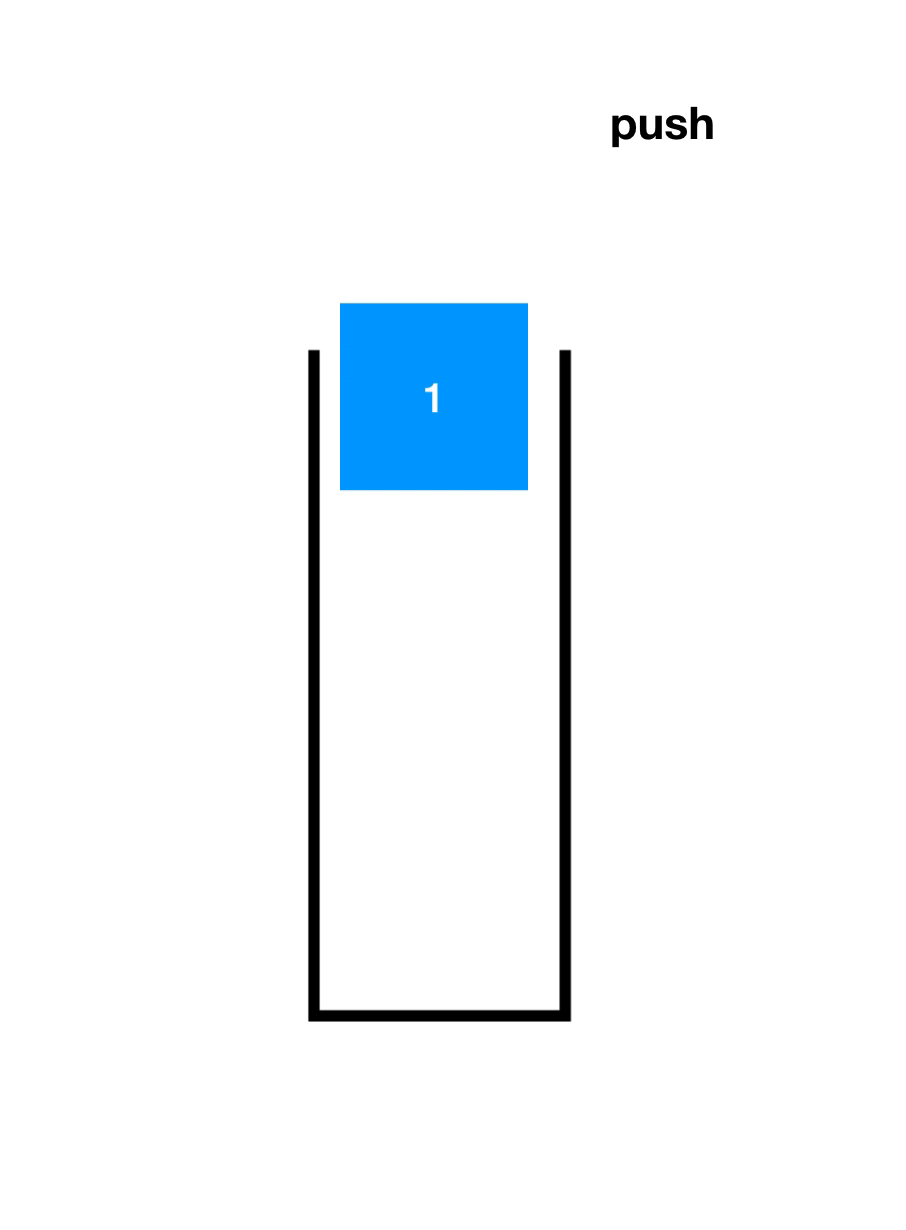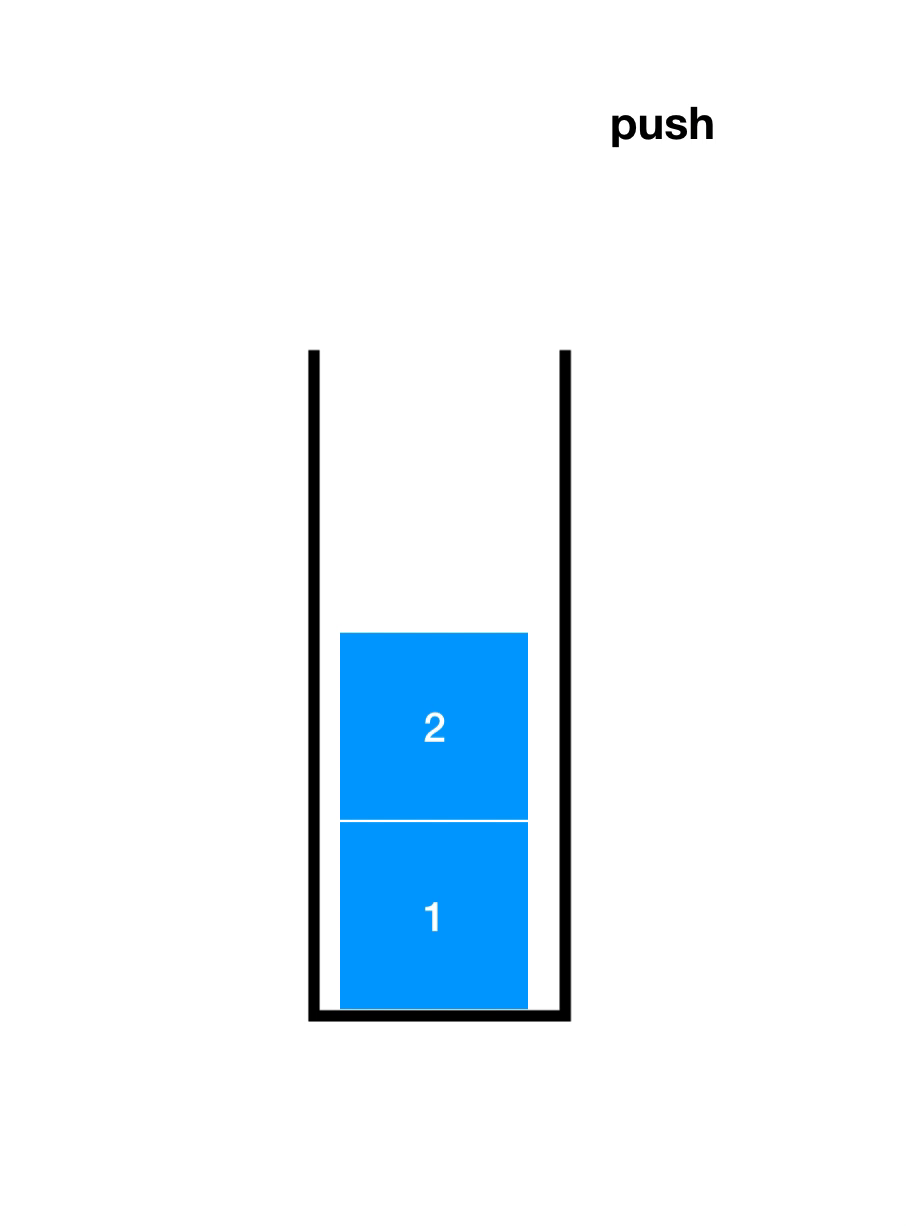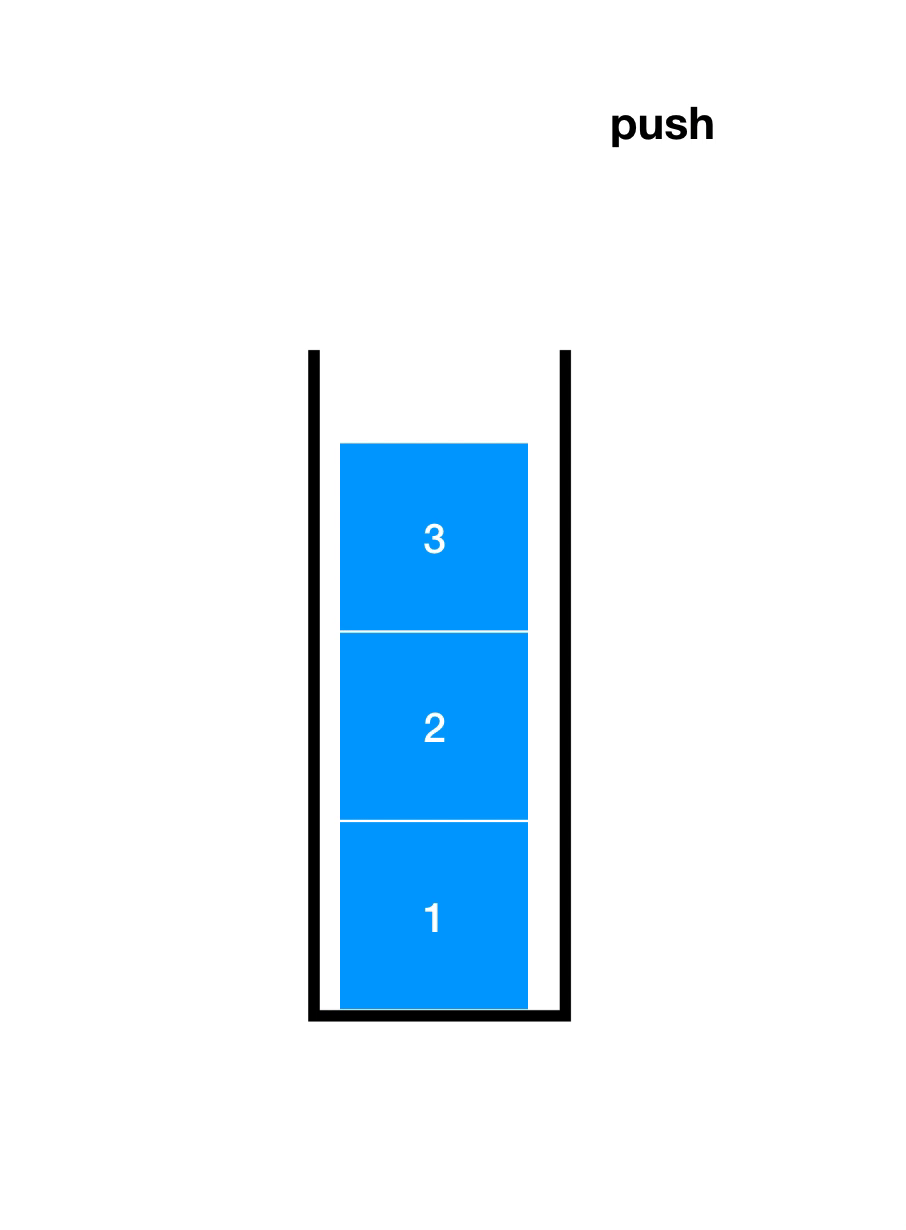
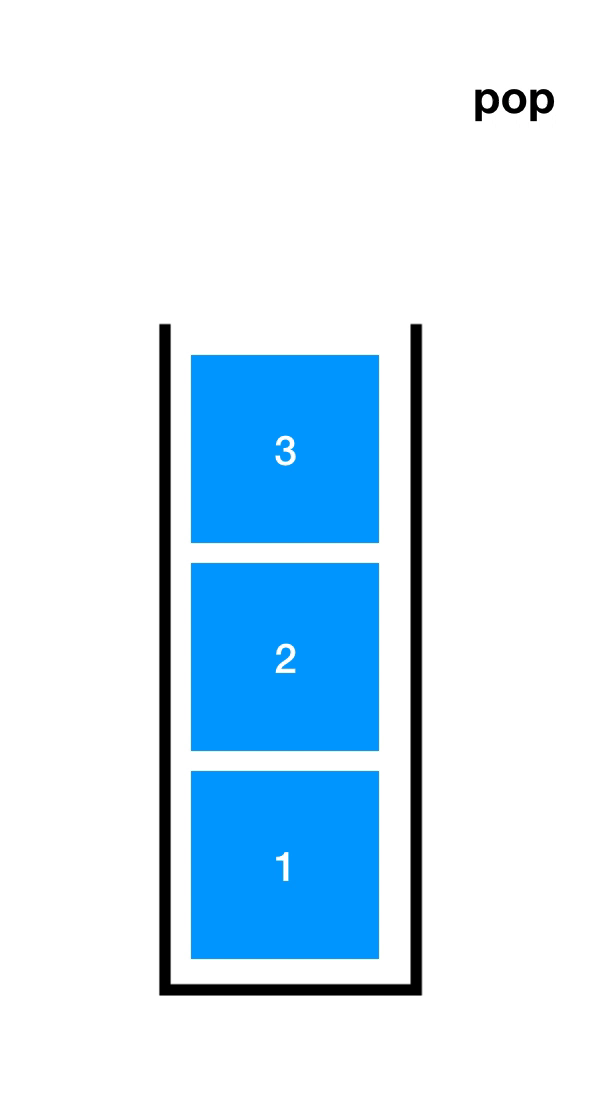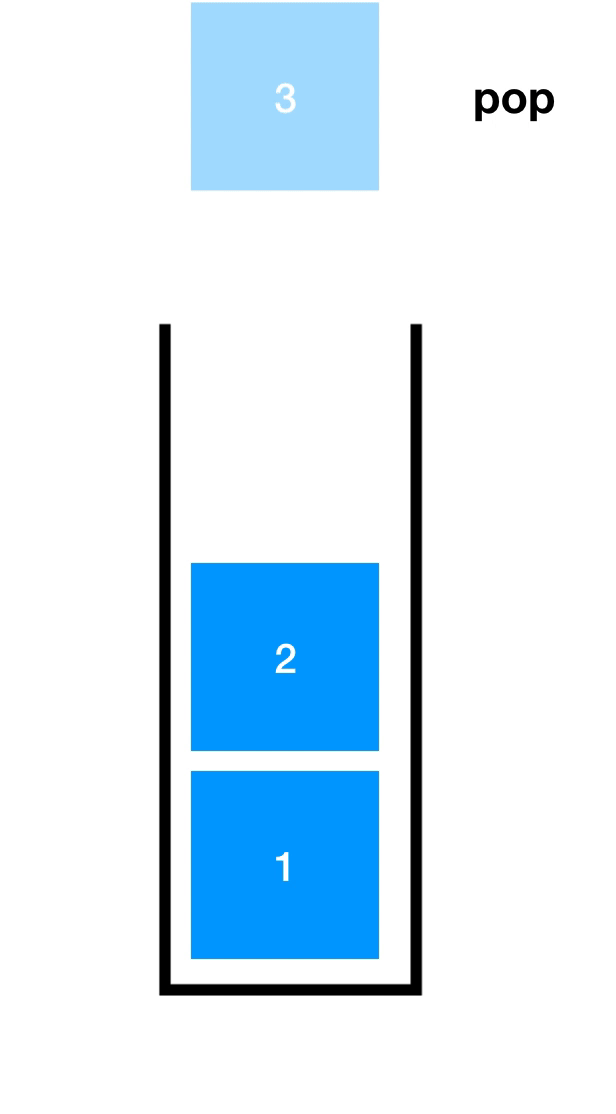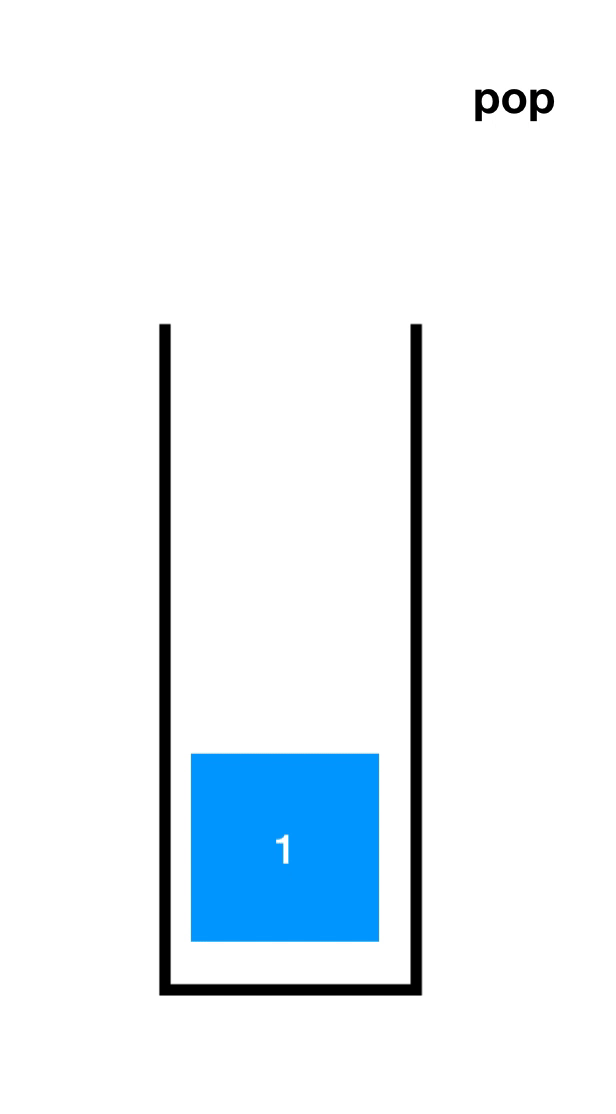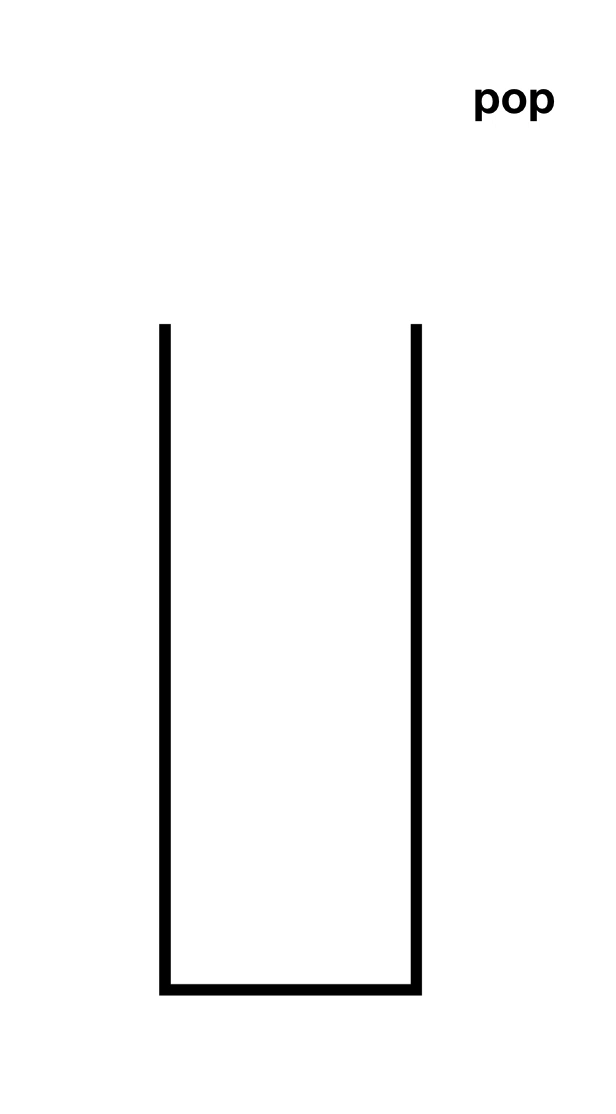
顺序栈

基于数组实现，就面临着数组大小固定、扩容成本大的问题，下面是使用C#实现出栈和入栈简单功能代码。

    // 基于数组实现的顺序栈
    public class ArrayStack
    {
        private string[] items;  // 数组
        private int count;       // 栈中元素个数
        private int n;           //栈的大小

        // 初始化数组，申请一个大小为n的数组空间
        public ArrayStack(int n)
        {
            this.items = new string[n];
            this.n = n;
            this.count = 0;
        }

        // 入栈操作
        public bool Push(string item)
        {
            // 数组空间不够了，直接返回false，入栈失败。
            if (count == n) return false;
            // 将item放到下标为count的位置，并且count加一
            items[count] = item;
            ++count;
            return true;
        }

        // 出栈操作
        public string Pop()
        {
            // 栈为空，则直接返回null
            if (count == 0) return null;
            // 返回下标为count-1的数组元素，并且栈中元素个数count减一
            string tmp = items[count - 1];
            --count;
            return tmp;
        }
    }

上面代码有一些很明显的缺点，比如存储的数据类型固定为string(C#中使用泛型可以很好的解决)，大小固定…这只是简单的功能演示，后面分析C#中Stack源码时这些问题都会被化解。

出栈和入栈的时间复杂度是多少呢？这个很好计算，因为出栈和入栈都只涉及栈顶的元素，所以是O(1)。

空间复杂度呢？还是O(1),因为这里只额外使用了count和n两个临时变量。

💁‍♂ 空间复杂度是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。例子中大小为n的数组是无法省略的，也就是说这n个空间是必须的，对复杂度不了解的可以点击查看一文搞定算法复杂度分析。

链式栈

话不多说，上代码

    // 链表实现栈
    public class LinkStack<T>
    {
        //栈顶指示器
        public Node<T> Top { get; set; }

        //栈中结点的个数
        public int NCount { get; set; }

        //初始化
        public LinkStack()
        {
            Top = null;
            NCount = 0;
        }

        //获取栈的长度
        public int GetLength()
        {
            return NCount;
        }

        //判断栈是否为空
        public bool IsEmpty()
        {
            if ((Top == null) && (0 == NCount))
            {
                return true;
            }
            return false;
        }

        //入栈
        public void Push(T item)
        {
            Node<T> p = new Node<T>(item);
            if (Top == null)
            {
                Top = p;
            }
            else
            {
                p.Next = Top;
                Top = p;
            }
            NCount++;
        }

        //出栈
        public T Pop()
        {
            if (IsEmpty())
            {
                return default(T);
            }
            Node<T> p = Top;
            Top = Top.Next;
            --NCount;
            return p.Data;
        }
    }

    //结点定义
    public class Node<T>
    {
        public T Data;

        public Node<T> Next;

        public Node(T item)
        {
            Data = item;
        }
    }

时间复杂度和空间复杂度均为O(1).

C#中Stack源码分析

前面我们已经知道了顺序栈和链式栈的优缺点，那么C#语言中自带的Stack是基于什么实现的呢？

答案是顺序栈。Stack是一个泛型类，里面定义了一个泛型数组用以存储数据

    private T[] _array;

既然是一个顺序栈，为什么在使用的过程中什么不需要初始化数组大小，也不用担心扩容问题呢？

当我们实例化Stack的时候，会调用它的构造函数，初始化数组大小为0.

    public Stack()
    {
        _array = _emptyArray;
        _size = 0;
        _version = 0;
    }

向数组中添加元素时，会检测数组是否还有空闲容量，如果超出数组大小，将进行扩容

    public void Push(T item)
    {
        if (_size == _array.Length)
        {
            T[] array = new T[(_array.Length == 0) ? 4 : (2 * _array.Length)];
            Array.Copy(_array, 0, array, 0, _size);
            _array = array;
        }

        _array[_size++] = item;
        _version++;
    }

正是因为C#帮我们封装好了，所以我们使用起来才感觉如此的方便。

Push()函数的时间复杂度是多少呢？当栈中有空闲空间时，可以直接添加，它的时间复杂度是O(1)。但当内存不够需要扩容时，需要重新申请内存，进行数据搬移，所以时间复杂度就变成了O(n)，其平均时间复杂度也为O(1).

总结

Tags: 算法