基于循环队列的BFS的原理及实现
- 2021 年 1 月 27 日
- 笔记
文章首发于微信公众号:几何思维
1.故事起源
有一只蚂蚁出去寻找食物,无意中进入了一个迷宫。蚂蚁只能向上、下、左、右4个方向走,迷宫中有墙和水的地方都无法通行。这时蚂蚁犯难了,怎样才能找出到食物的最短路径呢?
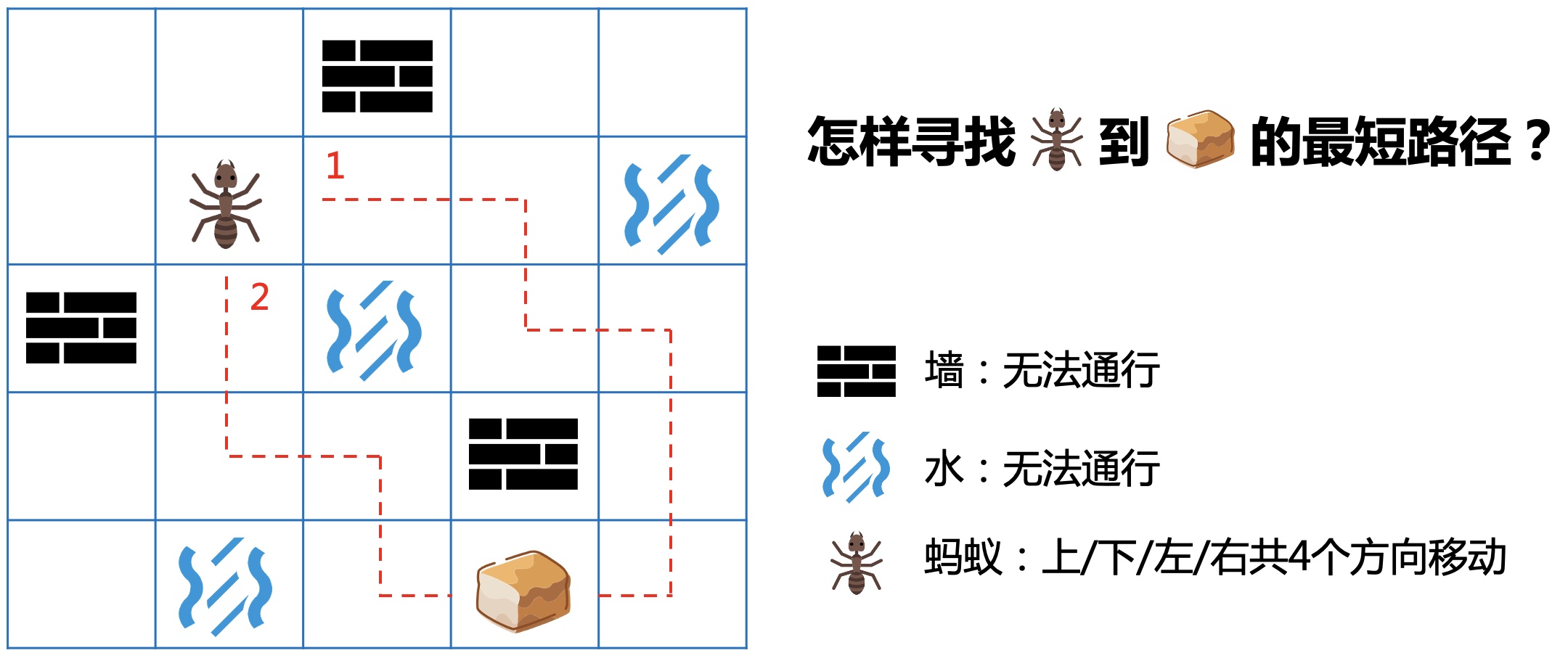
2.思考
蚂蚁在起点时,有4个选择,可以向上、下、左、右某一个方向走1步。
如果蚂蚁走过了一段距离,此时也依然只有4个选择。
当然要排除之前走过的地方(不走回头路,走了也只会更长)和无法通过的墙和水。

蚂蚁想,还好我会影分身。如果每一步都分身成4个蚂蚁,向4个方向各走1步,这样最先找到食物的肯定就是最短的路径了(因为每一步都把能走的地方都走完了,肯定找不出更短的路径了)。
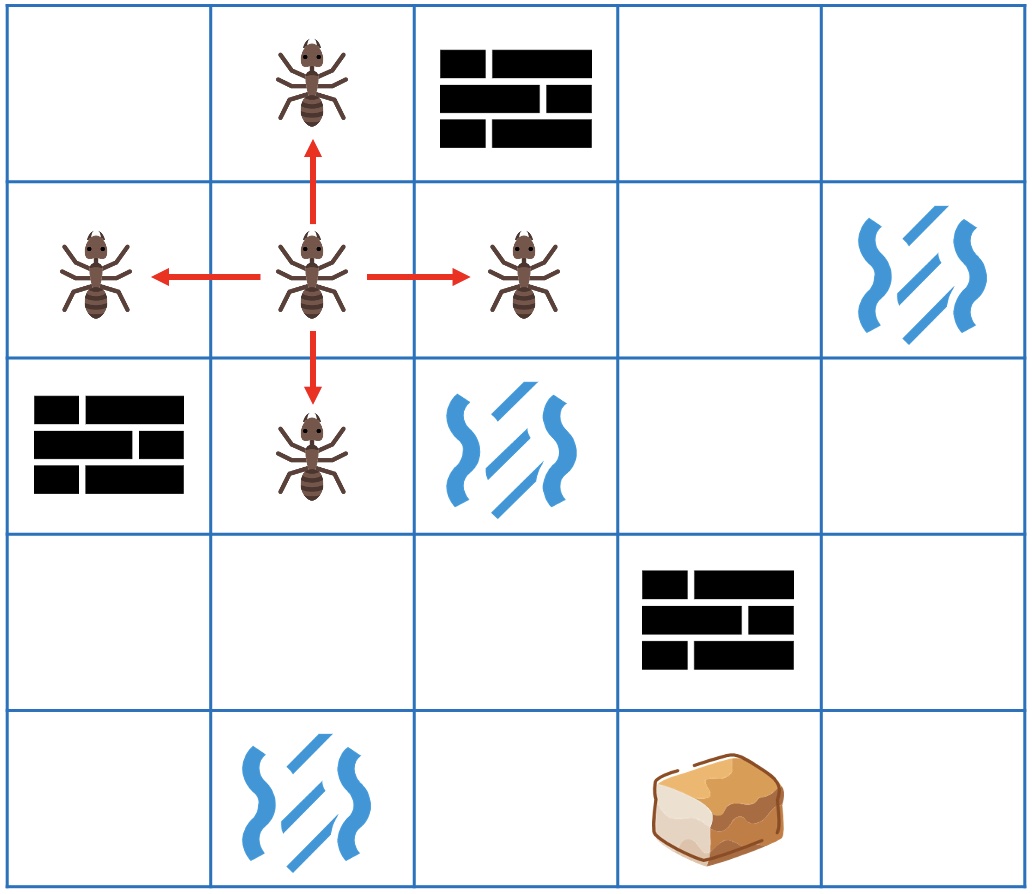
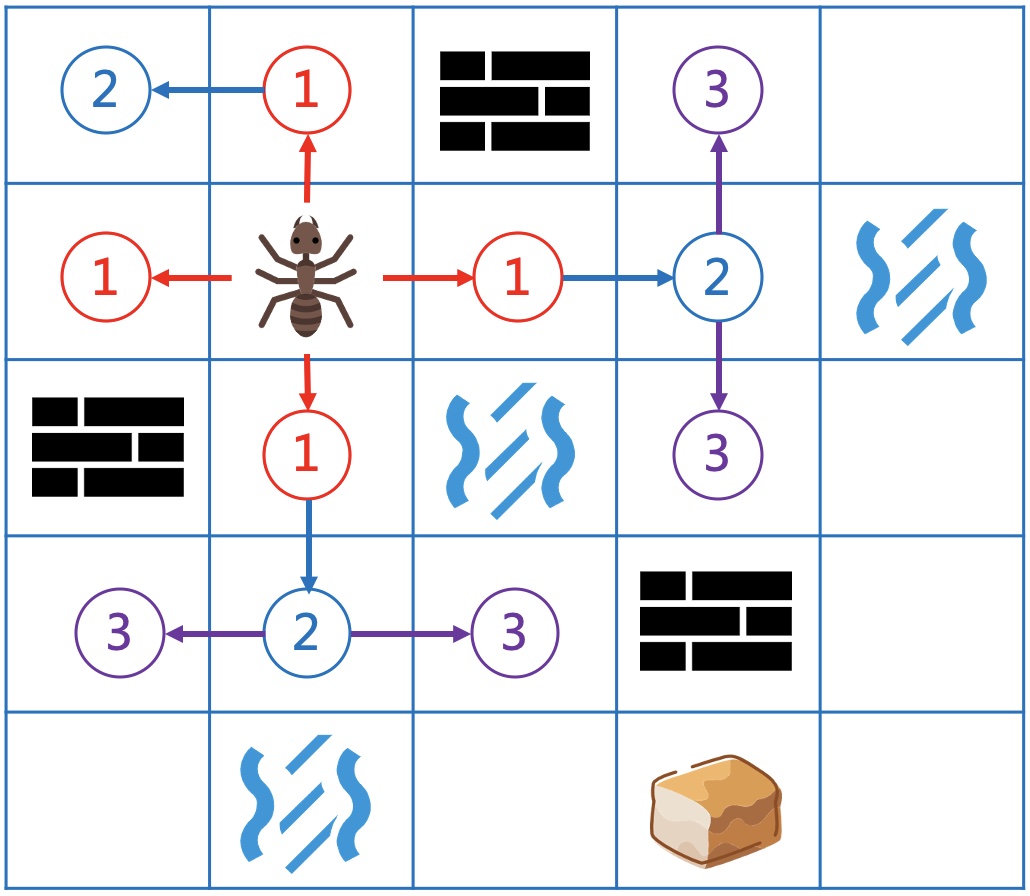
而且还能看出,第1步会到达所有到起点距离为1的地方,第2步也会到达所有距离为2的地方。
如此类推,第n步会覆盖所有到起点最短距离为n的地方。
3.问题建模
把迷宫地图放在二维数组中,能通行的地方为0,墙和水的地方为负数。
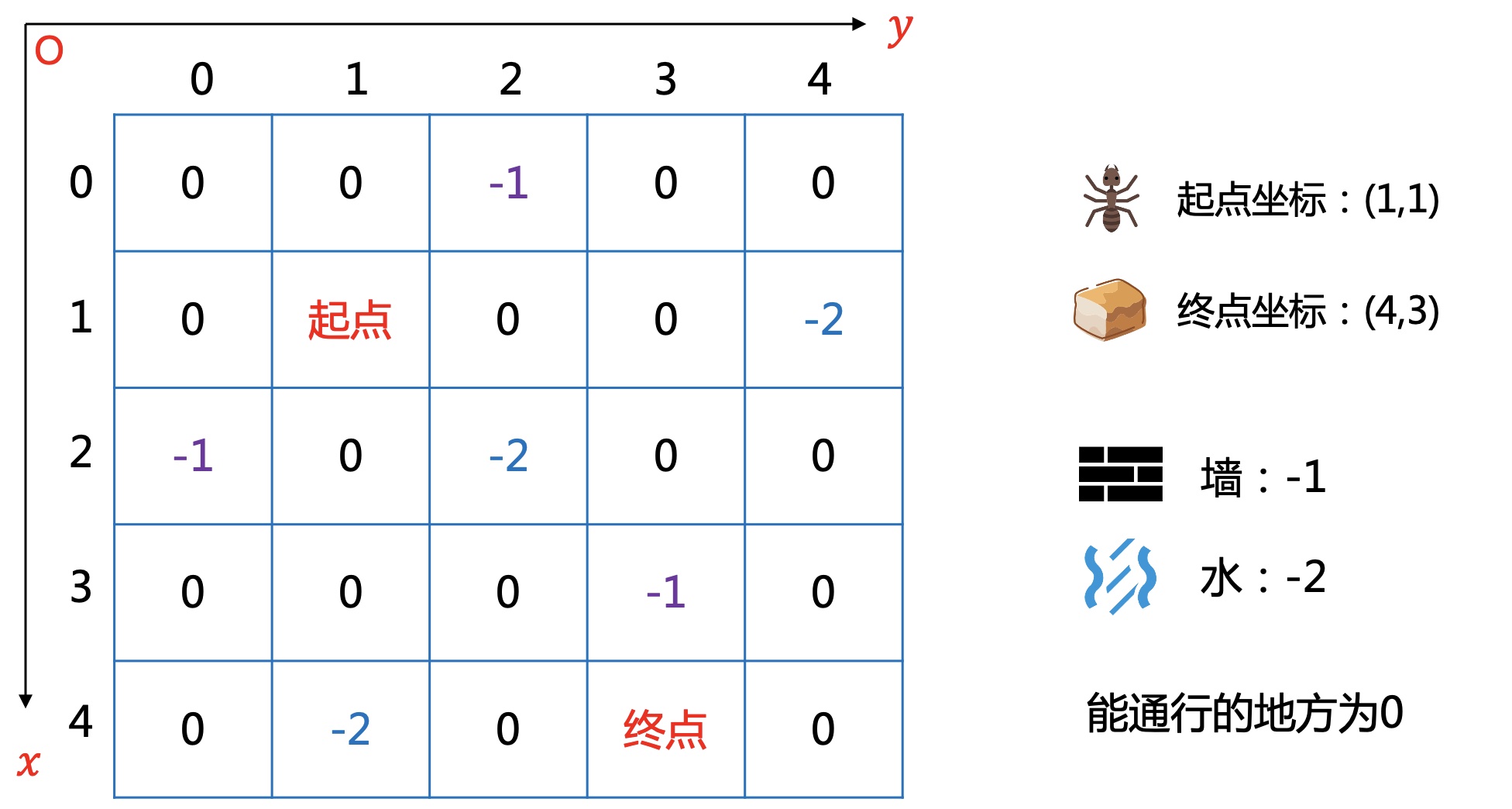
每一步向4个方向走,可以通过当前坐标\((x,y)\)加上一个方向向量。
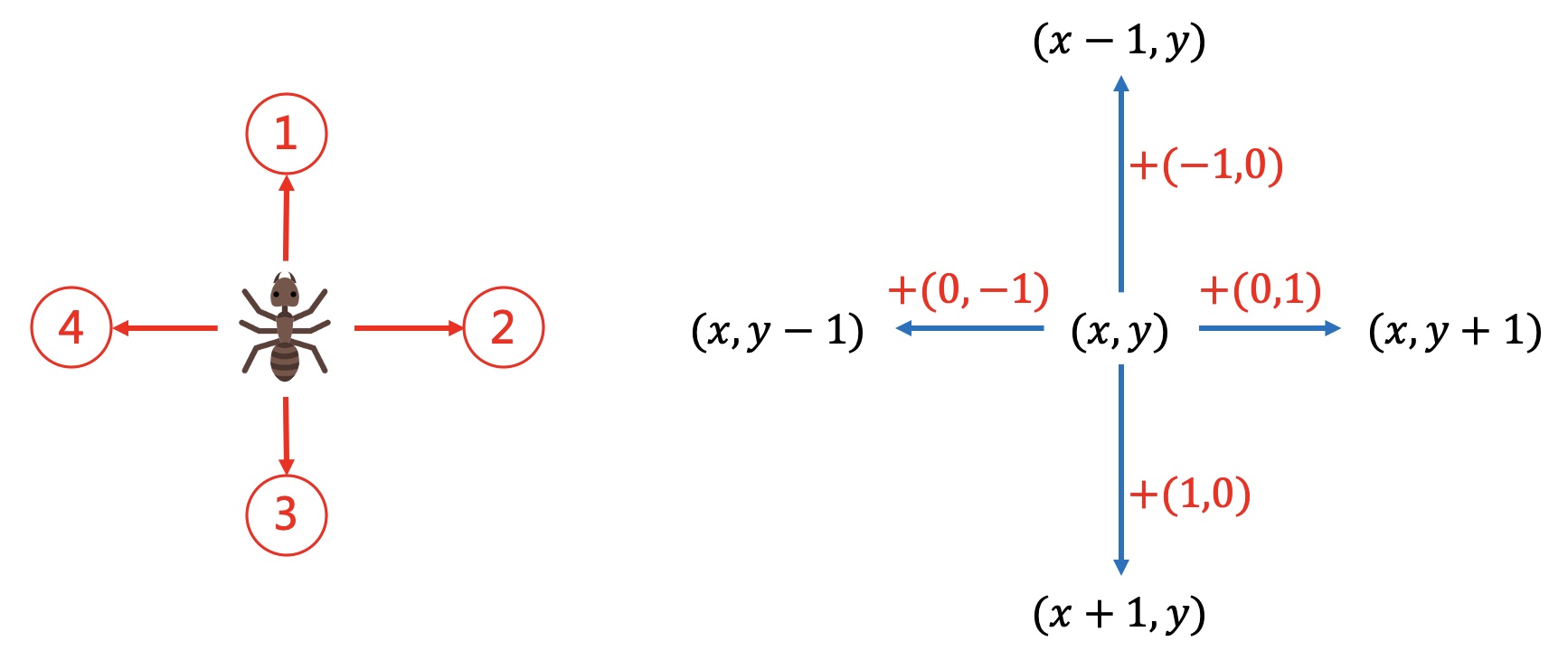
这个其实就是宽度优先搜索(BFS)的思想。
4.宽度优先搜索(BFS)
又称广度优先搜索,优先向四周扩展子节点,是最简便的图的搜索算法之一,一般通过队列来实现。
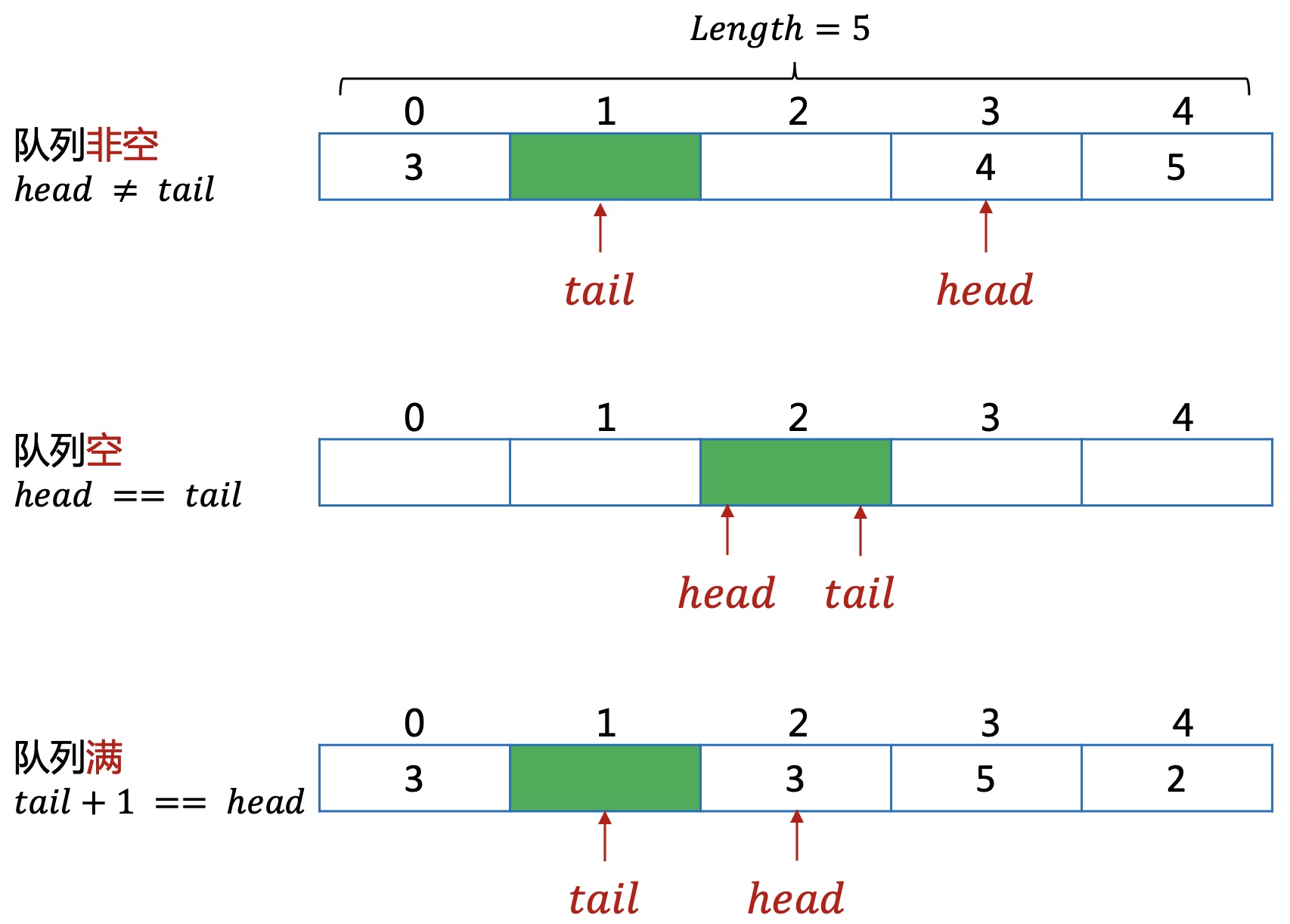
4.1 队列
是一种特殊的线性表,它只允许在表的前端进行删除操作,而在表的后端进行插入操作,即先进先出。
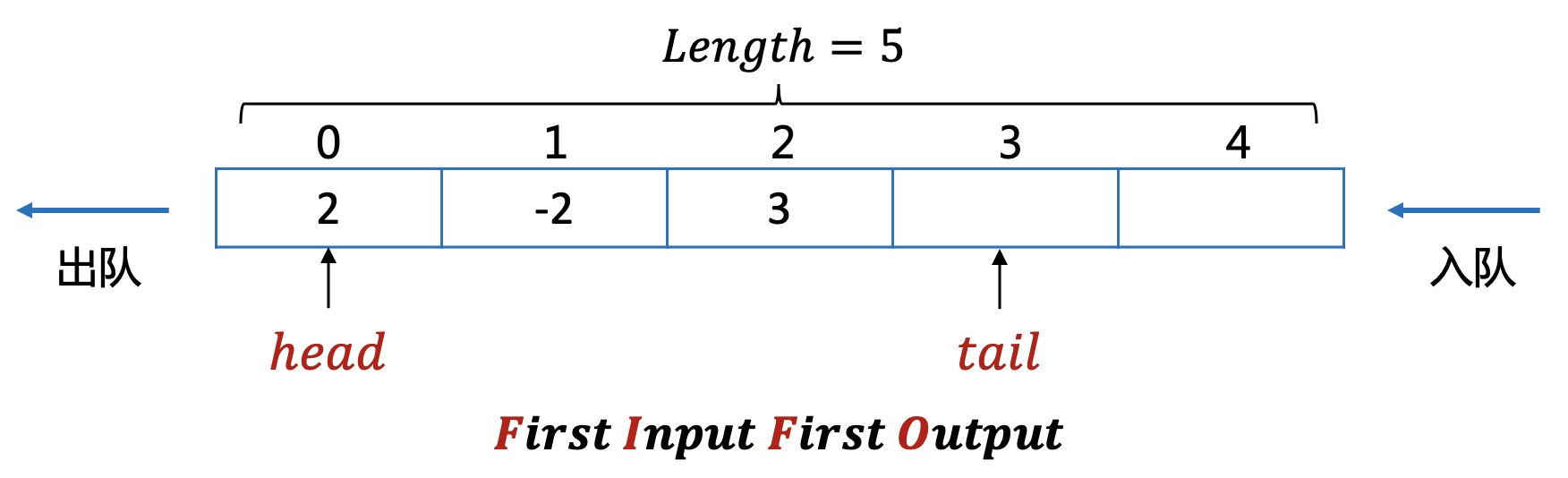
队列一般通过数组实现,对该数组增加一些操作上的限制。
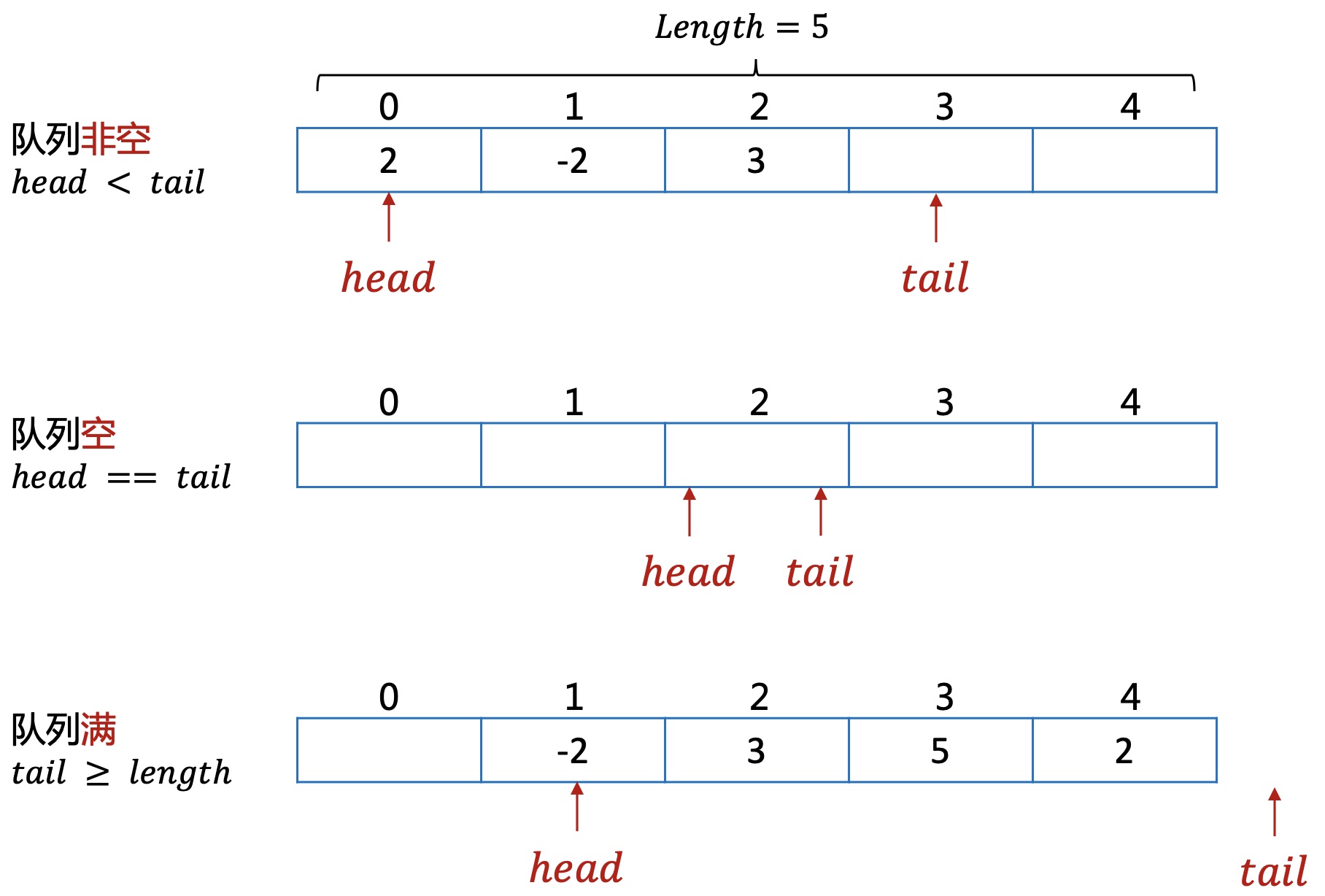
但上面的实现有一些缺陷,当队列满时,也就是tail指针移动到队尾,这时就无法再插入数据,但前面的元素已经出队了,可能还有空缺的位置。
为了能高效利用空间,对该队列增加一点改进,也就是循环队列的产生。
4.2 循环队列
把队列想象成一个首尾相接的环形。
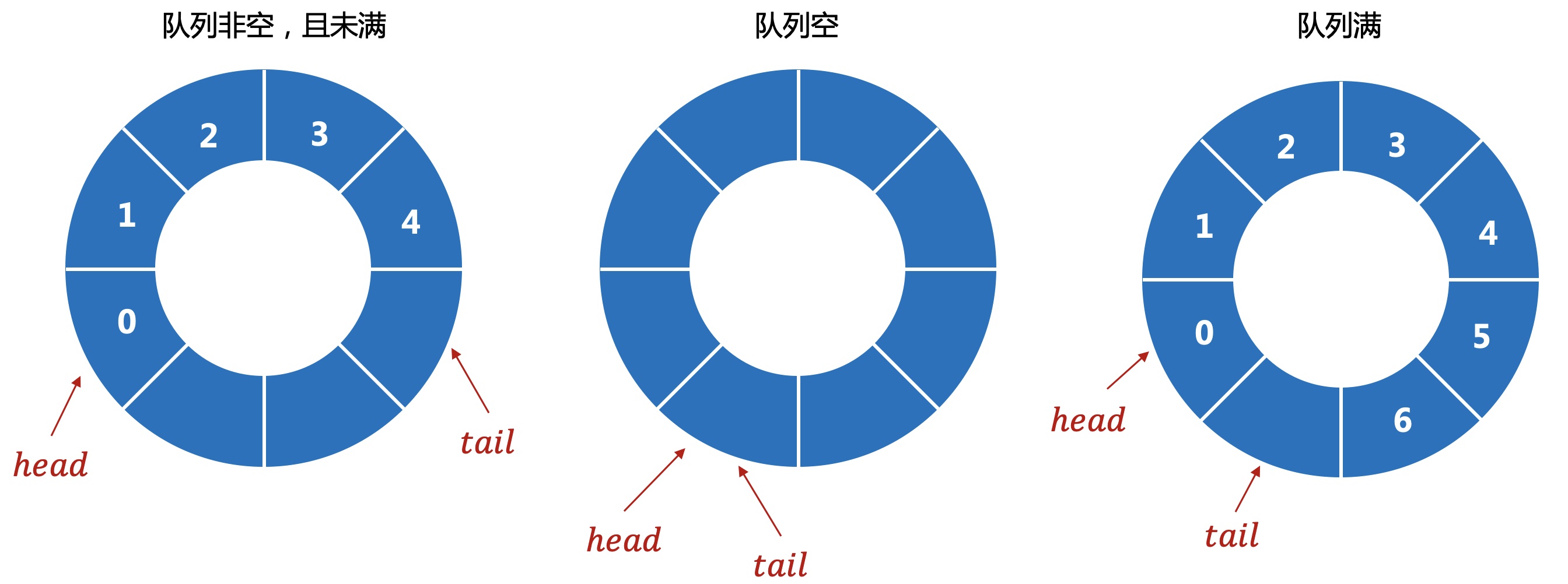
数组实现,需要多预留一个空间。如果head=tail时,无法判断是队空还是队满,所以占用一个空间,通过tail+1与head的关系来判断是否队满。
4.3 队列实现BFS
实现步骤如下:
- 将起点加入队列。
- 从队首取出一个节点,通过该节点向4个方向扩展子节点,并依次加入队尾。
- 重复以上步骤,直至队空或已找到目标位置。
回归迷宫问题,到起点的距离为1,2,3…的点会依次入队。
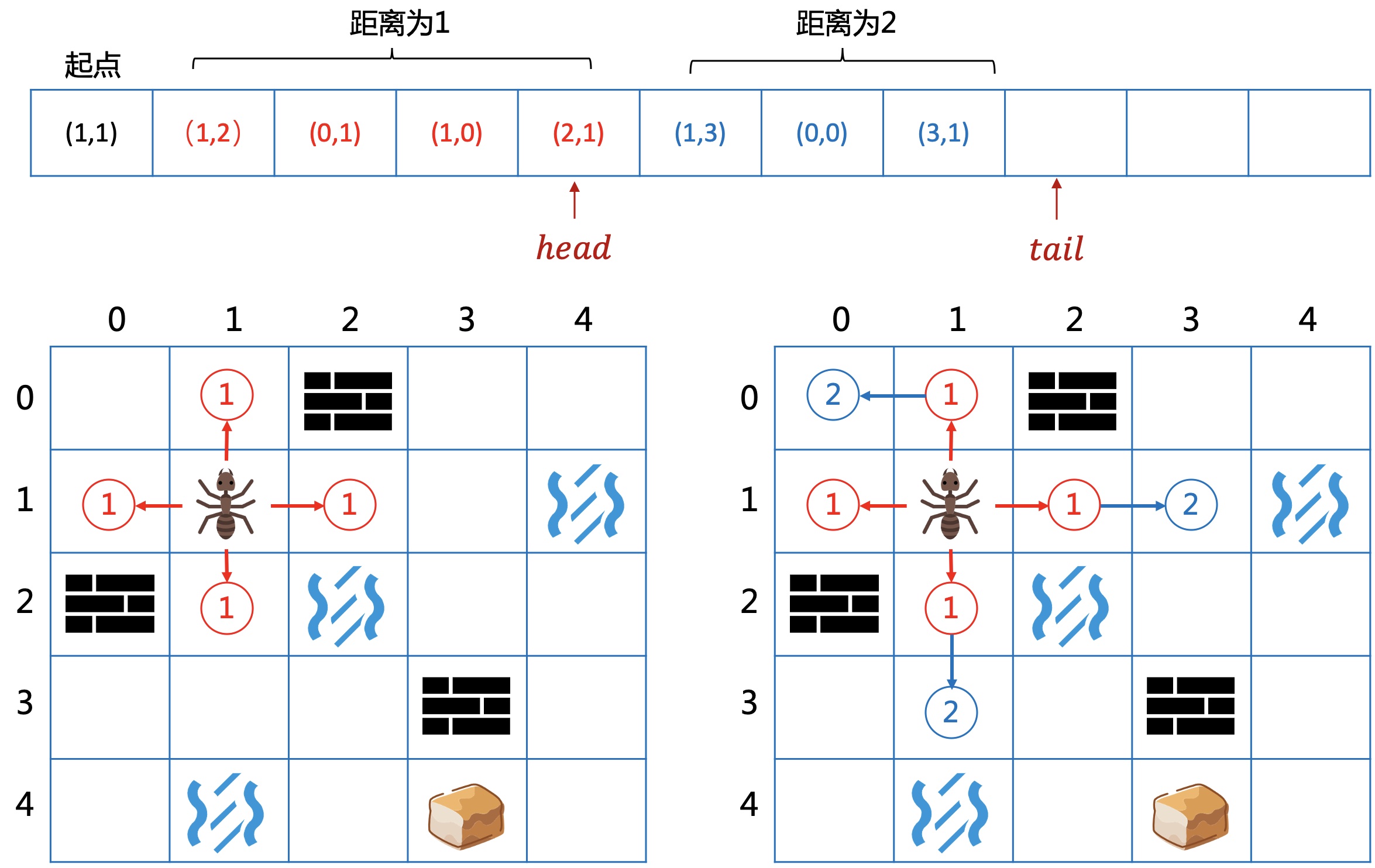
当head指针遍历到距离为2的点时,向4周扩展距离为3的节点,并继续入队。
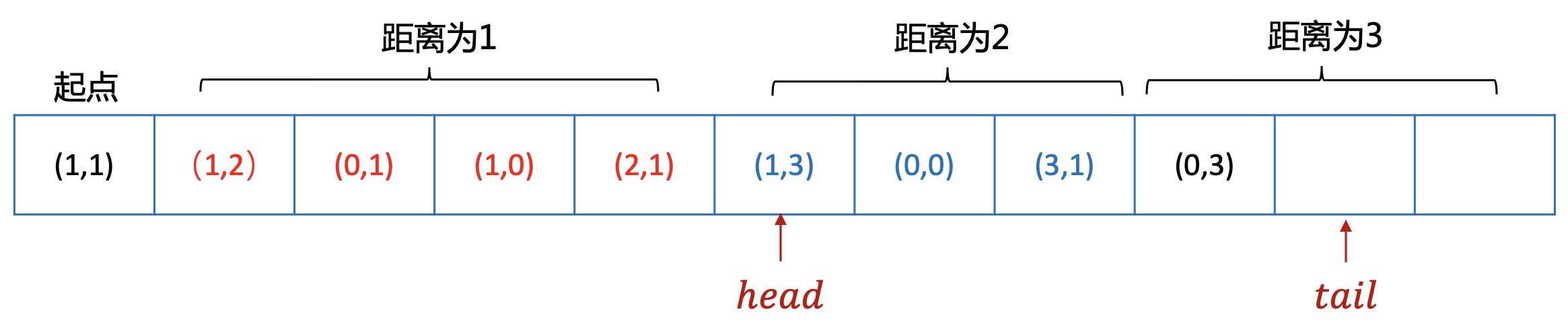
5.代码实现
5.1 变量定义
// 方向向量
const int direction[4][2] = {{0, 1},
{-1, 0},
{0, -1},
{1, 0}};
const int MAXM = 100, MAXN = 100, QUEUE_LENGTH = 5;
// 队列中的节点
struct Node {
int x, y, distance;
Node() {}
Node(int xx, int yy, int d) : x(xx), y(yy), distance(d) {}
};
int n, m, step = 0, map[MAXM][MAXN], visit[MAXM][MAXN];
Node start, target;
5.2 BFS标准模板
void bfs() {
Node queue[QUEUE_LENGTH];
int head = 0, tail = 1;
queue[0] = Node(start.x, start.y, 0);
visit[start.x][start.y] = 0;
while (head != tail) {
int x = queue[head].x;
int y = queue[head].y;
int distance = queue[head].distance;
head = (head + 1) % QUEUE_LENGTH;
for (int i = 0; i < 4; ++i) {
int dx = x + direction[i][0];
int dy = y + direction[i][1];
if (dx >= 0 && dx < m && dy >= 0 && dy < n && visit[dx][dy] == -1 && map[dx][dy] >= 0) {
// 表示从i方向走过来的,方便后续回溯路径
visit[dx][dy] = i;
if (dx == target.x && dy == target.y) {
cout << "已到目标点,最短距离为" << distance + 1 << endl;
step = distance + 1;
return;
}
if ((tail + 1) % QUEUE_LENGTH == head) {
cout << "队列满" << endl;
return;
}
// 新坐标入队
queue[tail] = Node(dx, dy, distance + 1);
tail = (tail + 1) % (QUEUE_LENGTH);
}
}
}
}
5.3 路径回溯
void printPath() {
int x, y, d, path[MAXM][MAXN] = {0};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
path[i][j] = -1;
}
}
x = target.x;
y = target.y;
path[start.x][start.y] = 0;
// 路径回溯
while (!(x == start.x && y == start.y)) {
path[x][y] = step--;
d = visit[x][y];
x -= direction[d][0];
y -= direction[d][1];
}
// 路径打印
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (path[i][j] >= 0) {
cout << path[i][j];
} else {
cout << "-";
}
}
cout << endl;
}
}
5.4 数据输入
int main() {
cin >> m >> n;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
cin >> map[i][j];
visit[i][j] = -1;
}
}
cin >> start.x >> start.y >> target.x >> target.y;
bfs();
if (step > 0) printPath();
return 0;
}
5.5 测试结果
输入数据:
5 5
0 0 -1 0 0
0 0 0 0 -2
-1 0 -2 0 0
0 0 0 -1 0
0 -2 0 0 0
1 1 4 3
输出:
已到目标点,最短距离为5
路径打印:
-----
-0---
-1---
-23--
--45-
扫描下方二维码关注公众号,第一时间获取更新信息!



