JavaScript实现树结构（二）

• 2020 年 3 月 11 日
• 笔记

JavaScript实现树结构（二）

一、二叉搜索树的封装

二叉树搜索树的基本属性：

如图所示：二叉搜索树有四个最基本的属性：指向节点的根（root），节点中的键（key）、左指针（right）、右指针（right）。

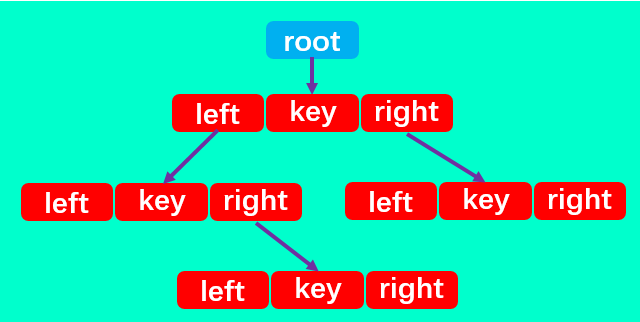
所以，二叉搜索树中除了定义root属性外，还应定义一个节点内部类，里面包含每个节点中的left、right和key三个属性：

    //封装二叉搜索树      function BinarySearchTree(){          //节点内部类        function Node(key){          this.key = key          this.left = null          this.right = null        }          //属性        this.root = null    }

二叉搜索树的常见操作：

• insert（key）：向树中插入一个新的键；
• search（key）：在树中查找一个键，如果节点存在，则返回true；如果不存在，则返回false；
• inOrderTraverse：通过中序遍历方式遍历所有节点；
• preOrderTraverse：通过先序遍历方式遍历所有节点；
• postOrderTraverse：通过后序遍历方式遍历所有节点；
• min：返回树中最小的值/键；
• max：返回树中最大的值/键；
• remove（key）：从树中移除某个键；

1.插入数据

实现思路：

• 首先根据传入的key创建节点对象；
• 然后判断根节点是否存在，不存在时通过：this.root = newNode，直接把新节点作为二叉搜索树的根节点。
• 若存在根节点则重新定义一个内部方法insertNode（）用于查找插入点。

     //insert方法:对外向用户暴露的方法        BinarySearchTree.prototype.insert = function(key){          //1.根据key创建节点          let newNode = new Node(key)            //2.判断根节点是否存在          if (this.root == null) {            this.root = newNode            //根节点存在时          }else {            this.insertNode(this.root, newNode)          }        }  

内部方法insertNode（）的实现思路:

根据比较传入的两个节点，一直查找新节点适合插入的位置，直到成功插入新节点为止。

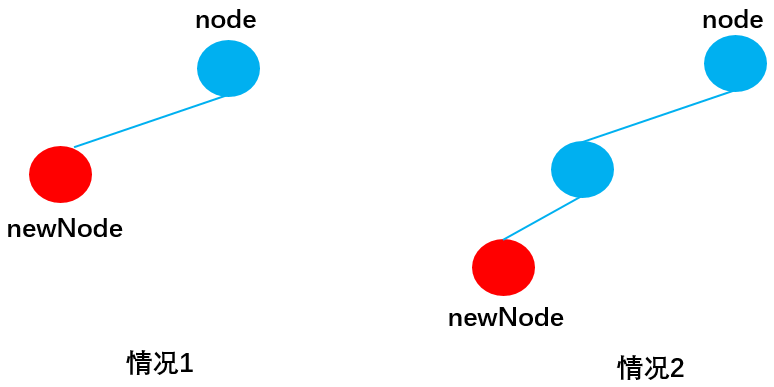
当newNode.key < node.key向左查找:

• 情况1：当node无左子节点时，直接插入：

• 情况2：当node有左子节点时，递归调用insertNode(),直到遇到无左子节点成功插入newNode后，不再符合该情况，也就不再调用insertNode()，递归停止。

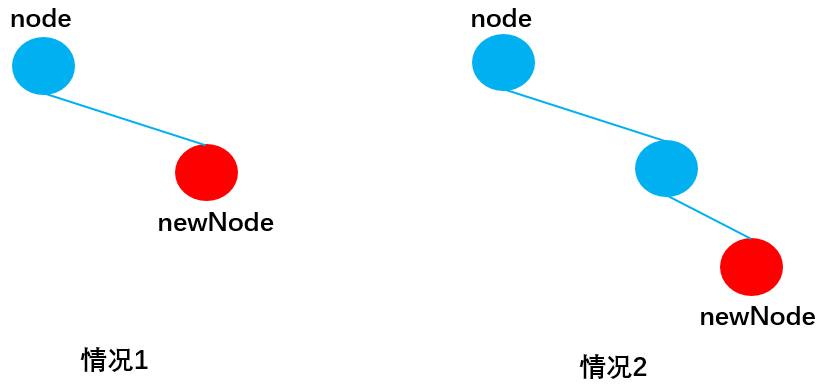
当newNode.key >= node.key向右查找，与向左查找类似：

• 情况1：当node无右子节点时，直接插入：

• 情况2：当node有右子节点时，依然递归调用insertNode(),直到遇到传入insertNode方法的node无右子节点成功插入newNode为止：

insertNode()代码实现：

      //内部使用的insertNode方法:用于比较节点从左边插入还是右边插入        BinarySearchTree.prototype.insertNode = function(node, newNode){          //当newNode.key < node.key向左查找  /*----------------------分支1:向左查找--------------------------*/          if(newNode.key < node.key){            //情况1：node无左子节点，直接插入  /*----------------------分支1.1--------------------------*/            if (node.left == null) {              node.left = newNode            //情况2：node有左子节点，递归调用insertNode(),直到遇到无左子节点成功插入newNode后，不再符合该情况，也就不再调用insertNode()，递归停止。  /*----------------------分支1.2--------------------------*/            }else{              this.insertNode(node.left, newNode)            }          //当newNode.key >= node.key向右查找  /*-----------------------分支2:向右查找--------------------------*/          }else{            //情况1：node无右子节点，直接插入  /*-----------------------分支2.1--------------------------*/            if(node.right == null){              node.right == newNode            //情况2：node有右子节点，依然递归调用insertNode(),直到遇到无右子节点成功插入newNode为止  /*-----------------------分支2.2--------------------------*/            }else{              this.insertNode(node.right, newNode)            }          }        }

过程详解：

为了更好理解以下列二叉搜索树为例：

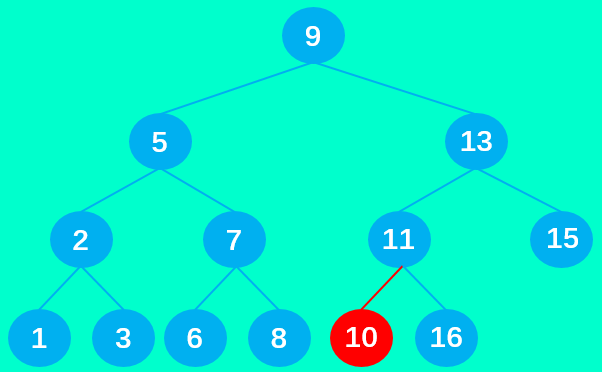
想要上述的二叉搜索树（蓝色）中插入数据10：

• 先把key = 10 传入insert方法，由于存在根节点 9，所以直接调用insetNode方法，传入的参数：node = 9，newNode = 10；
• 由于10 > 9，进入分支2，向右查找适合插入的位置；
• 由于根节点 9 的右子节点存在且为 13 ，所以进入分支2.2，递归调用insertNode方法，传入的参数：node = 13，newNode = 10；
• 由于 10 < 13 ，进入分支1，向左查找适合插入的位置；
• 由于父节点 13 的左子节点存在且为11，所以进入分支1.2，递归调用insertNode方法，传入的参数：node = 11，newNode = 10；
• 由于 10 < 11，进入分支1，向左查找适合插入的位置；
• 由于父节点 11 的左子节点不存在，所以进入分支1.1，成功插入节点 10 。由于不符合分支1.2的条件所以不会继续调用insertNode方法，递归停止。

测试代码：

    //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(9);      console.log(bst);

应得到下图所示的二叉搜索树：

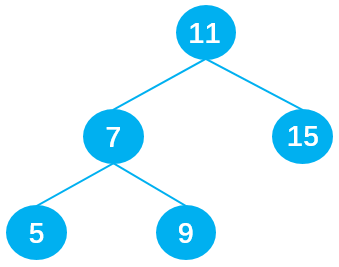
测试结果

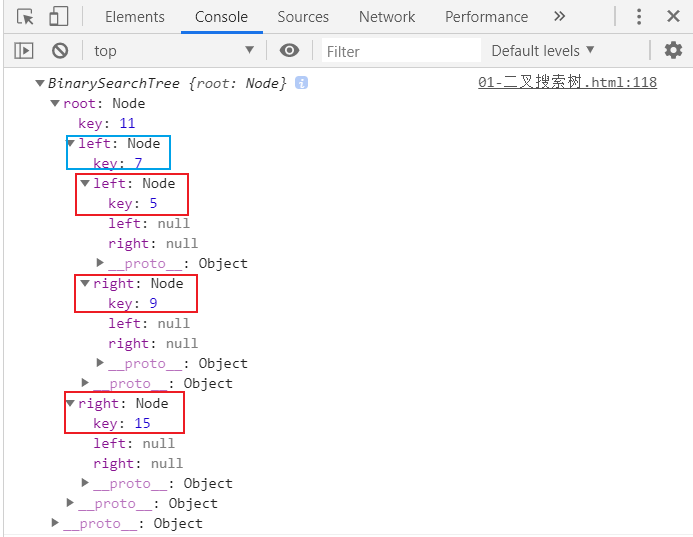
2.遍历数据

这里所说的树的遍历不仅仅针对二叉搜索树，而是适用于所有的二叉树。由于树结构不是线性结构，所以遍历方式有多种选择，常见的三种二叉树遍历方式为：

• 先序遍历；
• 中序遍历；
• 后序遍历；

还有层序遍历，使用较少。

2.1.先序遍历

先序遍历的过程为：

• 首先，遍历根节点；
• 然后，遍历其左子树；
• 最后，遍历其右子树；

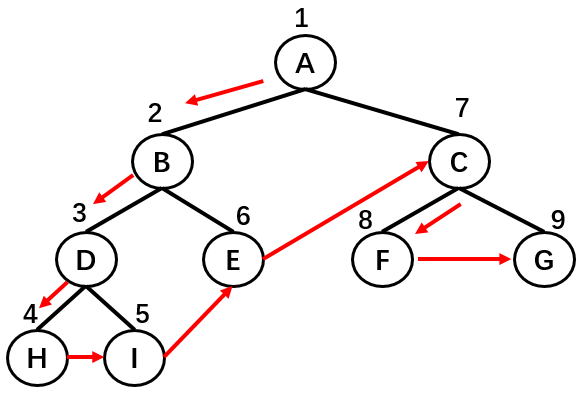
如上图所示，二叉树的节点遍历顺序为：A -> B -> D -> H -> I -> E -> C -> F -> G。

代码实现：

      //先序遍历        //掺入一个handler函数方便之后对得到的key进行处理        BinarySearchTree.prototype.preOrderTraversal = function(handler){          this.preOrderTraversalNode(this.root, handler)        }          //封装内部方法，对某个节点进行遍历        BinarySearchTree.prototype.preOrderTraversalNode = function(node,handler){          if (node != null) {            //1.处理经过的节点            handler(node.key)  /*----------------------递归1----------------------------*/            //2.遍历左子树中的节点            this.preOrderTraversalNode(node.left, handler)  /*----------------------递归2----------------------------*/            //3.遍历右子树中的节点            this.preOrderTraversalNode(node.right, handler)          }        }

过程详解：

以遍历以下二叉搜索树为例：

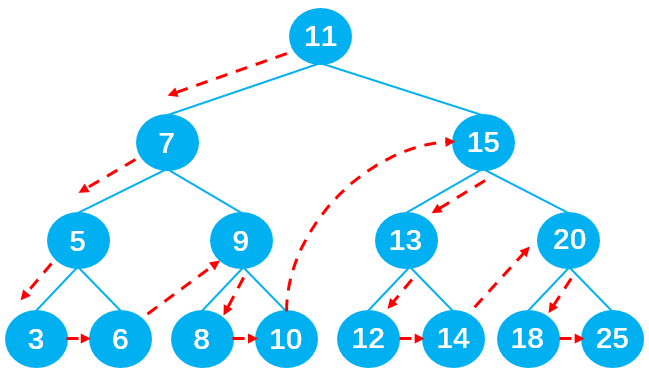
首先调用preOrderTraversal方法，在方法里再调用preOrderTraversalNode方法用于遍历二叉搜索树。在preOrderTraversalNode方法中，递归1负责遍历左子节点，递归2负责遍历右子节点。先执行递归1，执行过程如下图所示：

记：preOrderTraversalNode() 为 A()

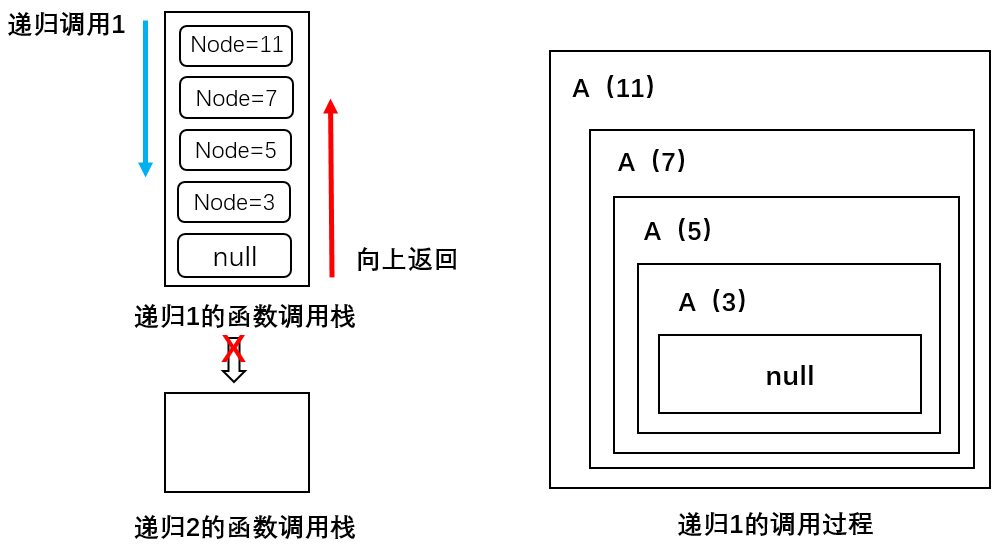
可以看到一共递归调用了4次方法A，分别传入11、7、5、3，最后遇到null不满足 node != null 条件结束递归1；注意此时只是执行完最开始的递归1，并没有执行递归2，并且递归1执行到null停止后要一层层地往上返回，按顺序将调用的函数压出函数调用栈。

关于函数调用栈：之前的四次递归共把4个函数压入了函数调用栈，现在递归执行完了一层层地把函数压出栈。

值得注意的是：每一层函数都只是执行完了递归1，当返回到该层函数时，比如A（3）要继续执行递归2遍历二叉搜索树中的右子节点；

在执行递归2的过程中会不断调用方法A，并依次执行递归1和递归2，以此类推直到遇到null不满足 node != null 条件为止，才停止递归并一层层返回，如此循环。同理A（5）层、A（7）层、A（11）层都要经历上述循环，直到将二叉搜索树中的节点全部遍历完为止。

具体过程如下图所示：

测试代码：

    //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);        //3.测试遍历      let resultString = ""      //掺入处理节点值的处理函数      bst.preOrderTraversal(function(key){        resultString += key + "->"      })      alert(resultString)

应输出这样的顺序：11 -> 7 -> 5 -> 3 -> 6 -> 9 -> 8 -> 10 -> 15 -> 13 ->12 -> 14 -> 20 -> 18 -> 25 。

测试结果：

2.2.中序遍历

实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

• 首先，遍历其左子树；
• 然后，遍历根（父）节点；
• 最后，遍历其右子树；

代码实现：

      //中序遍历        BinarySearchTree.prototype.midOrderTraversal = function(handler){          this.midOrderTraversalNode(this.root, handler)        }          BinarySearchTree.prototype.midOrderTraversalNode = function(node, handler){          if (node != null) {            //1.遍历左子树中的节点            this.midOrderTraversalNode(node.left, handler)              //2.处理节点            handler(node.key)              //3.遍历右子树中的节点            this.midOrderTraversalNode(node.right, handler)          }        }

过程详解：

遍历的顺序应如下图所示：

首先调用midOrderTraversal方法，在方法里再调用midOrderTraversalNode方法用于遍历二叉搜索树。先使用递归1遍历左子树中的节点；然后，处理父节点；最后，遍历右子树中的节点。

测试代码：

  //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);        //3.测试中序遍历      let resultString2 =""      bst.midOrderTraversal(function(key){        resultString2 += key + "->"      })      alert(resultString2)

输出节点的顺序应为：3 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18 -> 20 -> 25 。

测试结果：

2.3.后续遍历

实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

• 首先，遍历其左子树；
• 然后，遍历其右子树；
• 最后，遍历根（父）节点；

代码实现：

      //后序遍历        BinarySearchTree.prototype.postOrderTraversal = function(handler){          this.postOrderTraversalNode(this.root, handler)        }          BinarySearchTree.prototype.postOrderTraversalNode = function(node, handler){          if (node != null) {            //1.遍历左子树中的节点            this.postOrderTraversalNode(node.left, handler)              //2.遍历右子树中的节点            this.postOrderTraversalNode(node.right, handler)              //3.处理节点            handler(node.key)          }        }

过程详解：

遍历的顺序应如下图所示：

首先调用postOrderTraversal方法，在方法里再调用postOrderTraversalNode方法用于遍历二叉搜索树。先使用递归1遍历左子树中的节点；然后，遍历右子树中的节点；最后，处理父节点。

测试代码：

    //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);        //3.测试后序遍历      let resultString3 =""      bst.postOrderTraversal(function(key){        resultString3 += key + "->"      })      alert(resultString3)

输出节点的顺序应为：3 -> 6 -> 5 -> 8 -> 10 -> 9 -> 7 -> 12 -> 14 -> 13 -> 18 -> 25 -> 20 -> 15 -> 11 。

测试结果：

总结：以遍历根（父）节点的顺序来区分三种遍历方式。比如：先序遍历先遍历根节点、中序遍历第二遍历根节点、后续遍历最后遍历根节点。

3.查找数据

3.1.查找最大值&最小值

在二叉搜索树中查找最值非常简单，最小值在二叉搜索树的最左边，最大值在二叉搜索树的最右边。只需要一直向左/右查找就能得到最值，如下图所示：

代码实现：

      //寻找最大值        BinarySearchTree.prototype.max = function () {          //1.获取根节点          let node = this.root          //2.定义key保存节点值          let key = null          //3.依次向右不断查找，直到节点为null          while (node != null) {            key = node.key            node = node.right          }          return key        }          //寻找最小值        BinarySearchTree.prototype.min = function(){           //1.获取根节点           let node = this.root          //2.定义key保存节点值          let key = null          //3.依次向左不断查找，直到节点为null          while (node != null) {            key = node.key            node = node.left          }          return key        }

测试代码：

   //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);        //4.测试最值      console.log(bst.max());      console.log(bst.min());      

测试结果：

3.2.查找特定值

查找二叉搜索树当中的特定值效率也非常高。只需要从根节点开始将需要查找节点的key值与之比较，若node.key < root则向左查找，若node.key > root就向右查找，直到找到或查找到null为止。这里可以使用递归实现，也可以采用循环来实现。

实现代码：

     //查找特定的key        BinarySearchTree.prototype.search = function(key){          //1.获取根节点          let node = this.root            //2.循环搜索key          while(node != null){            if (key < node.key) {              //小于根(父)节点就往左边找              node = node.left              //大于根(父)节点就往右边找            }else if(key > node.key){              node = node.right            }else{              return true            }          }          return false        }

测试代码：

    //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);        //3.测试搜索方法      console.log(bst.search(24));//false      console.log(bst.search(13));//true      console.log(bst.search(2));//false

测试结果：

4.删除数据

实现思路：

第一步：先找到需要删除的节点，若没找到，则不需要删除；

首先定义变量current用于保存需要删除的节点、变量parent用于保存它的父节点、变量isLeftChild保存current是否为parent的左节点，这样方便之后删除节点时改变相关节点的指向。

实现代码：

        //1.1.定义变量          let current = this.root          let parent = null          let isLeftChild = true            //1.2.开始寻找删除的节点          while (current.key != key) {            parent = current            // 小于则往左查找            if (key < current.key) {              isLeftChild = true              current = current.left            } else{              isLeftChild = false              current = current.rigth            }            //找到最后依然没有找到相等的节点            if (current == null) {              return false            }          }          //结束while循环后：current.key = key

第二步：删除找到的指定节点，后分3种情况：

• 删除叶子节点；
• 删除只有一个子节点的节点；
• 删除有两个子节点的节点；

4.1.情况1：没有子节点

没有子节点时也有两种情况：

当该叶子节点为根节点时，如下图所示，此时current == this.root，直接通过：this.root = null，删除根节点。

当该叶子节点不为根节点时也有两种情况，如下图所示：

若current = 8，可以通过：parent.left = null，删除节点8；

若current = 10，可以通过：parent.right = null，删除节点10；

代码实现：

        //情况1：删除的是叶子节点(没有子节点)          if (current.left == null && current.right ==null) {            if (current == this.root) {              this.root = null            }else if(isLeftChild){              parent.left = null            }else {              parent.right =null            }          }

4.2.情况2：有一个子节点

有六种情况分别是：

当current存在左子节点时（current.right == null）：

• 情况1：current为根节点（current == this.root），如节点11，此时通过：this.root = current.left，删除根节点11；

• 情况2：current为父节点parent的左子节点（isLeftChild == true），如节点5，此时通过：parent.left = current.left，删除节点5；

• 情况3：current为父节点parent的右子节点（isLeftChild == false），如节点9，此时通过：parent.right = current.left，删除节点9；

当current存在右子节点时（current.left = null）：

• 情况4：current为根节点（current == this.root），如节点11，此时通过：this.root = current.right，删除根节点11。

• 情况5：current为父节点parent的左子节点（isLeftChild == true），如节点5，此时通过：parent.left = current.right，删除节点5；

• 情况6：current为父节点parent的右子节点（isLeftChild == false），如节点9，此时通过：parent.right = current.right，删除节点9；

实现代码：

        //情况2：删除的节点有一个子节点          //当current存在左子节点时          else if(current.right == null){              if (current == this.root) {                this.root = current.left              } else if(isLeftChild) {                  parent.left = current.left              } else{                  parent.right = current.left              }          //当current存在右子节点时        } else if(current.left == null){              if (current == this.root) {                this.root = current.rigth              } else if(isLeftChild) {                  parent.left = current.right              } else{                  parent.right = current.right              }        }

4.3.情况3：有两个子节点

这种情况十分复杂，首先依据以下二叉搜索树，讨论这样的问题：

删除节点9

在保证删除节点9后原二叉树仍为二叉搜索树的前提下，有两种方式：

• 方式1：从节点9的左子树中选择一合适的节点替代节点9，可知节点8符合要求；
• 方式2：从节点9的右子树中选择一合适的节点替代节点9，可知节点10符合要求；

删除节点7

在保证删除节点7后原二叉树仍为二叉搜索树的前提下，也有两种方式：

• 方式1：从节点7的左子树中选择一合适的节点替代节点7，可知节点5符合要求；
• 方式2：从节点7的右子树中选择一合适的节点替代节点7，可知节点8符合要求；

删除节点15

在保证删除节点15后原树二叉树仍为二叉搜索树的前提下，同样有两种方式：

• 方式1：从节点15的左子树中选择一合适的节点替代节点15，可知节点14符合要求；
• 方式2：从节点15的右子树中选择一合适的节点替代节点15，可知节点18符合要求；

相信你已经发现其中的规律了！

规律总结：如果要删除的节点有两个子节点，甚至子节点还有子节点，这种情况下需要从要删除节点下面的子节点中找到一个合适的节点，来替换当前的节点。

若用current表示需要删除的节点，则合适的节点指的是：

• current左子树中比current小一点点的节点，即current左子树中的最大值；
• current右子树中比current大一点点的节点，即current右子树中的最小值；

前驱&后继

在二叉搜索树中，这两个特殊的节点有特殊的名字：

• 比current小一点点的节点，称为current节点的前驱。比如下图中的节点5就是节点7的前驱；
• 比current大一点点的节点，称为current节点的后继。比如下图中的节点8就是节点7的后继；

代码实现：

• 查找需要被删除的节点current的后继时，需要在current的右子树中查找最小值，即在current的右子树中一直向左遍历查找；

• 查找前驱时，则需要在current的左子树中查找最大值，即在current的左子树中一直向右遍历查找。

下面只讨论查找current后继的情况，查找前驱的原理相同，这里暂不讨论。

4.4.完整实现

      //删除节点        BinarySearchTree.prototype.remove = function(key){  /*------------------------------1.寻找要删除的节点---------------------------------*/          //1.1.定义变量current保存删除的节点，parent保存它的父节点。isLeftChild保存current是否为parent的左节点          let current = this.root          let parent = null          let isLeftChild = true            //1.2.开始寻找删除的节点          while (current.key != key) {            parent = current            // 小于则往左查找            if (key < current.key) {              isLeftChild = true              current = current.left            } else{              isLeftChild = false              current = current.right            }            //找到最后依然没有找到相等的节点            if (current == null) {              return false            }          }          //结束while循环后：current.key = key    /*------------------------------2.根据对应情况删除节点------------------------------*/          //情况1：删除的是叶子节点(没有子节点)          if (current.left == null && current.right ==null) {            if (current == this.root) {              this.root = null            }else if(isLeftChild){              parent.left = null            }else {              parent.right =null            }          }          //情况2：删除的节点有一个子节点          //当current存在左子节点时          else if(current.right == null){              if (current == this.root) {                this.root = current.left              } else if(isLeftChild) {                  parent.left = current.left              } else{                  parent.right = current.left              }          //当current存在右子节点时        } else if(current.left == null){              if (current == this.root) {                this.root = current.right              } else if(isLeftChild) {                  parent.left = current.right              } else{                  parent.right = current.right              }        }          //情况3：删除的节点有两个子节点          else{            //1.获取后继节点            let successor = this.getSuccessor(current)              //2.判断是否根节点            if (current == this.root) {              this.root = successor            }else if (isLeftChild){              parent.left = successor            }else{              parent.right = successor            }              //3.将后继的左子节点改为被删除节点的左子节点            successor.left = current.left          }        }          //封装查找后继的方法        BinarySearchTree.prototype.getSuccessor = function(delNode){          //1.定义变量,保存找到的后继          let successor = delNode          let current = delNode.right          let successorParent = delNode            //2.循环查找current的右子树节点          while(current != null){            successorParent = successor            successor = current            current = current.left          }            //3.判断寻找到的后继节点是否直接就是删除节点的right节点          if(successor != delNode.right){            successorParent.left = successor.right            successor.right = delNode.right          }          return successor        }

测试代码：

   //测试代码      //1.创建BinarySearchTree      let bst = new BinarySearchTree()        //2.插入数据      bst.insert(11);      bst.insert(7);      bst.insert(15);      bst.insert(5);      bst.insert(3);      bst.insert(9);      bst.insert(8);      bst.insert(10);      bst.insert(13);      bst.insert(12);      bst.insert(14);      bst.insert(20);      bst.insert(18);      bst.insert(25);      bst.insert(6);      bst.insert(19);       //3.测试删除代码      //删除没有子节点的节点      bst.remove(3)      bst.remove(8)      bst.remove(10)        //删除有一个子节点的节点      bst.remove(5)      bst.remove(19)        //删除有两个子节点的节点      bst.remove(9)      bst.remove(7)      bst.remove(15)        //遍历二叉搜索树并输出      let resultString = ""      bst.midOrderTraversal(function(key){        resultString += key + "->"      })      alert(resultString)  

测试结果：

可见三种情况的节点都被成功删除了。

5.二叉搜索树完整封装

    //封装二叉搜索树      function BinarySearchTree(){          //节点内部类        function Node(key){          this.key = key          this.left = null          this.right = null        }          //属性        this.root = null          //方法        //一.插入数据：insert方法:对外向用户暴露的方法        BinarySearchTree.prototype.insert = function(key){          //1.根据key创建节点          let newNode = new Node(key)            //2.判断根节点是否存在          if (this.root == null) {            this.root = newNode            //根节点存在时          }else {            this.insertNode(this.root, newNode)          }        }          //内部使用的insertNode方法:用于比较节点从左边插入还是右边插入        BinarySearchTree.prototype.insertNode = function(node, newNode){          //当newNode.key < node.key向左查找          if(newNode.key < node.key){            //情况1：node无左子节点，直接插入            if (node.left == null) {              node.left = newNode            //情况2：node有左子节点，递归调用insertNode(),直到遇到无左子节点成功插入newNode后，不再符合该情况，也就不再调用insertNode()，递归停止。            }else{              this.insertNode(node.left, newNode)            }          //当newNode.key >= node.key向右查找          }else{            //情况1：node无右子节点，直接插入            if(node.right == null){              node.right = newNode            //情况2：node有右子节点，依然递归调用insertNode(),直到遇到无右子节点成功插入newNode为止            }else{              this.insertNode(node.right, newNode)            }          }        }          //二.树的遍历        //1.先序遍历        //掺入一个handler函数对得到的key进行处理        BinarySearchTree.prototype.preOrderTraversal = function(handler){          this.preOrderTraversalNode(this.root, handler)        }          //封装内部方法，对某个节点进行遍历        BinarySearchTree.prototype.preOrderTraversalNode = function(node,handler){          if (node != null) {            //1.处理经过的节点            handler(node.key)              //2.遍历经过节点的左子节点            this.preOrderTraversalNode(node.left, handler)              //3.遍历经过节点的右子节点            this.preOrderTraversalNode(node.right, handler)          }        }          //2.中序遍历        BinarySearchTree.prototype.midOrderTraversal = function(handler){          this.midOrderTraversalNode(this.root, handler)        }          BinarySearchTree.prototype.midOrderTraversalNode = function(node, handler){          if (node != null) {            //1.遍历左子树中的节点            this.midOrderTraversalNode(node.left, handler)              //2.处理节点            handler(node.key)              //3.遍历右子树中的节点            this.midOrderTraversalNode(node.right, handler)          }        }          //3.后序遍历        BinarySearchTree.prototype.postOrderTraversal = function(handler){          this.postOrderTraversalNode(this.root, handler)        }          BinarySearchTree.prototype.postOrderTraversalNode = function(node, handler){          if (node != null) {            //1.遍历左子树中的节点            this.postOrderTraversalNode(node.left, handler)              //2.遍历右子树中的节点            this.postOrderTraversalNode(node.right, handler)              //3.处理节点            handler(node.key)          }        }          //三.寻找最值        //寻找最大值        BinarySearchTree.prototype.max = function () {          //1.获取根节点          let node = this.root          //2.定义key保存节点值          let key = null          //3.依次向右不断查找，直到节点为null          while (node != null) {            key = node.key            node = node.right          }          return key        }          //寻找最小值        BinarySearchTree.prototype.min = function(){           //1.获取根节点           let node = this.root          //2.定义key保存节点值          let key = null          //3.依次向左不断查找，直到节点为null          while (node != null) {            key = node.key            node = node.left          }          return key        }          //查找特定的key        BinarySearchTree.prototype.search = function(key){          //1.获取根节点          let node = this.root            //2.循环搜索key          while(node != null){            if (key < node.key) {              //小于根(父)节点就往左边找              node = node.left              //大于根(父)节点就往右边找            }else if(key > node.key){              node = node.right            }else{              return true            }          }          return false        }          //四.删除节点        BinarySearchTree.prototype.remove = function(key){  /*------------------------------1.寻找要删除的节点---------------------------------*/          //1.1.定义变量current保存删除的节点，parent保存它的父节点。isLeftChild保存current是否为parent的左节点          let current = this.root          let parent = null          let isLeftChild = true            //1.2.开始寻找删除的节点          while (current.key != key) {            parent = current            // 小于则往左查找            if (key < current.key) {              isLeftChild = true              current = current.left            } else{              isLeftChild = false              current = current.right            }            //找到最后依然没有找到相等的节点            if (current == null) {              return false            }          }          //结束while循环后：current.key = key    /*------------------------------2.根据对应情况删除节点------------------------------*/          //情况1：删除的是叶子节点(没有子节点)          if (current.left == null && current.right ==null) {            if (current == this.root) {              this.root = null            }else if(isLeftChild){              parent.left = null            }else {              parent.right =null            }          }          //情况2：删除的节点有一个子节点          //当current存在左子节点时          else if(current.right == null){              if (current == this.root) {                this.root = current.left              } else if(isLeftChild) {                  parent.left = current.left              } else{                  parent.right = current.left              }          //当current存在右子节点时        } else if(current.left == null){              if (current == this.root) {                this.root = current.right              } else if(isLeftChild) {                  parent.left = current.right              } else{                  parent.right = current.right              }        }          //情况3：删除的节点有两个子节点          else{            //1.获取后继节点            let successor = this.getSuccessor(current)              //2.判断是否根节点            if (current == this.root) {              this.root = successor            }else if (isLeftChild){              parent.left = successor            }else{              parent.right = successor            }              //3.将后继的左子节点改为被删除节点的左子节点            successor.left = current.left          }        }          //封装查找后继的方法        BinarySearchTree.prototype.getSuccessor = function(delNode){          //1.定义变量,保存找到的后继          let successor = delNode          let current = delNode.right          let successorParent = delNode            //2.循环查找current的右子树节点          while(current != null){            successorParent = successor            successor = current            current = current.left          }            //3.判断寻找到的后继节点是否直接就是删除节点的right节点          if(successor != delNode.right){            successorParent.left = successor.right            successor.right = delNode.right          }          return successor        }      }

二、平衡树

二叉搜索树的缺陷：

当插入的数据是有序的数据，就会造成二叉搜索树的深度过大。比如原二叉搜索树右 11 7 15 组成，如下图所示：

当插入一组有序数据：6 5 4 3 2就会变成深度过大的搜索二叉树，会严重影响二叉搜索树的性能。

非平衡树

• 比较好的二叉搜索树，它的数据应该是左右均匀分布的；
• 但是插入连续数据后，二叉搜索树中的数据分布就变得不均匀了，我们称这种树为非平衡树；
• 对于一棵平衡二叉树来说，插入/查找等操作的效率是O（logN）；
• 而对于一棵非平衡二叉树来说，相当于编写了一个链表，查找效率变成了O（N）;

树的平衡性

为了能以较快的时间O（logN）来操作一棵树，我们需要保证树总是平衡的：

• 起码大部分是平衡的，此时的时间复杂度也是接近O（logN）的；
• 这就要求树中每个节点左边的子孙节点的个数，应该尽可能地等于右边的子孙节点的个数；

常见的平衡树

• AVL树：是最早的一种平衡树，它通过在每个节点多存储一个额外的数据来保持树的平衡。由于AVL树是平衡树，所以它的时间复杂度也是O（logN）。但是它的整体效率不如红黑树，开发中比较少用。
• 红黑树：同样通过一些特性来保持树的平衡，时间复杂度也是O（logN）。进行插入/删除等操作时，性能优于AVL树，所以平衡树的应用基本都是红黑树。

参考资料：JavaScript数据结构与算法