论文解读（GATv2）《How Attentive are Graph Attention Networks?》

• 2022 年 8 月 18 日
• 笔记
• 论文解读

论文信息

论文标题：How Attentive are Graph Attention Networks?
论文作者：Shaked Brody, Uri Alon, Eran Yahav
论文来源：2022,ICLR
论文地址：download 
论文代码：download

1 Abstract

　　在 GAT中，每个节点都为它的邻居给出自己的查询表示。然而，在本文中证明了 GAT 计算的是一种非常有限的注意类型：注意力分数在查询节点上是无条件的。本文将其定义为静态注意力，并提出了相应的动态注意力 GATv2。

2 Introduction

3 Preliminaries

3.1 Graph neural networks

　　　　$\boldsymbol{h}_{i}^{\prime}=f_{\theta}\left(\boldsymbol{h}_{i}, \text { AGGREGATE }\left(\left\{\boldsymbol{h}_{j} \mid j \in \mathcal{N}_{i}\right\}\right)\right)  \quad\quad\quad(1)$

3.2 Graph attention networks

　　　　$e\left(\boldsymbol{h}_{i}, \boldsymbol{h}_{j}\right)=\text { LeakyReLU }\left(\boldsymbol{a}^{\top} \cdot\left[\boldsymbol{W} \boldsymbol{h}_{i} \| \boldsymbol{W} \boldsymbol{h}_{j}\right]\right)\quad\quad\quad(2)$

　　注意函数的定义为：

　　然后，GAT计算相邻节点的变换特征的加权平均值（然后是一个非线性 $\sigma$）作为 $i$ 的新表示，使用归一化注意系数：

　　　　$\boldsymbol{h}_{i}^{\prime}=\sigma\left(\sum\limits _{j \in \mathcal{N}_{i}} \alpha_{i j} \cdot \boldsymbol{W} \boldsymbol{h}_{j}\right)\quad\quad\quad(4)$

4 The expressive power of graph attention mechanisms

4.1 The importance of dynamic weighting

　　给定一个查询向量，如果注意力函数总是对一个键的权重至少和任何其他键一样大，而无需进行查询，就说这个注意函数是静态的：

　　Definition 3.1 (Static attention). A (possibly infinite) family of scoring functions $\mathcal{F} \subseteq \left(\mathbb{R}^{d} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\right)$ computes static scoring for a given set of key vectors $\mathbb{K}=\left\{\boldsymbol{k}_{1}, \ldots, \boldsymbol{k}_{n}\right\} \subset \mathbb{R}^{d}$ and query vectors $\mathbb{Q}=\left\{\boldsymbol{q}_{1}, \ldots, \boldsymbol{q}_{m}\right\} \subset \mathbb{R}^{d}$ , if for every $f \in \mathcal{F}$ there exists a “highest scoring” key $j_{f} \in[n]$ such that for every query $i \in[m]$ and key $ j \in[n]$ it holds that $f\left(\boldsymbol{q}_{i}, \boldsymbol{k}_{j_{f}}\right) \geq f\left(\boldsymbol{q}_{i}, \boldsymbol{k}_{j}\right)$ . We say that a family of attention functions computes static attention given $\mathbb{K}$ and $\mathbb{Q}$ , if its scoring function computes static scoring, possibly followed by monotonic normalization such as softmax.

　　对动态注意力机制的定义：

　　Definition  3.2  (Dynamic attention). A (possibly infinite) family of scoring functions  $\mathcal{F} \subseteq   \left(\mathbb{R}^{d} \times \mathbb{R}^{d} \rightarrow \mathbb{R}\right)$  computes dynamic scoring for a given set of key vectors  $\mathbb{K}=\left\{\boldsymbol{k}_{1}, \ldots, \boldsymbol{k}_{n}\right\} \subset \mathbb{R}^{d}$  and query vectors  $\mathbb{Q}=\left\{\boldsymbol{q}_{1}, \ldots, \boldsymbol{q}_{m}\right\} \subset \mathbb{R}^{d}$ , if for any mapping  $\varphi:[m] \rightarrow[n]$  there exists  $f \in \mathcal{F}$  such that for any query  $i \in[m]$  and any key  $j_{\neq \varphi(i)} \in[n]: f\left(\boldsymbol{q}_{i}, \boldsymbol{k}_{\varphi(i)}\right)>f\left(\boldsymbol{q}_{i}, \boldsymbol{k}_{j}\right)$ . We say that a family of attention functions computes dynamic attention for  $\mathbb{K}$  and  $\mathbb{Q}$ , if its scoring function computes dynamic scoring, possibly followed by monotonic normalization such as softmax.

　　提高注意力系数的方法可以考虑衰减其他 key 的注意力权重，不一定得增加自身所关心的 key 注意力权重。

4.2 The limited expressivity of GAT

　　Theorem 1. A GAT layer computes only static attention, for any set of node representations  $\mathbb{K}=   \mathbb{Q}=\left\{\boldsymbol{h}_{1}, \ldots, \boldsymbol{h}_{n}\right\}$ . In particular, for  $n>1$ , a GAT layer does not compute dynamic attention.

　　证明：

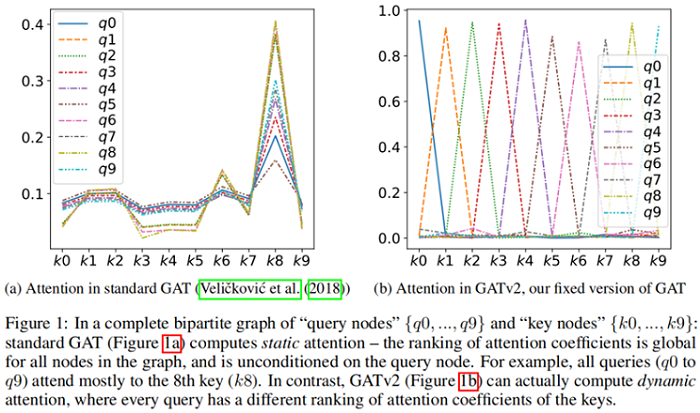
　　Theorem 1 的结果是，节点集 $\mathcal{V}$ 中存在一个 $s_{j}=\boldsymbol{a}_{2}^{\top} \boldsymbol{W} \boldsymbol{h}_{j}$ 使得 节点 $j$ 的全局排名最高，那么造成的结果就是 节点 $j$ 的局部领域 $\mathcal{N}_{i}$ 排名也最高。$\boldsymbol{h}_{i}$ 的唯一影响是在所产生的注意力分布的 “sharpness” 上。这在 Figure 1a（bottom）中得到了演示，其中不同的曲线表示不同的 query $\left(\boldsymbol{h}_{i}\right)$。

　　对于多头注意力机制，Theorem 1 同样适用于每个头。

4.3 Building dynamic graph attention networks

　　standard GAT 评分函数（$\text{Eq.2}$）的主要问题是学习到的 $\boldsymbol{W}$ 和 $\boldsymbol{a}$ 是连续应用的，因此可以分解成一个单一的线性层。为了解决这个限制，我们简单地在非线性之后应用一层(LeakyReLU)，在连接之后应用 $\boldsymbol{W}$，有效地应用一个MLP来计算每个查询键对的分数：

　　GAT ：  $e\left(\boldsymbol{h}_{i}, \boldsymbol{h}_{j}\right)=\mathrm{LeakyReLU}\left(\boldsymbol{a}^{\top} \cdot\left[\boldsymbol{W} \boldsymbol{h}_{i} \| \boldsymbol{W} \boldsymbol{h}_{j}\right]\right)$

Complexity

时间复杂度

　　GAT：$\mathcal{O}\left(|\mathcal{V}| d d^{\prime}+|\mathcal{E}| d^{\prime}\right)$　　

参数复杂度

5 Evaluation

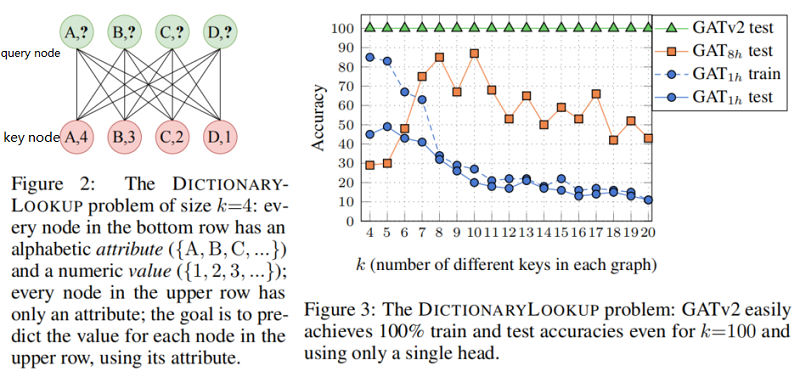
5.1 Synthetic benchmark:DICTIONARYLOOKUP

　　本节在条形码预测问题上验证 GAT v2 的有效性。

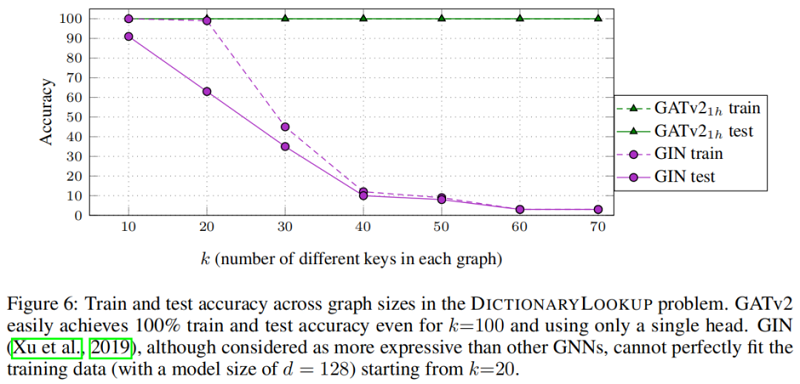
　　对比一下 GIN：

　　同样对于 条形码预测问题 ，其可视化结果如下：

The role of multi-head attention

　　提了一嘴，说多头注意力是稳定学习过程的一种方法，但是呢，你可以想想每对节点对有多个注意力系数是不是很难解释？反正有人吐槽过这一点。

　　下图也有说明了 多头注意力并不是在所有数据集上都有效。

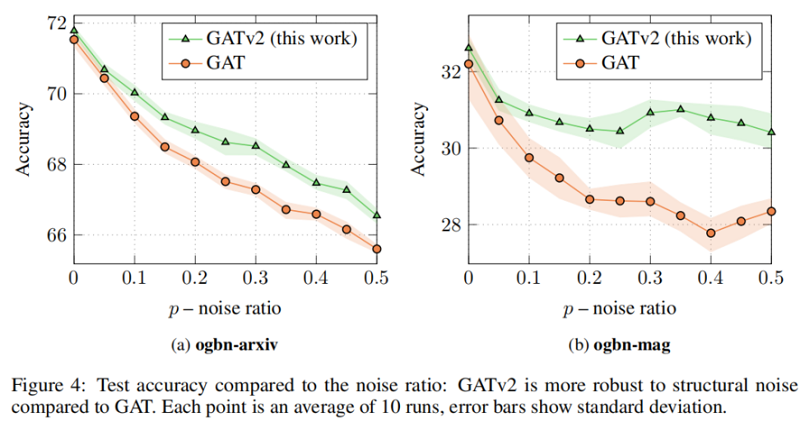
5.2 Robustness to noise

　　我们研究了动态注意和静态对噪声的注意的鲁棒性。特别地，我们关注结构噪声：给定一个输入图 $\mathcal{G}=(\mathcal{V}, \mathcal{E})$ 和一个噪声比为 $0 \leq p \leq 1$，我们从 $\mathcal{V} \times \mathcal{V} \backslash \mathcal{E}$ 中随机抽取 $|\mathcal{E}| \times p$ 不存在的边 $\mathcal{E}^{\prime}$。然后，我们在有噪声的图 $\mathcal{G}^{\prime}=\left(\mathcal{V}, \mathcal{E} \cup \mathcal{E}^{\prime}\right)$ 上训练GNN。

5.3 Programs:Varmisuse

　　验证在 Varmisuse 的结果：

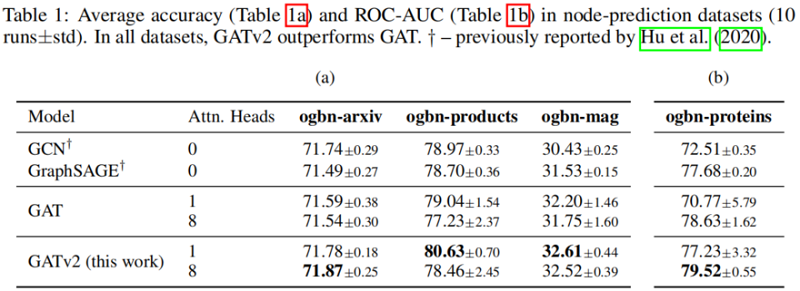
5.4 Node-prediction

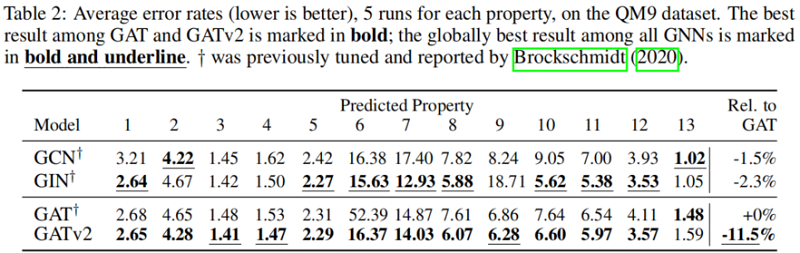
5.5 Graph-prediction:QM9

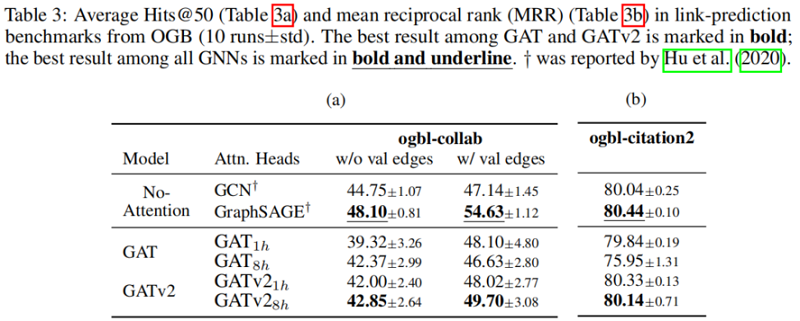
5.6 link-prediction

　　

5.7 Discussion

　　在所有被检查的基准测试中，我们发现 GATv2 比 GAT 更准确。此外，我们发现 GATv2 对噪声的鲁棒性明显高于 GAT。在条形码预测基准测试中，GAT 不能表达数据，因此甚至能达到较差的训练精度。

Which graph attention mechanism should I use?

　　通常不可能预先确定哪种体系结构的性能最好。一个理论上较弱的模型在实践中可能表现得更好，因为如果任务 “easy-to-overfit” 且不需要这样的表达能力，那么一个更强的模型可能会过度拟合训练数据。直观地说，我们认为节点之间的相互作用越复杂，GNN从理论上更强的图注意机制中获得的好处就越大。主要的问题是问题是否有“有影响力 ”节点的全局排名(GAT就足够了)，或者不同的节点有不同的邻居排名(使用GATv2)。

　　GAT的作者在 Twitter 上证实，GAT 被设计用于当时的 “容易过拟合” 的数据集，如 Cora，Citeseer 和 Pubmed，在那里，数据可能有一个 “globally important” 节点的潜在静态排名。更新和更具挑战性的基准测试可能需要更强的注意机制，如GATv2。在本文中，我们回顾了传统的假设，并表明许多现代图基准和数据集包含更复杂的交互，因此需要动态的关注。

6 Conclusion

 　　在本文中，我们发现流行和广泛使用的图注意网络不计算动态注意。相反，GAT的标准定义和实现中的注意机制只是静态的：对于任何查询，它的邻居评分对于每个节点的分数都是单调的。因此，GAT甚至不能表达简单的对齐问题。为了解决这一限制，我们引入了一个简单的修复并提出了GATv2：通过修改GAT中的操作顺序，GATv2实现了一个通用的近似注意函数，因此严格比GAT更强大。

　　我们在一个需要动态选择节点的综合问题中，展示了GATv2相对于GAT的经验优势，以及来自OGB和其他公共数据集的11个基准测试。我们的实验表明，在具有相同参数成本的情况下，GATv2在所有基准测试中都优于GAT。