【干货】一份小白前端可视化学习指南——附思维导图

前言

因为群里粉丝一直要求我写一篇可视化入门指南，今天他来了。其实说起前端可视化，大家所能想到的就是各种图表，大屏。这种看着贼炫酷，而笔者呢工作也一直从事3D前端开发工作，慢慢对图形产生了兴趣。但是呢一直做的是三维的东西，没搞过二维的。大概是2月前开始学习2D的一些东西，然后并写了一些文章，效果还不错。所以我就写一些经验之谈，大佬勿喷。 我大概从4个方面去讲我是怎么学习的

  1. 可视化不得不掌握的数学基础

  2. svg方面的学习

  3. canvas方面的学习

  4. 可视化中不得不掌握的图形算法

读完本篇文章，你可以大概知道我该怎么去学，需要学什么？以及我推荐的一些学习资料和学习资源！

数学篇

提起数学很多程序员头疼哇，我写代码还要学可恶的数学，但是我很明确的告诉你——很重要，如果你想学可可视化的话，数学很重要，背后的几何意义更重要。读者一开始理解不深，导致很多东西理解不了，吃了很多亏哇！

向量

在二维空间或者三维空间中， 是不是都有点的概念，只不过一个是二维的一个是三维的， 假设，现在这个平面直角坐标系上有一个向量 v。向量 v 有两个含义：一是可以表示该坐标系下位于 (x, y) 处的一个点；二是可以表示从原点 (0,0) 到坐标 (x,y) 的一根线段。

向量

我在写canvas的同时就喜欢用一个Point2d 类就是这个原理， canvas本身就是坐标系。画布上的点都可以用向量表示， 原点在左上方。

向量加减法

一个向量可以用其他两个向量去表示，也可以用两个向量去做减法，我说个实际工作中经常用到的例子： 如何让一个点在某一个方向延展多少长度呢？

这里其实就是用到了向量的加法， 首先这个方向肯定是是个单位向量 ， 为什么是单位向量呢？？ 因为向量是有大小和方向的， 而单位向量 只有方向， 长度 为1 ，然后我们只要开始点 加上 这个方向向量 ✖️ 长度。就可以得到了。 背后不就是向量加法的运用。 我还是画图给大家展示下吧。

向量加法

如图：我要从A-B点 方向是od 然后你可以乘以任何长度 得到 OD 然后相加， 是不是就可以得到B点了。 一图胜千言！，减法大家可以自己去思考，同样的道理的

向量的叉乘和点乘

其实很多种实践，这里我就举一个例子哈，带你了解点乘。其实还有投影

向量点乘可以用来判断 连个向量是否同一方向， 我还是画图给大家讲解， 不说太多理论，都是实战中经常用到的。

叉乘

A向量和B向量之间的夹角是锐角 所以是同向 ， B向量和C量之间的夹角是钝角所以是反向 ，因为点乘的数学公式就是两个向量的模长 × cosθ 。

叉乘

叉乘的几何意义也是非常重要的，可以算多边形的面积， 计算出另一个向量 垂直于这两个向量。 还是开始画图：

垂直

X向量 和 Y向量去做叉乘 得到的 向量Z 是 xy 平面的normal。

算面积：

面积

叉乘的数学意义： A向量的模长 × B向量的模长 × sinθ 不就是平行四边形的高 H 所以可以用来算面积。

叉乘还可以用来判断三个点的方向

Corss 的几何叉积得到的是一个数值， 只要判断当前数值是大于0 小于 0就好了， 就知道这个三个点的方式是逆时针 还是顺时针就好了。

顺时针还是逆时针

图中可以看到 OAB 和OA1B 的方向是不同，OA向量✖️ OB向量 的值 和 OA1 ✖️OB向量 算出的来的值 是相反的。公式我给大家列举下：

a.x * b.y – a.y * b.x

其实向量的点乘 和叉乘非常的重要，大家一定要要好理解，后面的图形算法，很多也是基于这个去实现的。

矩阵

空间中图形的大部分变化都是可以通过矩阵去表示的，大概有下面几种类型：

  1. 平移矩阵
  2. 旋转矩阵
  3. 缩放矩阵
  4. 镜像矩阵
  5. 错切矩阵
  6. 投影矩阵

这里我给大家推荐的学习资源是B站的：

//www.bilibili.com/video/BV1ib411t7YR?from=search&seid=15308763710996235630

线性代数的本质，看完你就能够明白了，包括上面的向量之间的变化。

镜像矩阵我推荐你看我这篇文章， 我是求导了三维空间中任意平面的镜像矩阵的了，

求空间任意平面的镜像矩阵

我这里给大家简单的讲解下最简单的变化—— 平移矩阵

还是看下图吧:

平移矩阵

在这样的三维坐标系中从A点平移到B点 x变化了 2 y变化了0 z 变化了 2 对应矩阵的写法是什么呢：
$$
\begin{bmatrix}
1&0&0&2\
0&1&0&0\
0&0&1&2\
0&0&0&1\
\end{bmatrix}
×
\begin{bmatrix}
2\
0\
4\
1\
\end{bmatrix}

=

\begin{bmatrix}
4\
0\
6\
1\
\end{bmatrix}
$$

其实矩阵中每一行都有对应的矩阵， 平移矩阵一般改变的第四列的前三个数字

曲线

无论是2d还是3d都需要曲线的表达，最简单的圆弧、椭圆弧、然后连续曲线可以用贝塞尔曲线去表达，还有B样条曲线，nurbs曲线。掌握曲线最终的还是数学哇。

圆的方程： x ^2 + y ^ 2 = r ^ 2

椭圆的方程： x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1

n阶贝塞尔曲线的方程： 𝐵(𝑡)=∑𝑖=0𝑛𝑃𝑖(1−𝑡)𝑛−𝑖𝑡𝑖,𝑡𝜖[0,1]

b样条曲线和nurbs曲线我还没接触过，但是我们组的小伙伴正在做自由曲面，可能涉及到了。这里我只是简单表示了直线方程，有了方程你可以你去进行高度模拟，比如我在做3D文字的时候，我们底层算法库还没有支持贝塞尔， 不过没关系我们不是有方程嘛， 可以通过方程将贝塞尔曲线离散成多个点，然后用直线去表达。因为我们人眼去看屏幕上的东西，离散的很多的话，肉眼是完全看不出来的。 我这里给大家看一张图吧：

弧线

圗这个部分的弧线我就是用我贝塞尔曲线 离散成直线去表达的， 还有国中的点其实也是贝塞尔曲线离散成直线去做的。从视觉上来看是能够近似模拟的。3D文字中的 更多技术，我后面会专门写一篇文章去详细介绍， 顺便自己去梳理下。如果你感兴趣，那你可得关注我，不然就找不到我了。

坐标系的转换

为什么要有这个东西呢，canvas和svg的坐标系都是左上方是原点，这一点你不觉得有点反人类？ 好不舒服，我在画折线图的时候就发现了，从原点向上，坐标轴是递减的。其实这个问题怎么解决呢，其实很简单就是我们进行坐标系的转换，我将原先画布的原点， 通过变化到左下角， 这样我们在计算点的坐标的时候，就没有心智负担了，该怎样就是怎样。 说完2d我再和你聊聊3D， 就拿Three.js 举例子吧有个局部坐标系，观察坐标系（相机）、 世界坐标系、裁剪坐标系、屏幕坐标系。

这是空间中某个物体到最终屏幕所做的一系列操作。

  1. 首先物体的自身有个坐标系我们叫做局部坐标系，他也有个原点，但是他在世界坐标系下也有对应的位置，所以他们之间有一个矩阵变化——模型矩阵

  2. 世界坐标系——到观察坐标系也有矩阵变化， 这叫视图矩阵

  3. 观察空间——裁剪空间 叫做 投影矩阵因为3维空间的东西我们是用相机去模拟人眼，在视椎体内的东西才能被看到。所有就有了投影矩阵， 有透视投影和正交投影， 一个近大远小，一个远近都是一样的

  4. 标准设备坐标-屏幕坐标。 这里就涉及到坐标系的原点的问题。

    坐标系

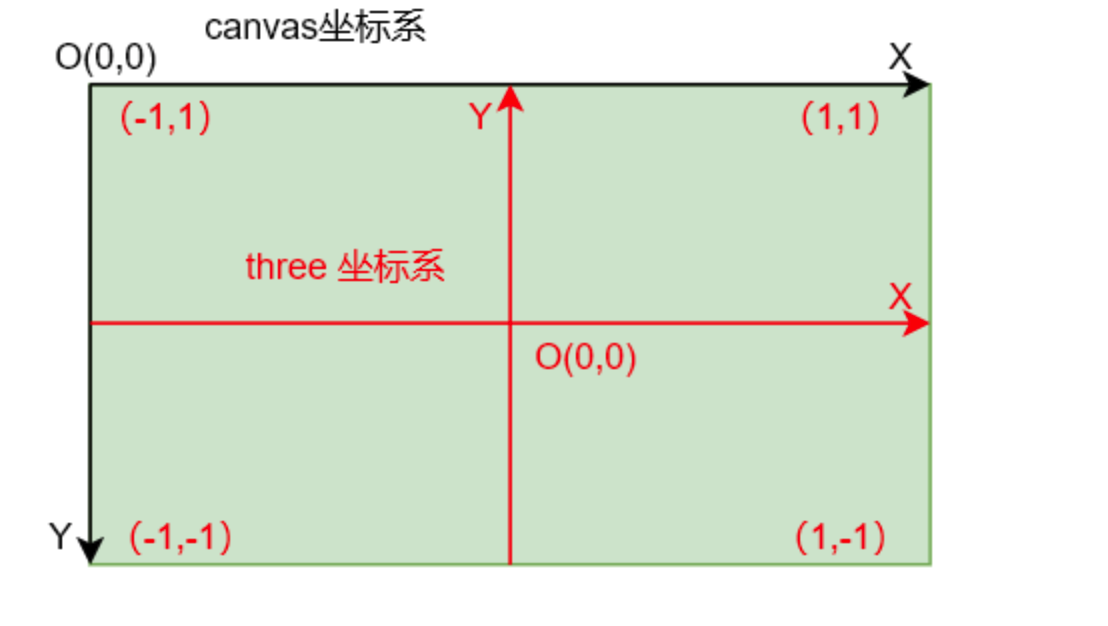
归一化的坐标是相对于画布中心的， 但是canvas默认的坐标系是左上角的。 我们分析下坐标系的变化，首先Y轴是相反的所以 第一个变化就是 X不变，然后Y都✖️ -1这下方向对了，差的就是偏移量。 x轴和Y轴差的偏移量都是画布的一半宽度和高度。 这样就实现了，到屏幕坐标的转换了。

svg和canvas

SVG和canvas的学习我还是推荐Mdn, 大家去认真从头撸一遍，然后再谈进阶，再去如何优化， 你连基本的api都不熟悉和谈进阶对吧。

  1. svg教程 //developer.mozilla.org/zh-CN/docs/Web/SVG/Tutorial

  2. canvas教程 //developer.mozilla.org/zh-CN/docs/Web/API/Canvas_API/Tutorial

    跟着后面学一遍，手敲一遍，自然就明白其中的奥秘。 下面👇是我用了这么久的小经验，和小tips

  3. svg中的path 中大写字母和小写字母的 区别主要是相对定位和绝对定位的关系。

  4. svg的defs标签 不会出现在画布上，是为了下面的组合使用的

  5. svg的g 和 symbols 都可以实现组合 ，但是symbols 有viewbox 也就是视口的概念

  6. use 复用标签 对应上文定义的id

  7. canvas clearRect（） 清除画布 由于canvas 每一帧都要进行重绘

  8. restore() save() 保存当前canvas 的状态 确保不影响 其他绘图元素

  9. isPointinPath（） 可以用来点是不是在最后一个绘制的path 中(有坑) ， 判断点是不是在图形内部最后用算法去解决。

  10. beginPath() 和 closePath() 的使用

  11. 像素级别的处理 imageData 的使用

当你熟悉了这些可以进阶了， 推荐学习

进阶学习

深入理解canvas

//joshondesign.com/p/books/canvasdeepdive/title.html

Canvas 最佳实践（性能优化）

//www.cnblogs.com/mopagunda/p/5622911.html

canvas 离屏渲染

//devnook.github.io/OffscreenCanvasDemo/keep-ui-responsive.html

canvas视频学习

//www.bilibili.com/video/av26151775/

推荐书籍

《HTML5 Canvas核心技术：图形、动画与游戏开发》

《HTML5 2D游戏编程核心技术》

webgl

1.学习图形学基础

一定一定一定要看闫令琪老师的GAMES101现代计算机图形学。建议1.5倍速，大概一个月内可以掌握。跟着课程，把光栅渲染器和光线追踪的作业都做掉，学了这门课，差不多图形学基础就打牢了。对图形学、游戏、3D引擎、OpenGL、Unity、UE差不多也有了基本的认识。我自己还没有看完，还在学习中。

//www.bilibili.com/video/BV1X7411F744?from=search&seid=7915905348717479996

2.webgl 网站学习，这是我觉得质量非常不错同时又有点深度的学习网站

//webglfundamentals.org/webgl/lessons/zh_cn/webgl-fundamentals.html

  1. 着色器和glsl
  2. 光照和颜色
  3. 如何加载外部模型
  4. 点线面如何三角化
  5. 贴图

书籍推荐：

webgl 编程指南

3D游戏与计算机图形学中的数学方法

Fundamentals of Computer Graphics (4th Edition)

directx 9.0 3d游戏开发编程基础 这本书强力推荐 虽然是用c++写的 ，但是他把整个渲染流程讲解的很清楚，我反正看了收获很大。这也是我们老大推荐的一本书。

框架层面

three.js

image-20210808004031389

Three.js 是最知名的 WebGL 项目，Contributions 人数高达 1313，和 React 是一个量级的，尽管它自身的定位只是渲染引擎，但社区硬是把不少游戏引擎的功能都加上了，比如物理引擎、贴花、动画等，在源码中有大量例子，很适合学习，但不少重要功能，比如 gltf 加载器，都是放在 examples 目录里，让人感觉很不正式。

由于知名度最高，Three.js 最大的优势就是社区强大，搜索问题能找到很多答案，也有非常多开源和商业项目使用

但 Three.js 在版本管理方面很不专业，到现在都还没采用 semver 版本命名规范，每次发布都是一个叫 rXXX 的版本，我见过不少基于 Three.js 的项目都是固定在某个版本不敢升级了

babylonjs

image-20210808000356624

最后压轴的是 Babylon，它也是 Sugar 最终采用的 WebGL 引擎，不仅功能强大，代码质量也很高，TypeScript 类型完善，几乎每个函数都有注释。

Babylon 在材质方面功能丰富，除了基础的 PBR，还提供了用于皮肤的次表面渲染 SubSurface、用于车漆的 ClearCoat、用于布料的 Sheen，以及用于光盘之类的各向异性材质 Anisotropy 等等。

Babylon 最后一个亮点是正在开发 WebGPU 版本，而其他引擎都没开始做，所以等 WebGPU 发布后，Babylon 应该是首批支持的，将得到更多关注。

AntV

image-20210808000608074

在AntV中，有好几个不同的可视化引擎，事实上，它们是相互隔绝的，彼此独立的。学习的时候需要单独的去学习。ChartCube图表魔方支持在线的生成图表。地图则使用L7地理空间数据可视化。

echarts

image-20210808000817240

ECharts最初是”Enterprise Charts”（企业图表）的简称，来自百度EFE数据可视化团队，是用JavaScript实现的开源可视化库。ECharts的功能非常强大，对移动端进行了细致的优化，适配微信小程序，支持多种渲染方式和千万数据的前端展现，甚至实现了无障碍访问。底层是用的z-render 这个库去进行封装的。还是很值的学习对的，有点类似于组件的概念，进行可配置的去展示图表。

d3

image-20210808001245616

D3是指数据驱动文档(Data-Driven Documents)。D3.js是一个JavaScript库，它可以通过数据来操作文档。D3可以通过使用HTML、SVG和CSS把数据鲜活形象地展现出来。D3严格遵循Web标准，因而可以让你的程序轻松兼容现代主流浏览器并避免对特定框架的依赖。同时，它提供了强大的可视化组件，可以让使用者以数据驱动的方式去操作DOM。被称为可视化版的jquery。

图形算法

最后讲一下不得不掌握的图形算法， 比如很简答的例子。 判断点是不是在任意多边形内部对吧这就是 涉及到算法。

我大概列举下

  1. 判断点是不是在任意闭合polygon中 用射线检测法， 有内部的点，像任意方向发出一天射线计算出交点的个数， 奇数就是内部 偶数就是外部
  2. 判断连续多边形的方向 是顺时针还是逆时针 **求面积的正负 ** 求平面的noraml (慎用) 对于凹多边形是不准的
  3. 二维图形下， 任意图形的相交 推荐两个库 clipper 和turf 洞和外轮廓的概念，自己可以百度了解
  4. 判断一个点 在某个向量的哪一面 上面的三点求方向逆时针还是顺时针
  5. 线段求线段求相交 直线方程求焦点
  6. 求任意两个区域的包含关系 内部 外部 相交
  7. 碰撞检测 boundingbox 求交集

这里我大概列了一下我工作中用到的一些算法。

推荐一些文章：

谈”求线段交点”的几种算法(js实现,完整版)

//www.cnblogs.com/i-gps/archive/2012/06/19/2554992.html

计算几何与图形学有关的几种常用算法

//blog.csdn.net/wilson1068/article/details/44133303

点在多边形内算法——判断一个点是否在一个复杂多边形的内部

//blog.csdn.net/hjh2005/article/details/9246967

实现多边形的交并差还有偏移

//turfjs.org/

Clipper库中文文档详解

//www.cnblogs.com/zhigu/p/11943118.html

总结

本篇文章大概就是我的个人理解哈，水平有限，能表达的就这么多。如果有更好的欢迎补充学习和交流，文章有错误的欢迎指正。最后送给大家一张思维导图，对照学习哈。我是热爱图形的Fly，我们下次再见👋啦。

思维导图

资源获得

关注公众号【前端图形】，回复 思维导图 二字 可以免费获得高清思维导图 ，以及可视化学习视频 加文中部分书籍📚pdf版本

Tags:

VirMach 便宜 VPS

QNews

QNews