洛谷 P6362 平面欧几里得最小生成树

2021 年 2 月 1 日
笔记
数据结构, 最小生成树

题目描述

平面上有 \(n\) 个点，第 \(i\) 个点坐标为 \((x_i, y_i)\)。连接 \(i, j\) 两点的边权为 \(\sqrt{(x_i – x_j) ^ 2 + (y_i – y_j) ^ 2}\)。求最小生成树的边权之和。

输入格式

第一行一个整数 \(n\)。

接下来 \(n\) 行，每行输入两个整数 \(x_i, y_i\)。

输出格式

输出一行一个实数，表示答案。

当你的答案与标准输出的绝对误差或相对误差在 \(10^{-6}\) 内时，就会被视为正确。

输入输出样例

输入 #1

输出 #1

6.472136

说明/提示

样例解释 1

该样例中，最小生成树如下图所示：

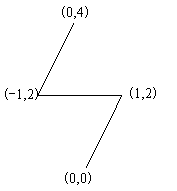
边权之和为 \(2 \sqrt{5} + 2 \approx 6.47213595500\)

数据规模与约定

对于 \(50\%\) 的数据，\(n \le 5000\)。

对于 \(100\%\) 的数据，\(3 \le n \le 10 ^ 5\)，\(\lvert x_i \rvert, \lvert y_i \rvert \le 10 ^ 5\)。

分析

边数太多，肯定不能用 \(Kruskal\)

\(n^2\) 的 \(Prim\) 也过不去

所以可以用 \(Boruvka\) 算法

找到某一个点距离最近的点用 \(kdtree\) 查询就行了

查询的时候加一个剪枝，初始的答案不要置为无穷大，要设为当前联通块内的最优解

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define rg register
inline int read(){
	rg int x=0,fh=1;
	rg char ch=getchar();
	while(ch<'0' || ch>'9'){
		if(ch=='-') fh=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return x*fh;
}
const int maxn=1e5+5;
int cnt,orz,n,rt,x[maxn],y[maxn];
struct KDT{
	int mn[2],mx[2],d[2],lc,rc,id,col;
	friend bool operator <(const KDT& A,const KDT& B){
		return A.d[orz]<B.d[orz];
	}
}tr[maxn],jl[maxn];
void push_up(rg int da){
	rg int lc=tr[da].lc,rc=tr[da].rc;
	for(rg int i=0;i<2;i++){
		tr[da].mn[i]=tr[da].mx[i]=tr[da].d[i];
		if(lc){
			tr[da].mx[i]=std::max(tr[da].mx[i],tr[lc].mx[i]);
			tr[da].mn[i]=std::min(tr[da].mn[i],tr[lc].mn[i]);
		}
		if(rc){
			tr[da].mx[i]=std::max(tr[da].mx[i],tr[rc].mx[i]);
			tr[da].mn[i]=std::min(tr[da].mn[i],tr[rc].mn[i]);
		}
	}
}
int build(rg int l,rg int r,rg int pl){
	orz=pl;
	rg int mids=(l+r)>>1;
	std::nth_element(jl+l,jl+mids,jl+r);
	tr[mids]=jl[mids];
	if(l<mids) tr[mids].lc=build(l,mids-1,!pl);
	if(mids<r) tr[mids].rc=build(mids+1,r,!pl);
	push_up(mids);
	return mids;
}
long long getdis(rg int ax,rg int ay,rg int bx,rg int by){
	return 1LL*(ax-bx)*(ax-bx)+1LL*(ay-by)*(ay-by);
}
long long sqr(rg int aa){
	return 1LL*aa*aa;
}
long long mindis(rg int da,rg int xx,rg int yy){
	rg long long mans=0;
	mans+=sqr(std::max(0,xx-tr[da].mx[0])+std::max(0,tr[da].mn[0]-xx));
	mans+=sqr(std::max(0,yy-tr[da].mx[1])+std::max(0,tr[da].mn[1]-yy));
	return mans;
}
long long nans=0x3f3f3f3f3f3f3f3f;
int haha=0;
void cx(rg int da,rg int xx,rg int yy,rg int zz){
	if(!da) return;
	rg long long tmp=getdis(xx,yy,tr[da].d[0],tr[da].d[1]);
	if(tr[da].col!=zz && nans>tmp){
		nans=tmp,haha=tr[da].id;
	} 
	tmp=mindis(da,xx,yy);
	if(tmp>=nans) return;
	rg long long tmp1=0x3f3f3f3f3f3f3f3f,tmp2=0x3f3f3f3f3f3f3f3f;
	if(tr[da].lc) tmp1=mindis(tr[da].lc,xx,yy);
	if(tr[da].rc) tmp2=mindis(tr[da].rc,xx,yy);
	if(tmp1<tmp2){
		if(tmp1<=nans) cx(tr[da].lc,xx,yy,zz);
		if(tmp2<=nans) cx(tr[da].rc,xx,yy,zz);
	} else {
		if(tmp2<=nans) cx(tr[da].rc,xx,yy,zz);
		if(tmp1<=nans) cx(tr[da].lc,xx,yy,zz);
	}
}
double ans=0;
int bes[maxn],fa[maxn],tot;
long long bes2[maxn];
int zhao(rg int xx){
	if(xx==fa[xx]) return xx;
	return fa[xx]=zhao(fa[xx]);
}
double getdis2(rg int ax,rg int ay,rg int bx,rg int by){
	return sqrt(1.0*(ax-bx)*(ax-bx)+1.0*(ay-by)*(ay-by));
}
int main(){
	n=read();
	for(rg int i=1;i<=n;i++) jl[i].d[0]=read(),jl[i].d[1]=read(),jl[i].id=jl[i].col=i,x[i]=jl[i].d[0],y[i]=jl[i].d[1];
	for(rg int i=1;i<=n;i++) fa[i]=i;
	rt=build(1,n,0);
	rg int tmp=0;
	while(tot<n-1){
		for(rg int i=1;i<=n;i++) bes[i]=0,bes2[i]=0x3f3f3f3f3f3f3f3f;
		for(rg int i=1;i<=n;i++){
			tmp=zhao(i);
			nans=bes2[tmp],haha=-1;
			cx(rt,x[i],y[i],tmp);
			if(haha==-1) continue;
			if(bes2[tmp]>nans){
				bes2[tmp]=nans;
				bes[tmp]=haha;
			} else if(bes2[tmp]==nans){
				if(bes[tmp]<haha) bes[tmp]=haha;
			}
		}
		for(rg int i=1;i<=n;i++){
			tmp=zhao(i);
			if(bes[tmp] && tmp!=zhao(bes[tmp])){
				fa[tmp]=zhao(bes[tmp]);
				ans+=sqrt((double)bes2[tmp]);
				tot++;
			}
		}
		for(rg int i=1;i<=n;i++){
			tr[i].col=zhao(tr[i].id);
		}
	}
	printf("%.6f\n",ans);
	return 0;
}

Tags: 数据结构最小生成树