堆排序
- 2020 年 12 月 6 日
- 笔记
- data structure & algorithm
引入:
堆排序是一种就地算法,算法最坏时间复杂度为O(nlogn)
算法设计技术:以堆(heap)来加速,优先级队列,ADT
要想知道什么是堆排序,必须先了解堆,下面开始介绍堆:
二叉堆:是一颗完全/完整二叉树
1.结点编号从1开始的堆
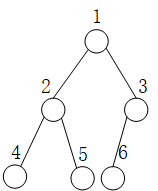
完全二叉树(结点i)

非完全二叉树
父亲 i/2 左孩子 2i 右孩子2i + 1 (比较简洁)
2. 结点编号从0开始
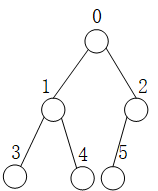
父亲 (i-1)/2 左孩子 2i + 1 右孩子2i + 2 (稍微复杂点)
数组形态 隐式堆
最大堆(大根堆)/最小堆(小根堆)
最大堆(大根堆)
大根堆的特性:
- A[i/2] >= A[i] 最大堆(大根堆)
- i/2为结点i的父亲
- 堆顶/最大元素
- 似乱非乱 完美的混乱
最小堆(小根堆)
小根堆的特性:
- A[i/2] <= A[i] 最小堆(小根堆)
- i/2为结点i的父亲
- 堆顶/最小元素
二叉堆的操作:
- 调整结点i使之满足堆特性O(logn)
- 建堆O(n)
- 堆排序O(nlogn)
- 插入元素O(logn)
- 取出最大元素O(logn)
- 对结点i升权O(logn)
- 最大元O(1)
维护堆特性
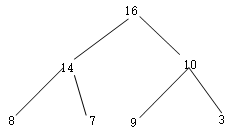
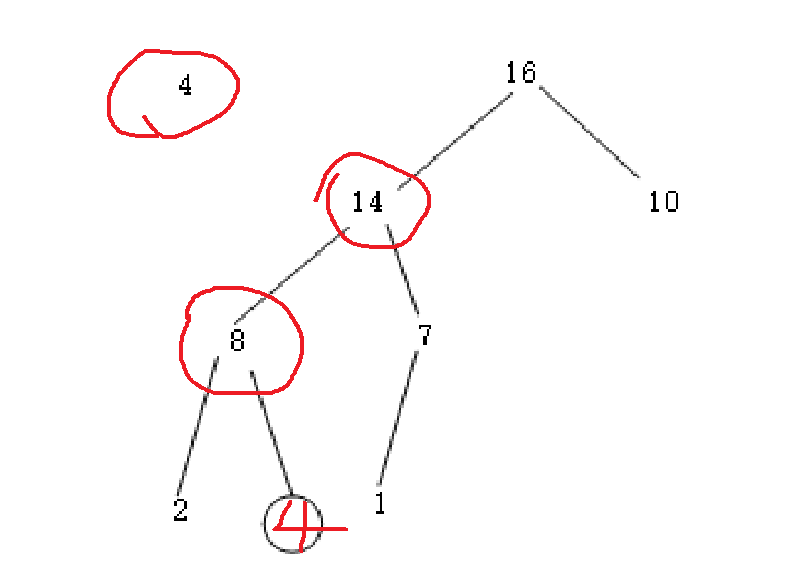
结点i的下沉 其他结点都满足要求(堆的特性)
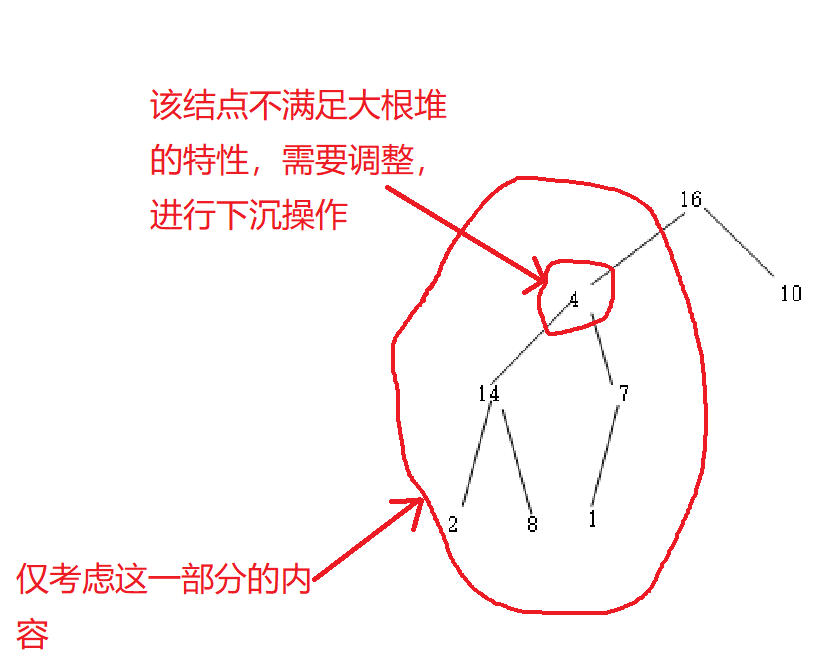
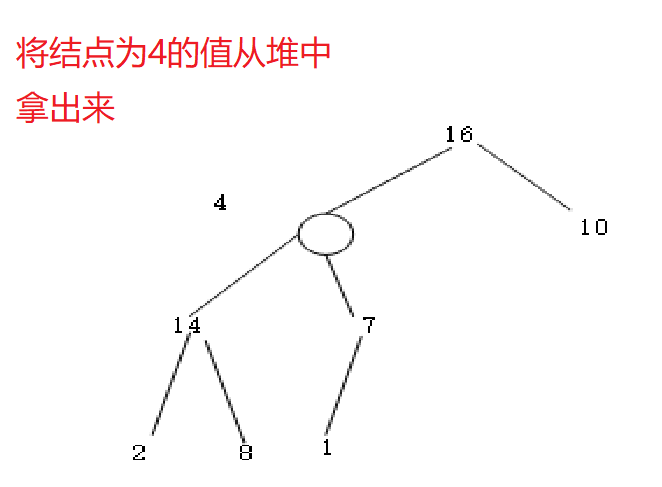
1.将结点为4的值从堆中拿出来
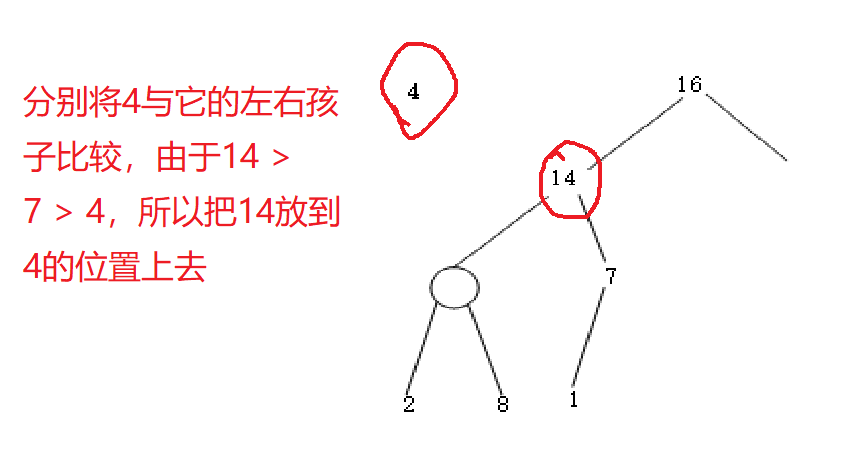
2.分别将4与它的左右孩子比较,由于14 > 7 > 4,所以把14放到4的位置上去
3.继续与原来14位置左右孩子比较,由于8 > 4 > 2,所以把8放到原来14的位置,把4放到原来8的位置
A 数组/向量 n + 1(n个元素) A[0]哨兵


