关于素数定理的证明
了解以下素数定理以及证明
一.质因数分解定理
反证法：假设存在大于1的自然数不能写成质数的乘积，把最小的那个称为n。
自然数可以根据其可除性（是否能表示成两个不是自身的自然数的乘积）分成3类：质数、合数和1。
首先，按照定义，n 大于1。其次，n 不是质数，因为质\数p可以写成质数乘积：p=p，这与假设不相符合。
因此n只能是合数，但每个合数都可以分解成两个严格小于自身而大于1的自然数的积。设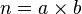
，
其中a 和b 都是介于1和n 之间的自然数，因此，按照n 的定义，a 和b 都都可以写成质数的乘积。
从而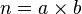 也可以写成质数的乘积。
由此产生矛盾。因此大于1的自然数必可写成质数的乘积。
一.两个相邻的数一定互质
反证法
设相邻两数为：a ,a+1
如果这两数不互质,
必有公约数m
设xm=a ,ym=a+1
有：ym-1=xm 即m(y-x)=1
因为m ,x ,y 都是都是非1正整数
正整数中只有1*1=1
所以m(y-x)不等于1.
证毕
所以a ,a+1这相邻两数必互质.
二.素数是无限的
设n1为素数
则n1与n1+1互质
n1与n1+1至少有两个互不相等的素因数—(1)
如何证明，反证法
外加上，素因数分解定理
n1可以分解成1*一个素数
n1若为素数，易证(1)
n1+1若为合数可以分解成若干个素数的乘积
n1和n1+1的如果有一个相等的素因数m，那么他们的最大公约数就是m
这与n1与n1+1互质（最大公约数是1），相矛盾
n1与n1+1至少有两个互不相等的素因数
设n2=n1*(n1+1)
则n2,与n2+1也至少有两个互不相等的素因数
n3=n2*(n2+1)
则n2,与n2+1也至少有两个互不相等的素因数
则对于nk也成立
所以素数是无限的
证毕
