聊一聊那些線性時間複雜度的排序算法
- 2020 年 4 月 7 日
- 筆記
實際上,基於比較和交換的排序算法,它們的時間複雜度的下限就是O(nlog2n)。冒泡排序,插入排序等自不必多說,時間複雜度是O(n2),即使強如快速排序,堆排序等也只是達到了O(nlog2n)的複雜度。那麼那些傳說中可以突破O(nlog2n)下限,達到線性時間複雜度O(n)的排序算法到底是什麼樣的呢,接下來讓我們一探究竟。
桶排序
基本思想
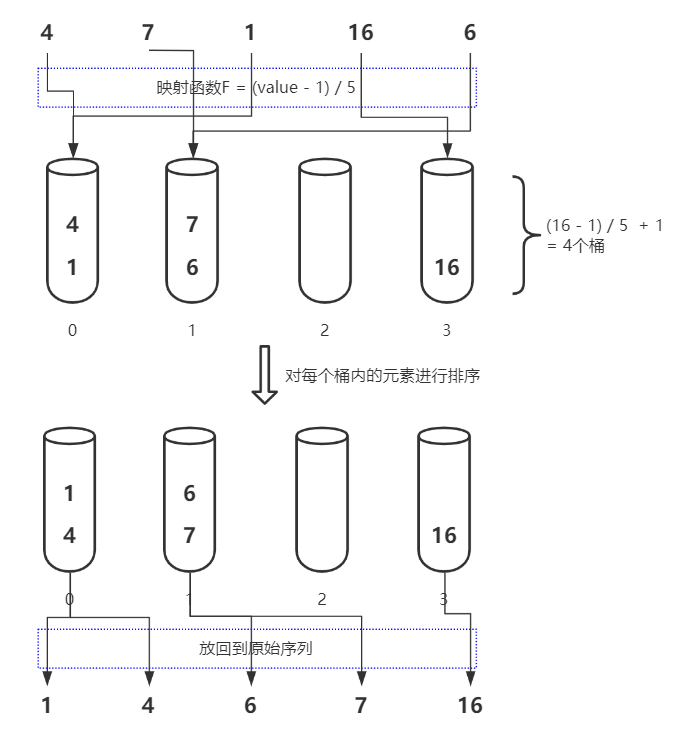
一句話概括就是,將待排序列中的每一個元素通過設定好的映射函數分配到有限數量的桶中,然後再對每個桶中的元素排序。
基本步驟如下:
- 準備有限數量的空桶
- 遍歷待排序列,將每個元素通過映射函數分配到對應的桶中
- 對每個不是空的桶進行排序
- 從每個不是空的桶中再依次把元素放回到原來的序列中
桶排序是利用函數的映射完成了元素的劃分,省略了比較交換的步驟,然後再對桶中的少量數據進行排序,這裡的排序可以根據實際需求選擇任意的排序算法,比如使用快速排序。需要注意的是映射函數的選擇必須保證每個桶是有序的,即一個桶中的所有元素必須大於或小於另一個桶中的所有元素。這樣才能在依次從每個桶中將元素放回到原始序列中時,保證元素的有序性。
複雜度與穩定性與優缺點
-
空間複雜度:O(m + n),m表示桶的數量,n表示需要長度為n的輔助空間
-
時間複雜度:O(n)
桶排序的耗時主要是兩個部分:- 將待排序列的所有元素映射到桶中,時間複雜度O(n)
- 對每個桶內元素排序,因為是基於比較的算法,平均時間複雜度只能達到O(Nilog2Ni),Ni表示每個桶內的元素個數
對於N個元素的待排序列,M個桶,平均每個桶N/M個元素,其桶排序平均時間複雜度可以表示如下:
O(n) + O(M * (N/M)log2(N/M)),當M == N時,複雜度為O(n) -
最好情況:O(n),當待排序列的元素是被均勻分配到桶中時,是線性時間O(n)。各個桶內的數據越少,排序所用的時間也越少,但相應的空間消耗就會增大。當每個桶內只有一個元素時,即M == N,是桶排序的最好情況,真正的達到O(n)
-
最壞情況:所有元素都被分配到同一個桶中,桶排序退化為普通排序。
-
穩定性:穩定
-
優點:穩定,突破了基於比較排序的下限
-
缺點:需要額外的輔助空間,需要好的映射函數
算法實現
public void BucketSort(int[] array){ int max = array[0], min = array[0]; for(int i = 1; i < array.Length; i ++){ if(array[i] > max) max = array[i]; if(array[i] < min) min = array[i]; } List<int>[] buckets = new List<int>[Fun(max, min, array.Length) + 1]; for(int i = 0; i < buckets.Length; i ++){ buckets[i] = new List<int>(); } for(int i = 0; i < array.Length; i ++){ buckets[Fun(array[i], min, array.Length)].Add(array[i]); } int index = 0; for(int i = 0; i < buckets.Length; i ++){ // 桶內的排序藉助了Sort方法,也可以使用其他排序方法 buckets[i].Sort(); foreach(int item in buckets[i]){ array[index ++] = item; } } } // 映射函數,可以根據實際需求選擇不同的映射函數 public int Fun(int value, int minValue, int length){ return (value - minValue) / length; } 【算法解讀】
算法首先確定映射函數Fun,函數的返回值就是元素對應桶的下標。然後找到待排序列中的最大值與最小值,並利用最大最小值確定桶排序需要的桶數量。遍歷待排序列的所有元素並通過映射函數Fun將它們分配到對應下標的桶中。再依次對每個桶內的所有元素進行排序,這裡的使用的是C#提供的Sort方法(也可以選擇不同的排序方法)。當一個桶內的元素排序完畢後再將其放回到原始序列中。
【舉個栗子】
對於待排序列4, 7, 1, 16, 6可以使用下圖表示其桶排序的過程:
計數排序
基本思想
計數排序可以認為是桶排序的一種特殊實現,如果理解了桶排序的話,計數排序就相對很簡單了。
計數排序要求待排序列的所有元素都是範圍都在[0, max]之間的正整數(當然經過變形也可以是負數,比如通過加上某個值,使所有元素都變為正數)
基本步驟如下:
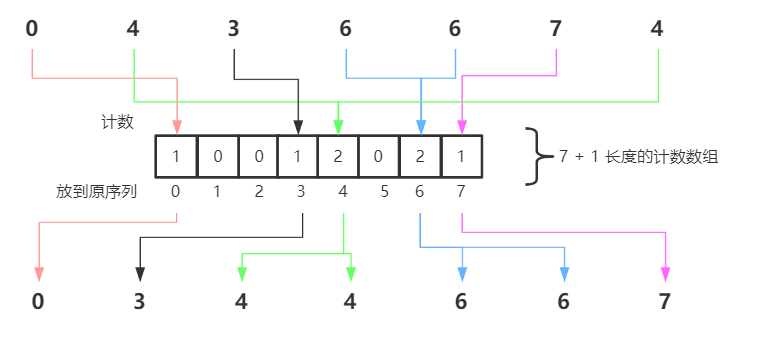
- 得到待排序列中的最大值,構建(最大值 + 1)的計數數組C,可以認為是(最大值 + 1)個桶,只是桶中存放的不再是元素,而是每個元素出現的次數
- 遍歷待排序列,在計數數組中統計每個元素出現的次數。出現一個元素i,則以該元素值為索引的位置上計數加1,即C[i] ++
- 遍歷計數數組,若C[i] > 0,則表示存在有值為i的元素,依次將存在的元素i賦值到原始序列中
複雜度與穩定性與優缺點
- 空間複雜度:O(k)
這裡說明一下,對於計數排序的空間複雜度,很多網上的文章都標註的是O(n + k),其實這與計數排序具體的實現算法有關,有的算法是將計數排序得到的最終序列添加到了一個輔助序列中,而沒有修改原始序列,所以空間複雜度是O(n + k),而本文的實現算法沒有使用輔助序列,直接修改的原始序列,所以空間複雜度是O(k)。而有些文章不管提供的實現算法如何就直接標註O(n + k)的空間複雜度,顯然很容易誤導讀者。 - 時間複雜度:O(n + k),常數k表示待排序列中最大元素的值
- 最好情況:O(n + k)
- 最壞情況:O(n + k)
- 穩定性:穩定
- 優點:穩定,適用於最大值不是很大的整數序列,在k值較小時突破了基於比較的排序的算法下限
- 缺點:存在前提條件,k值較大時,需要大量額外空間
算法實現
public void CountSort(int[] array){ int max = array[0]; for(int i = 0; i < array.Length; i ++){ if(array[i] > max) max = array[i]; } int[] count = new int[max + 1]; for(int i = 0; i < array.Length; i ++){ count[array[i]] ++; } int index = 0; for(int i = 0; i < count.Length; i ++){ while(count[i] -- > 0){ array[index ++] = i; } } } 【算法解讀】
可以看到算法首先獲得待排序列元素中的最大值,然後構建(最大值+1)長度的計數數組。遍歷待排序列的每個元素,並在計數數組中利用元素值為下標記錄元素的出現次數。然後遍歷計數數組,若對應下標的位置上值大於0(等於幾就表示有幾個元素),則表示存在有元素且其值為下標的大小。將該元素添加到原始序列中。由於下標是從小到大的,所以對應得到的序列也是從小到大排列的。
【舉個栗子】
對於待排序列1, 2, 3, 4, 5可以使用下圖表示其計數排序的過程:
基數排序
基本思想
基數排序也是不進行比較,而是通過「分配」和「收集」兩個過程來實現排序的。
首先設立r個隊列,對列編號分別為0~r-1,r為待排序列中元素的基數(例如10進制數,則r=10),然後按照下面的規則對元素進行分配收集:
- 先按最低有效位的值,把n個元素分配到上述的r個隊列中,然後從小到大將個隊列中的元素依次收集起來
- 再按次低有效位的值把剛收集起來的元素分配到r個隊列中,然後再進行收集
- 重複地進行上述分配和收集,直到最高有效位。(也就是說,如果位數為d,則需要重複進行d次,d由所有元素中最大的一個元素的位數計量,比如如果最大數是963,則d = 3)
為什麼這樣就可以完成排序呢?
以從小到大排序為例,首先當按照最低有效位完成分配和收集後,此時得到的序列,是根據元素最低有效位的值從小到大排列的。
當按照次低有效位進行第二次分配和收集後,得到的序列,是先根據元素的次低有效位的值從小到大排列,然後再根據最低有效位的值從小到大排列。
以此類推,當按照最高有效位進行最後一次分配和收集後,得到的序列,是先根據元素的最高有效位的值從小到大排列,再根據次高有效位排列,。。。,再根據次低有效位,再根據最低有效位。自然就完成了每個元素的從小到大排列。
複雜度與穩定性與優缺點
- 空間複雜度:O(n + r),r表示元素的基數,比如十進制元素,則 r = 10
- 時間複雜度:O(d(n + r))
- 最好情況:O(d(n + r))
- 最壞情況:O(d(n + r))
- 穩定性:穩定
- 優點:穩定,時間複雜度可以突破基於比較的排序法的下限
- 缺點:需要額外的輔助空間
算法實現
public void RadixSort(int[] array){ int max = GetMaxValue(array); int[] buckets = new int[10]; int[] buffer = new int[array.Length]; for(int i = 1; max / i > 0; i = i * 10){ // 統計每個桶中的元素個數 for(int j = 0; j < array.Length; j ++){ buckets[array[j] / i % 10] ++; } // 使每個桶記錄的數表示在buffer數組中的位置 for(int j = 1; j < buckets.Length; j ++){ buckets[j] += buckets[j - 1]; } // 收集,將桶中的數據收集到buffer數組中 for(int j = array.Length - 1; j >= 0; j --){ buffer[-- buckets[array[j] / i % 10]] = array[j]; } for(int j = 0; j < array.Length; j ++){ array[j] = buffer[j]; } // 清空桶 for(int j = 0; j < buckets.Length; j ++){ buckets[j] = 0; } } } // 獲得待排序列中的最大元素 public int GetMaxValue(int[] array){ int max = array[0]; for(int i = 1; i < array.Length; i ++){ if(array[i] > max){ max = array[i]; } } return max; } 【算法解讀】
算法針對的是十進制數,所以r=10
首先獲取到待排序列中的最大元素,然後根據最大元素的位數d進行d趟分配與收集
每一趟的分配與收集過程如下:
根據給定的位數,計算待排序列的每個元素在該位上的值,如果某個元素沒有該位,則用0表示。然後使用長度為10的桶數組記錄它們出現的次數(這裡並沒有直接使用桶記錄對應的元素)。再遍歷一遍桶數組buckets[j] += buckets[j - 1];,使每個桶記錄的數值,表示的就是在指定位數上值等於桶索引的元素在輔助數組buffer中的位置。
然後進行收集工作,根據桶數組中記錄的位置信息,依次將對應的元素收集到buffer數組中。最後清空桶,為下一次分配收集做準備。
【舉個栗子】
對於待排序列9, 40, 123, 56, 7,17可以使用下圖表示其基數排序的過程:

更多
上面算法的源碼都放在了GitHub上,感興趣的同學可以點擊這裡查看
更多算法的總結與代碼實現(不僅僅是排序算法),可以查看GitHub倉庫Algorithm