貝葉斯和樸素貝葉斯是啥
- 2020 年 3 月 30 日
- 筆記
一、貝葉斯
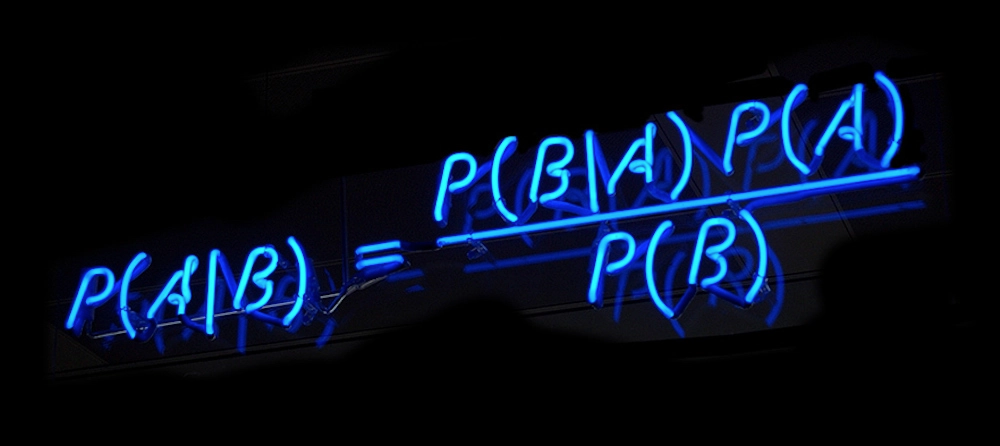
簡單地說,貝葉斯就是你見到貝克漢姆,說了一句yes,研究的是這種概率事件。
開玩笑啦,貝葉斯原理是英國數學家托馬斯·貝葉斯提出的,為了解決一個「逆概率」問題。
例如,如果一個男人發現了他老婆手機里曖昧短訊 ,計算機他老婆出軌的概率。
現實生活中,我們很難知道事情的全貌,當不能準確預知一個事物本質的時候,但是可以依靠和事物本質相關的事件來進行判斷。
先驗概率、似然概率、後驗概率
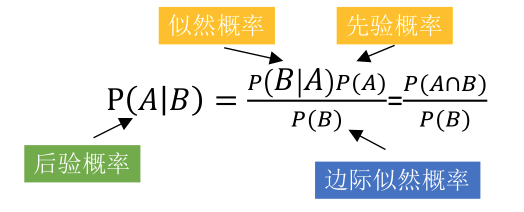
貝葉斯原理類似概率反轉,通過先驗概率和似然概率,推導出後驗概率。
什麼是先驗概率、似然概率、後驗概率?
再以上面出軌的例子為例,
- 先驗概率:男人的老婆沒有任何情況,出軌的概率
- 似然概率:男人的老婆出軌了,手機里有曖昧短訊的概率
- 後驗概率:男人發現老婆手機有曖昧短訊,計算他老婆出軌概率
再舉個例子,產品由不同的工廠ABC生產,每個工廠都有自己的次品率
- 先驗概率:A廠的產品占產品總數的比例
- 似然概率:A廠的次品率
- 後驗概率:已知一件產品是次品,推斷這件產品來自在A廠的概率。(次品可能來自ABC中任意一個廠)
似然概率是由假設正推結果,後驗概率是由結果倒推假設
公式推導

-
(P(A|B)):表示事件B已經發生的前提下,事件A發生的概率,叫做事件B發生下事件A的條件概率。
-
(P(AB)):表示事件A和事件B同時發生的概率
-
(P(AB)=P(BA)),可得(P(AB)=P(BA)=P(B|A)P(A)=P(A|B)P(B))
-
通過(P(A|B))來求(P(B|A)),可得(P(B|A)=frac {P(A|B)P(B)} {P(A)})
-
分母(P(A))可以根據全概率公式分解為:(P(A)=sum_{i=1}^n P(B_i)P(A|B_i))
-
最終公式變為:(P(B|A)=frac {P(A|B)P(B)} {sum_{i=1}^n P(B_i)P(A|B_i)})
二、為什麼需要樸素貝葉斯

假設訓練數據的屬性由n維隨機向量x表示,分類結果用隨機變量y表示,那x和y的統計規律就可以用聯合概率分佈(P(X,Y))描述,每個具體的樣本((x_i,y_i))都可以通過(P(X,Y))獨立同分佈地產生。
貝葉斯分類器的出發點是聯合概率分佈,根據條件概率性質可以得到
(P(X,Y)=P(Y)⋅P(X∣Y)=P(X)⋅P(Y∣X))
- (P(Y)):每個類別出現的概率,先驗概率
- (P(X|Y)):給定的類別下不同屬性出現的概率,似然概率
先驗概率很容易計算出來,只需要統計不同類別樣本的數目即可,而似然概率受屬性數目的影響,估計較為困難。
例如,每個樣本包含100個屬性,每個屬性的取值可能有100種,那分類的每個結果,要計算的條件概率是(100^2=10000),數量量非常龐大。因此,這時候引進了樸素貝葉斯
三、樸素貝葉斯是什麼
樸素貝葉斯,加了個樸素,意思是更簡單的貝葉斯。
樸素貝葉斯假定樣本的不同屬性滿足條件獨立性假設,並在此基礎上應用貝葉斯定理執行分類任務。
簡單地說是
對於給定的待分類項x,分析樣本出現在每個類別中的後驗概率,將後驗概率最大的類作為x所屬的類別
條件獨立

要解決似然概率難以估計的問題,就需要引入條件獨立性假設。
條件獨立性假設保證了所有屬性相互獨立,互不影響,每個屬性獨立地對分類結果發生作用。
這樣條件概率變成了屬性條件概率的乘積
(P(X=x∣Y=c)=)
(P(X(1)=x(1),X(2)=x(2),⋯,X(n)=x(n)∣Y=c))
(prod_{j=1}^nP(X^j=x^j|Y=c))
這是樸素貝葉斯方法,有了訓練數據集,先驗概率(P(Y))和你似然概率(P(X|Y))就可以視為已知條件,用來求解後驗概率(P(X|Y))。
給定的輸入x,樸素貝葉斯分類器利用貝葉斯定理求解後驗概率,並將後驗概率最大的類作為輸出
舉例:長肌肉

肌肉是訓練、睡眠、飲食多種因素組合的結果
| 訓練 | 睡眠 | 飲食 |
|---|---|---|
| 非常好 | 非常好 | 非常好 |
| 好 | 好 | 好 |
| 一般 | 一般 | 一般 |
| 不太好 | 不太好 | 不太好 |
| 不好 | 不好 | 不好 |
| 非常不好 | 非常不好 | 非常不好 |
如果要計算後驗概率,假設屬性不獨立,(6^3)就有了216組合,例如其中是訓練:好,睡眠:不好,包含:一般,這樣的組合複雜度太高了
如條件獨立互不影響後,只需要考慮3個維度的結果,把最終的屬性概率相乘,例如是80%(訓練) * 85%(睡眠) * 90%(飲食),算複雜度降低了幾個數量級。
拉普拉斯平滑

受訓練數據集規模的限制,某個屬性的取值可能在訓練集中從未與某個類同時出現,這就可能導致屬性條件概率為0,些時直接使用樸素貝葉斯分類就會導致錯誤的結論。
例如:在訓練集中沒有樣本同時具有「年齡大於 60」的屬性和「發放貸款」的標籤,那麼當一個退休人員申請貸款時,即使他是李嘉誠,樸素貝葉斯分類器也會因為後驗概率等於零拒絕。
因為訓練集樣本的不充分導致分類錯誤,不是理想的結果,為了避免這種干擾,在計算屬性條件概率時需要添加一個「拉普拉斯平滑」的步驟。
拉普拉斯平滑就是計算類先驗概率和屬性條件概率時,在分子上添加一個較小的修正量,在分母上則添加這個修正量與分類數目的乘積,避免了零概率對分類結果的影響。
半樸素貝葉斯

屬性之間可能具有相關性,而樸素貝葉斯獨立假設性會影響分類性能。
半樸素貝葉斯分類器考慮了部分屬性之間的依賴關係,既保留了屬性之間較強的相關性,又不需要完全計算複雜的聯合概率分佈。
常用方法是建立獨依賴關係:假設每個屬性除了類別之外,最多只依賴一個其他屬性。


