PageRank 算法初步了解
- 2020 年 3 月 16 日
- 筆記
前言
因為想做一下文本自動摘要,文本自動摘要是NLP的重要應用,搜了一下,有一種TextRank的算法,可以做文本自動摘要。其算法思想來源於Google的PageRank,所以先把PageRank給了解一下。
馬爾科夫鏈
我感覺說到PageRank,應該要提起馬爾科夫鏈,因為PageRank在計算的過程中,和馬爾科夫鏈轉移是十分相似的,只是PageRank在馬爾科夫鏈的轉移上做了一些改動。
馬爾科夫鏈的維基百科里是這麼說的:
馬爾可夫鏈是滿足馬爾可夫性質的隨機變量序列(X_{1}, X_{2}, X_{3}, …)。即給出當前狀態,將來狀態和過去狀態是相互獨立的。從形式上看,如果兩邊的條件分佈有定義(即如果(Pr(X_{1}=x_{1},…,X_{n}=x_{n})>0)則(Pr(X_{{n+1}}=xmid X_{1}=x_{1},X_{2}=x_{2},ldots ,X_{n}=x_{n})=Pr(X_{{n+1}}=xmid X_{n}=x_{n}))。
(Xi)的可能值構成的可數集S叫做該鏈的「狀態空間」。
形式定義好像有點複雜。我這裡只想介紹自己所認識的馬氏鏈,一個簡單通俗易懂的馬氏鏈。
假設有一個離散型隨機變量(w),表示的是當前社會中貧窮,中等和富有的人的概率,其初始分佈是:(w=(0.21,0.68,0.11)) 表示社會中貧窮的人佔28%,中等的人佔68%,富有的人佔11%,
這是初始狀態,可以想像成這是我們所處地球的第一代人(X_{1})(那個時候就有貧富差距了),接下來第一代人要生小孩,形成第二代人(X_{2}),這個叫做狀態的轉移,從(X_{1})轉移到(X_{2})。怎麼轉移呢,這是有一個概率的:
| 父代子代 | 兒子是窮人 | 兒子是中等 | 兒子是富人 |
|---|---|---|---|
| 父親是窮人 | 0.65 | 0.28 | 0.07 |
| 父親是中等 | 0.15 | 0.67 | 0.18 |
| 父親是富人 | 0.12 | 0.36 | 0.52 |
上述表格代表的是,父親屬於哪個階級,那兒子屬於某個階級的概率。比如父親是富人,兒子也是富人的概率是 0.52,這表示大概一半的富二代以後都會敗光家產。所以根據以上表格,第二代(X_{2})窮人的概率是 (0.21*0.65+0.68*0.15+0.11*0.12=0.252) 以上的計算過程實際上矩陣相乘,表格里的數據組成一個矩陣(P) 叫做概率轉移矩陣
[ P=begin{bmatrix} 0.65 & 0.28 &0.07 \ 0.15 & 0.67 & 0.18 \ 0.12 & 0.36 & 0.52 end{bmatrix} ]
[ X_{1} cdot P = X_{2} = begin{Bmatrix} 0.252 & 0.554 &0.194 end{Bmatrix} ]
以此類推,不斷計算,不斷狀態轉移,我們發現從第7代開始,就穩定不變了:
[ X_{3} = begin{Bmatrix} 0.270 & 0.512 & 0.218 end{Bmatrix} \ X_{4} = begin{Bmatrix} 0.278 & 0.497 & 0.225 end{Bmatrix} \ X_{5} = begin{Bmatrix} 0.282 & 0.490 & 0.226 end{Bmatrix} \ X_{6} = begin{Bmatrix} 0.285 & 0.489 & 0.225 end{Bmatrix} \ X_{7} = begin{Bmatrix} 0.286 & 0.489 & 0.225 end{Bmatrix} \ X_{8} = begin{Bmatrix} 0.286 & 0.489 & 0.225 end{Bmatrix} \ X_{9} = begin{Bmatrix} 0.286 & 0.489 & 0.225 end{Bmatrix} \ ]
這不是偶然,從任意一個(X_{1})的分佈出發,經過概率轉移矩陣,都會收斂到一個穩定的分佈 (pi=lbrace 0.286,0.489,0.225 rbrace),從(X_{1} rightarrow X_{2} rightarrow X_{3}….rightarrow X_{n}) 這個轉移的鏈條就是馬爾科夫鏈,它最終會收斂到穩定分佈 (pi),也就是 (pi cdot P = pi),至於為什麼會這樣,肯定是和狀態轉移矩陣有關,最終的穩定分佈不是由初始狀態(X_{1})決定的,而是由轉移矩陣(P)決定的,具體就不細究了。
總之,我們得出這樣一個結論,如果有一個隨機變量分佈為(X) 和狀態轉移矩陣(P),隨機變量分佈的下一個狀態(X_{next}) 可以由上一個狀態(X_{pre}) 乘以矩陣(P)得來,那麼經過n步迭代,最終會得到一個不變的,平穩的分佈。
PageRank
PageRank 是谷歌搜索引擎的進行網頁排名算法,它是把所有網頁都構成一張圖,每個網頁是一個節點,如果一個網頁中有鏈向其他網頁的鏈接,那麼就有一條有向邊連接這兩個點。
有了這張圖可以幹嘛嗎?PageRank 認為,每條邊都是一個投票動作,(A rightarrow B) 是A在給B投票,B的權重就會增加。
舉個例子就非常清楚了,假設互聯網上一共就4個頁面,全球幾十億網名,每天只能看這個4個web頁面,這四個頁面分別是A,B,C,D,其中B頁面有兩個超鏈接指向A,C,C中有1個超鏈接指向A,D中有三個超鏈接指向A。其畫成一張圖,就是這樣的:
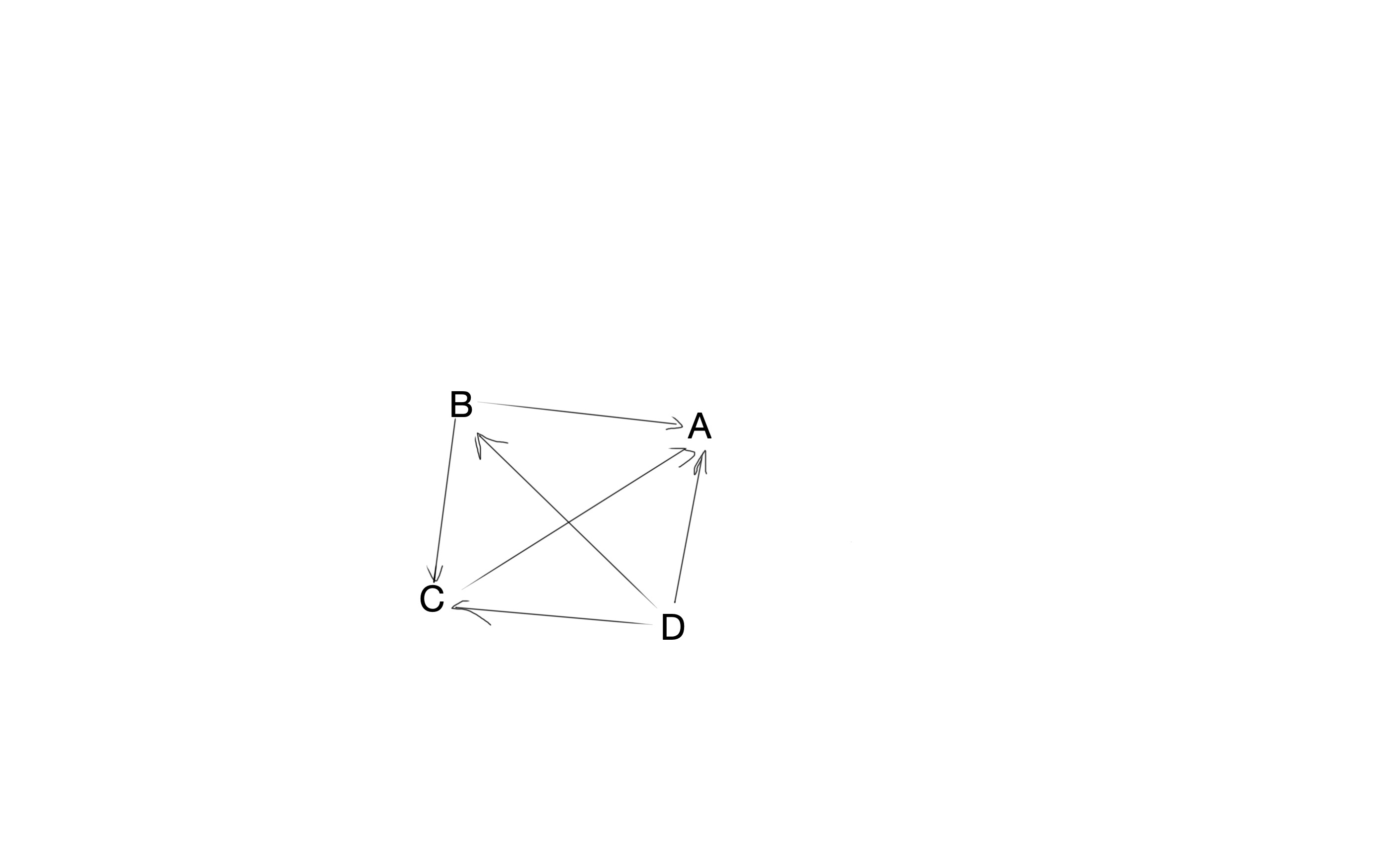
這裡要清楚 PageRank 計算的值是什麼,PageRank 計算的最終值,是每個網頁被往點擊瀏覽的概率,也就相當於權重。所以這還是一個離散型隨機變量,(W=lbrace p_{a},p_{b},p_{c},p_{d} rbrace , p_{a}+p_{b}+p_{c}+p_{d} = 1)。一開始假設每個網頁被瀏覽的概率都是相同的,每個頁面被網民點擊的概率都是0.25,(W=lbrace 0.25,0.25,0.25,0.25 rbrace)
PageRank 的計算過程就和上面所說的馬爾科夫鏈一樣,初始狀態(W_{0})就是全球網民同時上網,每個網民每次都只點擊一次網頁,每個網頁被訪問的概率。那麼狀態2 (W_{1}) 就是全體網民開始點擊瀏覽第二個網頁時,每個網頁被訪問的概率。PageRank 也有一個概率轉移矩陣(P),而(P)就存在於上圖中,其中(P_{i,j}) 表i網頁鏈向j的鏈接數除以i網頁的所有外鏈數。 其實意思就是,當你訪問到i網頁的時候,有多大的概率訪問j網頁。所以對於某個特定的狀態(W_{n}),全體網民開始訪問第n個網頁,它是由上一個狀態(W_{n-1}) 全體網民訪問到第n-1個網頁,通過某種概率得來。這和上面的窮人,富人非常相似。我們計算A頁面在第n次,也就是狀態n的時候被訪問的概率
[ p_{a}^{n} = p_{b}^{n-1} * P_{b,a} + p_{c}^{n-1} * P_{c,a} + p_{d}^{n-1} * P_{d,a} ]
所以
[ W_{1} = W_{0} cdot P,P=begin{Bmatrix} 0.000 & 0.000 & 0.000 & 0.000 \ 0.500 & 0.000 & 0.500 & 0.000 \ 1.000 & 0.000 & 0.000 & 0.000 \ 0.333 & 0.333 & 0.333 & 0.000 end{Bmatrix} ]
整個PageRank 計算直到得到平穩分佈(pi),這就是最終每個網頁被網民點擊的概率,或者叫做權重,排名。
接下來咱們具體計算一下,上述四個頁面A,B,C,D的最終權重是多少。我們寫一段C++ 程序來模擬PageRank 的計算過程。
int main() { int n=4; double d=0.85; double a[4]={0.25,0.25,0.25,0.25}; double b[4][4]={{0,0,0,0},{1,0,1,0},{1,0,0,0},{1,1,1,0}}; double linkNums[4]={0,2,1,3}; printf("轉移矩陣:n"); double p[4][4]; for(int i=0;i<4;i++) { for(int j=0;j<4;j++) { p[i][j] = b[i][j]==0?0:b[i][j]/linkNums[i]; printf("%.3f ",p[i][j]); } printf("n"); } printf("n"); printf("初始狀態:n"); for(int i=0;i<4;i++) { printf("%.3f ",a[i]); } printf("n"); double c[4]; int i=0; int pos=0; while(1) { for(int i=0;i<4;i++) { double x=0; for (int j = 0; j < 4; j++) { x+=a[j]*b[j][i]; } c[i]=x; //c[i]=1.0*(1-d)/n + d*x; } int tag=0; for(int i=0;i<4;i++) { if(a[i] != c[i]) { tag=1; a[i]=c[i]; } } pos++; printf("狀態%d :n",pos); for(int i=0;i<4;i++) { printf("%.3f ",a[i]); } printf("n"); printf("n"); if(tag==0) break; } }其中p是轉移矩陣,a是我們要求的隨機變量的分佈。
運行結果如下
轉移矩陣: 0.000 0.000 0.000 0.000 0.500 0.000 0.500 0.000 1.000 0.000 0.000 0.000 0.333 0.333 0.333 0.000 初始狀態: 0.250 0.250 0.250 0.250 狀態1 : 0.750 0.250 0.500 0.000 狀態2 : 0.750 0.000 0.250 0.000 狀態3 : 0.250 0.000 0.000 0.000 狀態4 : 0.000 0.000 0.000 0.000 狀態5 : 0.000 0.000 0.000 0.000 我們發現,到最後的平穩分佈居然是(lbrace 0,0,0,0 rbrace),為什麼會發生這樣的情況呢?因為D這個網頁,沒有任何網頁鏈接到它,所以在轉移的過程中,它的下一個狀態肯定為0,又因為D變成0了,所以影響到它所鏈接的網頁,最終會導致所有網頁的概率值都變成0。
為了避免這樣的情況,PageRank 引入了一個阻尼係數d和隨機訪問的概念 ,d是一個概率值在0-1之間,這個d的物理意義是當你瀏覽到一個網頁的時候,繼續點擊網頁中的鏈接瀏覽下一個網頁的概率。那麼1-d 表示的就是瀏覽到一個網頁的時候,不通過網頁中的鏈接,而是額外新開了一個窗口隨機訪問其他網頁的概率。所以PageRank 認為訪問網頁,要麼是通過網頁中的鏈接點擊,要麼是隨機訪問。
有了這個阻尼係數d,原先圖中的情況就發生變化了,每個網頁,都有很多條隱形的邊,指向所有其他的網頁,這些隱形的邊表示的是隨機訪問不通過鏈接點擊。因此在計算A頁面在第n次,也就是狀態n的時候被訪問的概率公式就要發生變化了
[ p_{a}^{n} = (p_{b}^{n-1} * P_{b,a} + p_{c}^{n-1} * P_{c,a} + p_{d}^{n-1} * P_{d,a})*d + frac{1-d}{N} ]
物理意義也很好了解,原先從別的網頁通過鏈接點擊過來的是有一定概率的,概率就是d。而從任意一個網頁隨機訪問而來的概率是1/N,還要乘以1-d 。
因此
[ W_{n} = d * W_{n-1} cdot P + frac{1-d}{N} ]
修改一下程序,再運行一下
轉移矩陣: 0.000 0.000 0.000 0.000 0.500 0.000 0.500 0.000 1.000 0.000 0.000 0.000 0.333 0.333 0.333 0.000 初始狀態: 0.250 0.250 0.250 0.250 狀態1 : 0.675 0.250 0.463 0.038 狀態2 : 0.675 0.069 0.282 0.038 狀態3 : 0.368 0.069 0.128 0.038 狀態4 : 0.237 0.069 0.128 0.038 狀態5 : 0.237 0.069 0.128 0.038最終四個網頁的權重再第五步的時候就收斂了,可以看到A網頁的權重是最高的,因為它被指向的鏈接是最多的。
我對 PageRank 算法的初步了解就這麼多了,我覺得PageRank 也應該算是馬爾科夫鏈的應用之一吧。
參考鏈接:
維基百科 :https://zh.wikipedia.org/wiki/PageRank
LDA 數學八卦 PDF: http://bloglxm.oss-cn-beijing.aliyuncs.com/lda-LDA%E6%95%B0%E5%AD%A6%E5%85%AB%E5%8D%A6.pdf


