【小記】二八十十六，進制團團轉

• 2022 年 11 月 4 日
• 筆記
• 學習筆記, 雜項, 計算機基礎

這篇筆記咱主要寫一下二進制、八進制、十進制、十六進制之間的互相轉換。

Contents

• 十進制與其他進制的互相轉換
  • 十進制 → 其他進制
    • 整數部分
      • <方法> 除以基數倒取余
    • 小數部分
      • <方法> 乘以基數順取整
  • 其他進制 → 十進制
    • <方法> 乘以位權後求和
• 二進制與其他進制的互相轉換
  • 二進制 → 其他進制
    • <方法> 幾位一讀，不足補零
  • 其他進制 → 二進制
    • <方法> 展開一位為多位
• 十六進制與八進制的互相轉換
  • <方法> 間接轉換
  • 【例】八進制 → 十六進制
  • 【例】十六進制 → 八進制

前言

通過觀察，我覺得二、八、十、十六進制數的互相轉換可以總結為三大塊：

1. 十進制與其他進制互相轉換
2. 二進制與其他進制互相轉換
3. 十六進制與八進制的互相轉換

話不多說，下面就按這三大塊來歸納一下。

十進制與其他進制的互相轉換

十進制到其他進制

整數部分

💡 方法：除以基數倒取余

比如16進制，除以的基數就是16

1. 「除以基數」指的是將十進制數不斷除以目標進制對應的基數，直到商為0為止。

2. 「倒取余」指的是將每次相除得到的餘數倒序排列，即轉換為了目標進制的數。

   ---

• [例] 10進制轉換為8進制

  

  圖中的紅色箭頭展示了「倒取余」的過程

  圖中將十進制數1145轉換為了八進制數2171

• [例] 10進制轉換為16進制

  

  圖中的紅色箭頭展示了「倒取余」的過程

  圖中將十進制數14191轉換為了十六進制數376F

小數部分

⚠ 不是所有的小數都能轉換為其他進制。比如現代計算機採用二進制計數，有很多小數都沒法準確地轉換為二進制（只能取近似值），這也是為什麼說現在計算機無法完全準確地表示小數。

💡 方法：乘以基數順取整

比如2進制，對應的基數就是2

1. 「乘以基數」指的是不斷將小數部分乘以目標進制對應的基數，直到小數部分為0為止。

2. 「順取整」指的是將每次相乘得到的數的整數部分順序排列，即轉換為了目標進制的數。

   ---

• [例] 2進制轉換為10進制

  

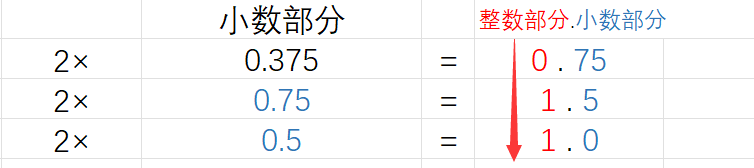
  圖中的紅色箭頭展示了「順取整」的過程

  圖中將十進制數0.375轉換為了二進制數0.011

其他進制到十進制

💡 方法：每一位數字乘上基數^對應指數(位權)，然後相加求和

本圖中的數值12C.1415926，是十六進制數。

上圖中，基數是16，「對應指數」就是橙色標出的數。以小數點為分界，小數點左側第一位的對應指數為0，而小數點右側第一位的對應指數為-1。

從低位向高位（圖中從右向左），這個指數不斷增大。

十六進制的基數是16，那麼八進制的基數就是8，以此類推。

• [例] 16進制轉換為10進制

  

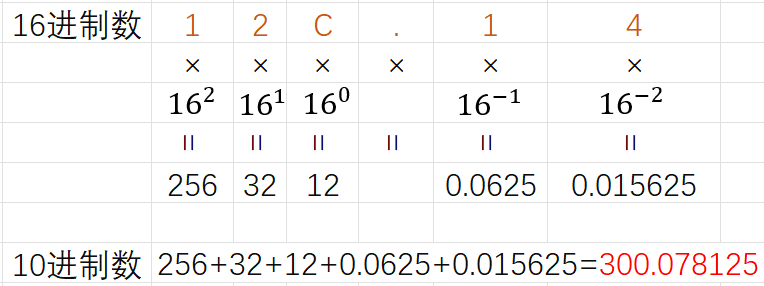
  圖中將十六進制數12C.14轉換為了十進制數300.078125

二進制與其他進制的互相轉換

二進制和其他進制的互相轉換就要方便多了。

二進制到其他進制

💡 方法：以小數點為界，向左右兩側，每幾位讀為一個數，不足的就補零。

• 關於這裡的「每幾位」，需要看要轉換為哪個進制的數。比如轉換為十六進制，其一位能表示0-F這16種狀態，需要用4個二進制位來表示，那麼就是每4位一讀。

  再比如八進制一位能表示0-7這8種狀態，需要用3個二進制位來表示，那麼就是每3位一讀。

• 關於補零，無論是從小數點左側第一位開始往左每幾位一讀，還是從小數點右側第一位開始往右每幾位一讀，都難免遇到「位數不夠讀」的情況，這個時候就需要補零。

  ---

• [例] 二進制轉換為十六進制

  

  圖中將二進制數1001001.011轉換為了十六進制數49.6

  • 紅色箭頭展示了以小數點為分界，分別往左右進行讀取。左側從低位向高位，而右側從高位向低位。
  • 圖中括號展示了補零的過程。100和011都不足4位，按照讀取方向，分別在其左方和右方補零。
  • 最後，每4位一讀，用十六進制表示出來，就得到了最後的結果。

• [例] 二進制轉換為八進制

  

  圖中將二進制數1001101.1011轉換為了八進制數115.54

  • 具體做法和上面一個例子一致，這裡不多贅述。

其他進制到二進制

💡 方法：每位讀為幾位二進制數。

• 關於這裡的「每位讀為幾位二進制數」，需要看轉換前是哪個進制的數。比如原本是十六進制，其一位能表示0-15這16種狀態，需要用4個二進制位來表示，那麼就是每位讀為4位二進制數。

• 附一個對照表：

  八進制位	←對應的二進制	十六進制位	←對應的二進制
  0	000	0	0000
  1	001	1	0001
  2	010	2	0010
  3	011	3	0011
  4	100	4	0100
  5	101	5	0101
  6	110	6	0110
  7	111	7	0111
  –	–	8	1000
  –	–	9	1001
  –	–	A	1010
  –	–	B	1011
  –	–	C	1100
  –	–	D	1101
  –	–	E	1110
  –	–	F	1111

  實際應用中，可以根據8421碼來進行計算，不用死記硬背。

  比如三位二進制101, 對應421，轉換為十進制就是4+1=5。
  再比如四位二進制1010, 對應8421，轉換為十進制就是8+2=10。

  ---

• [例] 八進制轉換為二進制

  

  圖中將八進制數67.23轉換為了二進制數110111.010011

  • 每一位八進制位讀成3位二進制數（一位八進制位能表達8種狀態，需要3位二進制位來表示）

  ---

  不想用8421碼其實也沒問題，八進制和十六進制的每一位數其實可以看作是十進制整數，使用除2倒取余的方法能將其逐位展開為二進制數。
  (本質上還是按位讀取，每位讀為幾位二進制數)

  

  比如上圖中，原八進制數中的6與3分別可以用除2倒取余的方法展開為110與011，和8421碼得出的結果一致。

十六進制與八進制的互相轉換

十六進制和八進制之間無法直接轉換：

• 如果要把十六進制數轉換為八進制數，就需要先將十六進制轉換為十進制或二進制，進而再轉換為八進制。
• 把八進制轉為十六進制也需要用十進制或二進制「過渡一下」

八進制轉十六進制的例子

• 通過二進制進行間接轉換

  

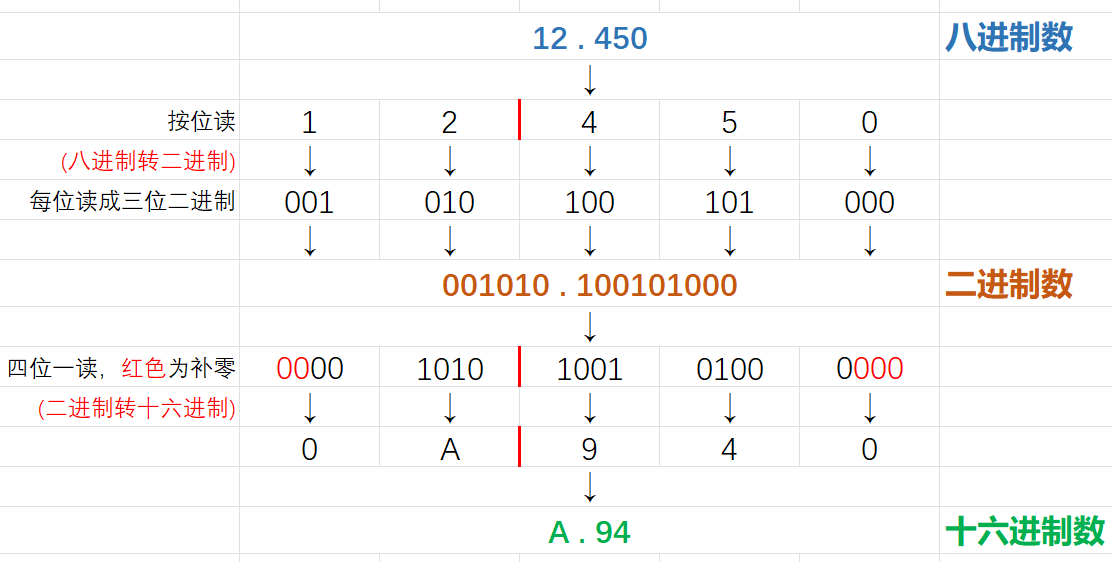
  上圖中我將八進制數12.450先轉換為了二進制數001010.100101000，再轉換為了十六進制數A.94。

  二進制和其他進制互相轉換的方法在上面已經介紹過了，這裡就不多贅述。

• 通過十進制進行間接轉換

  

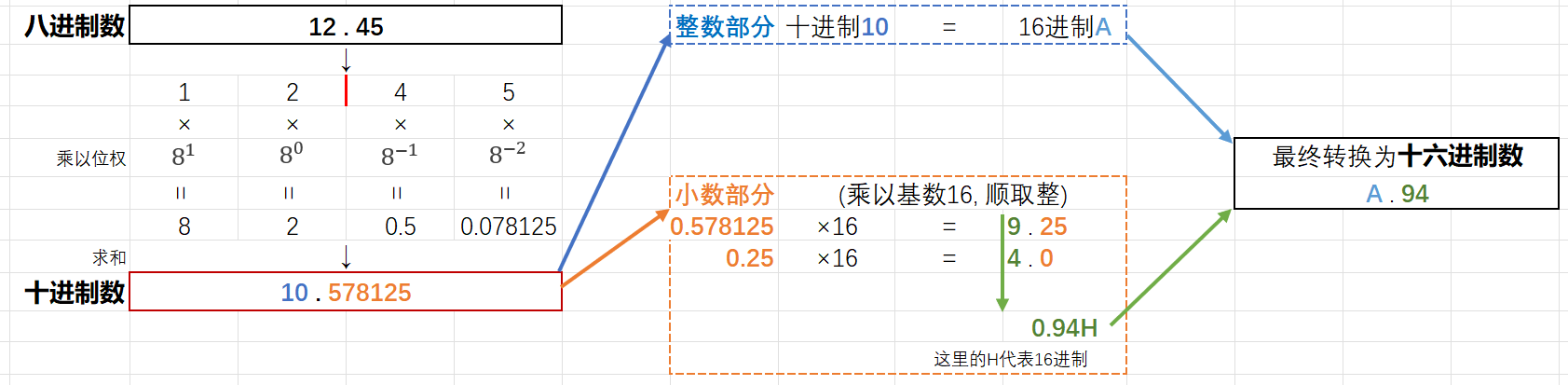
  上圖中我將八進制數12.450先轉換為了十進制數10.578125，再轉換為了十六進制數A.94。

  • 這裡再提一嘴：十進制轉為其他進制時，需將整數和小數分而治之。

  十進制和其他進制互相轉換的方法在上面也已經介紹過了，這裡就不多贅述。

十六進制轉八進制的例子

• 通過二進制進行間接轉換

  

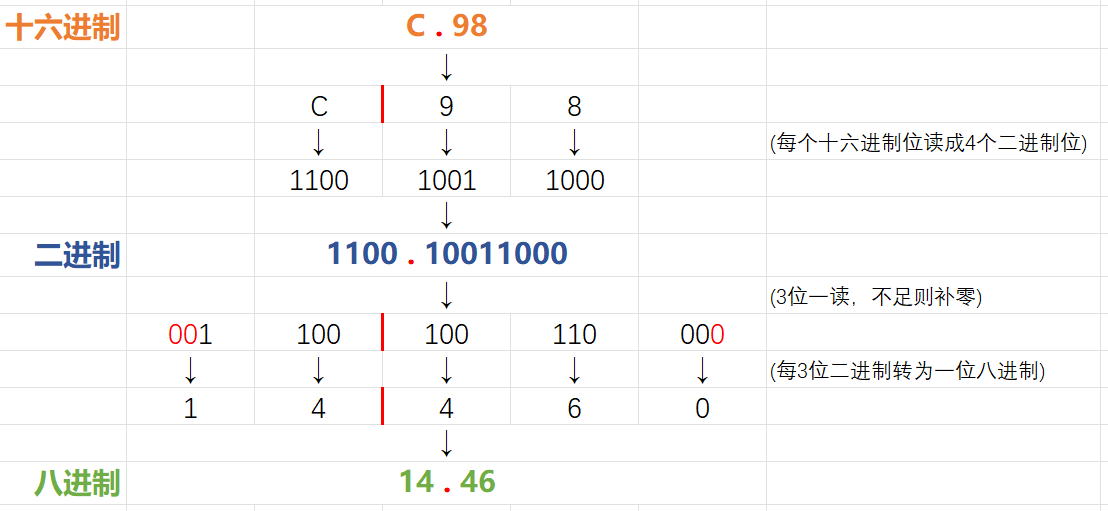
  上圖中我將十六進制數C.98先轉換為了二進制數1100.10011000, 再轉換為了八進制數14.46。

  可以看到，十六進制轉八進制和八進制轉十六進制的過程是十分類似的。

• 通過十進制進行間接轉換

  

  上圖中我將十六進制數C.98先轉換為了十進制數12.59375, 再轉換為了八進制數14.46。

冷笑話

這位老夥計為什麼要在萬聖節前夜穿上聖誕節的服裝呢？

答：因為 Oct 31 = Dec 25。

October(十月) 31 是萬聖節前夜，December(十二月) 25 是聖誕節。
但是在這也可以理解成Octal(八進制) 31 = Decimal(十進制) 25 (*^_^*)