探究Presto SQL引擎(4)-統計計數
作者:vivo互聯網用戶運營開發團隊 – Shuai Guangying
本篇文章介紹了統計計數的基本原理以及Presto的實現思路,精確統計和近似統計的細節及各種優缺點,並給出了統計計數在具體業務使用的建議。
系列文章:
一、背景
學習Hadoop時接觸的第一個樣例就是word count,即統計文本中詞的數量。各種BI、營銷產品中不可或缺的模塊就是統計報表。在常見的搜索分頁模塊,也需要提供總記錄數。
統計在SQL引擎中可謂最基礎、最核心的能力之一。可能由於它太基礎了,就像排序一樣,我們常常會忽視它背後的原理。通常的計數是非常簡單的,例如統計文本行數在linux系統上一個wc命令就搞定了。
除了通常的計數,統計不重複元素個數的需求也非常常見,這種統計稱為基數統計。對於Presto這種分佈式SQL引擎,計數的實現原理值得深入研究,特別是基數統計。關於普通計數和基數計數,最典型的例子莫過於PV/UV。
二、基數統計主要算法
在SQL語法裏面,基數統計對應到count(distinct field)或者aprox_distinct()。通常做精確計數統計需要用到Set這種數據結構。通過Set不僅可以獲得數量信息,還能不重不漏地獲取每一個元素。
Set內部有兩種實現實現原理:Hash和Tree。
在海量數據的前提下,Hash和Tree有一個致命的問題:內存消耗,而且隨着數據量級的增長,內存消耗也是線性增長。
面對Set內存消耗的問題,通常有兩種思路:
-
一種是選取其他內存佔用更小的數據結構,例如bitmap;
-
另一種是放棄精確,從數學上尋求近似解,典型的算法有Linear Count和HyperLogLog。
2.1 Bitmap
在數據庫領域Bitmap並不是新事物,一般用作索引,稱為位圖索引。所謂位圖索引,就是用一個bit位向量來記錄某個字段值是否存在於對應的記錄。它有一個前置條件:記錄要有永久的編號,類似於從1開始的自增主鍵。
2.1.1 位圖向量的構建
舉個例子,假設表user記錄如下:
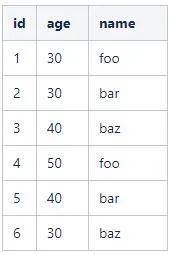
這是很典型的一張數據庫表。對於表中的字段,如何構建位圖索引呢?以age字段為例:
-
S1: 確定字段的取值集合空間: {30,40,50} 一共3個選項。
-
S2: 依次為每個選項構建一個長度為6的bit向量,得到一個3*6的位圖。3表示字段age的取值基數,6表示記錄數。

-
S3: 基於表設置位圖相應向量值。例如:age=30的記錄id分別為{1,2,6},那麼在向量1,2,6位置置為1,其他置為0。得到110001。

同理,對於name字段,其向量位圖為:

可以看出,如果對於數據表的一個字段,如果記錄數為n且字段的取值基數為m,那麼會得到一個m*n的位圖。
2.1.2 位圖向量的應用
有了位圖向量,該如何使用呢?假設查詢SQL為
select count(1) from user where age=40;
則取age字段位圖中age=40的向量:110001。統計其中1的個數,即可得到最終結果。
假設查詢SQL更複雜一些:
select count(1) from user where age=40 and name='baz'
則取age字段位圖中age=40的向量:110001和name=’foo’的向量:100100。兩個向量進行交集運算:

最後統計結果為1。
關於Bitmap的思想,筆者認為最巧妙的一點就是通過位運算實現了集合運算。如下圖所示:

在不同的業務場景中,這裡的集合可以賦予不同的業務含義。
2.1.3 位圖向量的優點
將字段的篩選變成了向量計算後,會非常節約內存,而且可以通過分段長度編碼等方式對bitmap向量進行壓縮。而且位運算直接對內存中的二進制位進行操作,執行效率非常高,是性能提升的一大殺器。
理解了bitmap後,可以發現對於整型字段,可以直接用bitmap進行基數統計。筆者曾經實驗過,對於3億數據量級使用roaringbitmap工具,bitmap消耗內存約30M,而且如果數據分佈非常密集內存消耗還有很大的壓縮空間。唯一的缺點是非數值型字段,需要進行額外的轉換處理。
2.2 Linear Count算法
Linear Count簡稱LC算法,LC算法的流程非常簡單(背後的數學思想不簡單)。
算法描述如下:
-
初始化:給定m個房間,房間存儲數字,初始化為0。
-
迭代執行:對於要進行基數統計的集合,用一個哈希函數處理集合中的每一個元素。通過哈希函數處理後,元素就可以放置到一個房間中。
-
收尾:統計m個房間中空房間的數量U。
-
結論:集合中不重複元素的個數估計值可以通過如下公式計算:n=-m*log(U/m)。
這樣就把一個統計問題轉換成了一個數學問題。公式非常簡潔,看到這裡大腦中一定會出現許多的問題:
這個公式是怎麼得到的?
這裡涉及到概率論與數理統計知識,簡單來說就是分佈、期望、方差、最大似然估計。數學相關的知識比較初級,陳希孺的《概率論與數理統計》基本能覆蓋這個公式的數學原理。
這個算法的精確度怎麼樣?
這個問題從數學的角度,就是問方差(標準差)。這裡沒法給一個具體的值,跟滿桶率控制, m的選擇有關。
這個算法相比精確計數很省空間嗎?
這個毋庸置疑,不然直接精確統計就可以了。
m和最終結果n需要滿足什麼關係?
(畢竟當沒有空房間時,這個公式就有問題了。) 這裡直接給結論吧,隨着m和n的增大,m大約為n的十分之一。
2.3 HyperLogLog算法
HyperLogLog簡稱HLL算法,它有如下的特點:
-
可以實現由極小的內存開銷統計出巨量的數據。在 Redis中實現的HyperLogLog,只需要12K內存就能統計2^64個數據。
-
可以方便實現分佈式擴展。(這個點對算法在業務系統中落地非常關鍵)
理解HLL算法,需要如下幾個知識點的鋪墊:伯努利實驗、調和平均數。
伯努利實驗有很多的呈現方式,本文例舉其中的一種: 取一枚硬幣,不斷拋擲,直到硬幣落地結果為正面朝上。這樣的執行過程稱為一輪實驗。從描述可以看出一輪實驗完成拋擲硬幣的次數是隨機的。
一輪實驗對應的Java代碼實現如下:
private Random random = new Random();
/**
* 0代表正面
* 1代表反面
* 拋擲直到出現正面
* @return 拋擲的次數
*/
public int tossCoin(){
int r,cnt=0;
do{
r=random.nextInt(2);
cnt++;
}while (r<1);
return cnt;
}
可以看出,每執行一輪實驗就會得到一個數字,代表這輪實驗拋擲硬幣的次數。例如:
執行了10輪,可能的結果如下:
3,1,4,1,1,2,3,4,1,1
執行了100輪,可能的結果如下:
1,1,2,1,1,2,1,4,2,1,3,1,1,1,1,3,1,2,1,1,2,4,2,3,2,1,1,1,3,1,2,2,6,1,2,4,1,2,2,1,1,3,1,1,1,1,1,1,1,1,1,4,2,1,1,1,1,1,3,1,2,4,4,4,1,3,2,1,5,1,1,1,1,1,1,1,5,1,1,7,1,1,4,1,3,2,1,1,5,2,1,1,5,2,1,1,4,1,1,1
執行了1000輪,可能的結果如下:
1,2,1,2,1,3,3,3,1,1,2,2,1,2,1,1,1,1,1,2,1,7,1,1,1,2,2,1,1,3,5,2,3,2,3,1,1,3,1, ...,4,1,1,1,2,2,1,3,1,1,1,2,1,1,1,2,1,4,2,2,1,2,2,2,1,1,1,2,2,2,1,1,1,2,2,1,1,3,2,6,1,1,1,2,1,1,1,1,1,1,1,2,1,1,1,1,2,1
這時候問題就來了,我們這樣按上面的規則不停的拋硬幣只是為了應付無聊的時間嗎?當然不是!我們關注的重點是:

當然,這個最大值是隨機變動的,它不是一個固定的值。但是隱約中有個規律:執行的輪次越多,輪次對應的最大值也越大。數學上可以給一個很粗略的公式來擬合這種關係:n=2^p。
換言之,我們可以通過p來估計n。到這裡就出現了問題解決思路的轉換:
將基數統計問題轉換成概率論裏面參數估計的問題。
思維轉換到了數學領域,就可以用數學的工具來解決問題。通常用概率論的思維解決問題,會面臨如下幾個攔路虎。
問題一:最大值不穩定,容易受到極值影響。
在概率上,對於極值我們的處理策略是多實驗幾輪,通過平均值來消除極值的影響。這個就引出了第二基礎知識點:調和平均數。
數學上其實有許多的平均數計算方式:算術平均數、幾何平均數、平方平均數。這裡選用調和平均數主要是消除極值的影響。通常有個笑話說,我的收入是1萬,老闆的收入是1億,我們平均收入是5000萬,我被平均了。如果用調和平均數,得到的結果就是1999.98。
關於調和平均數的公式,非常容易理解:

關於數學,確切地說是概率論的知識點,還有很多。例如估計方法是有偏估計還是無偏估計?,估計的方差和標準差是多大?這裡涉及到較為底層的概率論知識,就先略過。
略過數學知識,關鍵的問題在於,我們如何將待基數統計問題跟上面的伯努利實驗建立聯繫?這兩個點之間的橋樑就是Hash函數。第一次見識到Hash函數還能這樣用,確實大開眼界。

對於相同的數,通過hash函數生成的散列值是相同的,這就進行了排重。當然不排除不同的數據生成同樣的hash值,形成衝突。由於選取的hash函數例如MurmurHash3衝突率低,可以忽略這個因素。
實際上,由於Hash函數生成的二進制串通常具備均勻的特性,所以Hash函數生成的二進制串可以視為拋擲硬幣的結果。
對於一個待進行基數統計的集合(例如一個表中符合條件的字段值),為了降低估計的錯誤率,我們分成m組。某個值歸屬於哪個組由hash函數生成結果對應的前幾位決定,剩下的二進制串用於計算當前輪伯努利實驗第一次出現正面時拋擲的次數,記為p。
所以算法描述如下:

簡單來說就是統計每個組最大的p, 然後用現成的公式計算結果即到達預估的結果。
三、分佈式計數核心流程
對於Hadoop中的入門案例wordcount,可以發現如果用Presto SQL表達如下(以tpch數據集customer表name字段為例):
select w, count(1) cnt from ( select split(name,'#') words from customer ) t1 cross join UNNEST(t1.words) AS t (w) group by w;
可以看出相比大段的代碼,SQL處理對用於來說要簡單的多。無論是哪種表達方式,核心點就是分組統計。
在MapReduce框架核心流程如下:

那麼在Presto, 其執行流程是什麼樣呢?

從邏輯上,都是類似的。先分組聚合,然後匯總聚合。
四、基數統計在Presto中的落地
對於基數統計問題Presto支持兩種實現方式。一種是追求精確的count distinct; 另一種是提供近似統計的approx_distinct。
count distinct的核心細節
以SQL :select count(distinct id) from hive_table 為例。

即以id為主key, 對數據進行hash分發,進行部分聚合,最終整體聚合。依然是map-reduce的思路,只不過數據按id進行了分發。
aprox_distinct的核心細節

這裡就免去了基於id的hash分發策略。所以也減少了一個stage。至於approx_distinct的內部細節,基礎框架airlift中,封裝了HyperLogLog算法的實現,採用的函數是MurMurHash3算法,生成64位散列值。前6位用於計算當前散列值所在分組m。實現過程中還有一個很有意思的細節:基於待統計的數據量,實現中同時採用了Linear Count算法和HyperLogLog算法。
五、業務建議
通過上面的分析,我們可以發現高基數統計是一個非常消耗內存的操作,特別是在分佈式系統背景下,不僅消耗內存,而且涉及大量網絡數據傳輸。如果分析對應的業務場景,可以提供近似值而非精確值,那麼就能大幅度降低系統消耗和響應時間,提升用戶體驗。或者在設計產品的時候,對於一些場景的計數,可以優先提供近似估計,如果用戶確實需要精確計數,那麼在管理好用戶響應時間預期下,再提供查詢精確值的接口。
理解了精確統計和近似統計的細節及各種優缺點,處理問題的思路就會更開闊。例如:在設計存儲索引時,我們可以優先使用HyperLogLog統計一個字段的基數近似值,如果得到的結果不是高基數,那麼我們可以對字段構建bitmap索引,藉此提升數據處理的效率。
在《我們如何走到今天:重塑世界的6項創新 》一書中有這樣一個觀點讓人記憶深刻:我們衡量越精確,控制的能力就越強。但是它沒有說的是,衡量越精確,成本就越大。
參考:
-
《數據庫系統實現》
-
A Linear-Time Probabilistic Counting Algorithm for Database Applications
-
HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm


