面試讓我手寫紅黑樹?!
作者:小傅哥
博客://bugstack.cn
沉澱、分享、成長,讓自己和他人都能有所收穫!😄
一、前言:掛在樹上!
不知道你經歷過HashMap的奪命連環問!
為啥,面試官那麼喜歡讓你聊聊 HashMap?因為 HashMap 涉及的東西廣,用到的數據結構多,問題延展性好,一個 HashMap 就能聊下來80%的數據結構了。而且面試 HashMap 能通過你對紅黑樹的了解定位出你哪個級別的研發人員。
而紅黑樹的知識點可以說是非常龐大,在學習紅黑樹時也不能一下就能掌握,甚至很程序員壓根就沒搞明白紅黑樹,只是背下來它的幾條限定規則而已。
其實一開始我也是這樣! 不過總感覺這塊的知識點不搞個明明白白,就鬧心。因為不可能一個理科的東西,是需要死記硬背搞下來的。所以在翻閱資料、文檔、歷史、典籍,找到紅黑樹的演化過程,它是從2-3樹演變而來,而2-3樹、AVL樹,這類B-樹,也就是 BalancedTree 平衡樹。它們都是為了解決 BST 二叉搜索樹不自平衡而來的產物。
那麼現在清楚了,要想搞定紅黑樹,讓懂了就是真的懂,就需要把前面這些知識搞定,並且除了理論還能用落地的案例代碼編寫出來,才是悟透。好,那麼接下來,小傅哥就帶着你一起搞定這點事
二、BST 樹
Binary Search Tree歷史
二叉搜索樹算法是由包括 PF Windley、Andrew Donald Booth、Andrew Colin、Thomas N. Hibbard 在內的幾位研究人員獨立發現的。該算法歸功於 Conway Berners-Lee 和 David Wheeler ,他們在 1960 年使用它在磁帶中存儲標記數據。 最早和流行的二叉搜索樹算法之一是 Hibbard 算法。
1. 二叉搜索樹數據結構
二叉搜索樹(Binary Search Tree),也稱二叉查找樹。如果你看見有序二叉樹(Ordered Binary tree)、排序二叉樹(Sorted Binary Tree)那麼說的都是一個東西。
- 若任意節點的左子樹不空,則左子樹上所有節點的值均小於它的根節點的值;
- 若任意節點的右子樹不空,則右子樹上所有節點的值均大於它的根節點的值;
- 任意節點的左、右子樹也分別為二叉查找樹;
二叉搜索樹在日常開發中使用的場景還是比較多的,例如基於組合模式實現的規則引擎,它就是一顆二叉搜索樹。但類似這樣的開發中用到的二叉樹場景,都是基於配置生成,所以組合出來的節點也更加方便控制樹高和平衡性。這與 Java API HashMap 中的紅黑樹這樣為了解決插入節點後仍保持樹的平衡性是有所不同的。
所以二叉搜索樹也是一顆沒有經過調衡的基礎性數據結構,在一定概率上它完成有可能退化成鏈表,也就是從近似O(logn)的時間複雜度退化到O(n)。關於二叉搜索樹的平衡解決方案,包括;AVL樹、2-3樹、紅黑樹等,小傅哥會在後續的章節繼續實現。
2. 二叉搜索樹結構實現
二叉搜索樹是整個樹結構中最基本的樹,同時也是樹這個體系中實現起來最容易的數據結構。但之所以要使用基於二叉搜索樹之上的其他樹結構,主要是因為使用數據結構就是對數據的存放和讀取。那麼為了提高吞吐效率,則需要儘可能的平衡元素的排序,體現在樹上則需要進行一些列操作,所以會有不同的結構樹實現。
而實現二叉搜索樹是最好的基礎學習,了解基本的數據結構後才更容易擴展學習其他樹結構。
- 源碼地址://github.com/fuzhengwei/java-algorithms
- 本章源碼://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/tree
2.1 樹枝定義
public Integer value;
public Node parent;
public Node left;
public Node right;
- 用於組成一顆樹的節點,則需要包括;值和與之關聯的三角結構,一個父節點、兩個孩子節點。如果是AVL樹還需要樹高,紅黑樹還需要染色標記。
2.2 插入節點
public Node insert(int e) {
if (null == root) {
root = new Node(e, null, null, null);
size++;
return root;
}
// 索引出待插入元素位置,也就是插入到哪個父元素下
Node parent = root;
Node search = root;
while (search != null && search.value != null) {
parent = search;
if (e < search.value) {
search = search.left;
} else {
search = search.right;
}
}
// 插入元素
Node newNode = new Node(e, parent, null, null);
if (parent.value > newNode.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
size++;
return newNode;
}
- 首先判斷插入元素時候是否有樹根,沒有則會把當前節點創建出一顆樹根來。
- 如果當前樹是有樹根的,則對插入元素與當前樹進行一個節點遍歷操作,找到元素可以插入的索引位置 parent(掛到這個父節點下)。也就是 search 搜索過程。
- 最後就是插入元素,通過給插入值創建一個 Node 節點,並綁定它的父元素,以及把新元素掛到索引到的 parent 節點下。
2.3 索引節點
public Node search(int e) {
Node node = root;
while (node != null && node.value != null && node.value != e) {
if (e < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return node;
}
- 值查找的過程,就是對二叉搜索樹的遍歷,不斷的循環節點,按照節點值的左右匹配,找出最終相當的值節點。
2.4 刪除節點
public Node delete(int e) {
Node delNode = search(e);
if (null == delNode) return null;
return delete(delNode);
}
private Node delete(Node delNode) {
if (delNode == null) return null;
Node result = null;
if (delNode.left == null) {
result = transplant(delNode, delNode.right);
} else if (delNode.right == null) {
result = transplant(delNode, delNode.left);
} else {
// 因為刪除的節點,有2個孩子節點,這個時候找到這條分支下,最左側做小的節點。用它來替換刪除的節點
Node miniNode = getMiniNode(delNode.right);
if (miniNode.parent != delNode) {
// 交換位置,用miniNode右節點,替換miniNode
transplant(miniNode, miniNode.right);
// 把miniNode 提升父節點,設置右子樹並進行掛鏈。替代待刪節點
miniNode.right = delNode.right;
miniNode.right.parent = miniNode;
}
// 交換位置,刪除節點和miniNode 可打印測試觀察;System.out.println(this);
transplant(delNode, miniNode);
// 把miniNode 提升到父節點,設置左子樹並掛鏈
miniNode.left = delNode.left;
miniNode.left.parent = miniNode;
result = miniNode;
}
size--;
return result;
}
private Node getMinimum(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
private Node transplant(Node delNode, Node addNode) {
if (delNode.parent == null) {
this.root = addNode;
}
// 判斷刪除元素是左/右節點
else if (delNode.parent.left == delNode) {
delNode.parent.left = addNode;
} else {
delNode.parent.right = addNode;
}
// 設置父節點
if (null != addNode) {
addNode.parent = delNode.parent;
}
return addNode;
}
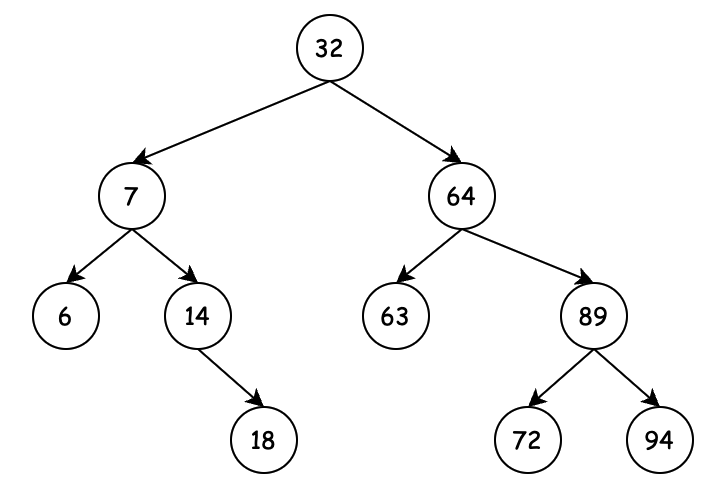
2.4.1 刪除單節點
- 待刪除節點14,判斷此節點的父節點的孩子節點,哪個等於14,找出左右
- 把待刪節點的右孩子節點,掛到刪除節點的右節點
- 給待刪節點的右孩子節點,設置上父節點
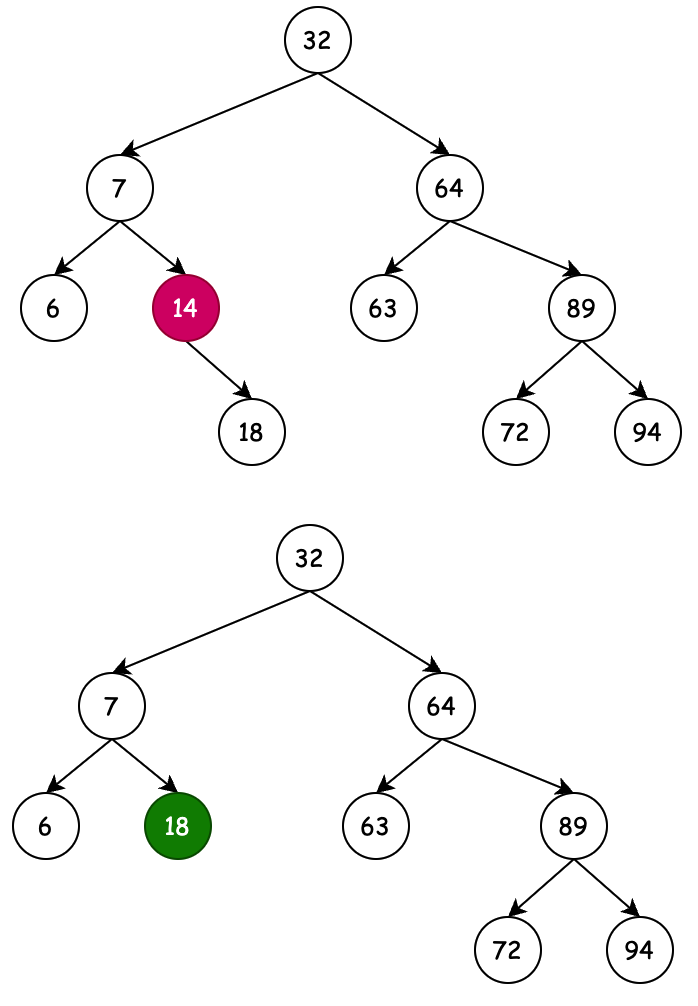
2.4.2 刪除雙節點
- 待刪除節點64,含有雙子節點,則需要根據第一個右子節點查找最小左子節點。從89到72,如果有比72還小的左子節點,繼續排查。
- 排查到節點72,將72這個準備替換待刪元素的節點,與右子節點73進行位置交換,過程與 4.1 相同。使用交換函數 transplant
- 最後是進行節點72與待刪節點64的交換過程,更換三角關係,父節點、左子節點、右子節點。
3. 二叉搜索樹功能測試
為了方便觀察樹結構的變化,這裡小傅哥找了一些資料資料,一種是我們可以通過程序來打印(類似大家之前打印99乘法表,另外是使用線上的可視化圖://visualgo.net/zh/bst?slide=1)
3.1 隨機插入元素
@Test
public void test_binary_search_tree() {
BinarySearchTree tree = new BinarySearchTree();
for (int i = 0; i < 10; i++) {
tree.insert(new Random().nextInt(100));
}
System.out.println(tree);
}
測試結果
/----- 91
| \----- 78
/----- 74
| \----- 67
61
| /----- 51
\----- 40
| /----- 28
\----- 14
\----- 7
Process finished with exit code 0
- 因為你測試時的隨機數不同,可能會出現很多不同結構的二叉搜索樹,也可能是一個類似鏈表結構的退化樹。
3.2 插入並且刪除
@Test
public void test_insert_delete(){
BinarySearchTree tree = new BinarySearchTree();
tree.insert(32);
tree.insert(7);
tree.insert(64);
tree.insert(63);
tree.insert(89);
tree.insert(72);
tree.insert(94);
tree.insert(6);
tree.insert(14);
tree.insert(18);
tree.insert(73);
System.out.println(tree);
// 刪除單節點,只有一個孩子的父節點
// tree.delete(14);
// 刪除雙節點,擁有二個孩子的父節點
tree.delete(64);
System.out.println(tree);
}
測試結果
/----- 94
/----- 89
| | /----- 73
| \----- 72
/----- 64
| \----- 63
32
| /----- 18
| /----- 14
\----- 7
\----- 6
/----- 94
/----- 89
| \----- 73
/----- 72
| \----- 63
32
| /----- 18
| /----- 14
\----- 7
\----- 6
Process finished with exit code 0
- 這個案例就是 刪除雙節點 的案例,刪除了節點64以後,節點72被提取上來使用。讀者夥伴也可以嘗試刪除其他節點測試驗證
三、AVL 樹
AVL樹歷史
在計算機科學中,AVL 樹以其兩位蘇聯發明家Georgy Adelson-Velsky和 Evgenii Landis的名字命名,他們在 1962 年的論文「信息組織算法」中發表了它。它是一種自平衡二叉搜索樹(BST),這是發明的第一個這樣的數據結構。
1. AVL樹數據結構
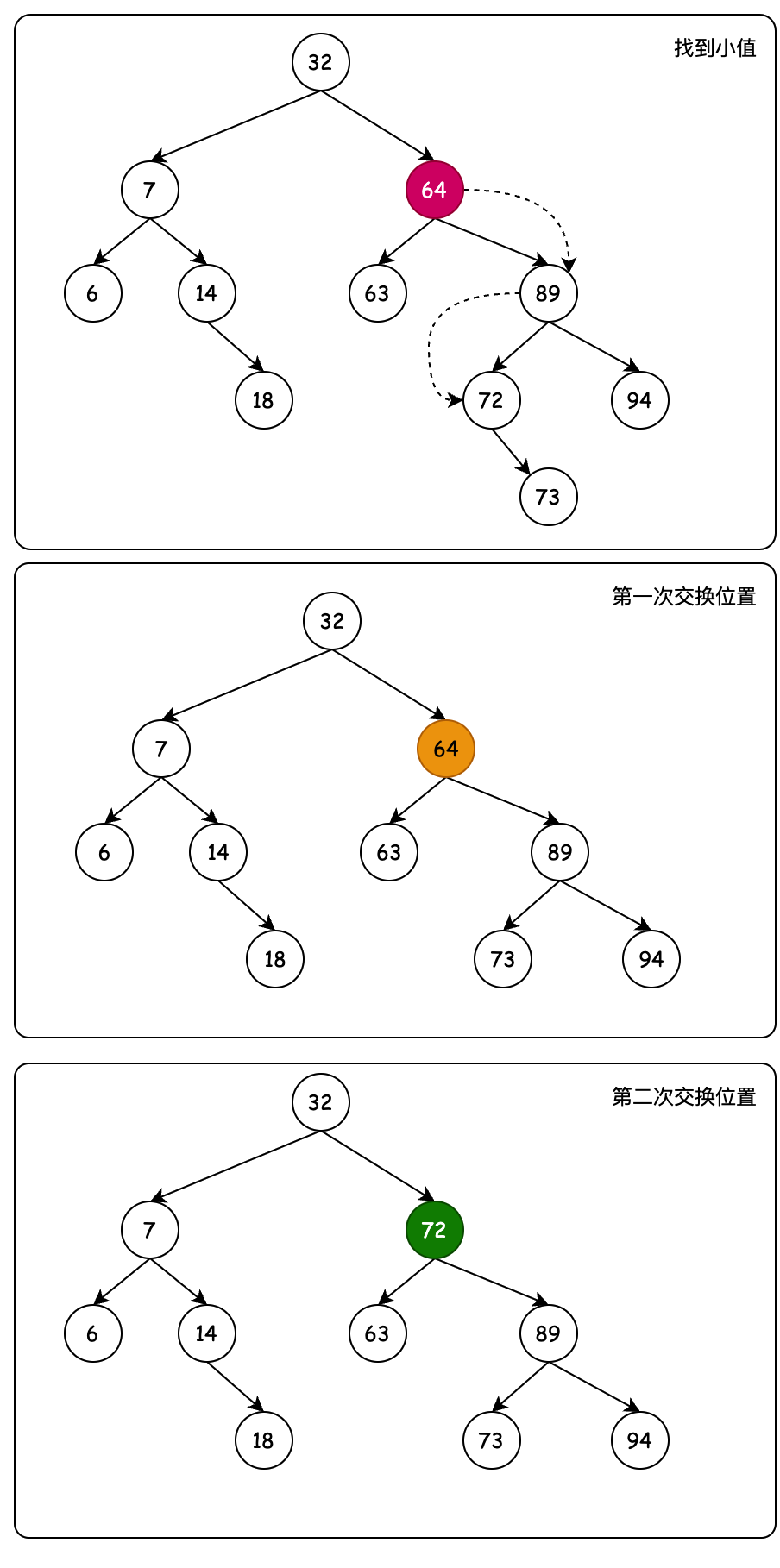
AVL 自平衡二叉樹的出現,其目的在於解決二叉搜索樹退化成鏈表的問題。當我們向BST二叉搜索樹順序存入1、2、3、4、5、6、7個元素時,它會退化成一條鏈表,因而失去樹查詢的時間複雜度,所以我們需要AVL樹平衡樹高。如圖所示
那麼AVL樹是怎麼平衡樹高的呢?
當二叉樹的左右分支樹高差不為1時,需要進行左旋或者右旋,來調衡樹高。這有點像開車的時候,如果車頭偏左就往右打方向盤,車頭偏右就往左打方向盤是一個道理。那這個方向盤(左旋、右旋)是怎麼打的呢,主要分以下四種情況;
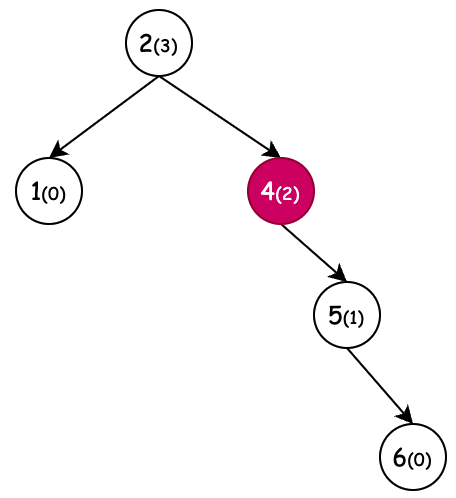
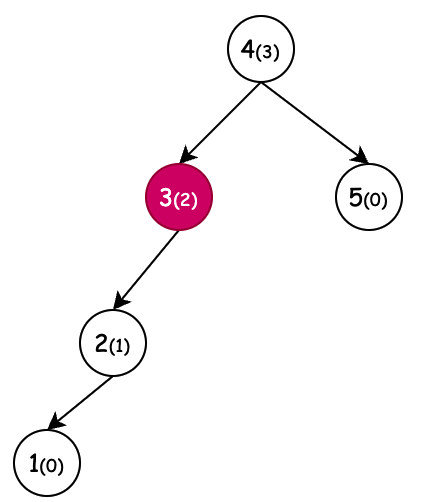
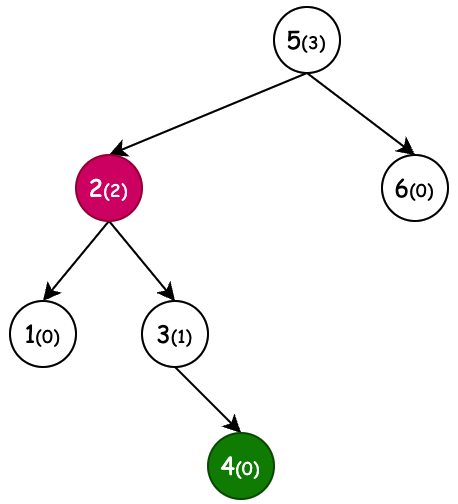
| 左旋(新增節點6) | 右旋(新增節點1) | 左旋+右旋(新增節點4) | 右旋+左旋(新增節點3) |
|---|---|---|---|
 |
 |
 |
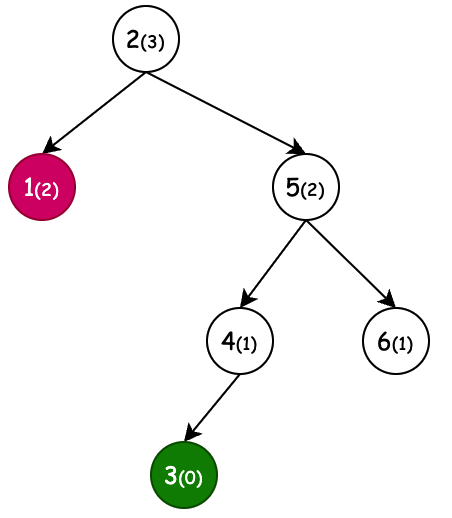 |
| 條件:節點4,平衡因子為-2,左旋 | 條件:節點3,平衡因子為2,右旋 | 條件:節點3,平衡因子為2,右旋。但當節點2平衡因子-1先左旋。 | 條件:節點2,平衡因子為-2,左旋。但當節點5平衡因子1先右旋。 |
-
節點樹高:以節點4為說明,最長的左右分支節點個數,就是節點4的最大樹高。這裡節點4左右孩子節點最長路徑都為2,所以它的樹高為2。同理可計算其他節點樹高。
-
平衡因子:通過當前節點的左右子節點作差計算平衡因子,之後AVL樹通過平衡因子,定義了什麼時候進行左旋和右旋。
-
本章源碼://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/tree
2. AVL樹代碼實現
對於 AVL 樹的實現與 BST 二叉搜索樹相比,在樹的節點定義上多了一個樹高的屬性。也有些AVL樹使用的是平衡因子的屬性,就是通過樹高計算後的結果。樹節點代碼結構如下;
public class Node {
public Class<?> clazz;
public Integer value;
public Node parent;
public Node left;
public Node right;
// AVL 樹所需屬性
public int height;
}
接下來小傅哥就分別通過代碼講解下一顆AVL樹的左旋、右旋、左旋+右旋、右旋+左旋的代碼操作。不要擔心這沒有多複雜,只要你能搞清楚左旋,就能搞清楚右旋。兩旋弄懂組合就沒啥難度了。
- 源碼地址://github.com/fuzhengwei/java-algorithms
- 本章源碼://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/stack
- 動畫演示://visualgo.net/zh/bst?slide=1 —— AVL樹初次理解還是比較困難的,可以結合學習內容的同時做一些動畫演示。
2.1 左旋
圖解左旋操作;它就是一種摘鏈更換調整節點的處理過程,小傅哥把它分解展示,整個過程如下;
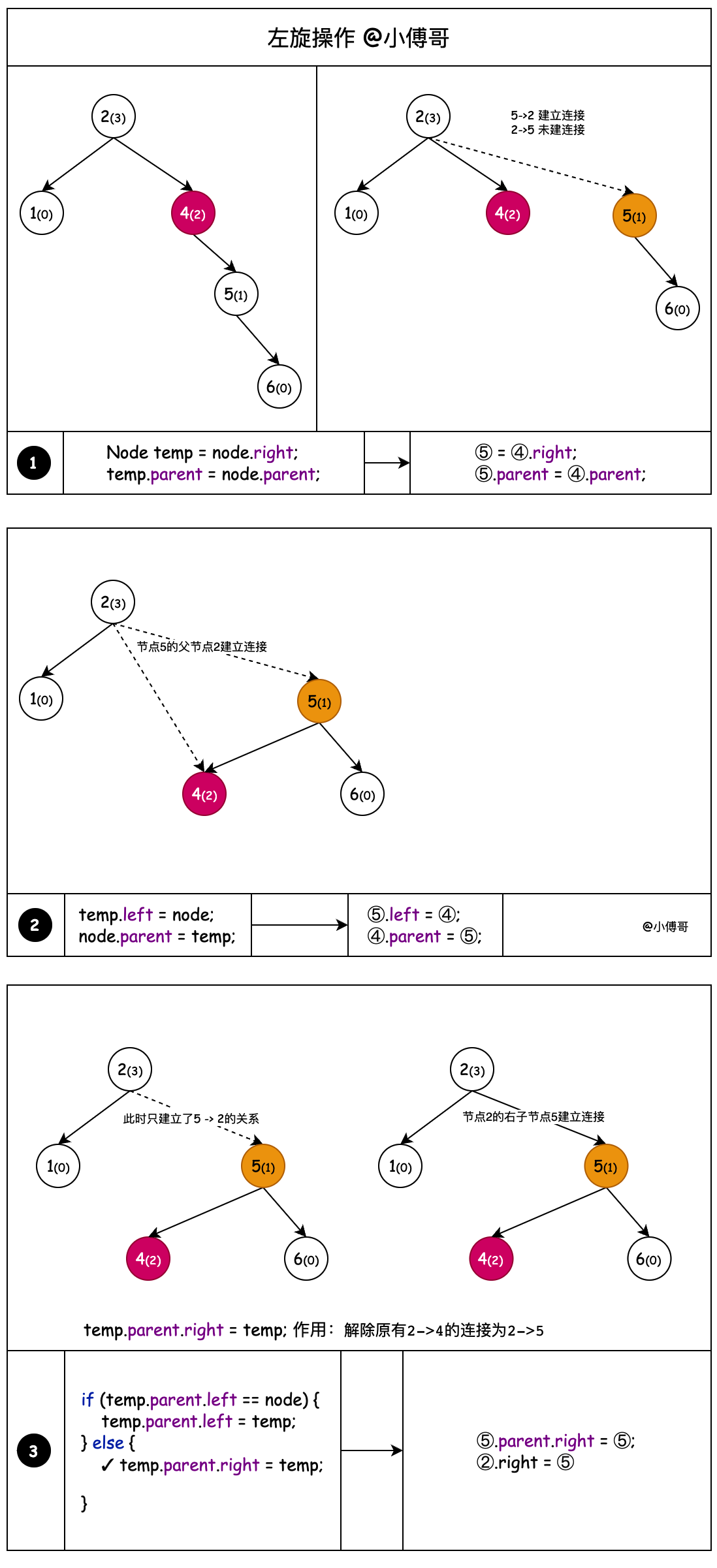
代碼實現
protected Node rotateLeft(Node node) {
Node temp = node.right;
temp.parent = node.parent;
node.right = temp.left;
if (node.right != null) {
node.right.parent = node;
}
temp.left = node;
node.parent = temp;
if (temp.parent == null) {
root = temp;
} else {
if (temp.parent.left == node) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
}
return temp;
}
- 左旋的作用,相當於通過向上遷移樹高差大於1的右子節點來降低樹高的操作。
- 通過節點4拿到父節點2和右子節點5,把父節點2和右子節點5建立關聯
- 節點5的左子節點,相當於是大於4小於4的那麼一個值,只不過這裡不體現。那麼這個節點4的左子節點,應該被遷移到節點3的右子節點上。
- 整理節點5的關係,左子節點為4。左子節點4的父節點為5
- 如果說遷移上來的節點5無父節點,那麼它就是父節點 root = temp
- 遷移上來的節點5,找到原節點4是對應父節點的左子節點還是右子節點,對應的設置節點5的左右位置
2.2 右旋
圖解右旋操作;它就是一種摘鏈更換調整節點的處理過程,小傅哥把它分解展示,整個過程如下;
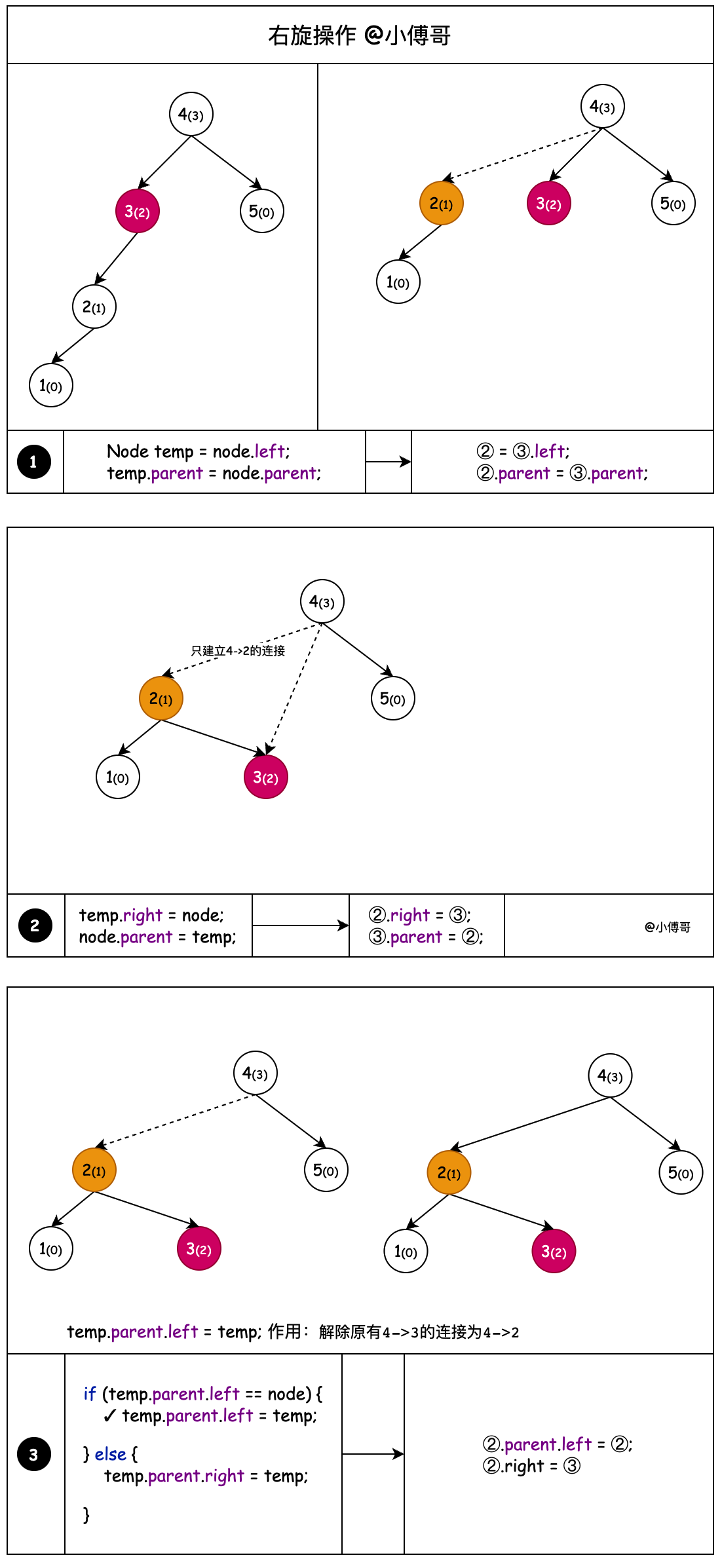
代碼實現
protected Node rotateRight(Node node) {
Node temp = node.left;
temp.parent = node.parent;
node.left = temp.right;
if (node.left != null) {
node.left.parent = node;
}
temp.right = node;
node.parent = temp;
if (temp.parent == null) {
root = temp;
} else {
if (temp.parent.left == node) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
}
return temp;
}
- 右旋的作用,相當於通過向上遷移樹高差大於1的右子節點來降低樹高的操作。
- 通過節點3拿到父節點4和左子節點2,把父節點7和左子節點2建立關聯
- 節點2的右子節點,相當於是大於2小於3的那麼一個值,只不過這裡不體現。那麼這個節點2的右子節點,應該被遷移到節點3的左子節點上。
- 整理節點2的關係,右子節點為3。右子節點3的父節點為2
- 如果說遷移上來的節點2無父節點,那麼它就是父節點 root = temp
- 遷移上來的節點2,找到原節點3是對應父節點的左子節點還是右子節點,對應的設置節點2的左右位置
2.3 左旋 + 右旋
之所以會有左旋 + 右旋,是因為一次右旋操作沒法平衡樹高,而這種樹的不平衡節點的左子節點的右子節點過長,所以要把不平衡節點的左子節點向左旋轉一次,之後再進行右旋操作。
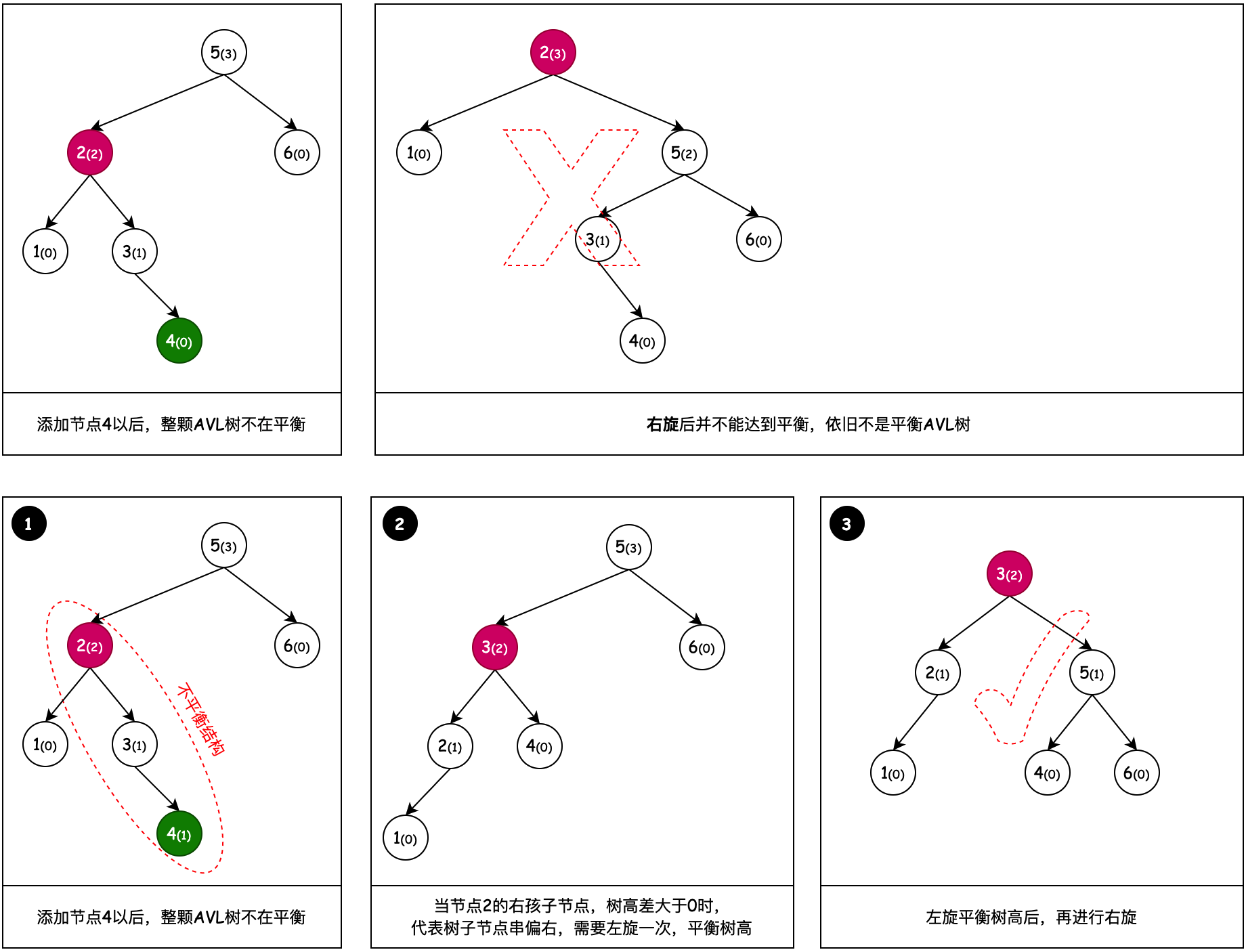
代碼實現
if (factor(node.left) >= 0) {
Node temp = super.rotateRight(node);
refreshHeight(temp.right);
refreshHeight(temp);
} else {
Node temp = super.rotateLeft(node.left);
refreshHeight(temp.left);
refreshHeight(temp);
node.left = temp;
temp = super.rotateRight(node);
refreshHeight(temp.right);
refreshHeight(temp);
}
2.4 右旋 + 左旋
之所以會有右旋 + 左旋,是因為一次左旋操作沒法平衡樹高,而這種樹的不平衡節點的右子節點的左子節點過長,所以要把不平衡節點的右子節點向右旋轉一次,之後再進行左旋操作。
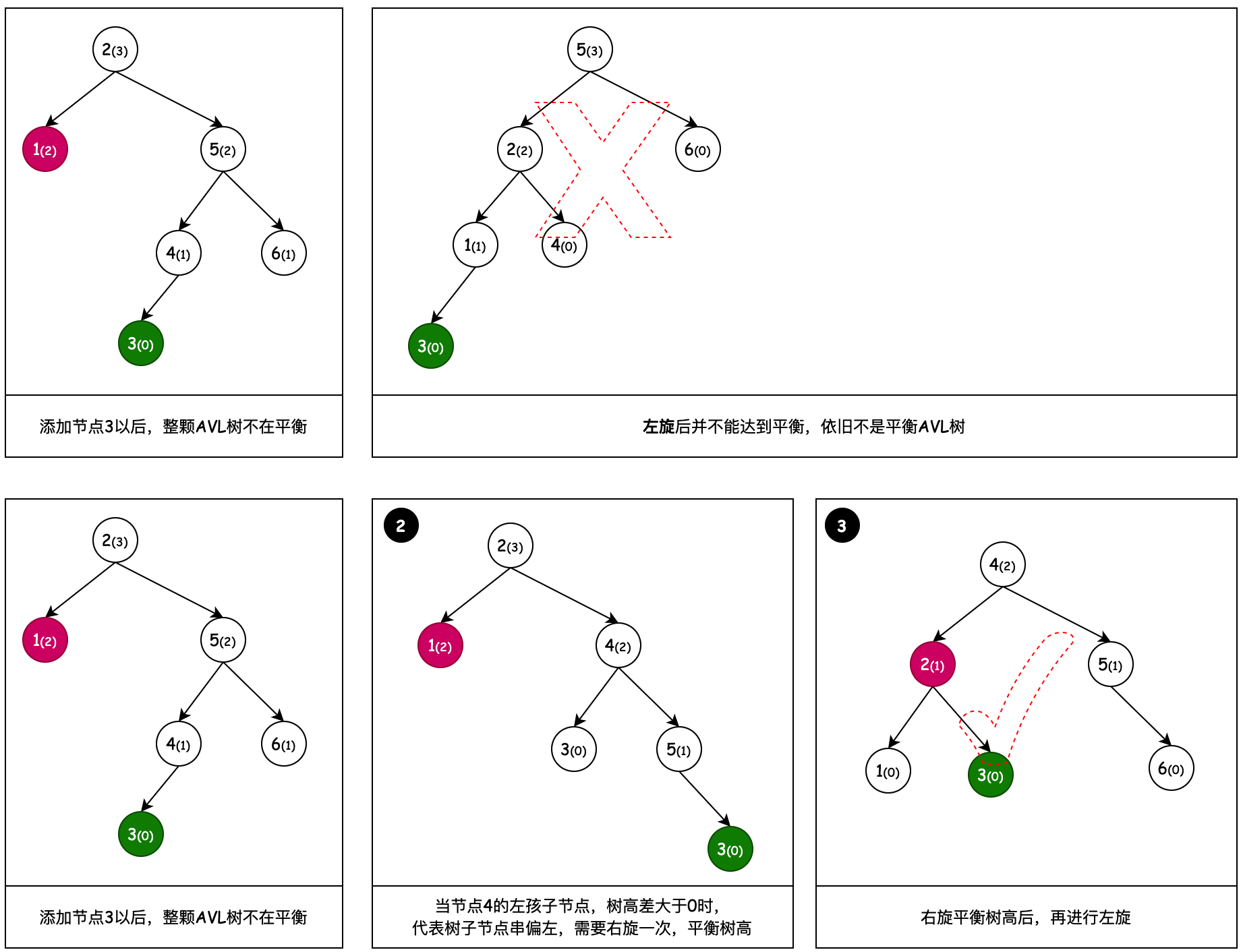
代碼實現
if (factor(node.right) <= 0) {
Node temp = super.rotateLeft(node);
refreshHeight(temp.left);
refreshHeight(temp);
} else {
Node temp = super.rotateRight(node.right);
refreshHeight(temp.right);
refreshHeight(temp);
node.right = temp;
temp = super.rotateLeft(node);
refreshHeight(temp.left);
refreshHeight(temp);
}
3. AVL樹功能測試
為了驗證AVL樹的實現正確與否,這裡我們做一下隨機節點的插入,如果它能一直保持平衡,那麼它就是一顆可靠 AVL 平衡樹。
單元測試
@Test
public void test_random() {
AVLTree tree = new AVLTree();
for (int i = 0; i < 30; i++) {
tree.insert(new Random().nextInt(100));
}
System.out.println(tree);
}
測試結果
輸入節點:61,3,34,82,1,75,56,65,87,18,3,96,53,50,42,24,69,11,95,69,1,1,84,22,5,70,28,55,38,92
/----- 96(0)
/----- 95(1)
| \----- 92(0)
/----- 87(2)
| | /----- 84(0)
| \----- 82(1)
/----- 75(3)
| | /----- 70(0)
| | /----- 69(1)
| \----- 69(2)
| \----- 65(0)
61(5)
| /----- 56(1)
| | \----- 55(0)
| /----- 53(2)
| | | /----- 50(0)
| | \----- 42(1)
| | \----- 38(0)
\----- 34(4)
| /----- 28(0)
| /----- 24(1)
| | \----- 22(0)
| /----- 18(2)
| | \----- 11(1)
| | \----- 5(0)
\----- 3(3)
| /----- 3(1)
| | \----- 1(0)
\----- 1(2)
\----- 1(0)
Process finished with exit code 0
- 隨機插入30個節點,每個節點的順序已經打印,經過AVL左右旋調衡後,二叉結構始終保持樹高平衡因子不超過1,那麼驗證通過。
四、2-3樹
這時候大部分資料會用2-3樹來講解紅黑樹,不過又不去實現一個2-3樹,只是用了一個理論套另外一個理論。雖然能從理解上多一些參考,但始終感覺沒有抓手呀。對於理科思維來說,你得給我東西呀。老是整這懸得楞的🥶誰能受了。所以這裡我們先來用Java實現一個2-3樹,有了基礎再學習紅黑樹
1. 2-3樹數據結構
2–3樹是一種樹型數據結構,由約翰·霍普克洛夫特於1970年發明。它通過在一個節點存放1-2個元素來平衡樹高。從而也使2-3樹存在2叉節點和3叉節點。
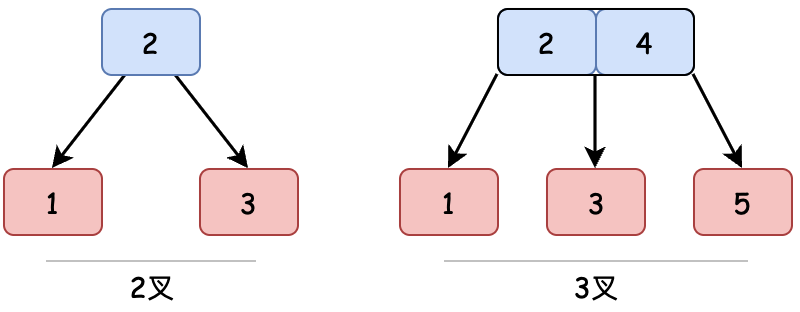
這裡要提到一點,在BST二叉搜索樹可能退化成鏈表的基礎上。引出了自平衡二叉樹,也就是包括上一章實現的AVL樹和Java API HashMap中用到的紅黑樹,它們都屬於BalancedTree,也統稱為B樹,平衡的意思。
而本章實現的2-3樹也是一種簡單的平衡樹,其中每個具有子節點(內部節點)的節點要麼有兩個子節點(2 節點)和一個數據元素,要麼有三個子節點(3 節點)和兩個數據元素。另外 2-3 樹是3階B 樹,2-3-4 樹是4階B樹。
在實現2-3樹之前,先通過圖稿演示下在2-3樹中順序插入1、2、3、4、5、6、7,七個元素時,2-3樹的調衡處理。
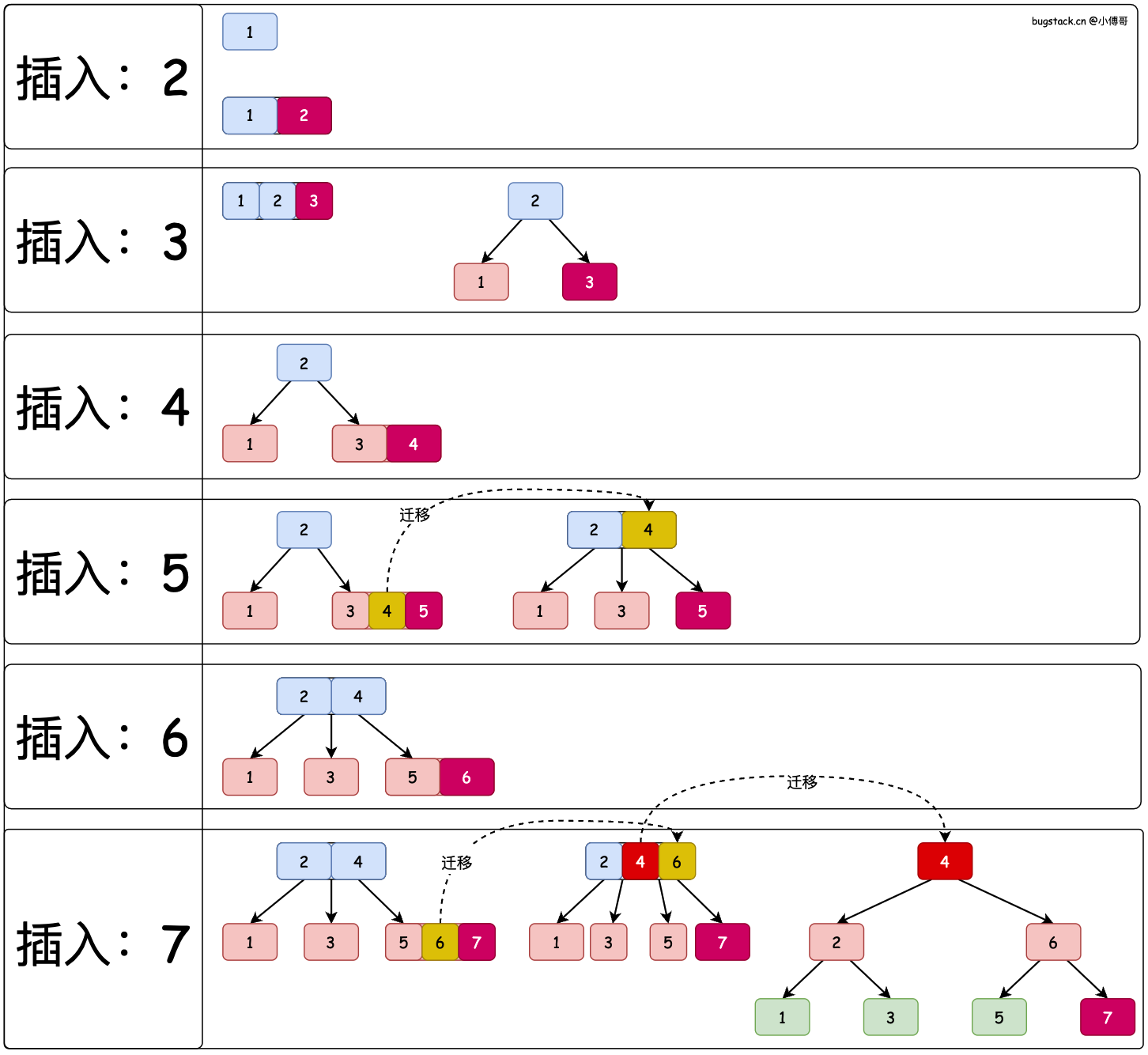
- 2-3 樹的插入過程與 BST 樹類似,會通過樹的左右節點大小,找到自己的插入位置。
- 一個節點可以右1-3個元素,但當元素個數為3時,則需要調衡。把三個節點的中間節點晉陞上來,其餘兩個節點為子節點。
- 如果進行一次調衡後,上一層父節點達到3個元素,則需要2次調衡,來滿足2-3樹的規則。
咋樣,是不看過這個圖之後對於2-3樹的實現已經有感覺了,想動手寫寫試試了?
- 源碼地址://github.com/fuzhengwei/java-algorithms
- 本章源碼://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/tree
2. 2-3樹結構實現
2-3 樹的實現並不複雜,但在實現前要思考🤔以下幾個問題;
- Node 節點屬性信息都包括什麼?
- 插入值,是否需要創建新的 Node?
- 插入後,節點內有3個元素後,怎麼遷移元素?
2.1 節點定義
public class Node_2_3 {
// 元素
public int[] items;
// 序號
public int number;
// 孩子
public Node_2_3[] children;
// 父親【非必須】
public Node_2_3 parent;
public Node_2_3() {
this.items = new int[3];
this.number = 0;
this.children = new Node_2_3[4];
this.parent = null;
}
public void insert(int e) {
int idx = this.number - 1;
while (idx >= 0) {
if (this.items[idx] < e) break;
this.items[idx + 1] = this.items[idx];
--idx;
}
this.items[idx + 1] = e;
++this.number;
}
// ... 省略部分代碼
}
- 2-3樹的幾點元素需要包括;一個數組的元素集合、元素的序號、孩子元素。因為一個節點最多可臨時放入3個元素,那麼就會最多有4個孩子元素,所以孩子元素也是一個數組並且在構造函數中按照4個元素進行初始化。
- 由於本身2-3樹插入元素的開始階段,並不是直接創建一個新的節點,而是在初始化的數組空間中存入元素。所以在節點中提供了一個插入元素的方法 insert 來處理新增元素。
- 另外2-3樹的節點類,還提供了一個方便查詢的方法。包括:獲取左邊元素、中間元素、右邊元素,以及最小值、最大值和判斷是否有孩子節點。這些內容可以源碼。
2.2 拆分節點
當一個節點內有3個元素的時候,就要發起拆分東西,拆分的過程分為;
- 對3個節點的中間節點,插入到父節點上。
- 剩餘2個節點創建出新的節點。
- 建立父節點和新創建的2個節點間關係。
整個操作流程如圖所示
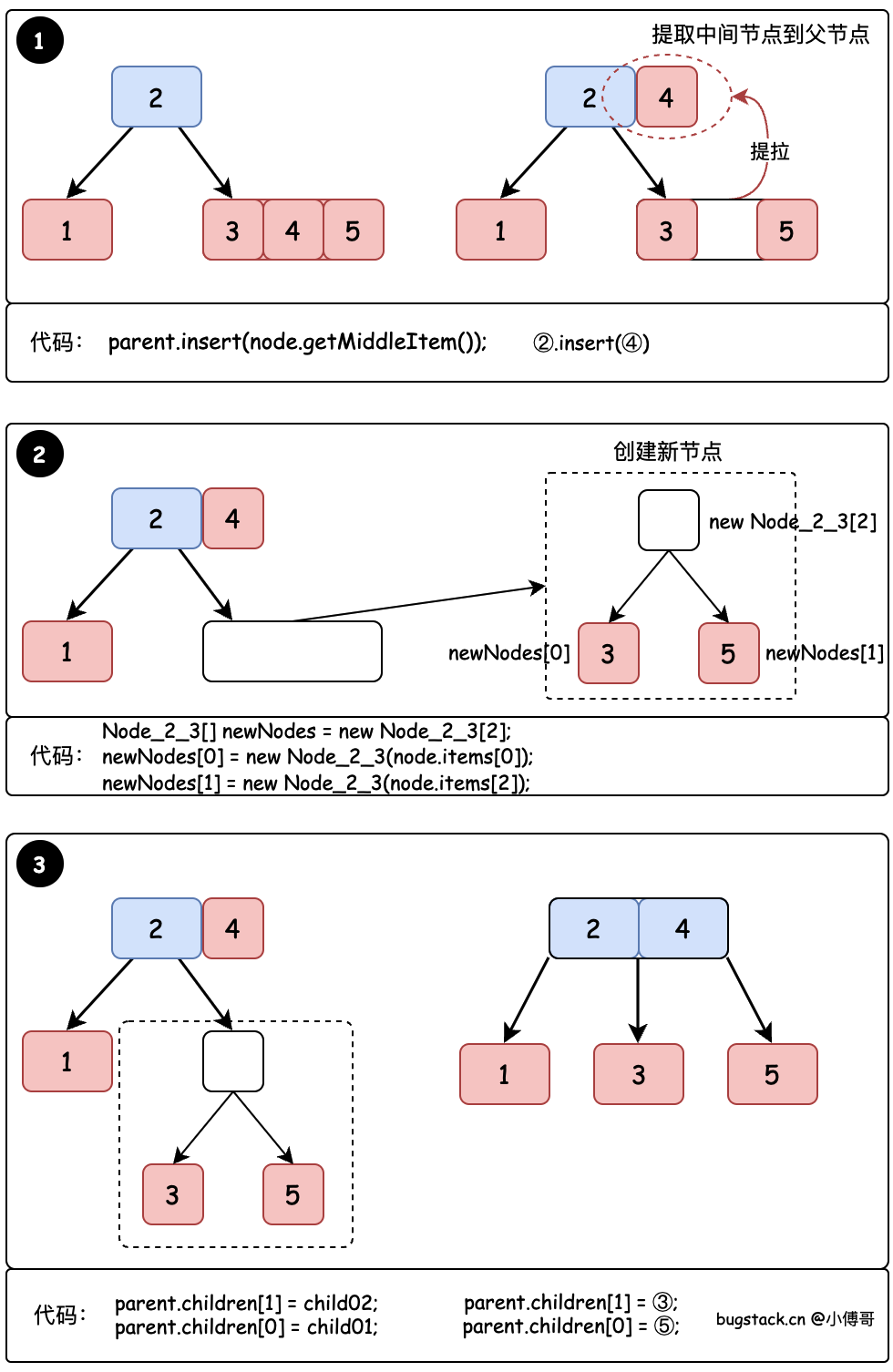
2.1 插入父節點
private Node_2_3 split(Node_2_3 node, Node_2_3 parent) {
if (parent == null) {
parent = new Node_2_3(node);
}
parent.insert(node.getMiddleItem());
Node_2_3[] newNodes = this.triangle(node);
this.replaceChild(parent, node, newNodes[0], newNodes[1]);
return parent;
}
- 整個2-3樹拆分的過程就是在 split 這個方法里,第一步解決了是否有父節點,沒有則創建。
- 之後將原節點的中間值插入到父節點中。接下來的操作就是拆分新節點和更換孩子節點建立新連接。
2.2 拆分新節點
private Node_2_3[] triangle(Node_2_3 node) {
Node_2_3[] newNodes = new Node_2_3[2];
newNodes[0] = new Node_2_3(node.items[0]);
newNodes[1] = new Node_2_3(node.items[2]);
if (!node.isLeaf()) {
// 左孩子
newNodes[0].children[0] = node.children[0];
newNodes[0].children[1] = node.children[1];
// 右孩子
newNodes[1].children[0] = node.children[2];
newNodes[1].children[1] = node.children[3];
}
return newNodes;
}
- 基於傳遞進來的節點,將節點的左右孩子創建新節點,如果這個孩子節點還有分支節點,則一併更新。
2.3 建立新連接
private void replaceChild(Node_2_3 parent, Node_2_3 oldChild, Node_2_3 child01, Node_2_3 child02) {
if (oldChild == parent.children[0]) {
parent.children[3] = parent.children[2];
parent.children[2] = parent.children[1];
parent.children[1] = child02;
parent.children[0] = child01;
} else if (oldChild == parent.children[1]) {
parent.children[3] = parent.children[2];
parent.children[2] = child02;
parent.children[1] = child01;
} else {
parent.children[3] = child02;
parent.children[2] = child01;
}
}
- 建立新連接需要判斷這個節點 oldChild 是父節點的左、中、右,之後進行依次的更換。
- 如拆分節點的介紹圖中,用到的就是
parent.children[1] = child02;parent.children[0] = child01;兩步操作過程。
2.3 新增節點
public void insert(int e) {
// 記錄元素
elementList.add(e);
// 插入元素
if (root == null) {
root = new Node_2_3(e);
} else {
root = insert(e, root);
if (root.number == 3) {
root = split(root, null);
}
}
}
private Node_2_3 insert(int e, Node_2_3 parent) {
if (parent.isLeaf()) {
parent.insert(e);
return parent;
}
Node_2_3 child = null;
if (parent.number == 1) {
if (e < parent.getMinItem()) {
child = insert(e, parent.getLeft());
} else {
child = insert(e, parent.getMiddle());
}
} else {
if (e < parent.getMinItem()) {
child = insert(e, parent.getLeft());
} else if (e > parent.getMiddleItem()) {
child = insert(e, parent.getRight());
} else {
child = insert(e, parent.getMiddle());
}
}
if (child.number == 3) {
return this.split(child, parent);
}
return parent;
}
- 新增節點的過程就比較簡單了,一種是使用遞歸找到可以插入的位置,另外一種就是 where 循環。我們再BST、AVL兩種數據結構種都是用了 where 循環。
- 在2-3樹中 insert 方法遞歸到對應的插入位置後,開始插入元素。當插入元素結束後判斷這個節點是否已經達到了3個節點,如果是則進行拆分。拆分就調用了上面的步驟
3. 2-3樹結構測試
為了讓讀者更好的理解2-3樹的結構,小傅哥在程序的控制台打印了插入的過程。網上沒有2-3樹在線的動畫演示,如果讀者看到也可以留言給小傅哥
@Test
public void test_insert_incr() {
Tree_2_3 tree = new Tree_2_3();
for (int i = 1; i <= 10; i++) {
tree.insert(i);
System.out.println(tree);
}
}
- 順序插入10個節點,如果這是一顆BST樹,它將會退化成鏈表。那麼我們使用自平衡的2-3樹,來看看它的插入效果。
測試效果
輸入節點(1個):1
[1]
輸入節點(2個):1,2
[1,2]
輸入節點(3個):1,2,3
/----- [3]
[2]
\----- [1]
輸入節點(4個):1,2,3,4
/----- [3,4]
[2]
\----- [1]
輸入節點(5個):1,2,3,4,5
/----- [5]
[2,4]---- [3]
\----- [1]
輸入節點(6個):1,2,3,4,5,6
/----- [5,6]
[2,4]---- [3]
\----- [1]
輸入節點(7個):1,2,3,4,5,6,7
/----- [7]
/----- [6]
| \----- [5]
[4]
| /----- [3]
\----- [2]
\----- [1]
輸入節點(8個):1,2,3,4,5,6,7,8
/----- [7,8]
/----- [6]
| \----- [5]
[4]
| /----- [3]
\----- [2]
\----- [1]
輸入節點(9個):1,2,3,4,5,6,7,8,9
/----- [9]
/----- [6,8]---- [7]
| \----- [5]
[4]
| /----- [3]
\----- [2]
\----- [1]
輸入節點(10個):1,2,3,4,5,6,7,8,9,10
/----- [9,10]
/----- [6,8]---- [7]
| \----- [5]
[4]
| /----- [3]
\----- [2]
\----- [1]
Process finished with exit code 0
- 有了這樣的數據結構示意,是不是再來看2-3樹就非常清晰了。—— 我說過,理科生 + 技術,不要只拋理論,要看效果的!東西到手了,能拿捏了,再補充理論。
五、紅黑樹
紅黑樹的歷史
紅黑樹(Red Black Tree)是一種自平衡二叉查找樹,於 1972 年由 Rudolf Bayer 發明的對稱二叉B樹演化而來,並以2-3-4樹、2-3樹流行。最終在 1978 年由 Leonidas J. Guibas 和 Robert Sedgewick 從對稱二叉 B 樹中推導出紅黑樹。PS:之所以選擇「紅色」,是因為它是作者在Xerox PARC工作時可用的彩色激光打印機產生的最好看的顏色。
1. 紅黑樹數據結構
建立在 BST 二叉搜索樹的基礎上,AVL、2-3樹、紅黑樹都是自平衡二叉樹(統稱B-樹)。但相比於AVL樹,高度平衡所帶來的時間複雜度,紅黑樹對平衡的控制要寬鬆一些,紅黑樹只需要保證黑色節點平衡即可。也正因紅黑樹在插入和刪除時不需要太多的平衡操作,也讓它成為;Java中HashMap的元素碰撞後的轉換、Linux的CFS進行調度算法、多路復用技術的Epoll等各類底層的數據結構實現。
但紅黑樹並不是一個那麼容易理解的知識點,甚至很多資料都只是給出紅黑樹的理論,但為什麼要染色、為什麼要左旋、為什麼還要左旋接右旋。這樣的知識點本就不應該是考死記硬背來學習的,這根本不是學習編程的」套路「。—— 你背的再溜,也沒法理解核心本質,忘也只是時間的問題!
其實根據紅黑樹的歷史來看,最早紅黑樹就是來自於2-3樹的結構,所以要學習清楚的結構就要學習 2-3樹。但同時對於 2-3樹的學習也不能只是依靠一份理論,否則對於紅黑的學習來看,就是用不太理解的 2-3樹理論套紅黑樹理論,依舊沒法理解。所以小傅哥在上一章專門講解了 2-3樹,並做了具體的代碼實現。
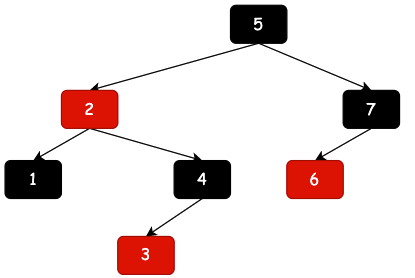
現在來本章,我們在來看看紅黑樹與2-3樹的關係;
| 紅黑樹 | 紅黑樹 | 2-3樹 |
|---|---|---|
 |
 |
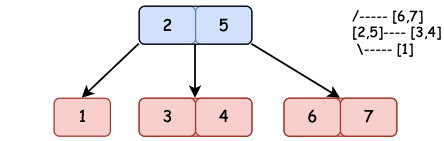 |
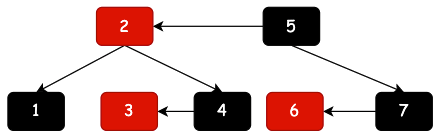
| 一棵標準二叉紅黑樹 | 紅黑樹演化(紅色節點拉平) | 最終恢復到2-3樹 |
紅黑樹一棵在2-3樹基礎上的左傾紅黑樹,這樣就可以把紅色節點與對應的父節點拉平,再把兩個拉平的節點放到一個節點中。就是我們熟悉的2-3樹了。如果你還沒有學習過2-3樹,最好先看下小傅哥的2-3樹,否則你會看的很吃力
現在再來看下紅黑樹的五條定義;
- 每個節點不是紅色就是黑色。
- 黑色決定平衡,紅色不決定平衡。這對應了2-3樹中一個節點內可以存放1~2個節點。
- 根是黑色的。
- 這條規則有時會被省略。由於根總是可以從紅色變為黑色,但不一定相反,因此該規則對分析幾乎沒有影響。
- 所有葉子 (NIL) 都是黑色的。
- 這裡指的是紅黑樹都會有一個空的葉子節點,是紅黑樹自己的規則。
- 如果一個節點是紅色的,那麼它的兩個子節點都是黑色的。
- 通常這條規則也叫不會有連續的紅色節點。這體現在2-3樹中,一個節點最多臨時會有3個節點,中間是黑色節點,左右是紅色節點。2-3樹中出現這樣的情況後,會進行節點遷移,中間節點成為父節點,左右節點成為子節點。
- 從給定節點到其任何後代 NIL 節點的每條路徑都包含相同數量的黑色節點。
- 對應2-3樹中,每一層都只是有一個節點貢獻了樹高決定平衡性,也就是對應紅黑樹中的黑色節點。
好啦,現在再看這5條理論是不就不需要再死記硬背了。因為編程本就是對數學邏輯的具體實現,只要把核心邏輯理順其實很好理解。接下來小傅哥就帶着大家動手實現一下紅黑樹。
2. 紅黑樹結構實現
基於 BST 二叉搜索樹的基礎上,AVL樹添加了樹高作為計算平衡因子的條件,那麼紅黑樹也需要添加一個新的顏色屬性,用於處理平衡操作。
public class Node {
public Class<?> clazz;
public Integer value;
public Node parent;
public Node left;
public Node right;
// AVL 樹所需屬性
public int height;
// 紅黑樹所需屬性
public Color color = Color.RED;
}
相比於AVL樹通過左右旋轉平衡樹高,紅黑樹則是在2-3樹的基礎上,只對黑色節點維護樹高,所以它會使用到染色和左右旋來對樹高調衡。染色與左右旋相比,減少了平衡操作
- 源碼地址://github.com/fuzhengwei/java-algorithms
- 本章源碼://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/tree
- 動畫演示://www.cs.usfca.edu/~galles/visualization/RedBlack.html—— 紅黑樹初次理解還是比較困難的,可以結合學習內容的同時做一些動畫演示。
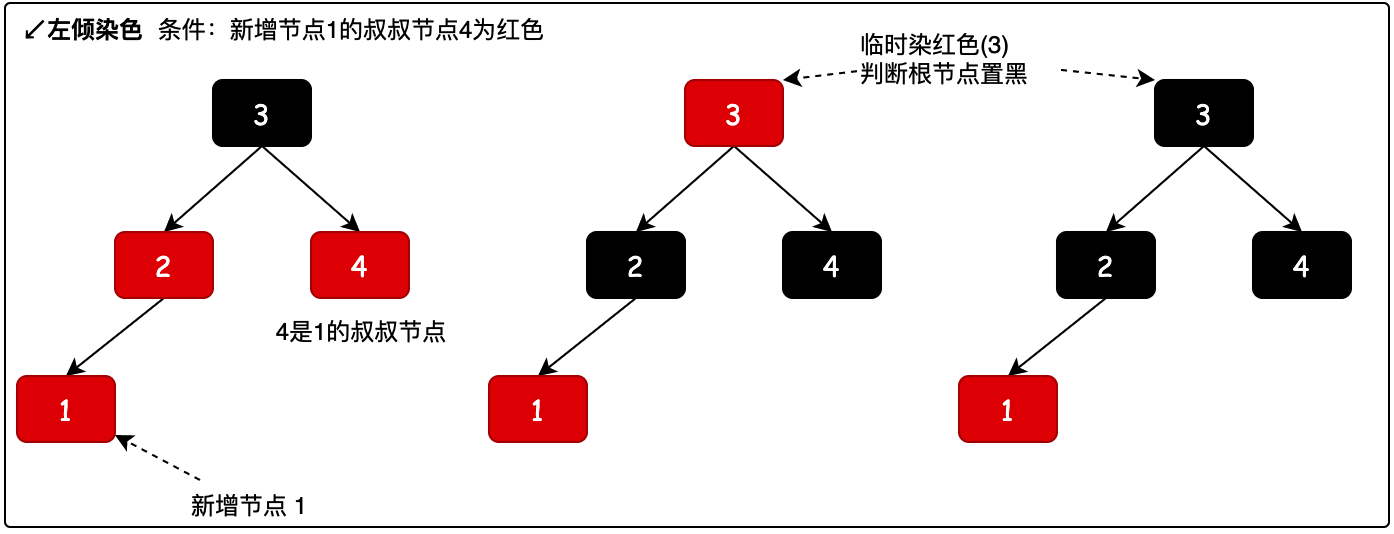
2.1 左傾染色
新增節點1,相當於2-3樹中在節點2上添加了一個節點,這個時候並不影響樹高,只需要染色保持紅黑樹的規則即可。染色過程如圖所示。
Node uncle = grandParent.right;
// 染色
if (uncle.color == Node.Color.RED){
parent.color = Node.Color.BLACK;
uncle.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
current = grandParent;
}
- 染色時根據當前節點的爺爺節點,找到當前節點的叔叔節點。
- 再把父節點染黑、叔叔節點染黑,爺爺節點染紅。但爺爺節點染紅是臨時的,當平衡樹高操作後會把根節點染黑。具體參考源碼
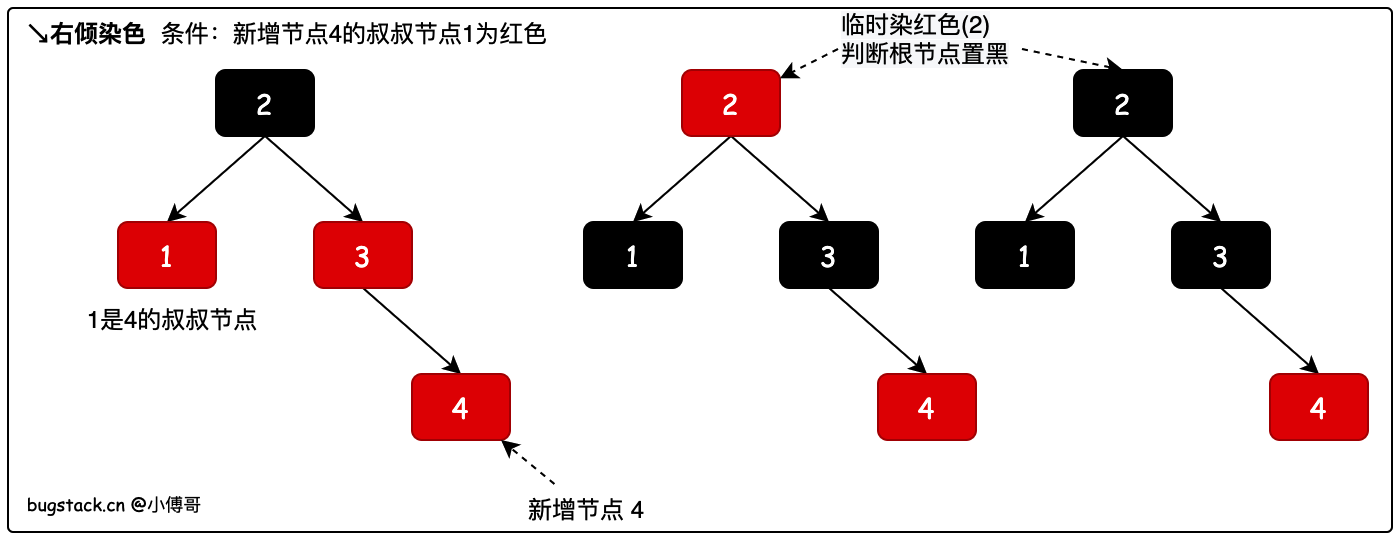
2.2 右傾染色
新增節點4,相當於2-3樹中在節點3上添加了一個節點,這個時候並不影響樹高,只需要染色保持紅黑樹的規則即可。染色過程如圖所示。
Node uncle = grandParent.left;
// 染色
if(uncle.color == Node.Color.RED){
parent.color = Node.Color.BLACK;
uncle.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
current= grandParent;
}
- 染色時根據當前節點的爺爺節點,找到當前節點的叔叔節點。
- 再把父節點染黑、叔叔節點染黑,爺爺節點染紅。但爺爺節點染紅是臨時的,當平衡樹高操作後會把根節點染黑。具體參考源碼
2.3 左旋調衡
2.3.1 一次左旋
對照2-3樹,只有當一個節點內有3個節點的時候,才需要調衡。那麼紅黑樹則是判斷當前節點的叔叔節點是否為紅色節點,如果不是則沒法通過染色調衡,也就是需要選擇進行調衡。
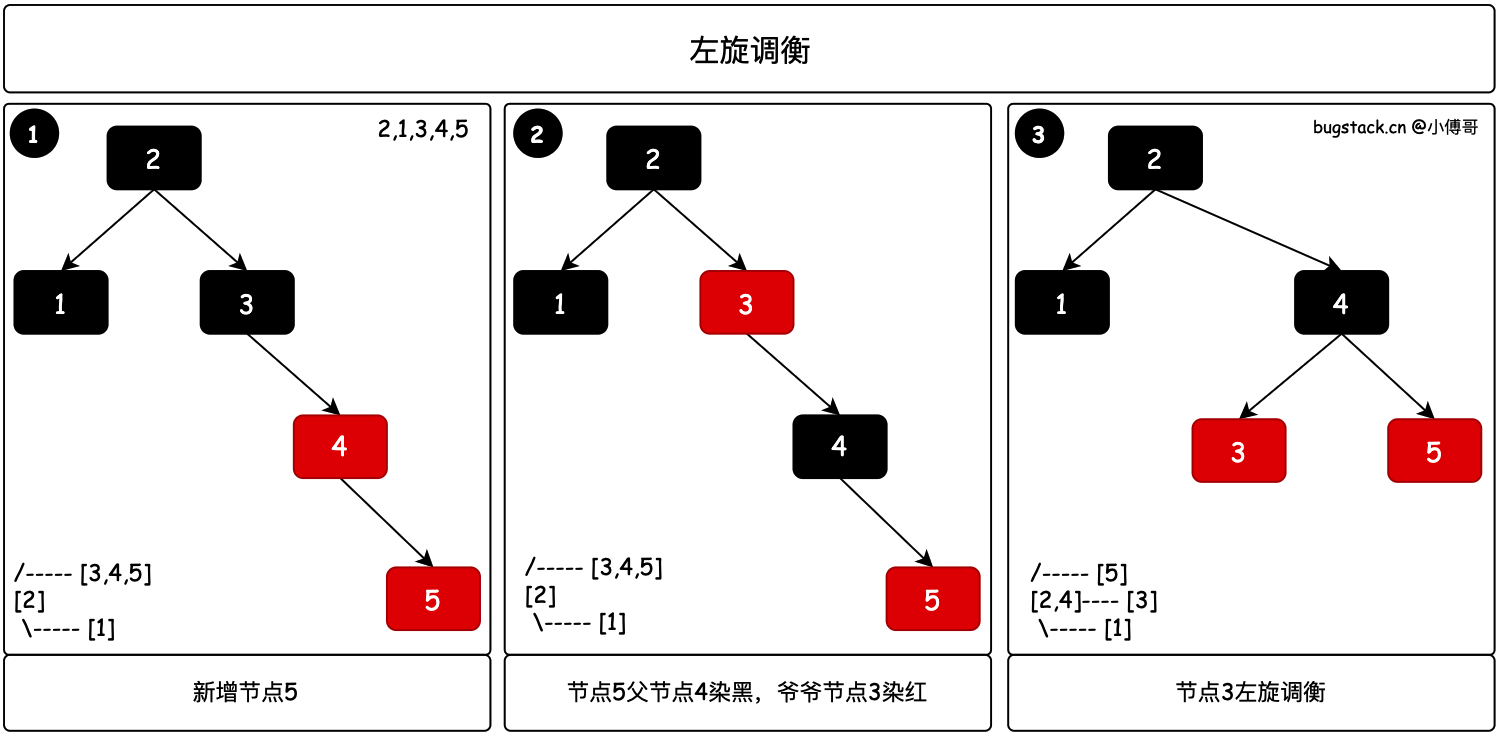
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateLeft(grandParent);
- 當你把紅黑樹對照理解成2-3樹,如圖中第1步驟下的左側小圖,新增的節點5倒置2-3樹不平衡。
- 那麼這個時候需要把2-3樹中節點4提起來,而對應紅黑樹則需要先進行染色,待操作的節點4為黑色,兩個孩子節點為紅色。
- 最後是把節點3進行一次左旋操作,完成樹的平衡。對應步驟3中的左側小圖是2-3樹調衡後的結果。
2.3.2 右旋 + 左旋
當一次左旋沒法調衡,需要右旋+左旋的情況,在AVL樹中有同樣的場景。本身樹需要左旋操作,但整體分支樹節點偏左,此時需要右旋調整樹結構再左旋。此處可參考小傅哥編寫的AVL樹
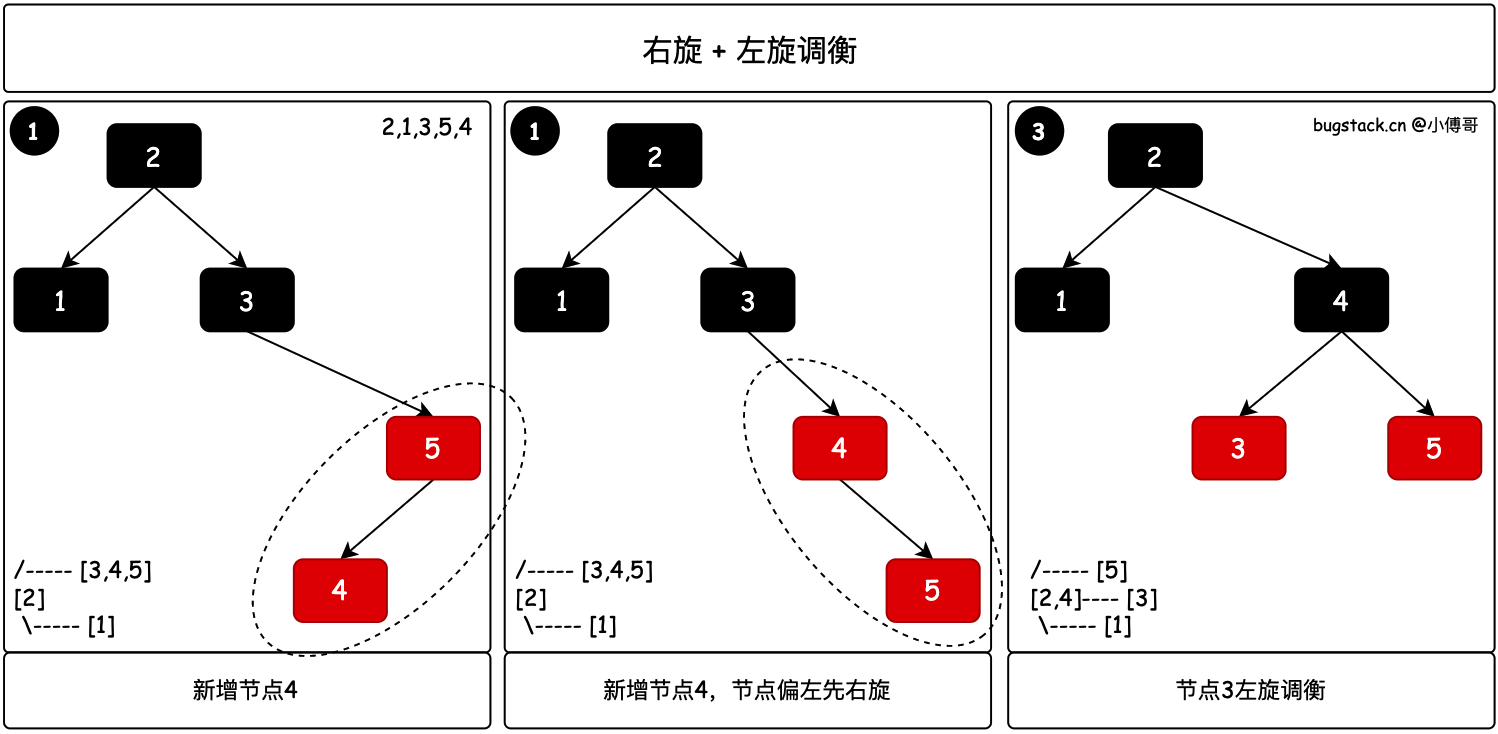
// 偏左↙,先右旋一次調衡
if (current == parent.left){
current = parent;
super.rotateRight(current);
parent = current.parent;
}
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateLeft(grandParent);
- 紅黑樹新增節點4以後,4↙5 結構偏左,需要先進行右旋調衡樹結構,再進行左旋。其實這個時候再進行的左旋就和上面一次左旋操作一致了。
4. 右旋調衡
2.4.1 一次右旋
對照2-3樹,只有當一個節點內有3個節點的時候,才需要調衡。那麼紅黑樹則是判斷當前節點的叔叔節點是否為紅色節點,如果不是則沒法通過染色調衡,也就是需要選擇進行調衡。
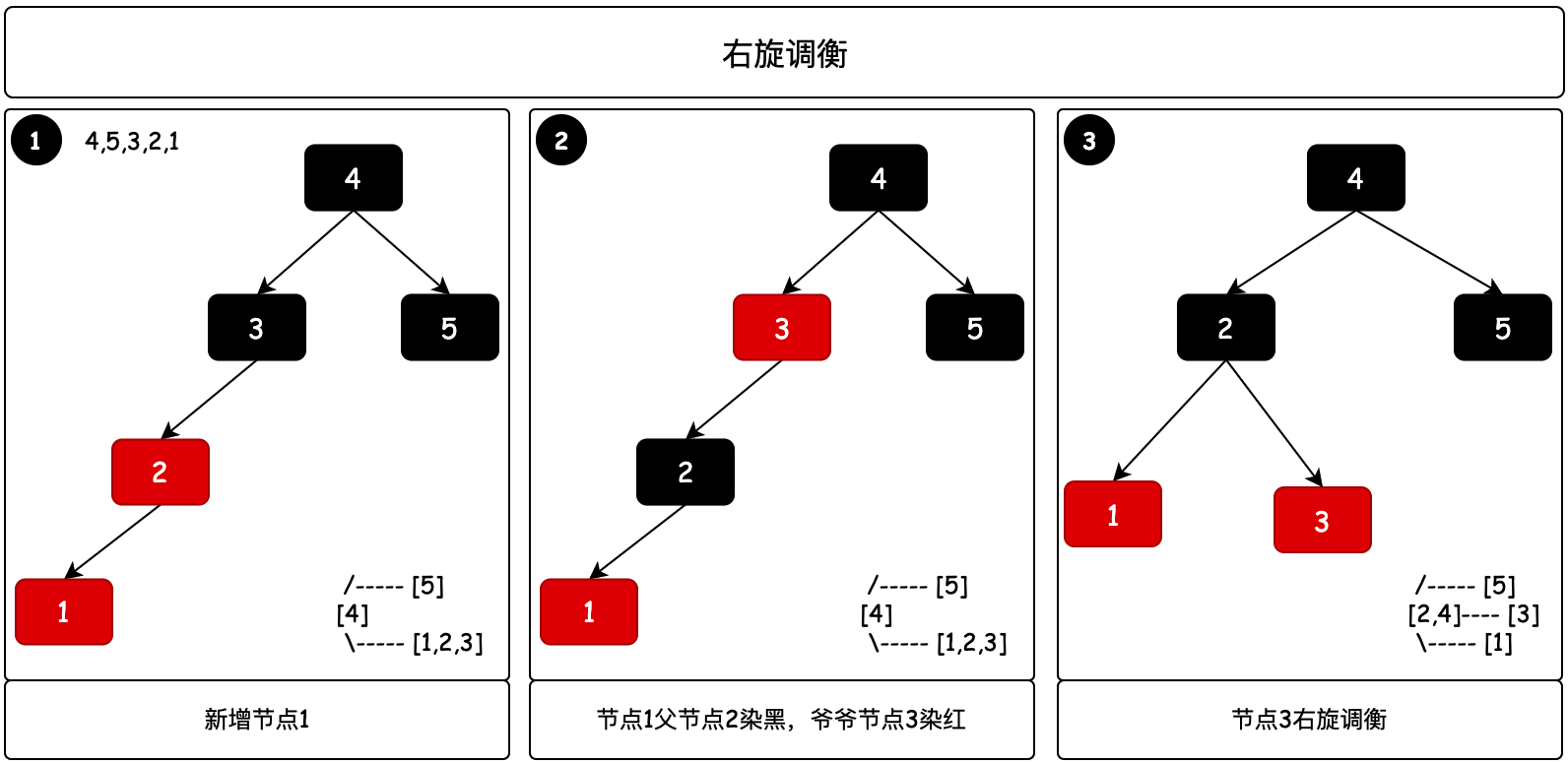
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateRight(grandParent);
- 當你把紅黑樹對照理解成2-3樹,如圖中第1步驟下的右側小圖,新增的節點1倒置2-3樹不平衡。
- 那麼這個時候需要把2-3樹中節點2提起來,而對應紅黑樹則需要先進行染色,待操作的節點2為黑色,兩個孩子節點為紅色。
- 最後是把節點2進行一次右旋操作,完成樹的平衡。對應步驟3中的右側小圖是2-3樹調衡後的結果。
2.4.2 左旋 + 右旋
當一次左旋沒法調衡,需要左旋+右旋的情況,在AVL樹中有同樣的場景。本身樹需要右旋操作,但整體分支樹節點偏右,此時需要左旋調整樹結構再右旋。
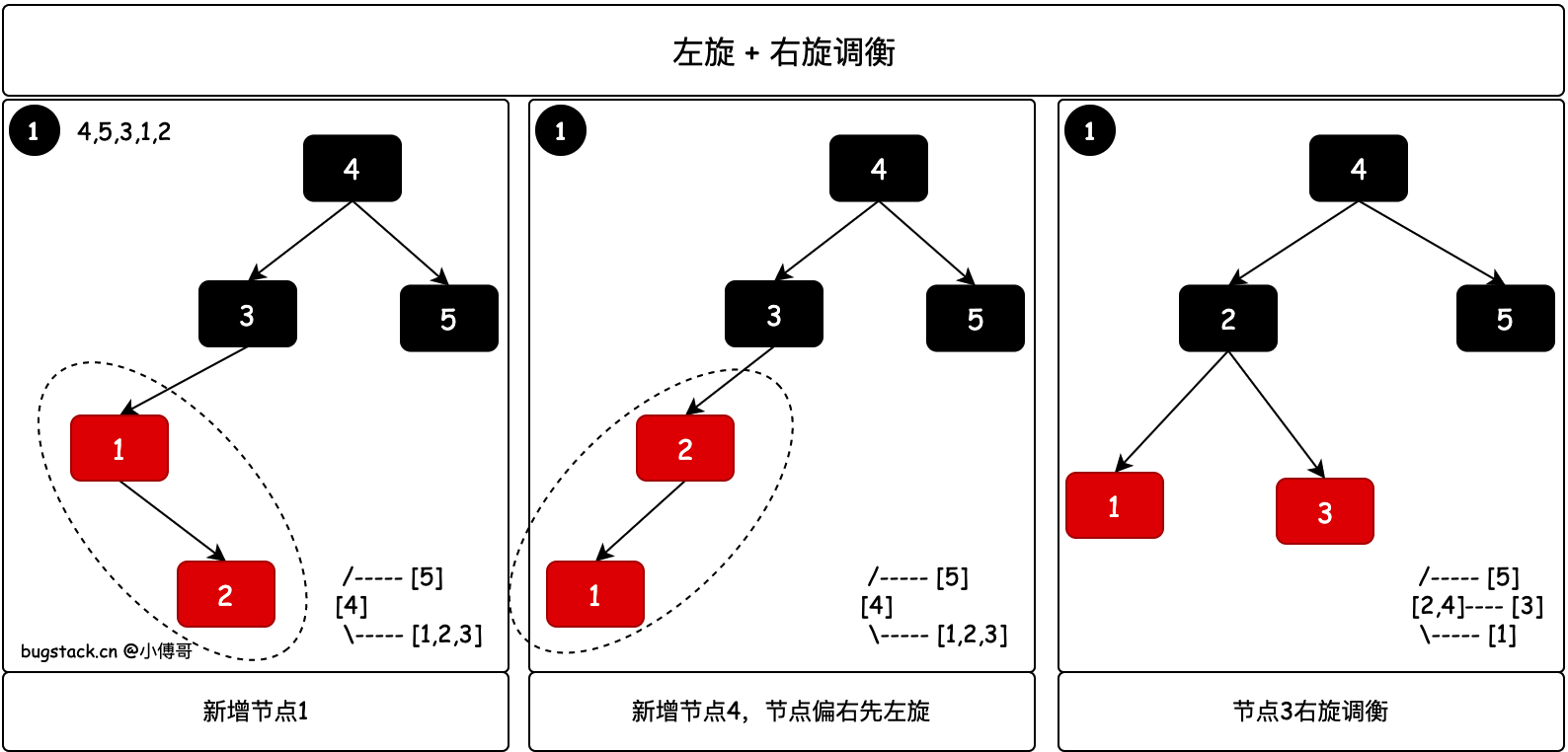
// 偏右↘,先左旋一次調衡
if (current == parent.right){
current = parent;
super.rotateLeft(current);
parent = current.parent;
}
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateRight(grandParent);
- 紅黑樹新增節點2以後,1↘2 結構偏右,需要先進行左旋調衡樹結構,再進行右旋。其實這個時候再進行的右旋就和上面一次右旋操作一致了。
3. 紅黑樹實現測試
為了驗證紅黑樹的實現正確與否,這裡我們做一下隨機節點的插入,如果它能一直保持平衡,那麼它就是一顆可靠紅黑平衡樹。
@Test
public void test_binary_search_tree() {
Tree tree = new RedBlackTree();
for (int i = 0; i < 20; i++) {
tree.insert(new Random().nextInt(100));
}
System.out.println(tree);
}
測試結果
RedBlackTree,輸入節點:79,92,36,35,72,22,11,66,98,28,30,39,56,26,1,25,33,80,22,23
/----- <NIL>
/----- 98(紅)
| \----- <NIL>
/----- 92(黑)
| | /----- <NIL>
| \----- 80(紅)
| \----- <NIL>
/----- 79(黑)
| | /----- <NIL>
| | /----- 72(黑)
| | | \----- <NIL>
| \----- 66(紅)
| | /----- <NIL>
| | /----- 56(紅)
| | | \----- <NIL>
| \----- 39(黑)
| \----- <NIL>
36(黑)
| /----- <NIL>
| /----- 35(黑)
| | | /----- <NIL>
| | \----- 33(紅)
| | \----- <NIL>
| /----- 30(紅)
| | | /----- <NIL>
| | \----- 28(黑)
| | \----- <NIL>
\----- 26(黑)
| /----- <NIL>
| /----- 25(紅)
| | \----- <NIL>
| /----- 23(黑)
| | | /----- <NIL>
| | \----- 22(紅)
| | \----- <NIL>
\----- 22(紅)
| /----- <NIL>
\----- 11(黑)
| /----- <NIL>
\----- 1(紅)
\----- <NIL>
對照2-3樹結構
/----- [98]
/----- [92]
| \----- [80]
/----- [79]
| | /----- [72]
| \----- [66]
| \----- [39,56]
[36]
| /----- [33,35]
| /----- [30]
| | \----- [28]
\----- [26]
|
| /----- [25]
\----- [22,23]----- [22]
\----- [1,11]
- 隨機插入20個節點,每個節點的順序已經打印,經過紅黑樹的染色和左右旋調衡後,二叉結構始終保持樹保持平衡,那麼驗證通過。
- 另外本文出現的案例已經在單元測試中都有編寫,讀者可以在源碼中進行測試。


