第十六周

2 的 n 次冪

• 高精度乘法

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * 2;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    int n;
    cin >> n;
    vector<int> A;
    A.push_back(1);
    while (n--) {
        A = mul(A);
    }
    for (int i = A.size() - 1; i >= 0; i--) {
        printf("%d", A[i]);
    }
    return 0;
}

個數統計

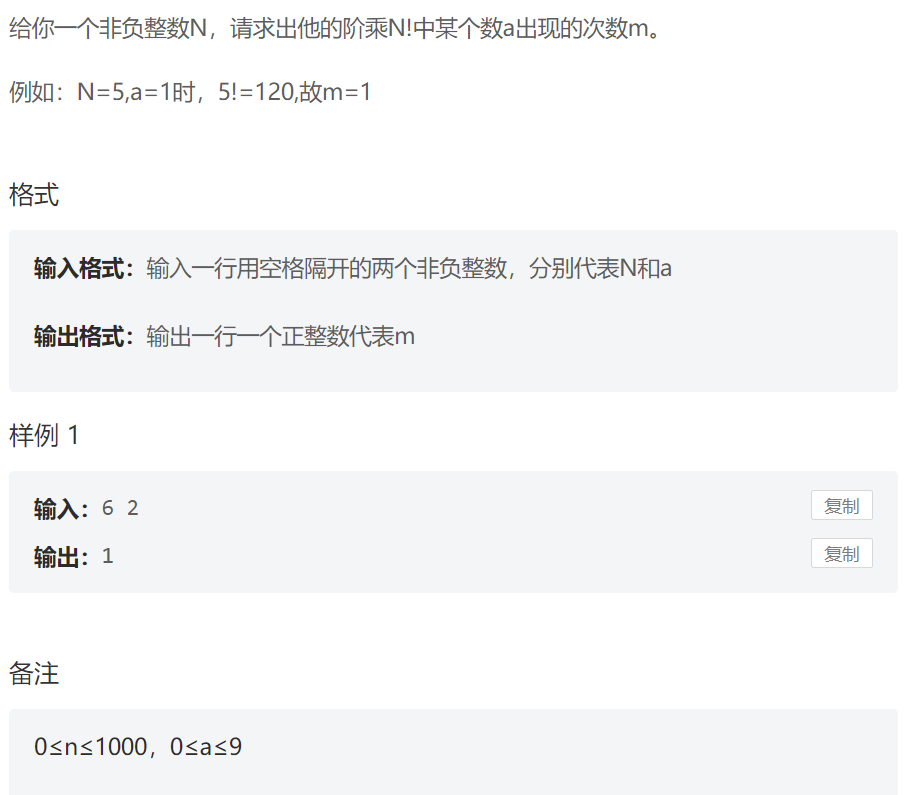
• 高精度乘法求階乘
• 個數統計

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A, int x) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * x;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main( )
{
    int N, a;
    cin >> N >> a;
    vector<int> A;
    A.push_back(1);
    for (int i = 2; i <= N; i++) {
        A = mul(A, i);
    }
    int ans = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        if (A[i] == a) ans++;
    }
    cout << ans << endl;
    return 0;
}

數組扞插

題目複述：

• 將數組分為三部分，前半段，後半段，和中間的數（如果數組大小是奇數）
• 前半段升序排列
• 後半段降序排列
• 如果有中間的數字，則中間的數不參與排列，直接放到結果數組的末尾

#include<bits/stdc++.h> 

using namespace std;

int n;
const int N = 10010;
int a[N], b[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int l = n + 1 >> 1; // 前半段 + 中間數字（可能沒有）
    int r = n - l;      // 後半段
    if (l == r) {       // 前後一樣多
        sort(a, a + l, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    else {              // 前面多一個，則中間的數不參與排序
        sort(a, a + l - 1, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    int ll = 0, rr = l;

    // 交叉插入結果數組
    for (int i = 0; i < n; i++) {
        if (i % 2 == 0) b[i] = a[ll++];
        else b[i] = a[rr++];
    }
    for (int k = 0; k < n; k++) {
        printf("%d ", b[k]);
    }
    return 0;
}

MXR 競賽

題目複述：

• N 個問題，都有積分，範圍為負數、零和正數
• 選出所有一個積分子集，使得子集中的所有積分的乘積得到最大值

解法：

• 貪心思想
• 所有積分從小到大排序，所有正數全部參與乘積
• 所有負數，相鄰兩個負數相乘得到正數。從左向右遍歷，只要相鄰兩個積分是負數，則這兩個負數都參與乘積；最後可能剩下一個絕對值最小的負數，不參與乘積
• 特殊情況：如果所有積分都沒有選取，比如只有一個負數，返回數組最後一個數（最大）

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
long n;
int a[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    long ans = 1;       // 注意精度，int 會爆精度
    int flag = 0;
    sort(a, a + n);
    for (int i = 0; i < n; i++) {
        if (a[i] < 0) {
            if (i < n - 1 && a[i + 1] < 0) {
                ans = ans * (a[i] * a[i + 1]);
                ans %= 998244353;
                i++;
                flag++;
            }
        } else if (a[i] > 0) {
            ans = ans * a[i];
            ans %= 998244353;
            flag++;
        }
    }
    if (flag == 0) printf("%d", a[n - 1]);
    else printf("%d", ans);
    return 0;
}

小碼哥的跳棋遊戲

題目複述：

• 沒有棋子不消耗能量
• 一次最多跳過一個棋子
• 破壞一個棋子消耗一個能量
• 求消耗最小能量從 0 位置到達 n 位置

解法：

• 貪心思想 + 雙指針
• 對於連續 n 個棋子，n 為奇數，最少破壞 ⌊n / 2⌋ 個棋子
• 對於連續 n 個棋子，n 為偶數，最少破壞 n / 2 個棋子
• 由於 int 除法自動取整特性，以上兩種情況可以合併

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
int a[N];

int main( )
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int ans = 0;
    int i = 0;
    while (i < n) {
        // 出現棋子
        if (a[i] == 1) {
            int count = 1;
            int j;
            // 統計連續棋子個數
            for (j = i + 1; j < n && a[j] == 1; j++) {
                 count++;
            }
            ans += count / 2;
            // 破壞之後就可以跳動了
            i = j;
        } else {
            // 沒有棋子就直接跳
            i++;
        }
    }
    // 由於跳動到第 n 塊，如果第 n - 1 塊是棋子，需要破壞
    if (a[n - 1] == 1) ans++;
    cout << ans;
    return 0;
}

矩陣乘法

• 常規矩陣乘法

#include<bits/stdc++.h> 

using namespace std;

const int N = 1010;
int a[N][N], b[N][N], c[N][N];
int l, m, n;
void mul(int a[][N], int b[][N]) {
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            for (int k =0; k < m; k++) {
                c[i][j] += a[i][k] * b[k][j];
            }
        }
    }
}

int main( )
{
    cin >> l >> m >> n;
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &b[i][j]);
        }
    }
    mul(a, b);
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            printf("%d ", c[i][j]);
        }
        printf("\n");
    }
    return 0;
}