矩陣類問題處理技巧
矩陣類問題處理技巧
作者:Grey
原文地址:
給定一個正方形矩陣,原地調整成順時針90度轉動的樣子
題目鏈接見:LeetCode 48. Rotate Image
本題主要的限制條件是:原地調整,即不開闢額外的二維數組來做。
主要思路如下
第一步,先處理外圍的圈 然後同理依次處理每個內圈。
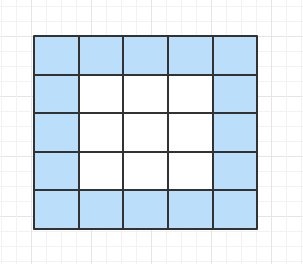
第二步,每個圈分組,組內每次一個元素佔據下一個元素的位置,如果是N*N就分(N-1)*(N-1)個組。如下圖。顏色一樣的就是同一組。
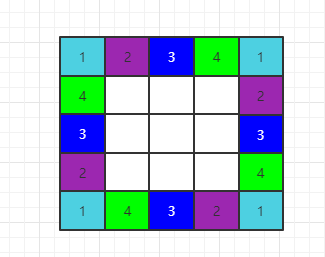
第三步,每個組的每個數可以通過組號來定位。如下圖:

編號一樣的就是同一組,同一組的某個位置,按順時針方向,可以很方便定位到本組下一個位置。
組內調整的核心代碼如下
private static void rotate(int n, int[][] matrix, int zuoshangX, int zuoshangY, int youxiaX, int youxiaY) {
int zu = n - 1;
int youshangX = zuoshangX;
int youshangY = youxiaY;
int zuoxiaX = youxiaX;
int zuoxiaY = zuoshangY;
for (int i = 1; i <= zu; i++) {
// 每組內部調整
int tmp = matrix[zuoshangX][zuoshangY];
matrix[zuoshangX][zuoshangY++] = matrix[zuoxiaX][zuoxiaY];
matrix[zuoxiaX--][zuoxiaY] = matrix[youxiaX][youxiaY];
matrix[youxiaX][youxiaY--] = matrix[youshangX][youshangY];
matrix[youshangX++][youshangY] = tmp;
}
}
完整代碼見
class Solution {
public static void rotate(int[][] matrix) {
int n = matrix.length;
int zuoshangX = 0;
int zuoshangY = 0;
int youxiaX = n - 1;
int youxiaY = n - 1;
while (n > 0) {
// 先處理外圍,然後逐步處理內圈。
rotate(n, matrix, zuoshangX++, zuoshangY++, youxiaX--, youxiaY--);
n -= 2;
}
}
private static void rotate(int n, int[][] matrix, int zuoshangX, int zuoshangY, int youxiaX, int youxiaY) {
int zu = n - 1;
int youshangX = zuoshangX;
int youshangY = youxiaY;
int zuoxiaX = youxiaX;
int zuoxiaY = zuoshangY;
for (int i = 1; i <= zu; i++) {
// 每組內部調整
int tmp = matrix[zuoshangX][zuoshangY];
matrix[zuoshangX][zuoshangY++] = matrix[zuoxiaX][zuoxiaY];
matrix[zuoxiaX--][zuoxiaY] = matrix[youxiaX][youxiaY];
matrix[youxiaX][youxiaY--] = matrix[youshangX][youshangY];
matrix[youshangX++][youshangY] = tmp;
}
}
}
給定一個長方形矩陣,實現轉圈打印
和上一題類似,先打印外圍圈圈,然後切換到內圈,用同樣的方式打印內圈,依次循環。
打印的時候,我們只需要定位左上和右下兩個點的坐標位置即可確定一個矩形。
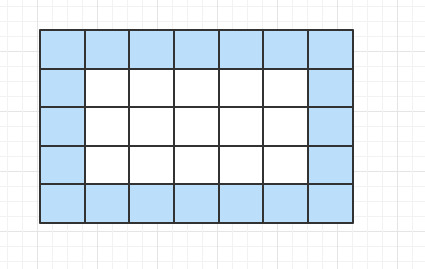
需要注意的是,最後有可能是一條直線,比如下述兩種情況中的標紅位置
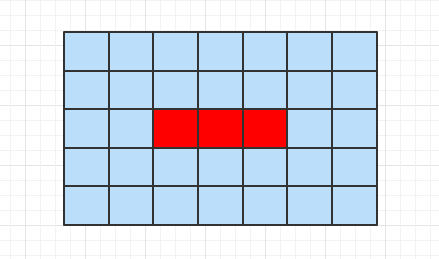
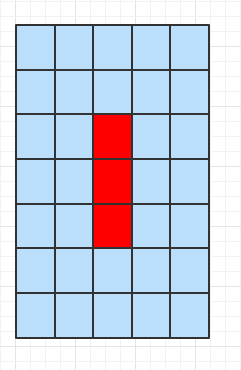
對於形成一條直線的情況,單獨處理並打印即可。
完整代碼見
class Solution {
public static List<Integer> spiralOrder(int[][] matrix) {
if (null == matrix || matrix.length == 0 || matrix[0].length == 0) {
return new ArrayList<>();
}
int m = matrix.length;
int n = matrix[0].length;
// 左上角點
int a = 0, b = 0;
// 右下角點
int c = m - 1, d = n - 1;
List<Integer> ans = new ArrayList<>();
while (a <= c && b <= d) {
spiral(matrix, a++, b++, c--, d--, ans);
}
return ans;
}
public static void spiral(int[][] matrix, int a, int b, int c, int d, List<Integer> ans) {
if (a == c) {
// 形成一條直線:共行
for (int i = b; i <= d; i++) {
ans.add(matrix[a][i]);
}
return;
}
if (b == d) {
// 形成一條直線:共列
for (int i = a; i <= c; i++) {
ans.add(matrix[i][b]);
}
return;
}
for (int i = b; i < d; i++) {
ans.add(matrix[a][i]);
}
for (int i = a; i < c; i++) {
ans.add(matrix[i][d]);
}
for (int i = d; i > b; i--) {
ans.add(matrix[c][i]);
}
for (int i = c; i > a; i--) {
ans.add(matrix[i][b]);
}
}
}
zigzag打印矩陣
題目描述見:LintCode 185 · Matrix Zigzag Traversal
zigzag 方式如下
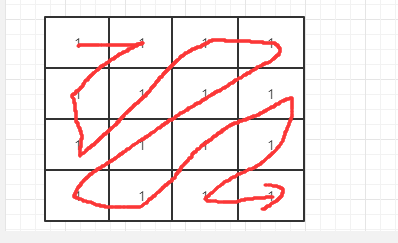
本題的主要思路是
從左上角的開始位置,準備兩個變量 A 和 B,A 往左邊走,走到不能再走的時候,往下走
B 往下走,走到不能再往下的時候,往左邊走,每次 AB 構成的連線進行打印(方向交替變化)
完整代碼見:
public class Solution {
/**
* @param matrix: An array of integers
* @return: An array of integers
*/
public static int[] printZMatrix(int[][] matrix) {
if (null == matrix || matrix.length == 0 || matrix[0].length == 0) {
return null;
}
int m = matrix.length;
int n = matrix[0].length;
int[] ans = new int[m * n];
ans[0] = matrix[0][0];
// 右邊-->下邊
int a = 0, b = 0;
// 下邊-->右邊
int c = 0, d = 0;
int index = 1;
boolean topToDown = true;
for (int k = 0; k < m + n; k++) {
if (b < n - 1) {
b++;
} else if (b == n - 1) {
a++;
}
if (c < m - 1) {
c++;
} else if (c == m - 1) {
d++;
}
if (topToDown) {
int j = b;
for (int i = a; i <= c; i++) {
ans[index++] = matrix[i][j--];
}
} else {
int j = d;
for (int i = c; i >= a; i--) {
ans[index++] = matrix[i][j++];
}
}
topToDown = !topToDown;
}
return ans;
}
}
螺旋打印星號
依舊是先處理外圈,然後依次內圈的處理方式,
完整代碼見
package snippet;
// 螺旋打印星號
public class Code_0093_PrintStar {
public static void printStar(int N) {
int leftUp = 0;
int rightDown = N - 1;
char[][] m = new char[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
m[i][j] = ' ';
}
}
while (leftUp <= rightDown) {
set(m, leftUp, rightDown);
leftUp += 2;
rightDown -= 2;
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(m[i][j] + " ");
}
System.out.println();
}
}
public static void set(char[][] m, int leftUp, int rightDown) {
for (int col = leftUp; col <= rightDown; col++) {
m[leftUp][col] = '*';
}
for (int row = leftUp + 1; row <= rightDown; row++) {
m[row][rightDown] = '*';
}
for (int col = rightDown - 1; col > leftUp; col--) {
m[rightDown][col] = '*';
}
for (int row = rightDown - 1; row > leftUp + 1; row--) {
m[row][leftUp + 1] = '*';
}
}
public static void main(String[] args) {
printStar(5);
}
}
打印結果如下
* * * * *
*
* * *
* *
* * * *