論文解讀（NWR）《Graph Auto-Encoder via Neighborhood Wasserstein Reconstruction》

• 2022 年 8 月 20 日
• 筆記
• 論文解讀

論文信息

論文標題：Graph Auto-Encoder via Neighborhood Wasserstein Reconstruction
論文作者：Shaked Brody, Uri Alon, Eran Yahav
論文來源：2022,ICLR
論文地址：download 
論文代碼：download

1 Abstract

　　圖神經網絡(GNNs)近年來引起了廣泛的研究關注，主要是在半監督學習的背景下。當任務不可知的表示是首選或監督完全不可用時，自動編碼器框架與無監督GNN訓練的自然圖重建目標一起使用。然而，現有的圖自動編碼器是通過設計來重建直接鏈路的，因此以這種方式訓練的gnn只針對面向鄰近的圖挖掘任務進行優化，當拓撲結構很重要時就會失敗。在本研究中，我們重新討論了gnn的圖編碼過程，它本質上學習了將每個節點的鄰域信息編碼為一個嵌入向量，並提出了一種新的圖解碼器，通過鄰域瓦瑟斯坦重建(NWR)來重建關於鄰近性和結構的整個鄰域信息。

　　具體來說，NWR從每個節點的GNN嵌入中，聯合預測其節點度和鄰居特徵分佈，其中分佈預測採用了基於瓦瑟斯坦距離的最優傳輸損失。在合成網絡數據集和真實網絡數據集上的大量實驗表明，使用NWR學習的無監督節點表示在面向結構的圖挖掘任務中具有更大的優勢，同時在面向接近的圖挖掘任務中也具有競爭性能。

2 Introduction

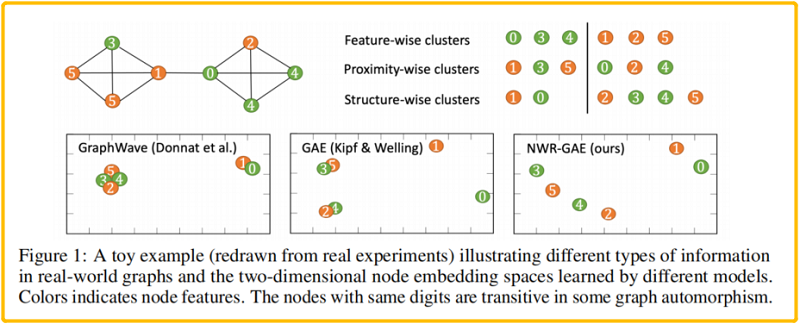
　　現有的圖自動編碼：

• • 例如 GAE（Kipf & Welling, 2016）學習的節點表示由於其優化簡單的重建目標以至無法區分像 (2, 4) 和 (3, 5)這樣的點；
  • 例如  GraphWave (Donnat et al., 2018) 這樣的面向結構的嵌入模型不考慮節點特徵和空間接近度，無法區分像 (0, 1), (2, 4) 和 (3，5) 這樣的節點對；

　　具體地說，本文將解碼過程描述為從通過 GNN 編碼器獲得的多跳鄰居表示上定義的一系列概率分佈中進行迭代採樣。然後，將重構損失分解為三個部分，即採樣數（節點度）、鄰居表示分佈和節點特徵。本文最重要的術語是「 鄰居表示分佈重建」（neighborrepresentation distribution reconstruction），本文採用了基於 Wasserstein distance 的最優傳輸損失，因此將這個新的框架命名為 Neighborhood Wasserstein Reconstruction Graph Auto-Encoder (NWR-GAE).。如 Figure1 所示，NWR-GAE可以有效地在不同的角度區分所有不同的節點對，並簡明地反映出它們在低維嵌入空間中的相似性。

　　為了更好地理解這一點，我們仔細分析了通過GNN在每個節點表示中編碼的信息源。假設採用一個標準的消息傳遞 GNN (Gilmer等人，2017) 作為編碼器，這是一個通用框架，包括 GCN 、GraphSAGE、GAT、GIN 等等。在 k-hop 消息傳遞後，在節點 $v$ 的表示中編碼的信息來源本質上來自於 $v$ 的 $k-hop$ 鄰域（Fig.2）。因此，節點 $v$ 的良好表示應該捕獲其 $k$ 跳鄰域中所有節點的特徵信息，這與下游任務是無關的。請注意，這可能不是理想的，因為 $k-hop$ 鄰域外的節點也可能提供有用的信息，但由於 GNN 編碼器的架構，這是基於 GNN 的圖自動編碼器可以期望做的。這一觀察結果促使我們研究了一種新的圖解碼器，該解碼器可以更好地促進基於 GNN 的圖自動編碼器的目標。我們將在 Sec3 中正式確立這一原則。

　　最近，DGI、EGI 在無監督GNN訓練方法中使用了對比學習，並可能捕獲定向鏈接之外的信息。它們採用了互信息最大化規則 (InfoMax)，它本質上是為了最大化學習到的表示和原始數據之間的某些對應關係。例如，DGI 最大化了節點表示與節點所屬的圖之間的對應關係，但這並不能保證重建節點鄰域的結構信息。最近的研究甚至表明，最大化這種對應關係可能只捕獲與下行任務無關的噪聲信息，因為噪聲信息本身足以讓模型實現 InfoMax，我們的實驗再次證明了這一點。相反，我們的目標是讓節點表示不僅捕獲信息來區分節點，而且捕獲儘可能多的信息來重建鄰域的特徵和結構。

　　許多機器學習問題依賴於兩個概率測度量之間的距離的描述。當兩個分佈有非重疊的部分時，$f$ 散度存在非連續的問題。

　　Suppose we have two probability distributions, $P$ and $Q$ :

　　$\forall(x, y) \in P, x=0 \text { and } y \sim U(0,1) \forall(x, y) \in Q, x=\theta, 0 \leq \theta \leq 1 \text { and } y \sim U(0,1)$

　　

　　When $\theta \neq 0$ ：

　　　　$D_{K L}(P \| Q) =\sum\limits _{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty$
　　　　$D_{K L}(Q \| P) =\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty$
　　　　$D_{J S}(P, Q) =\frac{1}{2}\left(\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}+\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}\right)=\log 2$
　　　　$W(P, Q) =|\theta| $

　　But when $\theta = 0$, two distributions are fully overlapped:

　　　　$D_{K L}(P \| Q) =D_{K L}(Q \| P)=D_{J S}(P, Q)=0$

　　　　$W(P, Q) =0=|\theta|$

　　因此，OT 損失經常被採用，並在生成模型和領域適應中取得了巨大的成功。OT 損失已被用於構建非圖形數據的變分自動編碼器。但應該注意的是，我們的工作並不是這些工作的面向圖數據的泛化：他們使用 OT 損失來描述變分分佈和數據經驗分佈之間的距離，而我們的模型甚至不使用變分分佈。我們的模型可以進一步改進為一個變分自編碼器，但我們把它作為一個未來的方向。

　　在這裡，我們給出了一個基於 2-Wasserstein distance 的常用的 OT 損失，這將在稍後使用。

　　Definition 2.1. Let $\mathcal{P}$, $\mathcal{Q}$ denote two probability distributions with finite second moment defined on $\mathcal{Z} \subseteq \mathbb{R}^{m}$ . The 2-Wasserstein distance between $\mathcal{P}$ and $\mathcal{Q}$ defined on $\mathcal{Z}$, $\mathcal{Z}^{\prime} \subseteq \mathbb{R}^{m}$ is the solution to the optimal mass transportation problem with $\ell_{2}$ transport cost (Villani, 2008):

　　　　$\mathcal{W}_{2}(\mathcal{P}, \mathcal{Q})=\left(\inf _{\gamma \in \Gamma(\mathcal{P}, \mathcal{Q})} \int_{\mathcal{Z} \times \mathcal{Z}^{\prime}}\left\|Z-Z^{\prime}\right\|_{2}^{2} d \gamma\left(Z, Z^{\prime}\right)\right)^{1 / 2}$

　　where $\Gamma(\mathcal{P}, \mathcal{Q})$ contains all joint distributions of $\left(Z, Z^{\prime}\right)$ with marginals $\mathcal{P}$ and $\mathcal{Q}$ respectively.

3 Methods

　　預先定義 ：

• • Encoder：$\phi$
  • Decoder：$\psi$

　　Encoder 可以是任何基於消息傳遞的 GNNs，Decoder 可以分成三部分：$\psi=\left(\psi_{s}, \psi_{p}, \psi_{d}\right)$

3.1 Neighborhood peconstruction principle

　　為了簡化闡述，我們從 1 跳鄰域重建開始。我們基於 $X$ 用 $H^{(0)}$ 初始化節點表示。對於每個節點 $v \in V$，在被一個GNN層編碼後，其節點表示h $h_{v}^{(1)}$ 從 $h_{v}^{(0)}$ 及其鄰居的表示 $H_{\mathcal{N}_{v}}^{(0)}=\left\{h_{u}^{(0)} \mid u \in \mathcal{N}_{v}\right\}$ 中收集信息。因此，我們考慮以下原則，即重構來自 $h_{v}^{(0)}$ 和 $H_{\mathcal{N}_{v}}^{(0)}$ 的信息。因此，我們有了

　　　　$\begin{array}  {l}\underset{\phi, \psi}{\text{min}} &   \sum\limits _{v \in V} \mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}^{(1)}\right)\right)\\\text { s.t. } & h_{v}^{(1)}=\phi\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \forall v \in V\end{array} \quad\quad\quad(2)$

　　式中，$\mathcal{M}(\cdot, \cdot)$ 定義了重建損失。$M$ 可以分為兩部分，分別測量自特徵重建和鄰域重建：

　　　　$\mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}^{(1)}\right)\right)=\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)+\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)\quad\quad\quad(3)$

　　請注意，$\mathcal{M}_{s}$ 的工作原理就像一個基於標準的前饋神經網絡(FNN)的自動編碼器的重建損失一樣，所以我們採用了

　　　　$\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)=\left\|h_{v}^{(0)}-\psi_{s}\left(h_{v}^{(1)}\right)\right\|^{2}\quad\quad\quad(4)$

　　$\mathcal{M}_{n}$ 很難被描述，因為它測量的是重建一組特徵 $H_{\mathcal{N}_{v}}^{(0)}$ 的損失。有兩個基本的挑戰：首先，在現實網絡中，節點度的分佈通常是長尾的，節點鄰居的集合可能有非常不同的大小。其次，為了比較甚至兩個大小相等的集合，也必須解決一個匹配問題，因為可以假定集合中沒有固定的元素順序。如果集合的大小較大，則解決匹配問題的複雜性很高。我們通過將鄰域信息解耦為概率分佈和採樣數來解決上述挑戰。具體來說，對於節點 $v$，鄰域信息被表示為 i.i.d .的經驗實現從 $\mathcal{P}_{v}^{(0)}$ 中採樣 $d_{v}$ 元素，其中 $\mathcal{P}_{v}^{(0)} \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(0)}}$。基於這一觀點，我們可以將重建分別分解為節點度和分佈的部分，其中不同大小的節點鄰域得到了正確的處理。具體來說，我們採用

　　　　$\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)=\left(d_{v}-\psi_{d}\left(h_{v}^{(1)}\right)\right)^{2}+\mathcal{W}_{2}^{2}\left(\mathcal{P}_{v}^{(0)}, \psi_{p}^{(1)}\left(h_{v}^{(1)}\right)\right)\quad\quad\quad(5)$

Generalizing to k-hop neighborhood reconstruction

　　根據上述對第一個情況的推導，我們可以類似地推廣基於 $h_{v}^{(i)}$ 的重構 $\left(h_{v}^{(i-1)}, H_{\mathcal{N}_{v}}^{(i-1)}\right)$ 的損失。然後，如果我們將所有節點 $v \in V$ 和所有跳 $1 \leq i \leq k$ 的損失相加，我們可以實現 $k$ 跳鄰域重建的目標。我們可以進一步簡化這一目標。通常，只有最終的層表示 $H^{(k)}$ 被用作輸出降維表示。過多的中間跳使模型難以訓練，收斂速度慢。因此，我們採用了一種更經濟的方式，合併了多步重建：

　　也就是說，我們期望 $h_{v}^{(k)}$ 直接重構 $H_{\mathcal{N}_{v}}^{(i)}$，即使 $i<k-1$。具體來說，對於每個節點 $v \in V$，我們使用重構損失

　　$\begin{array}{l}&\mathcal{M}^{\prime}\left(\left(h_{v}^{(0)},\left\{H_{\mathcal{N}_{v}}^{(i)} \mid 0 \leq i \leq k-1\right\}\right), \psi\left(h_{v}^{(k)}\right)\right)=\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(k)}\right)\right)+\sum\limits_{i=0}^{k-1} \mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(i)}, \psi\left(h_{v}^{(k)}\right)\right) \\&=\lambda_{s}\left\|h_{v}^{(0)}-\psi_{s}\left(h_{v}^{(k)}\right)\right\|^{2}+\lambda_{d}\left(d_{v}-\psi_{d}\left(h_{v}^{(k)}\right)\right)^{2}+\sum\limits_{i=0}^{k-1} \mathcal{W}_{2}^{2}\left(\mathcal{P}_{v}^{(i)}, \psi_{p}^{(i)}\left(h_{v}^{(k)}\right)\right)\end{array}\quad(6)$

　　其中 $\psi_{s}$ 是解碼初始特徵，$\psi_{d}$ 是度解碼，$\psi_{p}^{(i)}$，$0 \leq i \leq k-1$ 是解碼 $i$ 層鄰域表示分佈 $\mathcal{P}_{v}^{(i)}\left(: \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(i)}}\right)$。$\lambda_{s}$ 和 $\lambda_{d}$ 為非負性超參數。因此，$k$ 跳鄰域重建的全部目標是

　　　　$\begin{array}{l} \underset{\phi, \psi}{\text{min}}\quad \sum\limits _{v \in V} \mathcal{M}^{\prime}\left(\left(h_{v}^{(0)},\left\{H_{\mathcal{N}_{v}}^{(i-1)} \mid 1 \leq i \leq k\right\}\right), \psi\left(h_{v}^{(k)}\right)\right)\\ \text { s.t. }\quad H^{(i)}=\phi^{(i)}\left(H^{(i-1)}\right), \quad1 \leq i \leq k\end{array}$

　　其中，$\phi=\left\{\phi^{(i)} \mid 1 \leq i \leq k\right\}$ 包括 $k$ 個GNN層，$\mathcal{M}^{\prime}$ 在 $\text{Eq.6}$ 中定義。

　　在 $\text{Eq.6}$ 中的損失並不直接推動 $k$ 層表示 $h_{v}^{(k)}$ 來重建所有直接鄰居節點的特徵，但它們位於 $v$ 的 $k$ 跳鄰域。但是，根據定義，在這個 $k$ 跳鄰域中存在一條長度不大於 $k$ 的最短路徑。因為沿路徑的每兩個相鄰節點將引入至少一項等式之和的重建損失。這就保證了在 $\text{Eq.7}$ 中的優化推動 $h_{v}^{(k)}$ 來重建 $v$ 的整個 $k-hop$ 鄰域。

3.2 Decoding distributions——Decoders $\psi_{p}^{(i)}, 0 \leq i \leq k-1$

　　我們的 NRP 本質上是將節點鄰域 $H_{\mathcal{N}_{v}}^{(i)}$ 表示為一個採樣數(節點度 $d_v$ )加上一個鄰居表示 $\mathcal{P}_{v}^{(i)}$ 的分佈($\text{Eq.5.6}$)。我們採用 Wasserstein distance 來表徵分佈重構損失，因為 $\mathcal{P}_{v}^{(i)}$ 在連續空間中具有原子非零測度支持，在連續空間中不能應用 $f$ 散度族的分佈重構損失。可以應用最大平均差異，但它需要指定一個核函數。

　　　　$\begin{array}{l}\psi_{p}^{(i)}\left(h_{v}^{(k)}\right)=\operatorname{FNN}_{p}^{(i)}(\xi),\quad \xi \sim \mathcal{N}\left(\mu_{v}, \Sigma_{v}\right)\\\text { where }\quad \mu_{v}=\operatorname{FNN}_{\mu}\left(h_{v}^{(k)}\right), \quad\Sigma_{v}=\operatorname{diag}\left(\exp \left(\operatorname{FNN}_{\sigma}\left(h_{v}^{(k)}\right)\right)\right)\end{array}$

　　Theorem 3.1. For any  $\epsilon>0$ , if the support of the distribution  $\mathcal{P}_{v}^{(i)}$  lies in a bounded space of  $\mathbb{R}^{m}$ , there exists a $FNN  u(\cdot): \mathbb{R}^{m} \rightarrow \mathbb{R}$  (and thus its gradient  $\nabla u(\cdot): \mathbb{R}^{m} \rightarrow \mathbb{R}^{m}$  ) with large enough width and depth (depending on  $\epsilon$  ) such that  $\mathcal{W}_{2}^{2}\left(\mathcal{P}_{v}^{(i)}, \nabla u(\mathcal{G})\right)<\epsilon$  where  $\nabla u(\mathcal{G})$  is the distribution generated via the mapping  $\nabla u(\xi)$, $\xi \sim  a$  $m$-dim non-degenerate Gaussian distribution.

　　上述損失的計算是基於求解一個匹配問題，需要具有 $O(q^3)$ 複雜度的匈牙利算法。可以採用更有效的替代損失類型，如基於貪婪近似的倒角損失(Fanetal.，2017)或基於連續鬆弛的辛角損失(Cuturi，2013)，其複雜性為 $O(q^2)$。在我們的實驗中，由於 $q$ 是固定為一個小常數，比如5，我們使用等式8基於匈牙利匹配，不引入太多的計算開銷。雖然沒有直接相關，但我們想強調一些最近的工作，即使用 OT 損失作為兩個圖之間的距離，其中採用了這兩個圖的兩組節點嵌入之間的瓦瑟斯坦距離(Xuetal.，2019a；b)。借用這樣一個概念，我們可以查看我們的 OT 損失也來測量原始圖和解碼圖之間的距離。

3.3 Further discussion-Decoders $\psi_{s}$ and $\psi_{d}$

　　重構初始特徵 $h_{v}^{(0)}$ 的解碼器 $\psi_{s}$ 是一個 FNN。重構節點度的解碼器 $\psi_{d}$ 是一個 FNN+指數神經元，使其值非負。

　　　　$\begin{array}{l}\psi_{s}\left(h_{v}^{(k)}\right)&=&\mathrm{FNN}_{s}\left(h_{v}^{(k)}\right)\\\psi_{d}\left(h_{v}^{(k)}\right)&=&\exp \left(\mathrm{FNN}_{d}\left(h_{v}^{(k)}\right)\right)\end{array}\quad\quad\quad(9)$

　　在實際應用中，原始的節點特徵 $X$ 可以是非常高維的，直接重構它們可能會在節點表示中引入大量的噪聲。相反，我們可以首先將 $X$ 映射到一個潛在的空間來初始化 $H^{0}$。然而，如果 $H^{0}$ 同時用於表示學習和重建，它就有崩潰到平凡點的風險。因此，我們通過對範數對 $H^{0}$ 進行適當的歸一化，以避免以下陷阱

　　　　$\begin{array}{l}\left\{h_{v}^{(0)} \mid v \in V\right\}=\text { pair-norm }\left(\left\{x_{v} W \mid v \in V\right\}\right) \\ \text {where } W \text { is a learnable parameter matrix. }\end{array}\quad\quad\quad(10)$

4 Experiments

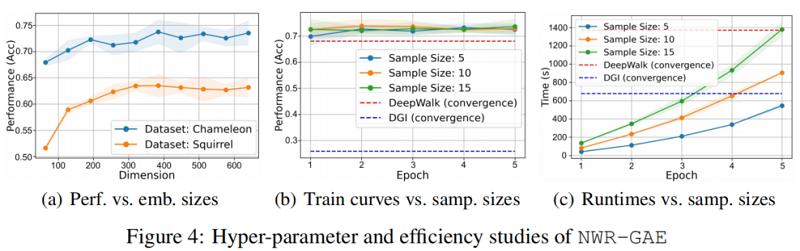
 　　我們設計實驗來評估 NWR-GAE，重點關注以下研究問題：RQ1：與最先進的無監督圖嵌入基線相比，NWR-GAE在基於結構角色的合成數據集上表現如何？RQ2：NWR-GAE及其消融如何與不同類型的真實世界圖形數據集上的基線進行比較？RQ3：嵌入尺寸 $d$ 和採樣尺寸 $q$ 等主要模型參數對NWR-GAE的影響是什麼？

4.1 Experimental setup

4.1.1 Datasets

　　Synthetic datasets

4.1.2 Baselines

　　1) Random walk based (DeepWalk, node2vec)
　　2) Structural role based (RoleX, struc2vec, GraphWave)
　　3) Graph auto-encoder based (GAE, VGAE, ARGVA)
　　4) Contrastive learning based (DGI, GraphCL, MVGRL)

4.1.3 Evaluation metrics

• Homogeneity: conditional entropy of ground-truth among predicting clusters.
• Completeness: ratio of nodes with the same ground-truth labels assigned to the same cluster.
• Silhouette score: intra-cluster distance vs. inter-cluster distance.

4.2 Performance on synthetic datasets(RQ1)

　　

4.3 Performance on real-world datasets(RQ2)

　　

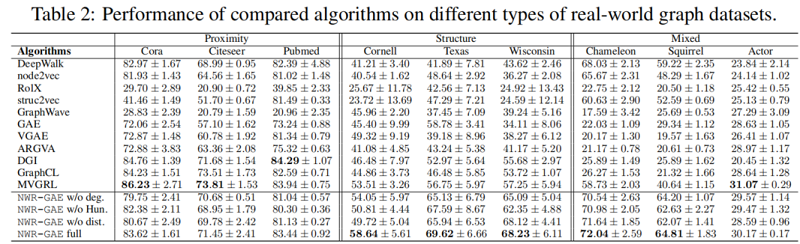
4.4 In-depth analysis of NWR-GAE

5 Conclusion

　　在這項工作中，我們解決了現有的無監督圖表示方法的局限性，並提出了第一個能夠正確地捕獲圖中節點的接近性、結構和特徵信息的模型，並在低維嵌入空間中對其進行區分編碼的模型。該模型在合成和真實基準數據集上進行了廣泛的測試，結果有力地支持了其聲稱的優勢。由於它是通用的，有效的，而且在概念上也很容易理解，我們相信它有潛力作為無監督圖表示學習的實際方法。在未來，它將有望看到其在不同領域的應用研究，以及仔細分析其魯棒性和隱私性等潛在問題。