B+樹索引頁大小是如何確定的?
B+樹簡介
在正式介紹本文的主題前,需要對 B+ 樹有一定的了解,B+樹是一種磁盤上數據的索引結構,大概長這個樣子。
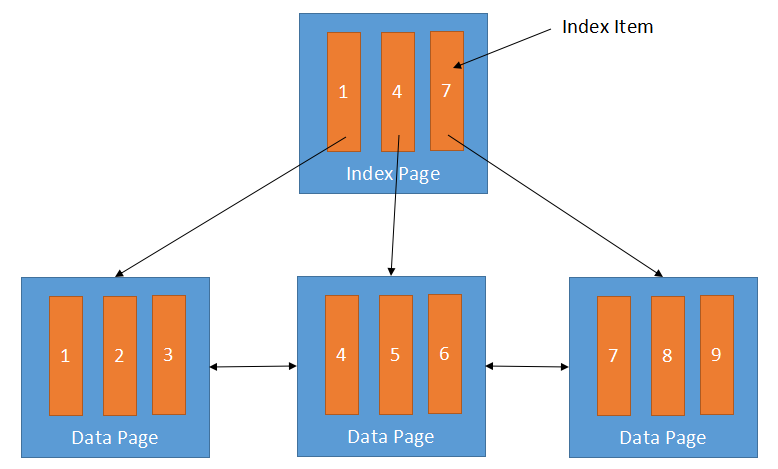
B+樹的葉子節點是所有的數據,非葉子節點稱為索引頁,索引頁里有若干個索引項,本例中有 3 個索引項,也就是索引頁的出度為 3,表示它有 3 個子節點。
相要尋找某一個數據時,比如值為 6 的數據,只需要先在索引頁中找到小於 6 的最大的索引項 4,就可以索引到保存了 4,5,6 三條數據的數據頁,進而找到值為 6 的這一條數據。
當然,B+ 樹不是只有一個索引節點,只是為了方便展示所以圖中只有一個索引節點,一個更大的 B+ 樹如下圖所示。
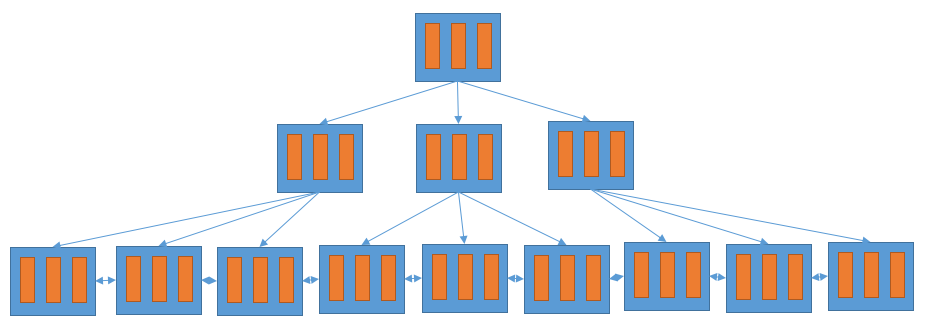
數學推導
假設 B+ 樹總共索引了 N 條數據(葉子節點的數據量),每個索引頁的出度為 EntriesPerPage(索引頁內有多少個索引項),則 B+ 樹的高度可以由如下式子計算:
\]
定義 IndexPageUtility 為衡量索引頁到數據頁的遠近的指標,可以由如下式子計算:
\]
這裡可以不必糾結為什麼 utility 就是這麼算的,只要理解 utility 和 EntriesPerPage 是正相關的關係就可以,因為最後算的收益成本比率只是一個比值,能比較出大小就可以,所以這裡就取 utility 為 IndexHeight 計算公式的分母。
舉個例子,如果索引項大小為 20 位元組,那麼 2KB 的索引頁應該是能裝下 100 個索引項,但實際上索引頁內不僅僅只存有索引項,實際索引項最高能佔用 70% 的空間,也就是 70 個索引項。這樣的索引頁的 utility 為 \(log_{2}{70}\) 約為 6.2,大約是 128KB 大小索引頁 utility 的一半。
每一次讀索引頁都需要讀一次磁盤,相應的距離目標數據也更進一步(使用 utility 衡量步長)。基於這種成本效益的權衡,產生了一個最佳的頁面大小,平衡了讀一次索引頁的收益(IndexPageUtility)和成本(IndexPageAccessCost)。
對於越大的索引頁,它的出度越大,utility 越高,從磁盤讀取的成本也越高,對於特定的磁盤的尋址時間和傳輸速率,有一個最優的索引頁大小。
假設磁盤平均尋址時間為 10 毫秒,傳輸速率為 10MB 每秒,索引頁大小為 2KB,那麼讀取索引頁需要的時間為 10.2 毫秒。
更準確的說,讀取索引頁的成本要麼是有頁面緩存時的內存存儲成本,要麼是從磁盤讀取頁面的磁盤訪問成本。如果根索引頁及附近的索引頁緩存在內存中,能夠節省一個數量恆定的 IO 次數,這個數量一般是可以忽略的。
因此從磁盤讀取索引頁的成本可以由如下式子計算,DiskLatency 為磁盤尋址時間。
\]
那麼讀取索引頁的收益和成本的比率就是:
\]
應用分析
假設磁盤平均尋址時間為 10 毫秒,傳輸速率為 10MB 每秒,索引項大小為 20 位元組,下表給出不同索引頁大小對應的收益成本比率。
| IndexPageSize(KB) | EntriesPerPage | IndexPageUtility | IndexPageAccessCost | BenefitCostRatio |
|---|---|---|---|---|
| 2 | 68 | 6.1 | 10.2 | 0.60 |
| 4 | 135 | 7.1 | 10.4 | 0.68 |
| 8 | 270 | 8.1 | 10.8 | 0.75 |
| 16 | 541 | 9.1 | 11.6 | 0.78 |
| 32 | 1081 | 10.1 | 13.2 | 0.76 |
| 64 | 2163 | 11.1 | 16.4 | 0.68 |
| 128 | 4325 | 12.1 | 22.8 | 0.53 |
通過上表可以得出,索引頁大小在 8KB 到 32KB 是收益成本比率是最優的。索引頁過小或過大都不是好的選擇。且該索引頁大小範圍也隨着磁盤傳輸速率的提升而發生變化,當傳輸速率為 40MB 每秒,最優的索引頁大小將變成 32KB 到 128 KB。

