機器學習-感知機模型

2022 年 7 月 2 日
筆記
人工智能

一、引言

單層感知機是神經網絡的一個基本單元，類似於人類的神經網絡的一個神經元，神經網絡是由具有適應性的簡單單元(感知機)組成的廣泛並行互連的網絡，它的組織能夠模擬生物神經系統對真實世界物體所作出的交互反應。感知機可以理解為對輸入進行處理，並得到輸出結果的機器。我們似乎明白了很多，但是不明白到底為什麼明白，就和人的大腦一樣神秘。

感知機1957年由Rosenblatt提出，是神經網絡與支持向量機的基礎。是二類分類的線性分類模型，屬於判別模型，旨在求出將訓練數據進行線性劃分的分離超平面，為此，導入基於誤分類的損失函數，利用梯度下降法對損失函數進行極小化，求得感知機模型。

訓練數據集：線性可分（必存在超平面將訓練集正負實例分開）
學習目標：找到一個將訓練集正、負實例點完全正確分開的超平面
具體學習對象： $w、b$
學習策略：誤分類點到超平面S的總距離最小
算法形式：原始形式+對偶形式

二、從機器學習的角度認識感知機

1.感知機模型

輸入空間（特徵空間）是 $\chi \subseteq R^{n}$ ，輸入 $x\in \chi$ 表示實例的特徵向量
輸出空間是 $Y={+1,-1}$ ，輸出 $y \in Y$ 表示實例的類別。
輸入空間 —> 輸出空間： $f(x)=sign(w\cdot x+b) \\$

其中， $w$ 和 $b$ 為感知機模型參數，也就是我們機器學習最終要學習的參數。

sign是符號函數，

$sign(x)=\left\{\begin{matrix}+1,x>0\\ -1,x<0\end{matrix}\right.\\$

常用的經典形式，由於只有一層，又被稱為單層感知機。如下：

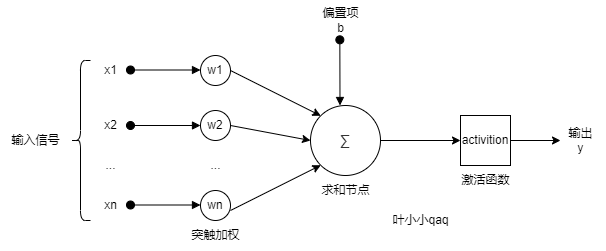
從幾何角度分析

由於：

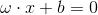
相當於n維空間的一個超平面。ω為超平面的法向量，b為超平面的截距，x為空間中的點。

當x位於超平面的正側時：

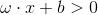
感知機被激活。

當x位於超平面的負側時：

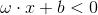
感知機被抑制。

所以，從幾何的角度來看，感知機就是n維空間的一個超平面，它把特徵空間分成兩部分。

2.分類與學習策略

確定學習策略就是定義(經驗)損失函數並將損失函數最小化。（注意這裡提到了經驗，所以學習是base在訓練數據集上的操作）

關於損失函數的選擇問題？

我們對損失函數的要求就是參數 $w，b$ 的連續可導函數，這樣才易優化（後面隨機梯度來優化，不可導何談梯度）。為此，感知機的損失函數選擇了：誤分類點到超平面 $S$ 的總距離，而不是誤分類點的總數。

數學形式：

$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b) \\$

其中 $M$ 是誤分類點的集合，給定訓練數據集 $T$ ，損失函數 $L(w,b)$ 是 $w$ 和 $b$ 的連續可導函數

3.原始算法

下面我們來看感知機的學習算法。給定一個訓練數據集T={(x1,y1),(x2,y2),…,(xN,yN)}T={(x1,y1),(x2,y2),…,(xN,yN)}
感知機的算法是誤分類驅動的，具體採用隨機梯度下降法(stochastic gradient descent). 在極小化目標函數的過程中，並不是一次使 M 中所有誤分類的點梯度下降，而是每次隨機一個誤分類的點使其梯度下降。
具體步驟為:
1.假設誤分類點的集合為 M，那麼損失函數L(w, b)的梯度為:

2.隨機選取一個誤分類的點 (xi,yi)(xi,yi)，對 w, b 更新:

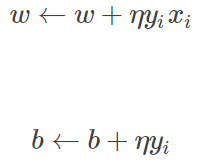
式中 η(0<η≤1)η(0<η≤1)是步長，又稱為學習率(learning_rate)，這樣，通過迭代可以使損失函數不斷減小，直到為 0.
當訓練數據集線性可分的時候，感知機學習算法是收斂的，並且存在無窮多個解，解會由於不同的初值或不同的迭代順序不同而有所不同。

4、算法——對偶形式

對偶形式的基本思想是將 $w$ 和 $b$ 表示為實例 $x_i$ 和標記 $y_i$ 的線性組合的形式，通過求解其係數而求得 $w$ 和 $b$ 。

原始形式中對誤分類點 $(x_i,y_i)$ 通過：

$w\leftarrow w+\eta y_ix_i \\ b\leftarrow b+\eta y_i$

來修正。假設對於某誤分類點 $(x_i,y_i)$ ，一共修正了 $n_i$ 次，那麼：

$w\leftarrow w+n_i\eta y_ix_i \\ b\leftarrow b+n_i\eta y_i$

那麼，對於所有數據點 $w,b$ 的變化就是：

$w\leftarrow w+\sum_{i=1}^{N} n_i\eta y_ix_i \\ b\leftarrow b+\sum_{i=1}^{N}n_i\eta y_i$

如果令初始 $w_0=0,b_0=0,\alpha_i = n_i\eta$ ，則有：

$w=\sum_{i=1}^{N} \alpha_i y_ix_i \\ b=\sum_{i=1}^{N}\alpha_i y_i$

在原始形式中，我們是要學習 $w,b$ ，現在可以轉化為 $\alpha 、b$

對偶形式：

輸入： $T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}\\ x_i\in {X}=\bf{R}^n , y_i\in {Y} ={-1,+1}, i=1,2,\dots, N; 0< \eta \leqslant 1$
輸出： $\alpha ,b; f(x)=sign(\sum_{j=1}^N\alpha_jy_jx_j\cdot x+b)\\alpha=(\alpha_1,\alpha_2,...\alpha_N)^T$
步驟：

$\alpha \leftarrow 0,b\leftarrow 0$
訓練集中選取數據 $(x_i,y_i)$
如果 $y_i\left(\sum_{j=1}^N\alpha_jy_jx_j\cdot x+b\right) \leqslant 0$ $\alpha_i\leftarrow \alpha_i+\eta \\b\leftarrow b+\eta y_i$
轉至(2)，直至訓練集中沒有誤分類點
步驟解釋：
步驟1：和前面一樣，初始值取0
步驟2：每次也是選取一個數據
步驟3:

如果數據點是誤判點的話，開始修正
這裡關注一下梯度的計算：對於每一個數據 $(x_i,y_i)$ 每一次修正來說， $\alpha_i$ 的變化量是： $\eta$ ， $b$ 還是 $\eta y_i$ 不變

步驟4：與原始形式一樣，感知機學習算法的對偶形式迭代是收斂的，存在多個解

Gram matrix

對偶形式中，訓練實例僅以內積的形式出現。

為了方便可預先將訓練集中的實例間的內積計算出來並以矩陣的形式存儲，這個矩陣就是所謂的Gram矩陣

$G=[x_i\cdot x_j]_{N\times N} \\$

三、代碼實現

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

#加載數據
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target

df.columns = [
    'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
print(df.label.value_counts())

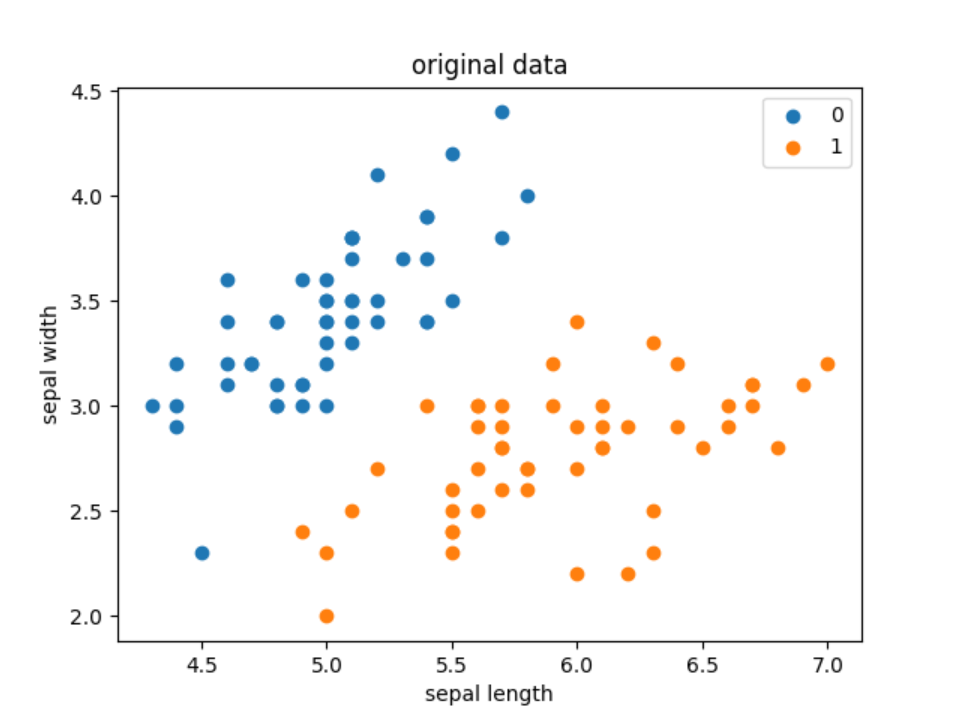
#畫出原始數據離散圖
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.title('original data')
plt.legend()
plt.show()

data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
print("X: ",X)
print("y: ",y)
y = np.array([1 if i == 1 else -1 for i in y])

#感知機模型
# 數據線性可分，二分類數據
# 此處為一元一次線性方程
class Model:
    def __init__(self):
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data

    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y

    # 隨機梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y, X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

    def score(self):
        pass

perceptron = Model()
perceptron.fit(X, y)

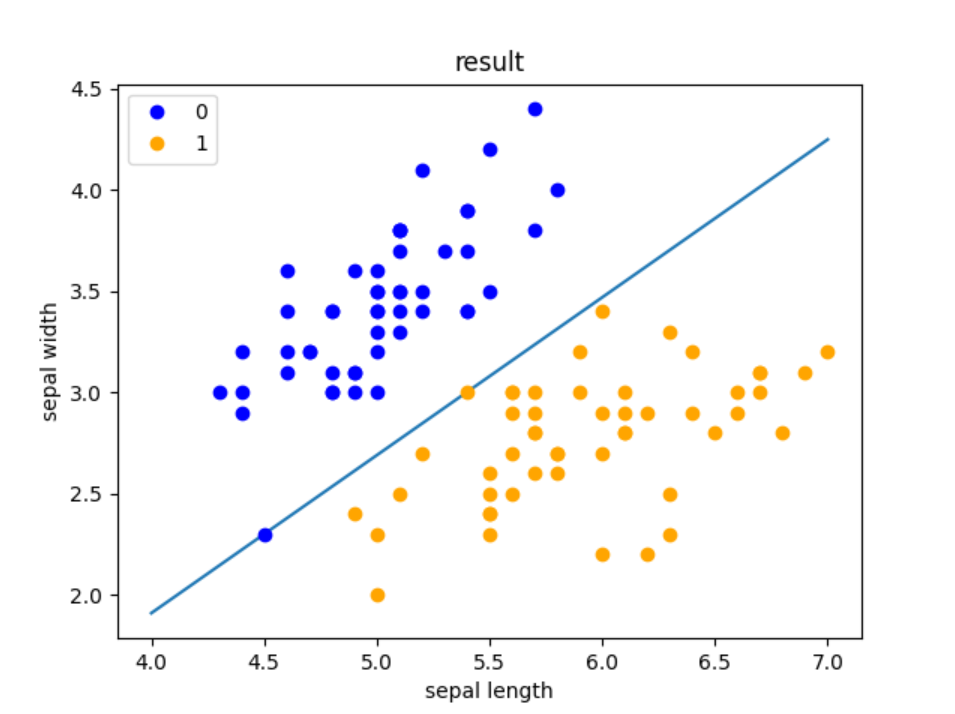
#畫出訓練結果
x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.title('result')
plt.legend()
plt.show()

輸出結果：

以上部分內容來自於網絡，如有侵權，聯繫刪除

Tags: 人工智能

機器學習-感知機模型

一、引言