梯度下降算法實現原理(Gradient Descent)
- 2022 年 6 月 29 日
- 筆記
概述
梯度下降法(Gradient Descent)是一個算法,但不是像多元線性回歸那樣是一個具體做回歸任務的算法,而是一個非常通用的優化算法來幫助一些機器學習算法求解出最優解的,所謂的通用就是很多機器學習算法都是用它,甚至深度學習也是用它來求解最優解。所有優化算法的目的都是期望以最快的速度把模型參數θ求解出來,梯度下降法就是一種經典常用的優化算法。
梯度下降法的思想

思想就類比於生活中的一些事情,比如你去詢問你的一個朋友工資多少,他不會告訴你,但是他會讓你去猜,然後告訴你猜的結果。你每說出一次答案,他就會說猜高了或是猜低了,這樣下去你就會奔着對方的回答繼續猜下去,總有一次能猜到正確答案。梯度下降法就是這樣,你得去試很多次,而且我們在試的過程中還得想辦法知道是不是在猜對的路上,說白了就是得到正確的反饋再調整。
一般你玩兒這樣的遊戲的時候,一開始第一下都是隨機瞎猜一個對吧,那對於計算機來說是不是就是隨機取值,也就是說你有θ =W1…Wn,這裡θ強調一下不是一個值,而是一個向量就是一組 W,一開始的時候我們通過隨機把每個值都給它隨機出來。有了θ我們可以去根據算法就是公式去計算出來^y ,比如 y^ = Xθ ,然後根據計算^y 和真實y之間的損失,比如 MSE,然後調整θ再去計算MSE。
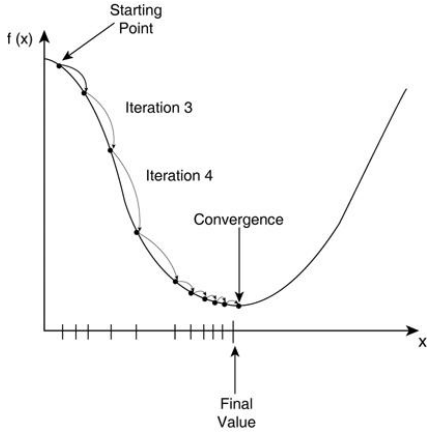
這個調整正如咱們前面說的肯定不是瞎調整,當然這個調整的方式很多,你可以整體θ每個值調大一點,也可以整體θ每個值調小一點,也可以一部分調大一部分調小。第一次θ 0我們可以得到第一次的 MSE 就是 Loss0,調整後第二次θ1對應可以得到第二次的 MSE 就是 Loss1,如果 loss 變小是不是調對了,就應該繼續調,如果loss反而變大是不是調反了,就應該反過來調。直到 MSE 我們找到最小值時計算出來的θ^ 就是我們的最優解。這個就好比下山過程,我們把 loss 看出是曲線就是山谷,如果走過來就再往回調,所以是一個迭代的過程。
梯度下降法公式
這裡梯度下降法的公式就是一個式子指導計算機迭代過程中如何去調整θ,不需要推導和證明,就是總結出來的。
公式: Wjt+1 = Wjt – η × gradientj
這裡的 Wj就是θ中的某一個 j=0…n,這裡的η就是圖裡的 learningstep,很多時候也叫學習率 learning rate,很多時候也用α表示,這個學習率我們可以看作是下山邁的步子的大小,步子邁的大下山就快。

學習率一般都是正數,那麼在山左側梯度是負的,那麼這個負號就會把 W 往大了調,如果在山右側梯度就是正的,那麼負號就會把 W 往小了調。每次 Wj 調整的幅度就是η*gradient,就是橫軸上移動的距離。
如果特徵或維度越多,那麼這個公式用的次數就越多,也就是每次迭代要應用的這個式子 n+1 次,所以其實上面的圖不是特別准,因為θ對應的是很多維度,應每一個維度都可以畫一個這樣的圖,或者是一個多維空間的圖。
W0t+1 =W0t – h×g0
W1t+1 =W1t – h × g1
Wjt+1 =Wjt – h × gj
Wnt+1 =Wnt – h × gn

所以觀察圖我們可以發現不是某一個θ0 或θ1找到最小值就是最優解,而是它們一起找到 J 最小的時候才是最優解。
學習率設置的學問
公式: Wjt+1 = Wjt – η × gradientj
根據我們上面講的梯度下降法公式,我們知道η是學習率,設置大的學習率 Wj 每次調整的幅度就大,設置小的學習率 Wj 每次調整的幅度就小,然而如果步子邁的太大也會有問題其實,可能一下子邁到山另一頭去了,然後一步又邁回來了,使得來來回回震蕩。步子太小呢就一步步往前挪,也會使得整體迭代次數增加。

學習率的設置是門學問,一般我們會把它設置成一個比較小的正整數,0.1、0.01、0.001、0.0001,都是常見的設定數值,一般情況下學習率在整體迭代過程中是一直不變的數,但是也可以設置成隨着迭代次數增多學習率逐漸變小,因為越靠近山谷我們就可以步子邁小點,省得走過,還有一些深度學習的優化算法會自己控制調整學習率這個值。

全局最優解

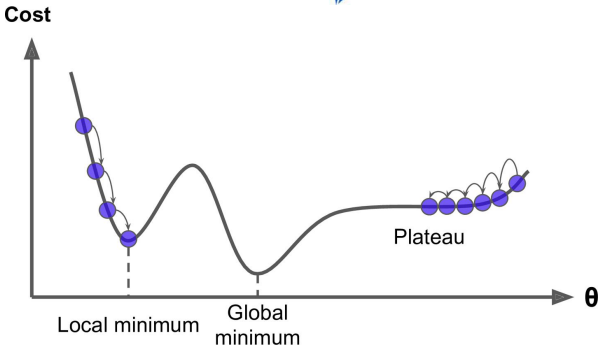
上圖可以看出如果損失函數是非凸函數,梯度下降法是有可能落到局部最小值的,所以其實步長不能設置的太小太穩健,那樣就很容易落入局部最優解,雖說局部最小也沒大問題,因為模型只要是堪用的就好嘛,但是我們肯定還是盡量要奔着全局最優解去。
梯度下降法流程:
- 隨機θ,隨機一組數值W0…Wn
- 求梯度,為什麼是梯度?因為梯度代表曲線某點上的切線的斜率,沿着切線往下下降就相當於沿着坡度最陡峭的方向下降
- if g<0, θ 變大,if g>0, θ 變小
- 判斷是否收斂 convergence,如果收斂跳出迭代,如果沒有達到收斂,回第 2 步繼續
Question?
1.. 如何隨機?
2..怎麼求梯度?
3..如何調整θ或W?
4..怎麼判斷收斂?
Answer
1..np.random.rand()或者 np.random.randn()
2..gradientj = \(\frac{∂Loss}{W_j}\)
3..Wit+1 = Wit – h × gradienti
4..判斷收斂這裡使用 g=0 其實並不合理,因為當損失函數是非凸函數的話 g=0 有可能是極大值對嗎!所以其實我們判斷 loss 的下降收益更合理,當隨着迭代 loss 減小的幅度即收益不再變化就可以認為停止在最低點,收斂!
總結,講解完梯度下降法流程同學們會發現這裡仍然第 2 步不是很清楚怎麼去做,但是其它步驟其實都已經清楚比如用編程如何去做對吧,下面就來講第 2 步該怎麼去進一步推導出來表達式。
損失函數的導函數
求解上面梯度下降的第 2 步,即我們要推導出損失函數的導函數來。
θ = θ – α · \(\frac{∂J(θ)}{∂θ}\)
下面公式推導 J(θ)是損失函數,q j 是某個特徵維度 Xj 對應的權值係數,也可以寫成 Wj。這裡我們還是在接着之前的多元線性回歸往下講,所以損失函數是 MSE,所以下面公式表達的是因為我們的 MSE 中 X、y 是已知的,θ是未知的,而θ不是一個變量而是一堆變量,所以我們只能對含有一推變量的函數 MSE 中的一個變量求導,即偏導,下面就是對θj 求偏導。
\]
\]
\]
\]
\(x^2\) 的導數就是 2x,根據鏈式求導法則,我們可以推出第一步。然後是多元線性回歸,所以 hθ(x) 就是 wTx 也是w0·x0+w1·x1+…+wn·xn亦是\(\sum_{n=0}^n{w_ix_i}\),到這裡我們是對θj 來求偏導,那麼和 Wj 沒有關係的可以忽略不計,所以只剩下 Xj。
我們可以得到結論就是θj 對應的 gradient 與預測值^y 和真實值 y 有關,這裡^y 和 y 是列向量,同時還與θj 對應的特徵維度 Xj 有關,這裡 Xj 是原始數據集矩陣的第 j 列。如果我們分別去對每個維度 W0…Wn 求偏導,即可得到所有維度對應的梯度值。
g0 = (hθ(x) – y)·X0
g1 = (hθ(x) – y)·X1
gj = (hθ(x) – y)·Xj
gn = (hθ(x) – y)·Xn
總結:
θjt+1 = θjt – η · gj = θjt – η · (hθ(x) – y) · xj
三種梯度下降法
三種梯度下降區別和優缺點
區別:其實三種梯度下降的區別僅在於第 2 步求梯度所用到的 X 數據集的樣本數量不同!它們每次學習(更新模型參數)使用的樣本個數,每次更新使用不同的樣本會導致每次學習的準確性和學習時間不同。

全量梯度下降
Batch Gradient Descent
θjt+1 = θjt – η · \(\sum_{i=1}^m{(h_θ(x^i) – y^i)} · x^i_j\)
在梯度下降中,對於θ的更新,所有的樣本都有貢獻,也就是參與調整θ。其計算得到的是一個標準梯度。因而理論上來說一次更新的幅度是比較大的。如果樣本不多的情況下,當然是這樣收斂的速度會更快啦。全量梯度下降每次學習都使用整個訓練集,因此其優點在於每次更新都會朝着正確的方向進行,最後能夠保證收斂於極值點(凸函數收斂於全局極值點,非凸函數可能會收斂於局部極值點),但是其缺點在於每次學習時間過長,並且如果訓練集很大以至於需要消耗大量的內存,並且全量梯度下降不能進行在線模型參數更新。

隨機梯度下降
Stochastic Gradient Descent
θjt+1 = θjt – η · (hθ(x(i)) – y(i)) · xj(i)
梯度下降算法每次從訓練集中隨機選擇一個樣本來進行學習。批量梯度下降算法每次都會使用全部訓練樣本,因此這些計算是冗餘的,因為每次都使用完全相同的樣本集。而隨機梯度下降算法每次只隨機選擇一個樣本來更新模型參數,因此每次的學習是非常快速的,並且可以進行在線更新。隨機梯度下降最大的缺點在於每次更新可能並不會按照正確的方向進行,因此可以帶來優化波動(擾動)。
不過從另一個方面來看,隨機梯度下降所帶來的波動有個好處就是,對於類似盆地區域(即很多局部極小值點)那麼這個波動的特點可能會使得優化的方向從當前的局部極小值點跳到另一個更好的局部極小值點,這樣便可能對於非凸函數,最終收斂於一個較好的局部極值點,甚至全局極值點。由於波動,因此會使得迭代次數(學習次數)增多,即收斂速度變慢。不過最終其會和全量梯度下降算法一樣,具有相同的收斂性,即凸函數收斂於全局極值點,非凸損失函數收斂於局部極值點。

小批量梯度下降
Mini-Batch Gradient Descent
θjt+1 = θjt – η · \(\sum_{i=1}^b{(h_θ(x^i) – y^i)} · x^i_j\)
註:b = batch_size
Mini-batch 梯度下降綜合了 batch 梯度下降與 stochastic 梯度下降,在每次更新速度與更新次數中間取得一個平衡,其每次更新從訓練集中隨機選擇 batch_size,batch_size< m 個樣本進行學習。相對於隨機梯度下降算法,小批量梯度下降算法降低了收斂波動性,即降低了參數更新的方差,使得更新更加穩定。相對於全量梯度下降,其提高了每次學習的速度。並且其不用擔心內存瓶頸從而可以利用矩陣運算進行高效計算。一般而言每次更新隨機選擇[50,256]個樣本進行學習,但是也要根據具體問題而選擇,實踐中可以進行多次試驗,選擇一個更新速度與更次次數都較適合的樣本數。

梯度下降法的問題與挑戰
雖然梯度下降算法效果很好,並且廣泛使用,但是不管用上面三種哪一種,都存在一些挑戰與問題需要解決:
- 選擇一個合理的學習速率很難。如果學習速率過小,則會導致收斂速度很慢。如果學習速率過大,那麼其會阻礙收斂,即在極值點附近會振蕩。
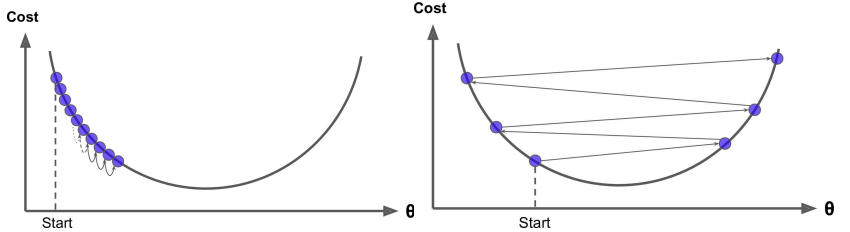
- 學習速率調整(又稱學習速率調度,Learning rate schedules 試圖在每次更新過程中,改變學習速率,如退火。一般使用某種事先設定的策略或者在每次迭代中衰減一個較小的閾值。無論哪種調整方法,都需要事先進行固定設置,這邊便無法自適應每次學習的數據集特點。
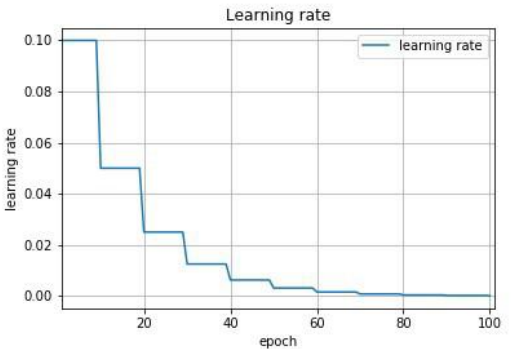
- 模型所有的參數每次更新都是使用相同的學習速率。如果數據特徵是稀疏的或者每個特徵有着不同的取值統計特徵與空間,那麼便不能在每次更新中每個參數使用相同的學習速率,那些很少出現的特徵應該使用一個相對較大的學習速率。

- 對於非凸目標函數,容易陷入那些次優的局部極值點中,如在神經網路中。那麼如何避免呢。Dauphin 指出更嚴重的問題不是局部極值點,而是鞍點(These saddle points are usually surrounded by a plateau of the same error, which makes it notoriously hard for SGD to escape, as the gradient is close to zero in all dimensions.)
輪次和批次
輪次:epoch,輪次顧名思義是把我們已有的訓練集數據學習多少輪
批次:batch,批次這裡指的的我們已有的訓練集數據比較多的時候,一輪要學習太多數據,那就把一輪次要學習的數據分成多個批次,一批一批數據的學習。
舉個例子,這就好比有一本唐詩 300 首需要大家背誦,如果要給你一周時間要你背誦完,或許你很聰明可以背完,但是估計也不敢說一下子全都記得特別牢,甚至到可以出口成章的地步吧。那通常人是怎麼做的呢?是不是就是接下來多花幾周,重複之前一周的動作,把 300 首唐詩多背幾次,比如花 10 周把 300 首唐詩全部倒背如流了,然後又花了 10 周時間把 300 首唐詩又背誦到了滾瓜爛熟的地步終於可以出口成唐詩了。那麼剛提到的 10 周、又 10 周放在 AI 領域那麼就是所謂的訓練了10個輪次又 10 個輪次,總共 20 個輪次。
再回顧上面一段話,我們假設你很聰明,也就是 AI 訓練的電腦性能處理能力非常好,如果是普通人或者一般的電腦,很有可能一周都不可能背誦完 300 首,也就是內存一下子裝不下那麼大的數據量,或者處理器計算能力沒有那麼快。當數據量大的情況下,這是很常見的現在,那麼為了可以順利背下來 300 首唐詩到舉一反三出口成章的地方,也就是為了訓練出來 model 模型,我們只能把一個輪次需要的數據分成多個批次來一點點計算,放到背唐詩的例子中,說白了就是一周背不下來 300 首唐詩,那麼我們就一周背 50 首唐詩吧比如說,這樣我們就需要 6 個批次把一輪數據背完,一個批次所需要的數據batch_size 就是50。
還有就是對於三種梯度下降來說,全量梯度下降就是每一輪次用到全量的數據,然後一次迭代就是一個輪次,然後用全量數據計算梯度來更新一下 W。隨機梯度下降每一個輪次也需要計算所有數據,但是有多少數據就會分為多少個批次,即是一個批次一次迭代,就只用一條數據計算梯度來更新一下 W,所以隨機梯度下降一個輪次中的更新 W 的次數等於樣本總數。最後就是 mini-batch 梯度下降,每一個輪次也需要計算所有數據,但是輪次分成多 少 個 批 次 取 決 於 batch_size , batch_size 大 需 要 的 輪 次 就 少 , 比 如batch_size=num_samples,那就等價於全量批量梯度下降,batch_size=1 那就等價於隨機梯度下降。
代碼實戰梯度下降法與優化
全量梯度下降
創建數據集 X、y
點擊查看代碼
np.random.seed(1)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X
創建超參數
點擊查看代碼
learning_rate = 0.001
n_iterations = 1000
1. 初始化 θ,w0…wn,正太分佈創建
點擊查看代碼
theta = np.random.randn(2, 1)
點擊查看代碼
# 4,不會設置閾值,直接設置超參數,迭代次數,迭代次數到了,我們就認為收斂了
for _ in range(n_iterations):
# 2,接着求梯度 gradient
gradients = X_b.T.dot(X_b.dot(theta)-y)
# 3,應用公式調整 theta 值,theta_t + 1 = theta_t - grad * learning_rate
theta = theta - learning_rate *
上面代碼值得一提的是,X_b.T是X的轉置,也就是n行m列的矩陣,然後(X_b.dot(theta)-y)是一個 m 行 1 列的列向量,這樣矩陣乘以向量會得到一個 n 行一列的列向量,相當於一下子計算出來所有維度對應的梯度值。然後第 3 步直接去應用所有的梯度到所有的 theta 上面。
#### 隨機梯度下降
創建數據集 X、y
點擊查看代碼
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
設置超參數,n_epochs 是迭代的輪次,m 是樣本總數,也就是每個輪次迭代的批次
點擊查看代碼
n_epochs = 10000
m = 100
learning_rate = 0.001
1,初始化 theta,w0…wn,正太分佈創建
點擊查看代碼
theta = np.random.randn(2, 1)
這裡是雙層 for 循環,第一層 for 循環是分輪次來計算,第二層 for 循環是分批次來計算random_index = np.random.randint(m)是隨機的從數據集中取一條數據的索引,然後根據索引來切片操作取隨機出來數據的 Xi 和 yi,每次 W 更新所需要的梯度的求解只用到一條樣本的信息。
點擊查看代碼
for epoch in range(n_epochs):
for i in range(m):
# 2, 求 gradient Xi.T * (Xi * theta - yi)
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = xi.T.dot(xi.dot(theta)-yi)
# 3, 調整 theta
theta = theta - learning_rate *
小批量梯度下降
創建數據集 X、y
點擊查看代碼
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
設置超參數,n_epochs 是迭代的輪次,m 是樣本總數,batch_size 是每個批次迭代需要的數據量,然後 num_batches 是一輪需要多少個迭代需要相除再向上取整
點擊查看代碼
learning_rate = 0.001
n_epochs = 10000
m = 100
batch_size = 10
num_batches = int(m/batch_size)
1,初始化 theta,w0…wn,正太分佈創建
點擊查看代碼
theta = np.random.randn(2, 1)
和之前代碼差別無非就是切片取出來的是 batch_size 個樣本數據,然後求解梯度而已
點擊查看代碼
for epoch in range(n_epochs):
for i in range(num_batches):
# 2, 求 gradient Xi.T * (Xi * theta - yi)
random_index = np.random.randint(m)
x_batch = X_b[random_index:random_index+batch_size]
y_batch = y[random_index:random_index+batch_size]
gradients = x_batch.T.dot(x_batch.dot(theta)-y_batch)
# 3, 調整 theta
theta = theta - learning_rate * gradient







