RepVGG：VGG，永遠的神！ | CVPR 2021

RepVGG將訓練推理網絡結構進行獨立設計，在訓練時使用高精度的多分支網絡學習權值，在推理時使用低延遲的單分支網絡，然後通過結構重參數化將多分支網絡的權值轉移到單分支網絡。RepVGG性能達到了SOTA，思路簡單新穎，相信可以在上面做更多的工作來獲得更好的性能。

來源：曉飛的算法工程筆記公眾號

論文: RepVGG: Making VGG-style ConvNets Great Again

論文地址：//arxiv.org/abs/2101.03697
論文代碼：//github.com/megvii-model/RepVGG

Introduction

目前，卷積網絡的研究主要集中在結構的設計。複雜的結構儘管能帶來更高的準確率，但也會帶來推理速度的減慢。影響推理速度的因素有很多，計算量FLOPs往往不能準確地代表模型的實際速度，計算量較低的模型不一定計算更快。因此，VGG和ResNet依然在很多應用中得到重用。
基於上述背景，論文提出了VGG風格的單分支網絡結構RepVGG，能夠比結構複雜的多分支網絡更優秀，主要包含以下特點：

模型跟VGG類似，不包含任何分支，無需保存過多的中間結果，內存佔用少。
模型僅包含$3\times 3$卷積和ReLU，計算速度快。
具體的網絡結構(包括深度和寬度)不需要依靠自動搜索、人工調整以及複合縮放等複雜手段進行設計，十分靈活。

當然，想要直接訓練簡單的單分支網絡來達到與多分支網絡一樣的精度是很難的。由於多分支網絡中的各個分支在訓練時的權重變化不定，所以多分支網絡可看作是大量簡單網絡的合集，而且其能夠避免訓練時的梯度彌散問題。雖然如此，但多分支網絡會損害速度，所以論文打算訓練時採用多分支網絡，而推理時仍然使用單分支網絡，通過新穎的結構性重參數化(structural re-parameterization)將多分支網絡的權值轉移到簡單網絡中。

Building RepVGG via Structural Re-param

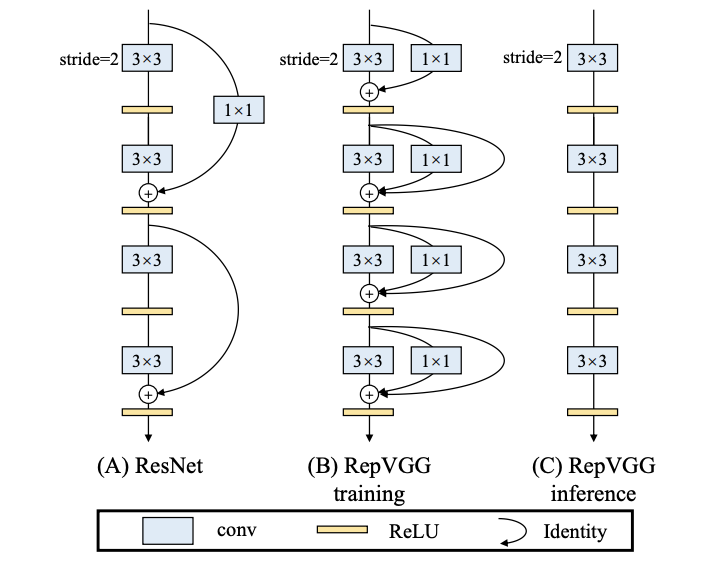
Training-time Multi-branch Architecture

由於多分支的存在，使得多分支網絡相當於一個包含大量小網絡的集合，但其推理速度會有較大影響，所以論文僅在訓練時使用多分支進行訓練，訓練完成後將其權值轉移到簡單網絡中。為了夠包含大量更簡單的模型，論文在$3\times 3卷積的基礎上添加ResNet-like的identity分支和$1\times 1分支構成building block，然後堆疊成訓練模型。假設多分支網絡包含n個building block，則其可以表達$3^n$種簡單網絡結構。

Re-param for Plain Inference-time Model

在開始描述最重要的權值轉換之前，先進行以下定義：

定義$3\times 3卷積為W^{(3)}\in \mathbb{R}^{C_2\times C_1\times 3\times 3}，$1\times 1卷積為W^{(1)}\in \mathbb{R}^{C_2\times C_1}。
定義\mu^{(3)}、\sigma^{(3)}、\gamma^{(3)}和\beta^{(3)}為跟在$3\times 3卷積後面的BN層的累計均值、標準差、學習到的縮放因子和偏置，跟在$1\times 1卷積後面的BN層的參數為\mu^{(1)}、\sigma^{(1)}、\gamma^{(1)}和\beta^{(1)}，跟在identity分支後面的BN層參數為\mu^{(0)}、\sigma^{(0)}、\gamma^{(0)}和\beta^{(0)}。
定義輸入為M^{(1)}\in \mathbb{R}^{N\times C_1\times H_1\times W_1}，輸出為M^{(2)}\in \mathbb{R}^{N\times C_c\times H_2\times W_2}。
定義*為卷積操作。

假設C_1=C_2、H_1=H_2以及W_1=W_2，則有：

若輸入輸出維度不相同，則去掉identity分支，即只包含前面兩項。bn代表是推理時的BN函數，一般而言，對於\forall 1\leq i \leq C_2，有：

權值轉換的核心是將BN和其前面的卷積層轉換成單個包含偏置向量的卷積層。假設\{W^{‘}, b^{‘}\}為從\{W, \mu, \sigma, \gamma, \beta\}轉換得到的核權值和偏置，則有：

轉換後的卷積操作與原本的卷積+BN操作是等價的，即：

上述的轉換也可應用於identity分支，將identity mapping視作卷積核為單位矩陣的$1\times 1$卷積。

以上圖為例，在C_2=C_1=2的情況下，將3個分支分別轉換後得到1個$3\times 3卷積和兩個$1\times 1卷積，最終的卷積偏置由3個卷積的偏置直接相加，而最終的卷積核則是將兩個$1\times 1卷積核加到$3\times 3卷積核中心。需要注意的是，為了達到轉換的目的，訓練時的$3\times 3卷積分支和$1\times 1卷積分支需要有相同的步長，而$1\times 1卷積的填充要比$3\times 3卷積的小一個像素。

Architectural Specification

RepVGG是VGG風格的網絡，主要依賴$3\times 3卷積，但沒有使用最大池化，而是使用步長為2的$3\times 3卷積作為替換。RepVGG共包含5個階段，每個階段的首個卷積的步長為2。對於分類任務，使用最大池化和全連接層作為head，而其它任務則使用對應的head。

每個階段的層數的設計如上表所示，除首尾兩個階段使用單層外，每個階段的層數逐漸增加。而每個階段的寬度則通過縮放因子a和b進行調整，通常b \gt a，保證最後一個階段能夠提取更豐富的特徵。為了避免第一階段採用過大的卷積，進行了min(64, 64a)的設置。
為了進一步壓縮參數，論文直接在特定的層加入分組卷積，從而達到速度和準確率之間的trade-off，比如RepVGG-A的3rd, 5th, 7th, …, 21st層以及RepVGG-B的23rd, 25th和27th層。需要注意，這裡沒有對連續的層使用分組卷積，主要為了保證通道間的信息交流。