機器學習回顧篇(6):KNN算法
- 2019 年 10 月 4 日
- 筆記
1 引言
本文將從算法原理出發,展開介紹KNN算法,並結合機器學習中常用的Iris數據集通過代碼實例演示KNN算法用法和實現。
2 算法原理
KNN(kNN,k-NearestNeighbor)算法,或者說K近鄰算法,應該算是機器學習中眾多分類算法最好理解的一個了。古語有云:物以類聚,人以群分。沒錯,KNN算法正是這一思想為核心,對數據進行分類。
而所謂K近鄰,意思是對於每一個待分類樣本,都可以以與其最近的K個樣本點的多數分類來來進行劃分。舉個例子,辦公室新來了一個同事,他的位置邊上坐着的10個(K=10)同事都是大多是Python程序員,我們會猜測這個新同事是Python程序員;如果把判斷依據擴大的整個辦公室,假設辦公室有50個人(K=50),其中java程序員35個,那麼我們就會認為這個新同事是java程序員。
回到KNN算法,對數據進行分類的思想和流程與我們判斷新同事的工作是一樣的:
(1)計算待分類樣本與所有已知分類的樣本之間的距離;
(2)對多有距離進行按升序排序;
(3)取前K個樣本;
(4)統計前K個樣本中各分類出現的頻數;
(5)將待分類樣本劃分到頻數最高的分類中。
好了,我想現在你應該對KNN算法有了基本的認識了。不過有幾個問題還得明確一下:
K值如何確定?
如何度量距離?
先來說說如何確定K值。對於K值,從KNN算法的名稱中,我們可以看出K值得重要性是毋庸置疑的。我們用下圖的例子來說一說K值得樣本分類的重要性:
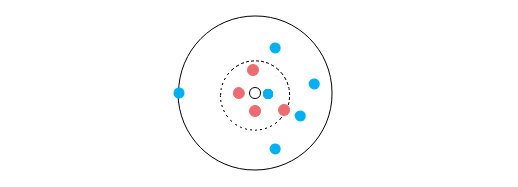
圖中所有圓點構成一個數據集,圓點顏色代表分類,那麼,圖中無色圓點劃分到哪個類呢?
當K=1時,離透明點最近的點是藍點,那麼我們應該將透明圓點劃分到藍點所在類別中;
當K=5時,離透明點最近的5個點中有4個紅點,1個藍點,那麼我們應該將透明圓點劃分到紅點所屬的類別中;
當K=10時,離透明點最近的10個點中有4個紅點,6個藍點,那麼我們應該將透明圓點劃分到藍點所屬的類別中。
你看,最終的結果因K值而異,K值過大過小都會對數據的分類產生不同程度的影響:
當K取較小值時,意味着根據與待測樣本距離較小的小範圍內樣本對待測樣本的類別進行預測,這麼做的優點是較遠範圍的樣本數據不會對分類結果產生影響,訓練誤差(機器學習模型在訓練數據集上表現出的誤差叫做訓練誤差)較小。但卻容易導致過擬合現象的產生,增大泛化誤差(在任意一個測試數據樣本上表現出的誤差的期望值叫做泛化誤差)模型變得複雜,一旦帶測驗本附近有異常數據存在,分類經過就可能會產生較大的影響,例如上圖上K=1時,如果最近的藍點是異常數據,那麼對透明圓點的預測結果就因此變得異常。
當K較大值時,意味着綜合更大範圍的樣本對待測驗本類別進行預測,優點是可以減少泛化誤差,但訓練誤差隨之增大,模型變得簡單。一個極端的例子就是如上圖所示,當K取值為整個數據集規模時,整個預測過程就沒有太大價值,所有待測樣本類別都會被預測為數據集中樣本數量多的一類。
對於K值的確定,目前並沒有專門的理論方案,一個較普遍的做法就是將數據集分為兩部分,一部分用作訓練集,一部分用作測試集,從K取一個較小值開始,逐步增加K值,最終去準確率最高的一個K值。
一般而言,K取值不超過20,上限是n的開方,隨着數據集的增大,K的值也要增大。另外,K的取值盡量要取奇數,以保證在計算結果最後會產生一個較多的類別,如果取偶數可能會產生相等的情況,不利於預測。
關於距離度量,我們最熟悉的、使用最廣泛的就是歐式距離了。對於$d$維數據點$x$和$y$之間的歐氏距離定義為:
除了歐氏距離外,距離度量方法還有餘弦距離、哈曼頓距離、切比雪夫距離等,但使用不多,不介紹了。
最後總結一下KNN算法:
KNN的主要優點有:
1) 理論成熟,思想簡單,既可以用來做分類也可以用來做回歸
2) 可用於非線性分類
3) 和樸素貝葉斯之類的算法比,對數據沒有假設,準確度高,對異常點不敏感
4) 由於KNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對於類域的交叉或重疊較多的待分樣本集來說,KNN方法較其他方法更為適合
5)該算法比較適用於樣本容量比較大的類域的自動分類,而那些樣本容量較小的類域採用這種算法比較容易產生誤分
KNN的主要缺點有:
1)計算量大,尤其是特徵數非常多的時候
2)樣本不平衡的時候,對稀有類別的預測準確率低
3)使用懶散學習方法,基本上不學習,導致預測時速度比起邏輯回歸之類的算法慢
4)相比決策樹模型,KNN模型可解釋性不強
3 Python實現KNN算法¶
我們用Python來手動實現KNN算法,採用的數據集為Iris數據集,可以從UCI官網上下載,然後放到當前目錄下:
# -*- coding: utf-8 -*- import pandas as pd from sklearn.utils import shuffle
# 讀取數據,並指定列名 names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class_name'] # 為每列指定一個列名 iris_data = pd.read_csv('iris.data',names=names)
查看一下數據的基本情況:
iris_data.describe().T
可以看到,各屬性均值、值域各不相同,為了消除各屬性因為取值範圍的不同對算法的不良影響,最好對數據進行歸一化:
# 數據歸一化 for col in names[:-1]: clo_max = iris_data[col].max() clo_min = iris_data[col].min() iris_data[col] = (iris_data[col] - clo_min) / (clo_max - clo_min)
iris_data.head(10)
源數據集是根據樣本類別進行排序的,所以需要先打亂數據:
iris_data = shuffle(iris_data) # 打亂數據 iris_data = iris_data.reset_index(drop=True) # 重設索引 iris_data.head(10)
將數據集分為兩部分,一部分用作訓練模型,一部分用作測試模型:
train_data = iris_data[:120] # 前120條作為訓練集 test_data = iris_data[120:] # 120~150作為作測試集
def distance(data1,data2): # 計算兩點距離 dist = 0 for i, j in zip(data1, data2): dist = dist + (i - j) ** 2 dist = dist ** 0.5 return dist
def knn(predict_data, train_data, k): dist_list = [] for index, row in train_data.iterrows(): # 與每一個訓練集中數據計算距離 dist = distance(predict_data[:-1], row[:-1]) dist_list.append(dist) dist_df = train_data.loc[:,['class_name']] dist_df['distance'] = dist_list # 將距離和類標籤放入同一DataFrame中 dist_df = dist_df.sort_values(by=['distance'],ascending=True) # 根據距離進行升序排序 dist_df_k = dist_df[:k] #取前K個 predict_class = 'Iris-setosa' class_num = 0 for class_name in ['Iris-setosa','Iris-versicolor','Iris-virginica']: # 統計三個類別那個最多 temp_num = dist_df_k.groupby(['class_name']).size().get(class_name,0) # 各類別的數量 if temp_num > class_num: predict_class = class_name class_num = temp_num return predict_class
def predict(test_data, train_data, k): predict_class_list = [] for _, test_row in test_data.iterrows(): predict_class = knn(test_row, train_data, k) predict_class_list.append(predict_class) result_df = test_data.copy() result_df['predict_class'] = predict_class_list print(result_df.loc[:,['class_name','predict_class']].head(10)) return result_df result_df = predict(test_data, train_data, 10)
# 計算準確率 def calculate_accuracy(result_df): sum = len(result_df) right = 0 for index, row in result_df.iterrows(): if row['class_name'] == row['predict_class']: right += 1 accuracy = right / sum print('準確率:',accuracy) calculate_accuracy(result_df)
4 sklearn庫中的KNN算法¶
最後通過調用sklearn庫中的KNN算法來實現Iris數據預測。
雖然sklearn苦衷自帶Iris數據集,不過為了更好與上一章節實現進行對比,我們還是和上面一樣從文件中讀取數據。
from sklearn.neighbors import KNeighborsClassifier # KNN算法 from sklearn.model_selection import train_test_split # 分割數據集 from sklearn.preprocessing import MinMaxScaler # 數據歸一化 import pandas as pd
# 讀取數據,並指定列名 names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class_name'] # 為每列指定一個列名 iris_data = pd.read_csv('iris.data',names=names)
在使用sklearn庫進行預測時,屬性和分類必須分開保存:
iris_x = iris_data.loc[:,['sepal_length', 'sepal_width', 'petal_length', 'petal_width']] # 取出所有屬性 iris_y = iris_data.loc[:,['class_name']] # 取出所有分類
用sklearn自帶庫對數據進行歸一化:
iris_x = MinMaxScaler().fit_transform(iris_x)
# 將數據分為訓練集和測試機,train_test_split自帶打亂功能 train_data_x,test_data_x,train_data_y,test_data_y = train_test_split(iris_x, iris_y, test_size=0.25, random_state=0)
train_data_y = [elem[0] for elem in train_data_y.values] # 轉換為一維list,訓練模型時類別最好使用一維數組存放
# 定義模型 knn=KNeighborsClassifier(n_neighbors=10)
# 訓練模型 knn.fit(train_data_x,train_data_y)
result=knn.predict(test_data_x) # 預測
test_data_y = test_data_y.reset_index(drop=True) # 重設索引,不然索引也是亂序的,下面不好遍歷
# 計算準確率 count=0 for i,row in test_data_y.iterrows(): if result[i]==row['class_name']: count+=1 print('準確率:',float(count)/float(len(test_data_y)))
