理解HMM算法
長這樣:

理解的前提:

(1)狀態:生成觀測值的變量(上圖中的「吃」和「睡」)。
(2)觀測值:狀態乘上輸出概率對應的輸出(上圖中的橙色節點)。
(3)輸出概率:輸出概率矩陣裏面的某個元素(狀態和觀測值兩層之間的某個權重參數)。
(4)輸出概率矩陣:由輸出概率組成的矩陣。
(5)bi: 第i個狀態(比如」睡「)輸出所有觀測值對應的概率構成的行向量(上圖中所有紅線構成的行向量)。
(6)o1:表示我要輸出第一個觀測值。不是把o1做為自變量輸入到bi中,只是一個記號(個人表示沒什麼用)。
(7)Πi:走 第i個狀態的初始概率(p(start->吃)=0.3)。
(8)αi(t):(阿爾法)在給定馬爾可夫模型中,到t時刻為止,狀態們在t個時刻,每個時刻都由所有狀態中的一個輸出某個觀測值,一共輸出了t個觀測值觀測序列,記為,
,並且t時刻輸出Ot的狀態為qi(狀態用q表示),把出現上述場景的概率記作αi(t),稱作前向概率(應該是在做前向計算,所以形象成為」前向概率「)。
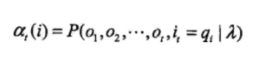
(9)aij:(字母a,注意不是阿爾法,在第一張圖中的「推導」公式裏面的)概率轉移矩陣中第i行,第j列對應的概率(今天為第i個狀態,明天為第j個狀態的概率。網絡圖示中「吃->吃」、「吃->睡」和「睡->睡」之間連線的數 值)。
(10)轉移概率矩陣:如下圖A所示。

理解
 :
:
表示第1時刻,第i個狀態的初始概率Πi乘以第i個狀態對應的輸出矩陣的第i行向量。
例如:假設第i個狀態為「睡」,那麼Πi等於0.7,bi等於[0.3,0.5,0.2],那麼第1時刻的狀態為「睡」,觀測值為「哭」、「沒精神」和「找媽媽」的概率分別為0.7*[0.3,0.5,0.2],如果第一時刻的觀測值為「哭」,那麼α1(t)=0.21.
![]() :
:
t+1時刻,所有t時刻的前向概率裏面按時的t時刻的狀態轉化為j狀態後再乘以j對應的輸出概率總和。
以第2時刻為例:狀態j為「吃」,那麼αj(t+1)表示第二時刻,第二狀態為「吃」,觀測值序列為的O1O2概率,其等於第1時刻的前向概率αi(t) 乘以 第一時刻的前向概率裏面暗示的第一時刻的狀態i轉化為狀態j的概率(aij),i有可能是「吃」,也有可能是「睡」,我們要計算的是第2時刻狀態為「吃」的概率,根據馬爾可夫模型,第二時刻的「吃」和第一時刻的狀態有關,但是我們不知道第一時刻到底是什麼狀態,所以用概率的方式全部考慮進來。
[0.21,0.03,0.02]*0.1*bjo2(0.1表示「吃1」->「吃2」的概率)+[0.21,0.15,0.14]*0.9*bjo2(0.9表示「睡1」->「吃2」的概率)
乘上轉移概率之後,在乘以「吃」對應的輸出概率行向量:
[0.021,0.003,0.002]Tx[0.7,0.1,0.2] + [0.189,0.135,0.126]Tx[0.7,0.1,0.2](考慮了所有情況,可能會有點費解,請看下一行)
如果第一時刻的觀測值為「哭」,第二時刻的狀態為「吃」,觀測值為「哭」,那麼αj(t+1)=0.21*0.1*0.7=0.0147 + 0.21*.0.9*0.7=0.1323.
 :
:
μ:給定的馬爾可夫模型。
O:1-T+1時刻的觀測值序列。
在馬爾可夫模型μ中,輸出序列O的概率為:輸出O並且T+1時刻的狀態為qi的概率綜合。
本文截圖部分來自:隱馬爾科夫模型(HMM)一前向與後向算法 – 知乎 (zhihu.com)


