Non-local Network:人類早期在CV馴服Transformer嘗試 | CVPR 2018
Non-local操作是早期self-attention在視覺任務上的嘗試,核心在於依照相似度加權其它特徵對當前特徵進行增強,實現方式十分簡潔,為後續的很多相關研究提供了參考
來源:曉飛的算法工程筆記 公眾號
論文: Non-local Neural Networks

Introduction

卷積操作通常在局部區域進行特徵提取,想要獲取範圍更廣的特徵信息需要重複進行卷積操作來獲得,這樣不僅耗時還增加了訓練難度。為此,論文提出高效的non-local操作,將特徵圖上的特徵點表示為所有特徵點的加權和,用於捕捉覆蓋範圍更廣的特徵信息。non-local操作也可以用於含時序的任務中,如圖1的視頻分類任務,可綜合幾幀的特徵來增強當前幀的特徵。
non-local操作主要有以下優點:
- 相對於疊加卷積的操作,non-local可通過特徵點間的交互直接捕捉更廣的特徵信息。
- 從實驗結果來看,簡單地嵌入幾層non-local操作就能高效地提升網絡性能。
- non-local操作支持可變輸入,可很好地與其它網絡算子配合。
Non-local Neural Networks
Formulation
首先定義通用的non-local操作:

i為特徵圖上將要計算特徵值的位置坐標,j為特徵圖上的所有位置坐標,x為對應位置上的輸入特徵,y為增強後的輸出,f計算i和j之間的相似性,g則用於對j的特徵進行轉化,\mathcal{C}用於對輸出進行歸一化。
簡而言之,non-local的核心就是計算當前位置的特徵與特徵圖所有特徵間的相似性,然後根據相似性對所有特徵加權輸出。相對於卷積和全連接等參數固定的操作,non-local更加靈活。
Instantiations
在實現時,函數f和函數g的選擇很多。為了簡便,函數g選擇為線性變換g(x_j)=W_gx_j,W_g為可學習的權重矩陣,一般為$1\times 1的卷積。而函數f則可以有以下選擇(論文通過實驗發現函數f$的具體實現影響不大):
-
Gaussian

x^T_i x_j為點積相似度,也可採用歐氏距離,\mathcal{C}(x)={\sum}_{\forall j}f(x_i, x_j),歸一化類似於softmax操作。
-
Embedded Gaussian
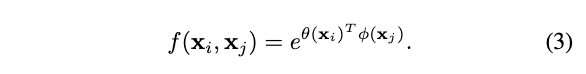
\theta(x_i)=W_{\theta}x_i和\phi(x_j)=W_{\phi}x_j為兩個線性變換,\mathcal{C}(x)={\sum}_{\forall j}f(x_i, x_j),這個實現與self-attention十分接近。
-
Dot product

先線性變換,然後通過點積計算相似度,\mathcal{C}(x)=N,有助於簡化梯度計算。
-
Concatenation

直接將特徵conate起來,通過權重向量w^T_f轉化為標量輸出,\mathcal{C}(x)=N。
Non-local Block
將公式1的non-local操作修改成non-local block,可插入到當前的網絡架構中,non-local block的定義為:

公式6將non-local操作的輸出線性變換後與原特徵進行相加,類似於residual block的嵌入方式。
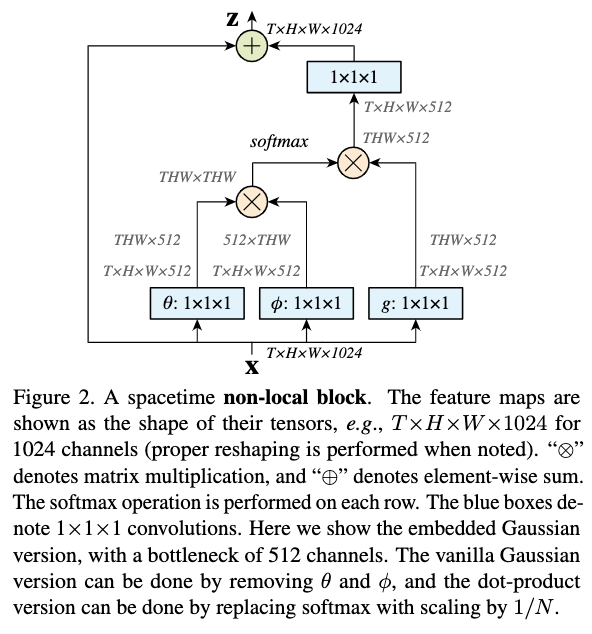
non-local block的一種實現方式如圖2所示,首先對x進行3種不同的線性變換,然後按照公式1得到輸出特徵,再與原特徵進行相加,基本上跟self-attention是一樣的。
Experiment

各種對比實驗,表2a為函數f的實現對比,可以看到影響不是很大。

視頻分類對比。

COCO上的分割、檢測、關鍵點對比。
Conclusion
Non-local操作是早期self-attention在視覺任務上的嘗試,核心在於依照相似度加權其它特徵對當前特徵進行增強,實現方式十分簡潔,為後續的很多相關研究提供了參考。
如果本文對你有幫助,麻煩點個贊或在看唄~
更多內容請關注 微信公眾號【曉飛的算法工程筆記】



