淺談歸併排序:合併 K 個升序鏈表的歸併解法
在面試中遇到了這道題:如何實現多個升序鏈表的合併。這是 LeetCode 上的一道原題,題目具體如下:
用歸併實現合併 K 個升序鏈表
給你一個鏈表數組,每個鏈表都已經按升序排列。
請你將所有鏈表合併到一個升序鏈表中,返回合併後的鏈表。
示例 1:
輸入:lists = [[1,4,5],[1,3,4],[2,6]] 輸出:[1,1,2,3,4,4,5,6] 解釋:鏈表數組如下: [ 1->4->5, 1->3->4, 2->6 ] 將它們合併到一個有序鏈表中得到。 1->1->2->3->4->4->5->6
這題可以用歸併的思想來實現,我們兩兩鏈表合併,到最後合成所有的鏈表。代碼如下:
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length - 1);
}
public ListNode merge(ListNode[] lists, int left, int right) {
if(left == right) {
return lists[left];
}
if (left > right) {
return null;
}
int mid = (left + right) >> 1;
return mergeTwoLists(merge(lists, left, mid), merge(lists, mid + 1, right));
}
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null) {
return l2;
}
if(l2 == null) {
return l1;
}
ListNode head = new ListNode(-1);
ListNode cur = head;
while(l1 != null && l2 != null) {
if(l1.val < l2.val) {
cur.next = l1;
l1 = l1.next;
}else {
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 == null ? l2:l1;
return head.next;
}
現在我們來回顧一下歸併排序的知識
一、歸併排序
1. 歸併排序的定義
- 基本思路:藉助外部空間,合併兩個有序數組/序列,得到更長的數組
- 算法思想:分而治之
比如對於數組[8,4,5,7,1,3,6,2]的排序:整體的過程是這樣:先「分」成小問題,再進行「治」操作
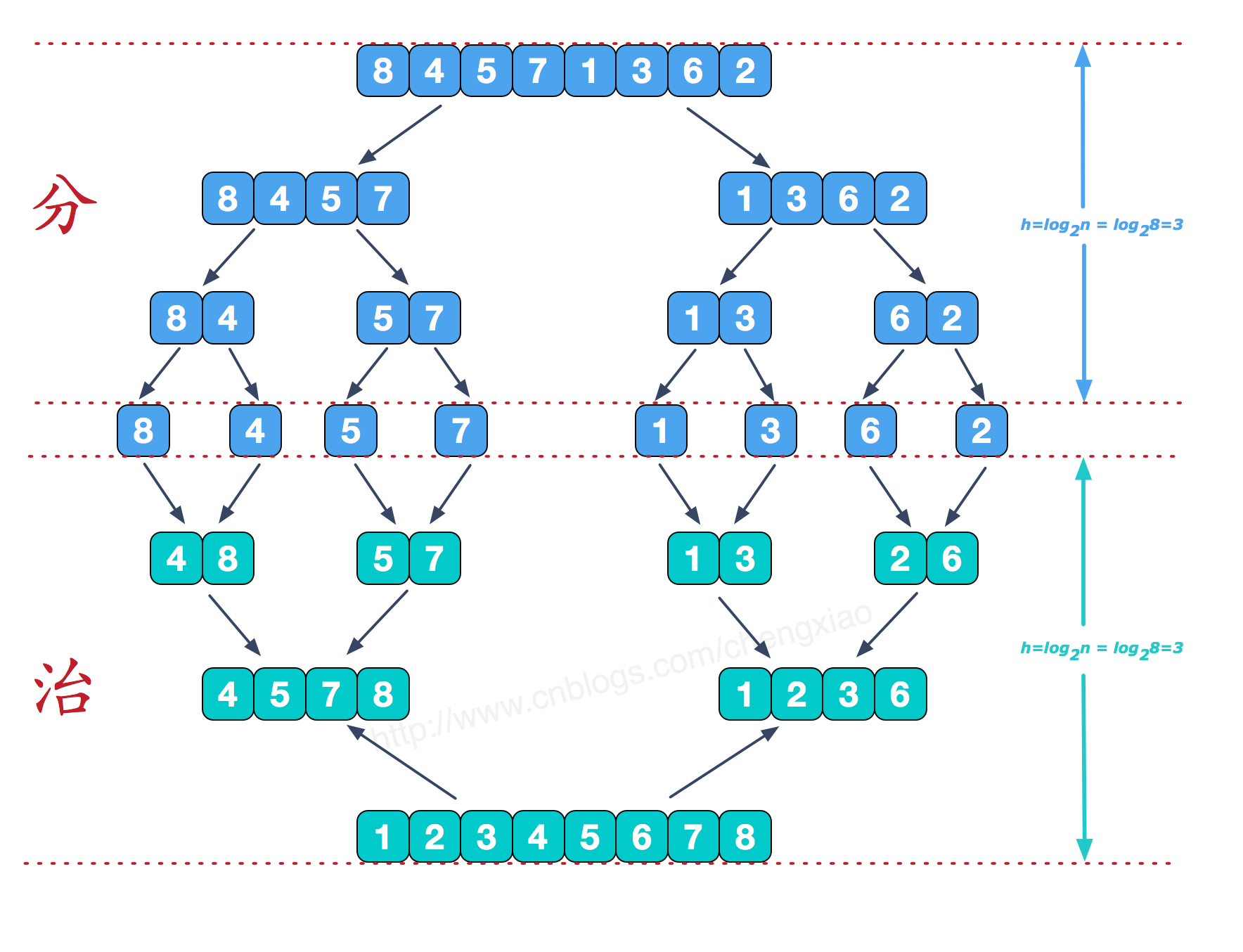
2.歸併排序算法代碼實現
先來看看歸併排序實現一個數組[8,4,5,7,1,3,6,2]的排序,難以理解的是合併相鄰有序子序列這塊,我們來看 [4,5,7,8] 和[1,2,3,6]這兩個已經有序的子序列的合併:圖片轉自這篇博客圖解排序算法(四)之歸併排序
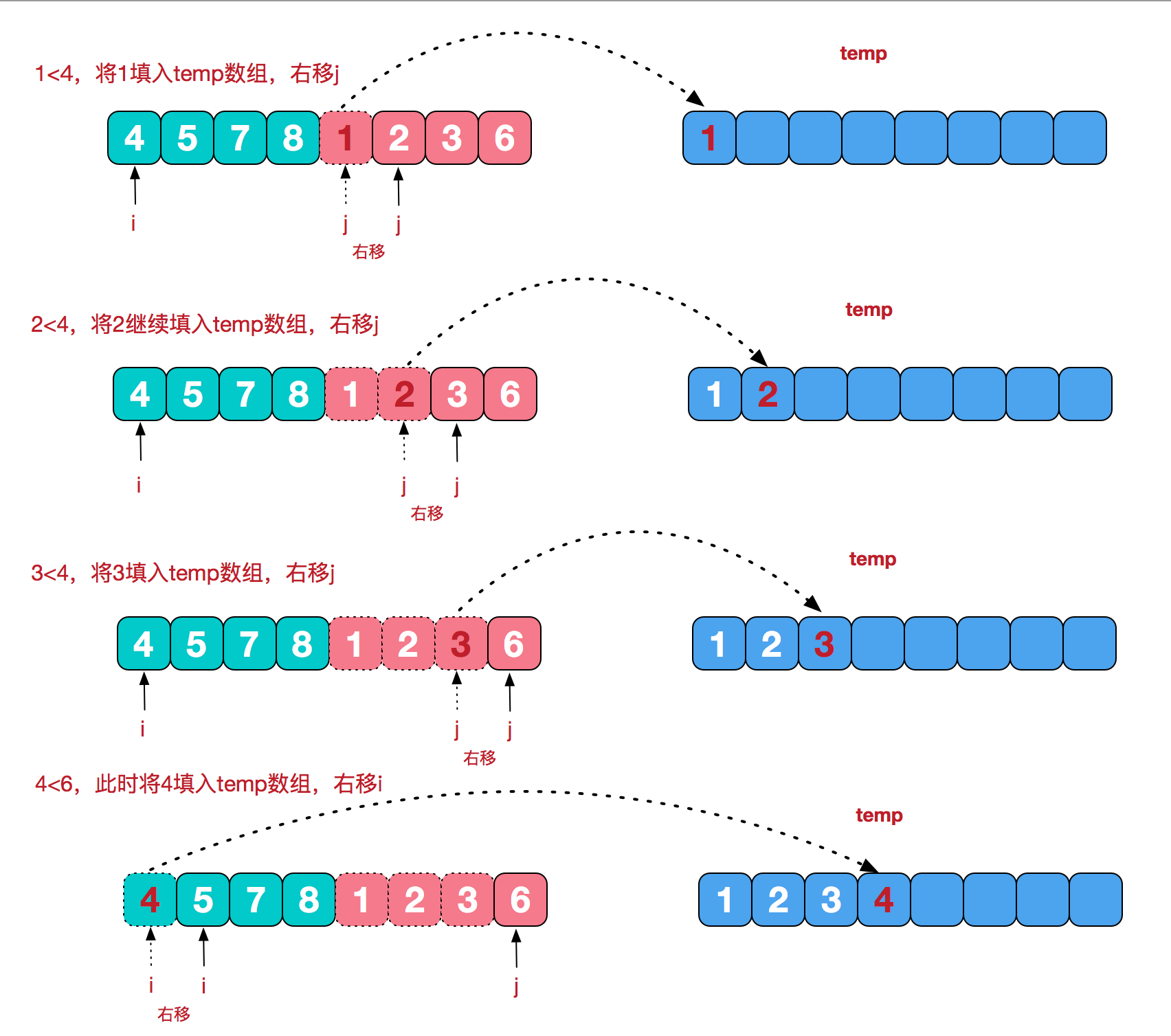
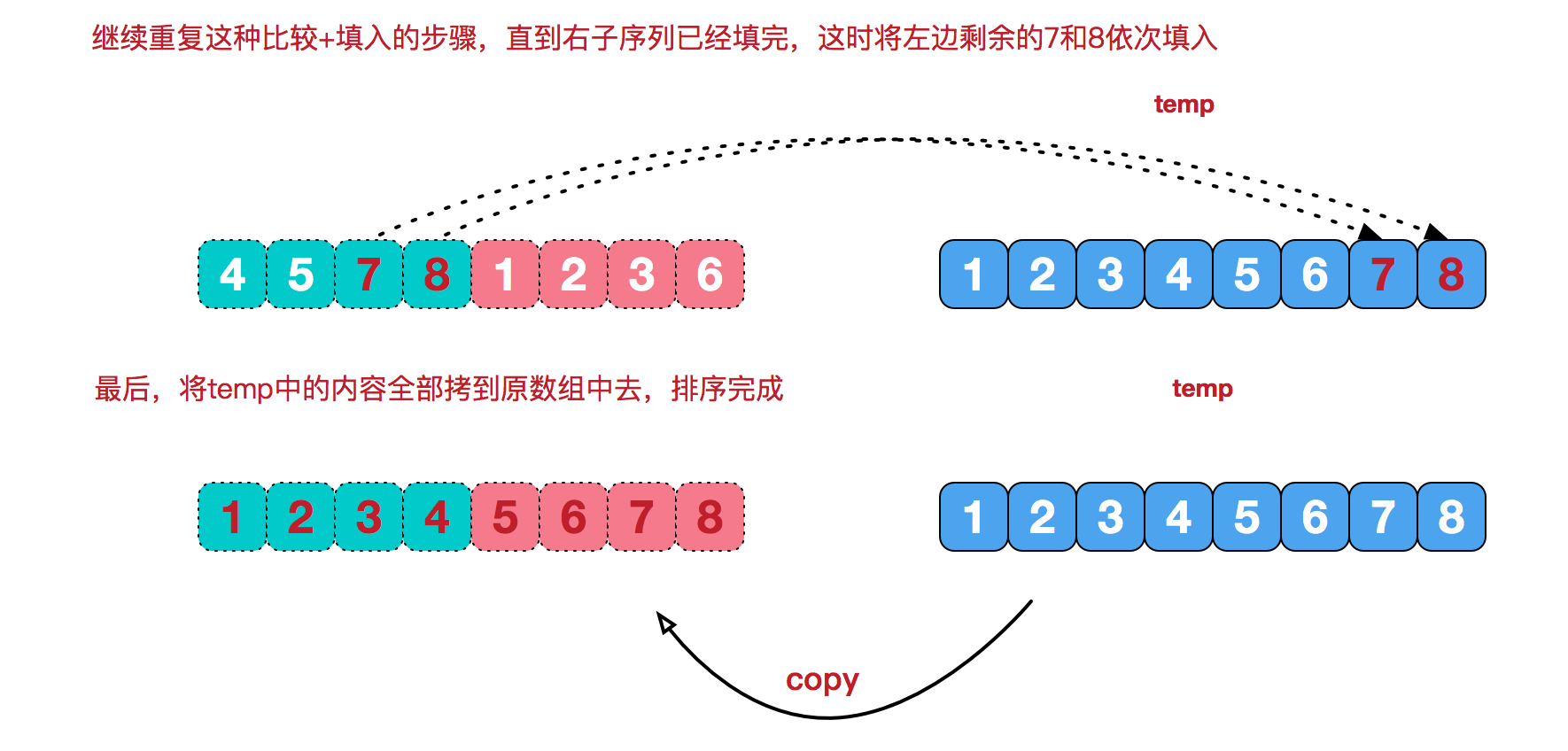
public int[] sortArray(int[] nums) {
int[] temp = new int[nums.length];
merge(nums, 0, nums.length - 1, temp);
return nums;
}
public void merge(int[] nums, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) >> 1;
merge(nums, left, mid, temp);
merge(nums, mid + 1, right, temp);
mergeSort(nums, left, mid, right, temp);
}
}
public void mergeSort(int[] nums, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
for(int k = left; k <= right; k++) {
temp[k] = nums[k];
}
for(int k = left; k <= right; k++) {
//當 i 指針走完時,將 j 指針部分複製到數組中
if(i == mid +1) {
nums[k] = temp[j];
j++;
//若 j 指針走完,將 i 指針部分複製到最後數組中
}else if(j == right + 1) {
nums[k] = temp[i];
i++;
//這裡的 = 是保持排序算法的穩定性,即排序後相等的數據原有順序不變
}else if(temp[i] <= temp[j]) {
nums[k] = temp[i];
i++;
}else {
nums[k] = temp[j];
j++;
}
}
}
二、歸併排序的一些經典題
1.LeetCode 88. 合併兩個有序數組
給你兩個按 非遞減順序 排列的整數數組 nums1 和 nums2,另有兩個整數 m 和 n ,分別表示 nums1 和 nums2 中的元素數目。
請你 合併 nums2 到 nums1 中,使合併後的數組同樣按 非遞減順序 排列。
注意:最終,合併後數組不應由函數返回,而是存儲在數組 nums1 中。為了應對這種情況,nums1 的初始長度為 m + n,其中前 m 個元素表示應合併的元素,後 n 個元素為 0 ,應忽略。nums2 的長度為 n 。
示例 1:
輸入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
輸出:[1,2,2,3,5,6]
解釋:需要合併 [1,2,3] 和 [2,5,6] 。
合併結果是 [1,2,2,3,5,6] ,其中斜體加粗標註的為 nums1 中的元素。
這道題可以用歸併排序的思想來完成,這裡就是用的「治」操作:
public void merge(int[] nums1, int m, int[] nums2, int n) {
int[] temp = new int[m+n];
for(int t = 0; t < m; t++) {
temp[t] = nums1[t];
}
for(int t = m, g = 0; t < m + n & g < n; t++,g++) {
temp[t] = nums2[g];
}
int i = 0;
int j = m;
for(int k = 0; k < m + n; k++) {
if(i == m) {
nums1[k] = temp[j];
j++;
} else if(j == m + n) {
nums1[k] = temp[i];
i++;
} else if(temp[i] <= temp[j]) {
nums1[k] = temp[i];
i++;
} else {
nums1[k] = temp[j];
j++;
}
}
}
2.劍指 Offer 51. 數組中的逆序對
在數組中的兩個數字,如果前面一個數字大於後面的數字,則這兩個數字組成一個逆序對。輸入一個數組,求出這個數組中的逆序對的總數。
示例 1:
輸入: [7,5,6,4]
輸出: 5
這題實際上還是利用數組中的元素兩兩配對比較,也就是分治處理,不過這次是比較大小後的計數。
public int reversePairs(int[] nums) {
int len = nums.length;
if(len < 2) {
return 0;
}
int[] temp = new int[len];
return mergePairs(nums, 0, len - 1, temp);
}
public int mergePairs(int[] nums, int left, int right, int[] temp) {
//如果是無參void 則可寫成 return; 或者不寫
if(left >= right) {
return 0;
}
int mid = (left + right) >> 1;
int leftCount = mergePairs(nums, left, mid, temp);
int rightCount = mergePairs(nums, mid + 1, right, temp);
int reverseCount = merge(nums, left, mid, right, temp);
//最後記得返回三者之和
return leftCount + rightCount + reverseCount;
}
public int merge(int[] nums, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
int count = 0;
for(int t = left; t <= right; t++) {
temp[t] = nums[t];
}
for(int k = left; k <= right; k++) {
if(i == mid + 1) {
nums[k] = temp[j++];
} else if(j == right + 1 || temp[i] <= temp[j]) {
nums[k] = temp[i++];
} else {
nums[k] = temp[j++];
count += mid - i + 1;
}
}
return count;
}
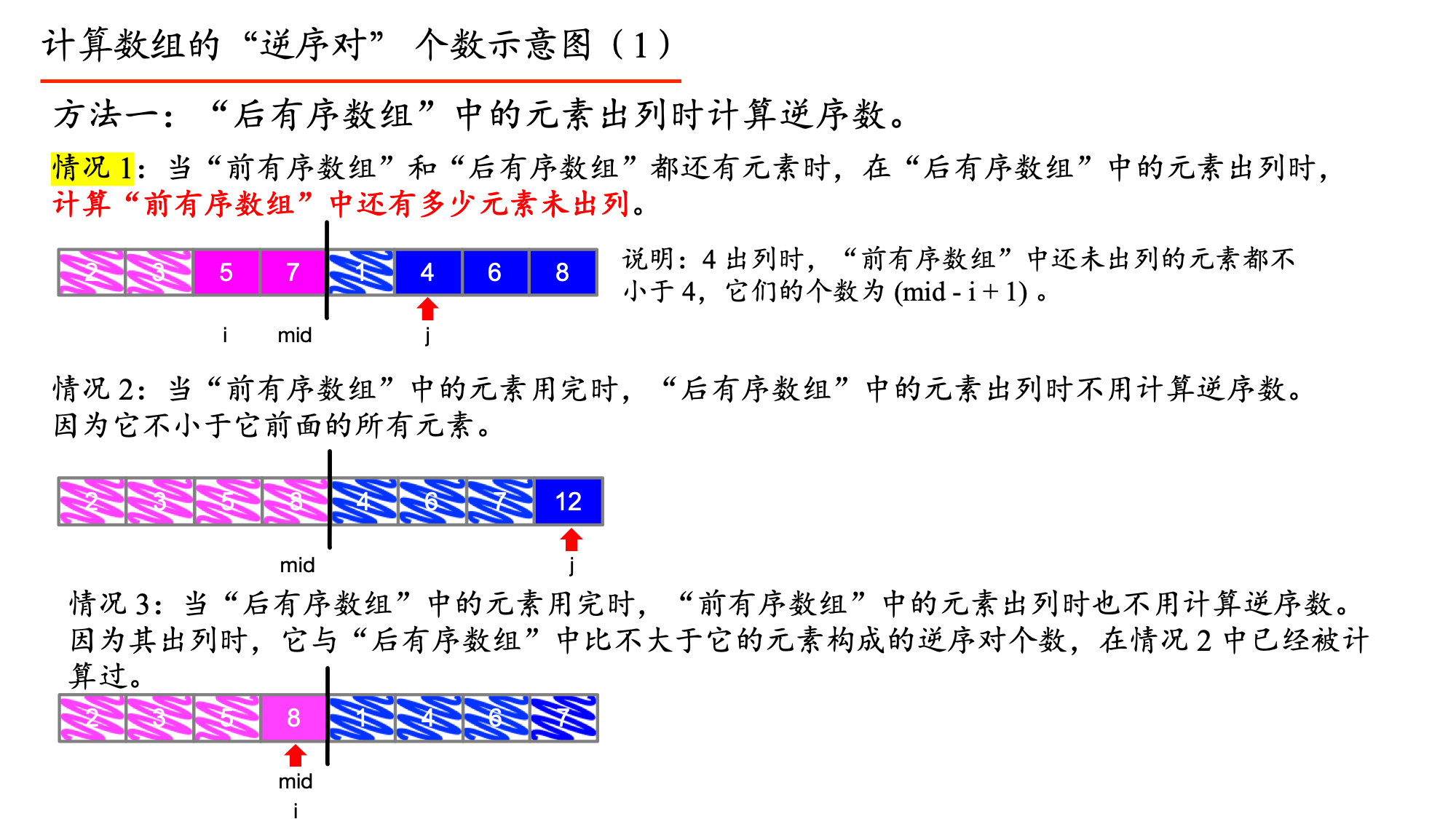
這裡要說一下逆序數的求法:前提是兩個序列有序
如果有兩個有序序列:
Seq1:3 4 5
Seq2:2 6 8 9
對於序列seq1中的某個數a[i],序列seq2中的某個數a[j]:
- 如果a[i]<a[j],沒有逆序數
- 如果a[i]>a[j],那麼逆序數為seq1 中a[i]後邊元素的個數(包括a[i]),即len1 -i+1。
3.LeetCode 315. 計算右側小於當前元素的個數
給你一個整數數組 nums ,按要求返回一個新數組 counts 。數組 counts 有該性質: counts[i] 的值是 nums[i] 右側小於 nums[i] 的元素的數量。
示例 1:
輸入:nums = [5,2,6,1] 輸出:[2,1,1,0] 解釋: 5 的右側有 2 個更小的元素 (2 和 1) 2 的右側僅有 1 個更小的元素 (1) 6 的右側有 1 個更小的元素 (1) 1 的右側有 0 個更小的元素
這題和第二題類似,但是這裡要解決定位的問題,因為我們的元素節點在歸併排序的時候是會移動的,所以需要設置一個索引數組來給這些元素定位。但是求逆序數用的是第二種方法:在前有序數組出列時,計算後有序數組中已經出列的元素個數。

public List<Integer> countSmaller(int[] nums) {
int len = nums.length;
List<Integer> res = new ArrayList<>();
if(len < 2) {
res.add(0);
return res;
}
int[] temp = new int[len];
int[] indexes = new int[len];
int[] result = new int[len];
for(int i = 0; i < len; i++) {
indexes[i] = i;
}
merge(nums, 0, len - 1, temp, indexes, result);
for(int i = 0; i < len; i++) {
res.add(result[i]);
}
return res;
}
public void merge(int[] nums, int left, int right, int[] temp, int[] indexes, int[] result) {
if(left >= right) {
return;
}
int mid = (left + right) >> 1;
merge(nums,left, mid, temp,indexes,result);
merge(nums,mid+1,right,temp,indexes,result);
mergeSort(nums,left,right,mid,temp,indexes,result);
}
public void mergeSort(int[] nums, int left, int right, int mid, int[] temp, int[] indexes, int[] result) {
int i = left;
int j = mid + 1;
for(int t = left; t <= right; t++) {
temp[t] = indexes[t];
}
for(int k = left; k <= right; k++) {
if(i == mid + 1) {
indexes[k] = temp[j++];
} else if(j == right + 1) {
indexes[k] = temp[i++];
result[indexes[k]] += right - mid;
} else if(nums[temp[i]] <= nums[temp[j]]) {
indexes[k] = temp[i++];
result[indexes[k]] += j - mid - 1;
} else {
indexes[k] = temp[j++];
}
}
}
歸併排序的思想很重要,在解決負責問題的分治思想有利於將大問題分解。從而更快的解決問題。
參考資料
//www.cnblogs.com/chengxiao/p/6194356.html


