看動畫學算法之:二叉搜索樹BST
簡介
樹是類似於鏈表的數據結構,和鏈表的線性結構不同的是,樹是具有層次結構的非線性的數據結構。
樹是由很多個節點組成的,每個節點可以指向很多個節點。
如果一個樹中的每個節點都只有0,1,2個子節點的話,這顆樹就被稱為二叉樹,如果我們對二叉樹進行一定的排序。
比如,對於二叉樹中的每個節點,如果左子樹節點的元素都小於根節點,而右子樹的節點的元素都大於根節點,那麼這樣的樹被叫做二叉搜索樹(Binary Search Tree)簡稱BST。
今天我們來探討一下BST的性質和對BST的基本操作。
BST的基本性質
剛剛我們已經講過BST的基本特徵了,現在我們再來總結一下:
- BST中任意節點的左子樹一定要比該節點的值要小
- BST中任意節點的右子樹一定要比該節點的值要大
- BST中任意節點的左右子樹一定要是一個BST。
看一張圖直觀的感受一下BST:
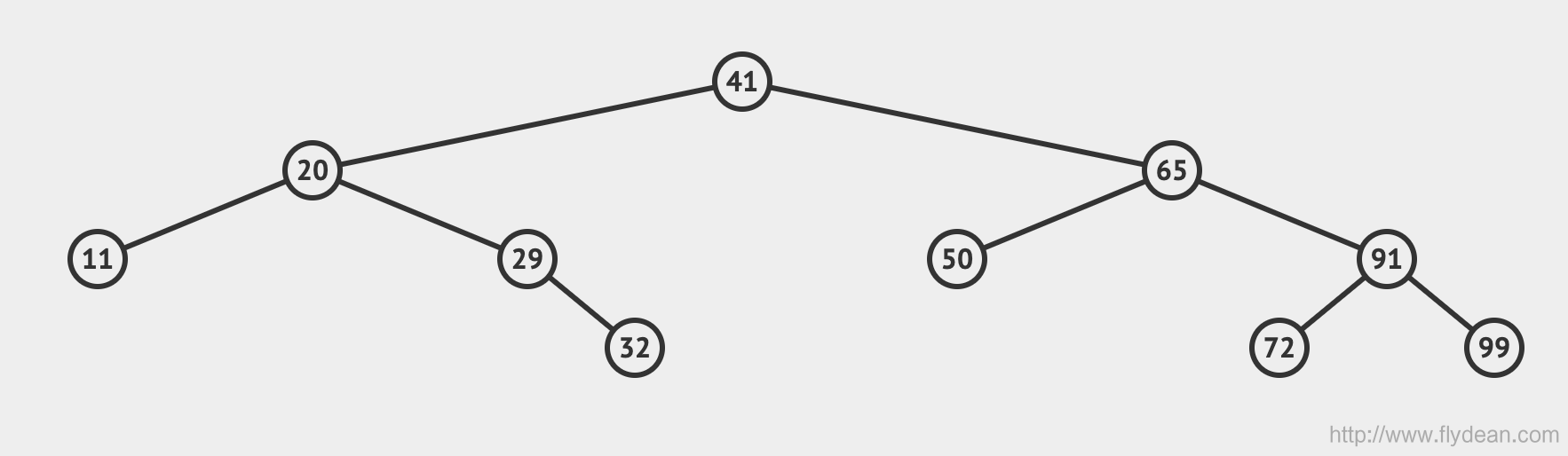
BST的構建
怎麼用代碼來構建一個BST呢?
首先,BST是由一個一個的節點Node組成的,Node節點除了保存節點的數據之外,還需要指向左右兩個子節點,這樣我們的BST完全可以由Node連接而成。
另外我們還需要一個root節點來表示BST的根節點。
相應的代碼如下:
public class BinarySearchTree {
//根節點
Node root;
class Node {
int data;
Node left;
Node right;
public Node(int data) {
this.data = data;
left = right = null;
}
}
}
BST的搜索
先看下BST的搜索,如果是上面的BST,我們想搜索32這個節點應該是什麼樣的步驟呢?
先上圖:
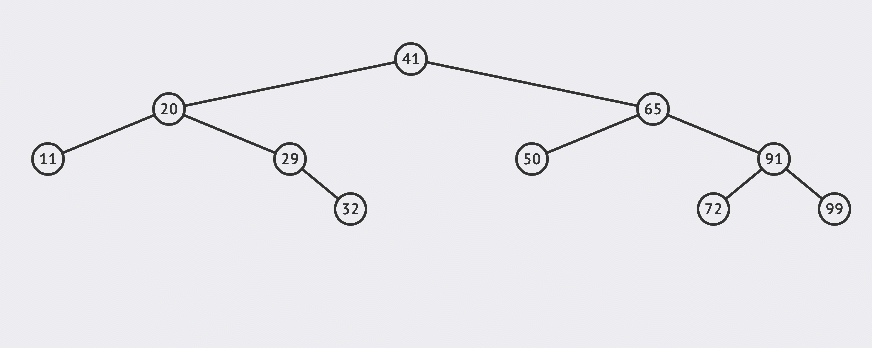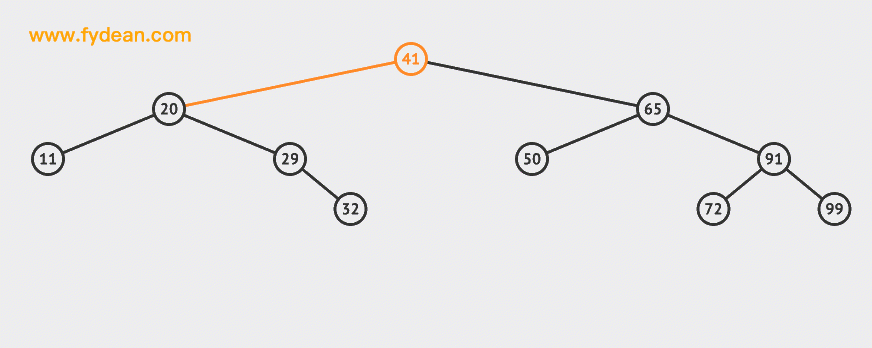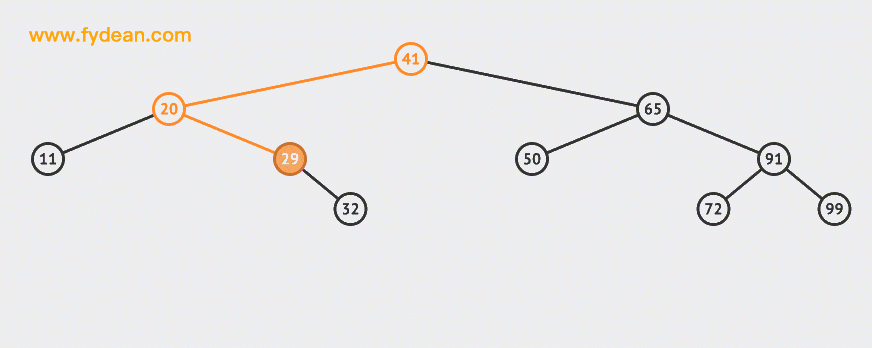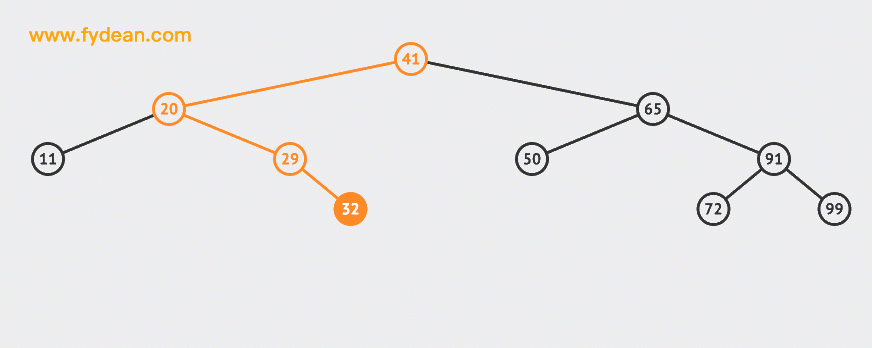
搜索的基本步驟是:
- 從根節點41出發,比較根節點和搜索值的大小
- 如果搜索值小於節點值,那麼遞歸搜索左側樹
- 如果搜索值大於節點值,那麼遞歸搜索右側樹
- 如果節點匹配,則直接返回即可。
相應的java代碼如下:
//搜索方法,默認從根節點搜索
public Node search(int data){
return search(root,data);
}
//遞歸搜索節點
private Node search(Node node, int data)
{
// 如果節點匹配,則返回節點
if (node==null || node.data==data)
return node;
// 節點數據大於要搜索的數據,則繼續搜索左邊節點
if (node.data > data)
return search(node.left, data);
// 如果節點數據小於要搜素的數據,則繼續搜索右邊節點
return search(node.right, data);
}
BST的插入
搜索講完了,我們再講BST的插入。
先看一個動畫:
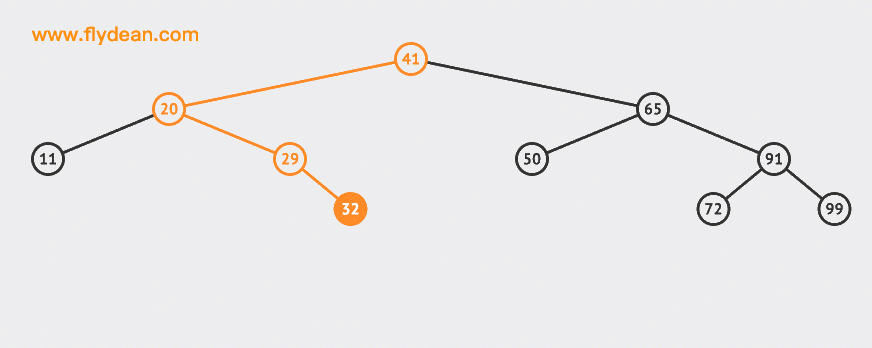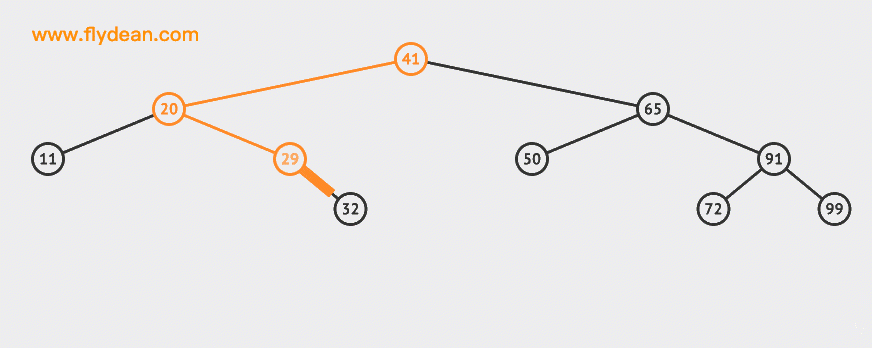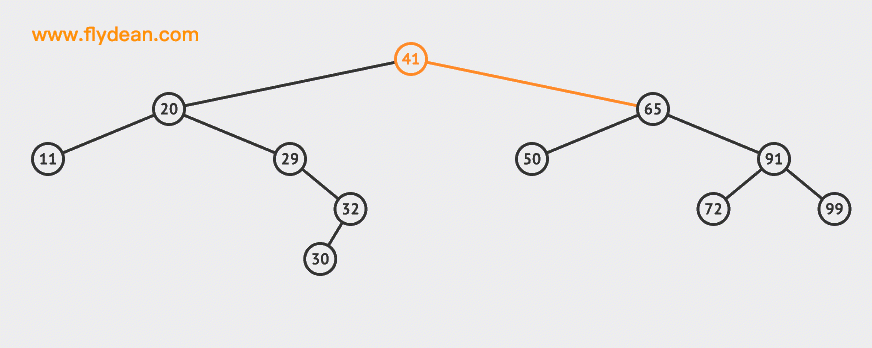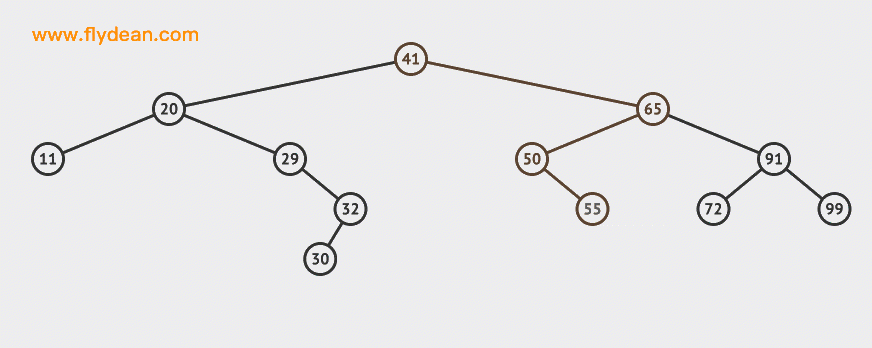
上的例子中,我們向BST中插入兩個節點30和55。
插入的邏輯是這樣的:
- 從根節點出發,比較節點數據和要插入的數據
- 如果要插入的數據小於節點數據,則遞歸左子樹插入
- 如果要插入的數據大於節點數據,則遞歸右子樹插入
- 如果根節點為空,則插入當前數據作為根節點
相應的java代碼如下:
// 插入新節點,從根節點開始插入
public void insert(int data) {
root = insert(root, data);
}
//遞歸插入新節點
private Node insert(Node node, int data) {
//如果節點為空,則創建新的節點
if (node == null) {
node = new Node(data);
return node;
}
//節點不為空,則進行比較,從而遞歸進行左側插入或者右側插入
if (data < node.data)
node.left = insert(node.left, data);
else if (data > node.data)
node.right = insert(node.right, data);
//返回插入後的節點
return node;
}
BST的刪除
BST的刪除要比插入複雜一點,因為插入總是插入到葉子節點,而刪除可能刪除的是非葉子節點。
我們先看一個刪除葉子節點的例子:
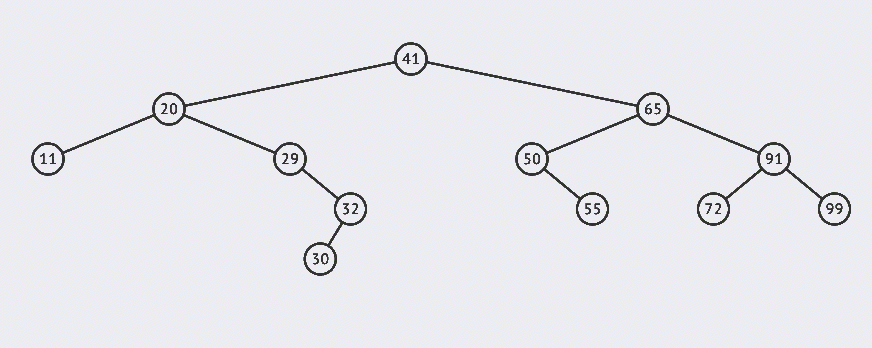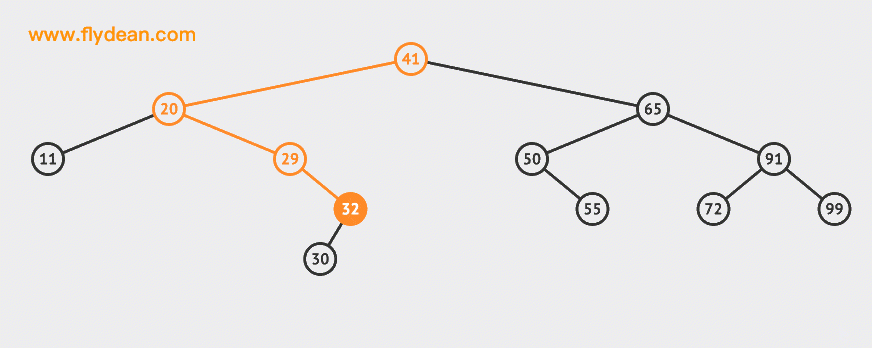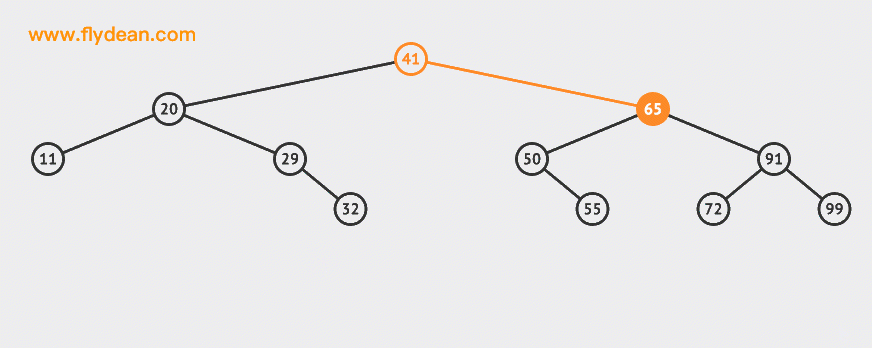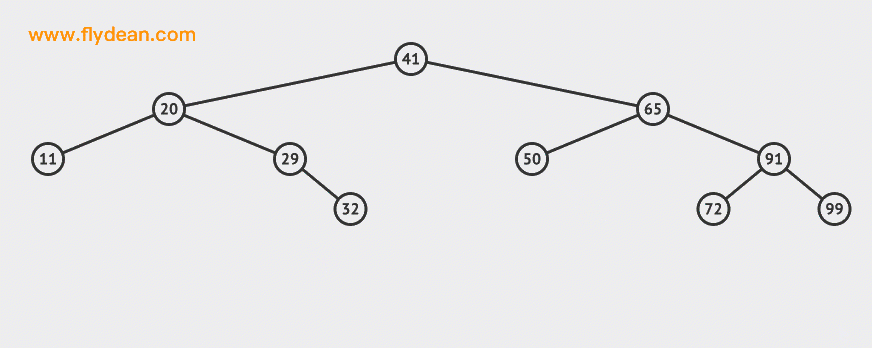
上面的例子中,我們刪除了30和55這兩個節點。
可以看到,刪除葉子節點是相對簡單的,找到之後刪除即可。
我們再來看一個比較複雜的例子,比如我們要刪除65這個節點:
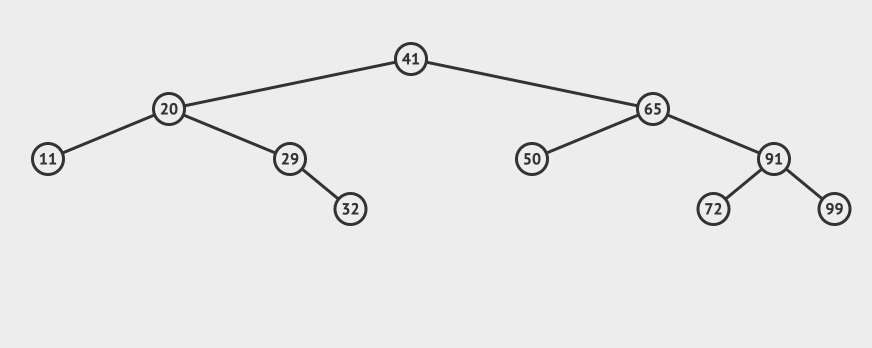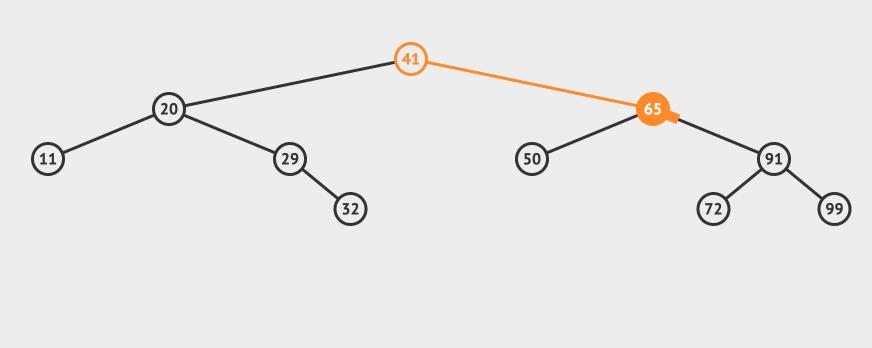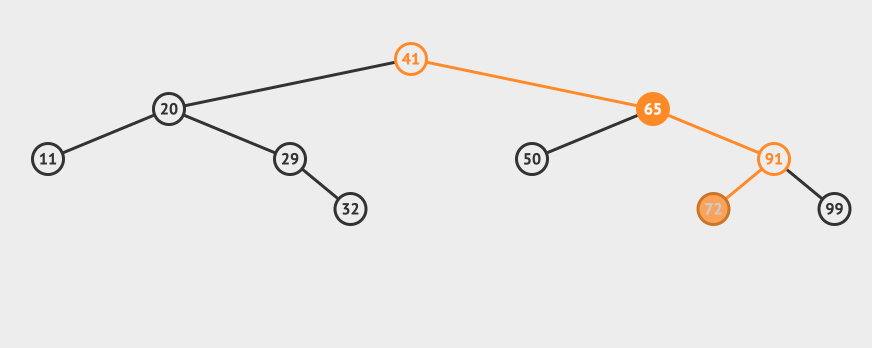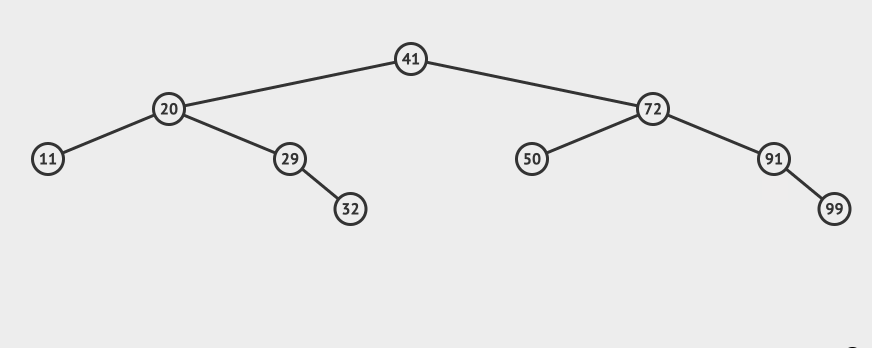
可以看到需要找到65這個節點的右子樹中最小的那個,替換掉65這個節點即可(當然也可以找到左子樹中最大的那個)。
所以刪除邏輯是這樣的:
- 從根節點開始,比較要刪除節點和根節點的大小
- 如果要刪除節點比根節點小,則遞歸刪除左子樹
- 如果要刪除節點比根節點大,則遞歸刪除右子樹
- 如果節點匹配,又有兩種情況
- 如果是單邊節點,直接返回節點的另外一邊
- 如果是雙邊節點,則先找出右邊最小的值,作為根節點,然後將刪除最小值過後的右邊的節點,作為根節點的右節點
看下代碼的實現:
// 刪除新節點,從根節點開始刪除
void delete(int data)
{
root = delete(root, data);
}
//遞歸刪除節點
Node delete(Node node, int data)
{
//如果節點為空,直接返回
if (node == null) return node;
//遍歷左右兩邊的節點
if (data < node.data)
node.left = delete(node.left, data);
else if (data > root.data)
node.right = delete(node.right, data);
//如果節點匹配
else
{
//如果是單邊節點,直接返回其下面的節點
if (node.left == null)
return node.right;
else if (node.right == null)
return node.left;
//如果是雙邊節點,則先找出右邊最小的值,作為根節點,然後將刪除最小值過後的右邊的節點,作為根節點的右節點
node.data = minValue(node.right);
// 從右邊刪除最小的節點
node.right = delete(node.right, node.data);
}
return node;
}
這裡我們使用遞歸來實現的刪除雙邊節點,大家可以考慮一下有沒有其他的方式來刪除呢?
本文的代碼地址:
本文收錄於 www.flydean.com
最通俗的解讀,最深刻的乾貨,最簡潔的教程,眾多你不知道的小技巧等你來發現!
歡迎關注我的公眾號:「程序那些事」,懂技術,更懂你!


