算法競賽——哈希表

一、哈希表介紹

什麼是哈希表？

散列表（Hash table，也叫哈希表），是根據鍵（Key）而直接訪問在內存存儲位置的數據結構。也就是說，它通過計算一個關於鍵值的函數，將所需查詢的數據映射到表中一個位置來訪問記錄，這加快了查找速度。這個映射函數稱做散列函數，存放記錄的數組稱做散列表。

哈希表有什麼用？

在 OI 中，最常見的情況應該是鍵值為整數的情況。當鍵值的範圍比較小的時候，可以直接把鍵值作為數組的下標，但當鍵值的範圍比較大，比如以 10^9範圍內的整數作為鍵值的時候，就需要用到哈希表。即把一個龐大的空間/值域）映射到一個較小的空間，0~10^9 ---> 0~10^5，即0 ~ N的一個數

二、哈希函數兩大操作

什麼是哈希函數？

要讓鍵值對應到內存中的位置，就要為鍵值計算索引，也就是計算這個數據應該放到哪裡。這個根據鍵值計算索引的函數就叫做哈希函數，也稱散列函數。

1.計算哈希函數

\[一般把鍵值模一個較大的質數（大於題目範圍的第一個質數）作為索引，也就是取f(x) \quad mod \quad N 作為哈希函數。
\]

2.解決衝突

如果對於任意的鍵值，哈希函數計算出來的索引都不相同，那隻用根據索引把 (key, value) 放到對應的位置就行了。但實際上，常常會出現兩個不同的鍵值，他們用哈希函數計算出來的索引是相同的。這時候就需要一些方法來處理衝突。在 OI 中，最常用的方法是拉鏈法和開放尋址法。

2.1.拉鏈法

拉鏈法是在每個存放數據的地方開一個鏈表，如果有多個鍵值索引到同一個地方，只用把他們都放到那個位置的鏈表裡就行了（鏈表的添加操作）。查詢的時候需要把對應位置的鏈表整個掃一遍，對其中的每個數據比較其鍵值與查詢的鍵值是否一致。

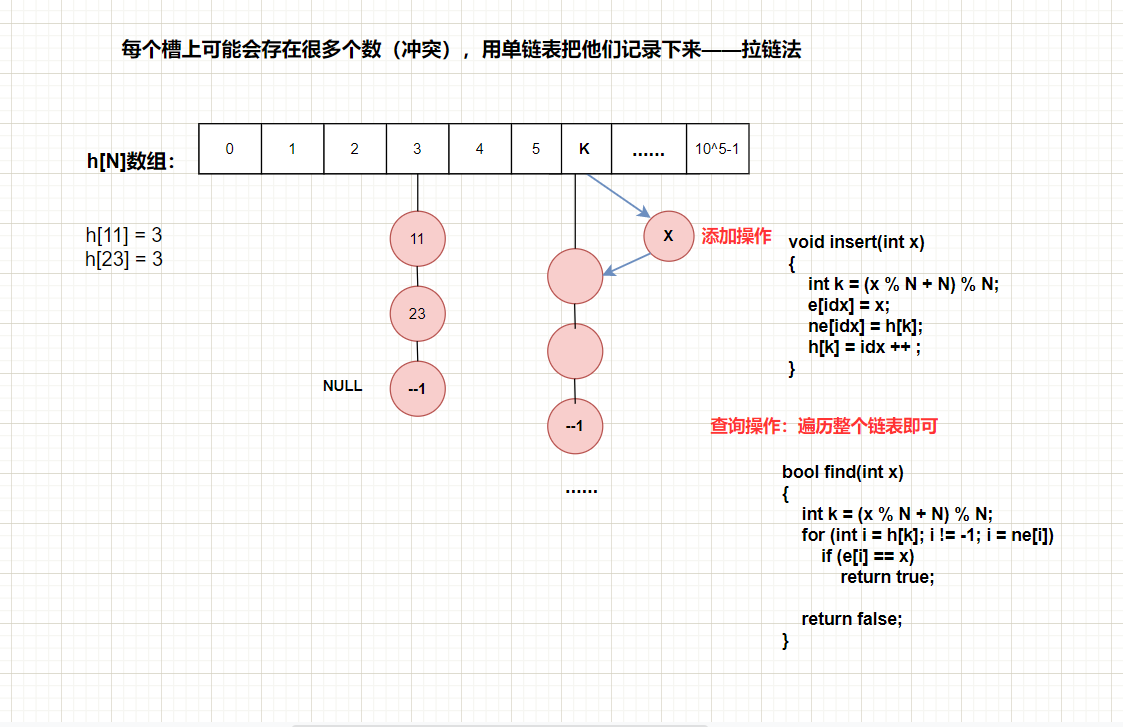
image

思路：利用鏈表處理衝突。輸入x，將x進行mod映射為k，然後h[k]作為鏈表的頭指針（相當於head記錄的是頭節點位置的下標），然後就是鏈表頭插法操作：e[idx] = x, ne[idx] = h[k], h[k] = idx ++;這樣就把新元素像拉鏈一樣掛在了h數組的下面了。尋找也是同理先求x的映射k，然後從h[k]開始鏈表的遍歷。當然，在main函數中記得要把h數組全部初始化為-1(空指針)。下圖為數組模擬單鏈表的頭插法操作：

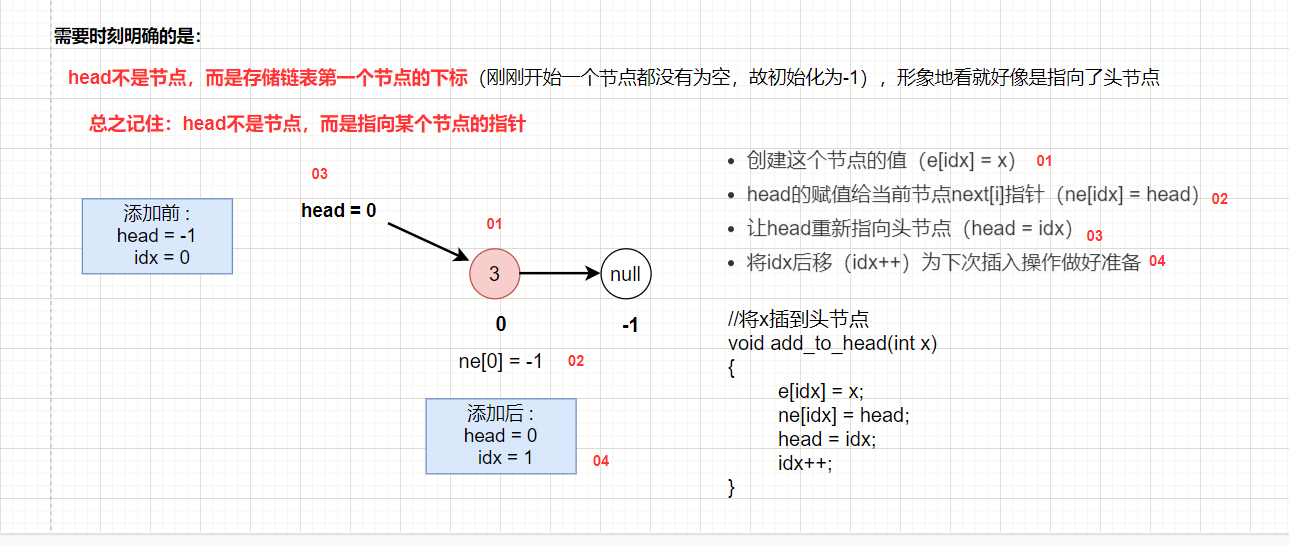
image

【拉鏈法——參考代碼】

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 3; // 大於10萬的第一個質數

int h[N];
int e[N], ne[N], idx; // idx表示當前用到了哪一個位置

// 頭插法，將x查到單鏈表h[k]的頭部————看之前模擬單鏈表的頭插法
 void insert(int x)
 {
     int k = (x % N + N) % N; // 將x映射成哈希值
     e[idx] = x;
// h[k]是hash之後下標為k的位置存放的idx(或者說指向的元素),之前原本h[]的所有值初始化為-1（head指向頭節點的指針（下標））     
     ne[idx] = h[k];
     h[k] = idx;
     idx ++;
     
 }
 
 bool find(int x)
 {
     int k = (x % N + N) % N;
     // 在k的鏈錶鏈表找是否存在X，h[k]即為指向頭節點的下標（指針）
     for(int i = h[k]; i != -1;i = ne[i])
        if(e[i] == x)
            return true;
            
    return false;
    
 }


int main()
{
    int n;
    cin >> n;
    
    // 千萬別忘了初始化，不然鏈表就沒有頭節點啦！
    memset(h, -1 , sizeof h); // 初始化鏈表，一開始為空：-1
    
    while (n -- )
    {
        string opt;
        int x;
        cin >> opt;
        if(opt == "I")
        {
            cin >> x;
            insert(x);
        }
        else 
        {
            cin >> x;
            if(find(x)) cout << "Yes" << endl;
            else cout << "No" << endl;
        }
    }

    return 0;
}

註：

h[N]相當於每個單鏈表的head指針。idx存儲當前用到了哪個節點，不同單鏈表裡的節點都是從idx這裡分配的，所以它們可以共用一個idx變量。之前原本h[]的所有值初始化為-1（head指向頭節點的指針）

【C++ STL】

#include<bits/stdc++.h>
using namespace std;
set<int>s;
char op;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int r;
        cin>>op>>r;
        if(op=='I')
            s.insert(r);
        else {
            if(s.find(r)==s.end())
                cout<<"No"<<endl;
            else cout<<"Yes"<<endl;
        }
    }
    return 0;
}

2.2.開放尋址法

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

// 數組長度一般開到個數上限的2-3倍。足夠存放，這樣大概率就沒有衝突了
// null 用來判斷當前槽位是否被使用過(不超過int範圍的無窮大的數)
//N 為大於範圍的第一個質數
const int N = 2e5 + 3, null = 0x3f3f3f3f;
int h[N];

int find(int x)
{
    int k = (x % N + N) % N;
   
    while(h[k] != null && h[k] != x) // 如果當前位置被佔了就往後找
    {
        k ++;
        if(k == N) k = 0; // 找到尾了，從頭再來
    }
    //返回：可以插入x的位置k，若位置k里已存在x直接返回k的位置
    return k;
}

int main()
{
    int n;
    cin >> n;
      memset(h, 0x3f, sizeof h); // 一開始所有槽全部初始化為null
    while (n -- )
    {
        string opt;
        int x;
        cin >> opt;
        if(opt == "I")
        {
            cin >> x;
            //找到x能夠插入的位置
            int k = find(x);
            h[k] = x;
        }
        else
        {
            cin >> x;
            //找x的位置看看是否存在
            int k = find(x);
            // 判斷h[]中是否存在x
            if(h[k] != null) cout << "Yes" << endl;
            else cout << "No" << endl;
        }
    }
    
    return 0;
}
開放尋址法總結
  1. memse是按位元組來初始化的，int中有四個位元組，初始化成0x3f就是將每個位元組都初始化成0x3f，所以每個int就是 0x3f3f3f3f。
  2. 數組長度一般開到個數上限的2-3倍。

三、memset總結**

memse是逐一位元組的進行初始的！

  • 使用memset初始化一定要慎重，一般只用來初始化0、-1、0x3f這幾個數字，其他的建議使用循環初始化，其他值盡量用for循環吧。
  • 作為無窮大，一個數除了要保證足夠大外，還要保證不能溢出。
    使用0x3f3f3f3f作為INF主要原因是，兩個0x3f3f3f3f的和只比int類型的最大值小一點，這樣既能保證一般情況下的足夠大，在兩個無窮相加時還能夠保證不會溢出。

四、整數哈希模板總結

拉鏈法：

// 拉鏈法
const int N = 大於範圍的第一個質數（先求一下）
int h[N], e[N], ne[N], idx;

// 插入x（頭插法——可以回顧之前數組模擬單鏈表的操作）
void insert(int x)
{
	int k = (x % N + N) % N;
	e[idx] = x;
	ne[idx] = h[k];
	h[k] = idx;
	idx ++;
}
// 查詢是否存在x
bool find(int x)
{
	int k = (x % N + N) % N;
	for(int i = h[k], i != -1; i = ne[i])
	{
		if(e[i] == x) return true;
	}
	
	return false;
}

註：千萬別忘記了初始化鏈槽數組h[]:memset(h, -1, sizeof h)

開放尋址法：

// 開放尋址法
const int N = 大於2~3倍範圍的第一個質數（先求一下）, null = 0x3f3f3f3f; // null用來判空
int h[N]; // 數組的長度一般開到範圍的2~3倍

// 尋找可以插入x的位置k/返回已存在x的位置k
int find(int x)
{
	int k = (x % N + N) % N;
	while(h[k] != null && h[k] != x)
	{
		k ++;
		if(k == N) k = 0;
	}
	
	return K;
}
註：千萬別忘記了初始化數組h[]:memset(h, 0x3f, sizeof h)

五、字符串哈希

(字符串哈希) O(n)+O(m)
全稱字符串前綴哈希法，把字符串變成一個p進制數字（哈希值），實現不同的字符串映射到不同的數字。

\[對形如 X1X2X3⋯Xn−1Xn 的字符串,採用字符的ascii 碼乘上 P 的次方來計算哈希值。

映射公式 (X1×Pn−1+X2×Pn−2+⋯+Xn−1×P1+Xn×P0)modQ
\]

注意事項：

  • 任意字符不可以映射成0，否則會出現不同的字符串都映射成0的情況，比如A,AA,AAA皆為0

  • \[衝突問題：通過巧妙設置P (131 或 13331) , Q (2^{64})的值，一般可以理解為不產生衝突。
    \]

typedef unsigned long long ULL，當溢出時等價於 mod 2^64方

字符串前綴哈希法的好處：

利用前綴哈希值就可以算出任一子段的哈希值！

【acwing 字符串哈希】

給定一個長度為n的字符串，再給定m個詢問，每個詢問包含四個整數l1,r1,l2,r2l1,r1,l2,r2，請你判斷[l1,r1l1,r1]和[l2,r2l2,r2]這兩個區間所包含的字符串子串是否完全相同。

字符串中只包含大小寫英文字母和數字。

輸入格式
第一行包含整數n和m，表示字符串長度和詢問次數。

第二行包含一個長度為n的字符串，字符串中只包含大小寫英文字母和數字。

接下來m行，每行包含四個整數l1,r1,l2,r2l1,r1,l2,r2，表示一次詢問所涉及的兩個區間。

注意，字符串的位置從1開始編號。

輸出格式
對於每個詢問輸出一個結果，如果兩個字符串子串完全相同則輸出「Yes」，否則輸出「No」。

每個結果佔一行。

數據範圍
1≤n,m≤1051≤n,m≤105
輸入樣例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
輸出樣例:
Yes
No
Yes

思路：

本題需要求到一個字符串中任意兩個區間的子串是否相同
可以轉換為求兩個區間子串的哈希值是否相等

\[前綴和公式 h[i]=h[i-1]×P+str[i] i∈[1,n] h為前綴和數組，str為字符串數組
\]

\[區間和公式 h[l,r]=h[r]−h[l−1]×Pr−l+1
\]

舉例說明：

“ABCDEFGHI”
123456789 (下標)
L R

字符串”A”的 哈希值為 p^0+A
字符串”AB” 哈希值為 p^1+A + p^0+B
字符串”ABC” 哈希值為 p^2+A + p^1+B + C
字符串[1,L-1]的哈希值為 p^3+A + p^2+B + p^1+C + p^0+D
字符串[1,R] 的哈希值為 p^8+A + p^7+B + … + P^0+I 從[1,L-1]每個數都多乘了 p^5（p^(R - L + 1)）

那麼如何求[L,R]字符串的哈希值呢，根據前綴和的思想，就是h[R] – h[L-1] (h[R]表示從[1,R]的字符串哈希值)
但是發現h[R]從[1,L-1]這一段left，每個數都比right這一段多乘了p^(R-(L-1))

所以字符串從[L,R]的哈希值為h[R] - h[L - 1] * p^(R-L+1)

【參考代碼】

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef unsigned long long ULL;//由於前綴值的值會很大 所以應該將數組中的數據定義為ULL型

const int N = 1e5 + 10, P = 131;// 註：這裡不能用p = 131（小寫——p代表p[]數組的首地址）

char str[N];
ULL h[N]; // h[i]表示前i個字符的哈希值（前綴哈希值）h[0] = 0
ULL p[N]; // p[i]表示p^i次方
int n, m;

// 計算子區間(l ~ r)的哈希值
int get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> str[i];
    
    p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i]; // 求前綴哈希值
        p[i] = p[i - 1] * P; // 計算p[i]
    }
    
    while (m -- )
    {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        
        if(get(l1, r1) == get(l2, r2)) puts("Yes");
        else puts("No");
    }
    
    return 0;
}

字符串前綴哈希法總結

`typedef unsigned long long ULL`，當溢出時等價於 mod 2^64方 ULL h[N],P[N]
衝突問題：通過巧妙設置或的值P=131/P=13331，一般可以理解為不產生衝突。
前綴和公式（前綴哈希值）：h[i] = h[i] * p + str[i];
區間和公式[l,r]的哈希值 = h[r] - h[l -1] * p[l - r + 1];

學習內容參考自：

1、[哈希表 – OI Wiki (oi-wiki.org)](//oi-wiki.org/ds/binary-heap/)

2、acwing算法基礎課

註：如果文章有任何錯誤或不足，請各位大佬盡情指出，評論留言留下您寶貴的建議！如果這篇文章對你有些許幫助，希望可愛親切的您點個贊推薦一手，非常感謝啦

Tags:

VirMach 便宜 VPS

QNews

QNews