論文解讀（DeepWalk）《DeepWalk: Online Learning of Social Representations》

• 2021 年 11 月 14 日
• 筆記
• 論文解讀

一、基本信息

論文題目：《DeepWalk: Online Learning of Social Representations》
發表時間：  KDD 2014
論文作者：  Bryan Perozzi、Rami Al-Rfou、Steven Skiena
論文地址：  //dl.acm.org/citation.cfm?id=2623732

二、前言

　　普通的鄰接矩陣在存儲的關係很多時，緯度將變得很高，而進行矩陣分解是一個相當費時複雜的過程，因此通過矩陣分解的方法進行網絡的表示學習，目前並沒有應用到大尺度數據集的方案。

　　本文通過將已經成熟的自然語言處理模型word2vec應用到網絡的表示上，做到了無需進行矩陣分解即可表示出網絡中的節點的關係。

　　DeepWalk把對圖中節點進行的一串隨機遊走類比於 word2vec 中對單詞的上下文，作為 word2vec 算法的輸入，進而把節點表示成向量。輸出的結果能夠被多種分類算法作為輸入應用。

三、介紹

　　Deepwalk：將一個網絡中的每個節點映射成一個低維的向量。說白了就是用一個向量去表示網絡中的每個節點，並且希望這些向量能夠將網絡中的節點中的關係表達出來，即希望在原始網絡中關係越緊密的結點對應的向量在其空間中距離越近。

　　輸入的是一個網絡，其中顏色相同的結點表示拓撲關係上更為相近的結點。輸出的是每個節點的二維向量，每個節點對應的向量關係如圖所示。我們可以從這個圖看出，越是拓撲結構相近的點，其對應的二維向量在二維空間上距離與近。

　　個人理解：可以將這個過程理解為一個降維的過程，但是不同於傳統意義上的高緯度降到低緯度，而是將一個複雜的結構降到低緯度。或者說可以理解為，將網絡中的拓撲結構，嵌入到一個低維向量中，每個節點的低維向量，從某種程度上反應了該節點在網絡中的連接情況。

　　我認為最主要的好處，就是便於將一些機器學習的算法應用到網絡中。網絡數據不同於傳統的數據，它不僅包含了節點的信息，還包含了節點間的關係，對於傳統的機器學習算法，很難將其應用於網絡中。例如網絡中的社團發現算法，大多數情況下我們都針對網絡做大量的遊走，不斷改變網絡的社團結構，以使網絡獲得最優的模塊度，但是如果我們能將拓撲信息嵌入到低維向量中，那麼每個節點我們都可以看做是一個樣本，每個維度都可以看做一個 feature，那麼只需要跑個聚類算法，就可以得到很好的結果。除了聚類，還有鏈路預測、推薦等一系列網絡中的問題，都可以直接扔到機器學習的相關算法中跑出來。

四、Problem definition

 　　　　$G_{L}=(V, E, X, Y) $

　　　　$X \in \mathbb{R}^{|V| \times S} \quad S \  is\  the\  size\  of\  feature\  space $

　　　　$E \subseteq(V \times V)$

　　　　$Y \in \mathbb{R}^{|V| \times|\mathcal{Y}|} \quad \mathcal{Y} \  is\  the\  size\  of\  labels\  set  $

　　輸入：一個圖的點集和邊集

　　輸出：對於一般的機器學習問題，需要學習一個從 $X$ 映射到 $Y$ 的 hypothesis。而本文的任務就是學習得到$X$ 的低維表示。

　　Goal：Our goal is to learn $X_{E} \in \mathbb{R}^{|V| \times d}$ , where d is small number of latent dimensions. These low-dimensional representations are distributed; meaning each social phenomena is expressed by a subset of the dimensions and each dimension contributes to a subset of the social concepts expressed by the space.

有意思的思考：

原文：

　　We propose a different approach to capture the network topology information. Instead of mixing the label space as part of the feature space,

we propose an unsupervised method which learns features that capture the graph structure independent of the labels』 distribution.

　　This separation between the structural representation and the labeling task avoids cascading errors, which can occur in iterative methods.

五、Learning social representations

　　文中提到，在學習一個網絡表示的時候需要注意的幾個性質：

• • Adaptability：網絡表示必須能適應網絡的變化。網絡是一個動態的圖，不斷地會有新的節點和邊添加進來，網絡表示需要適應網絡的正常演化。
  • Community aware：屬於同一個社區的節點有着類似的表示。網絡中往往會出現一些特徵相似的點構成的團狀結構，這些節點表示成向量後必須相似。
  • Low dimensional：代表每個頂點的向量維數不能過高，過高會有過擬合的風險，對網絡中有缺失數據的情況處理能力較差。
  • Continuous：低維的向量應該是連續的。

　　提到網絡嵌入，可能會讓人聯想到NLP中的word2vec，也就是詞嵌入(word embedding)。前者是將網絡中的節點用向量表示，後者是將單詞用向量表示。因為大多數機器學習的方法的輸入往往都是一個向量，算法也都基於對向量的處理，從而將不能直接處理的東西轉化成向量表示，這樣就能利用機器學習的方法對其分析，這是一種很自然的思想。

　　本文處理網絡節點的表示(node representation)就是利用了詞嵌入（詞向量）的的思想。詞嵌入的基本處理元素是單詞，對應網絡網絡節點的表示的處理元素是網絡節點；詞嵌入是對構成一個句子中單詞序列進行分析，那麼網絡節點的表示中節點構成的序列就是隨機遊走。

六、Random Walks

　　所謂隨機遊走(random walk)，就是在網絡上不斷重複地隨機選擇遊走路徑，最終形成一條貫穿網絡的路徑。從某個特定的端點開始，遊走的每一步都從與當前節點相連的邊中隨機選擇一條，沿着選定的邊移動到下一個頂點，不斷重複這個過程。

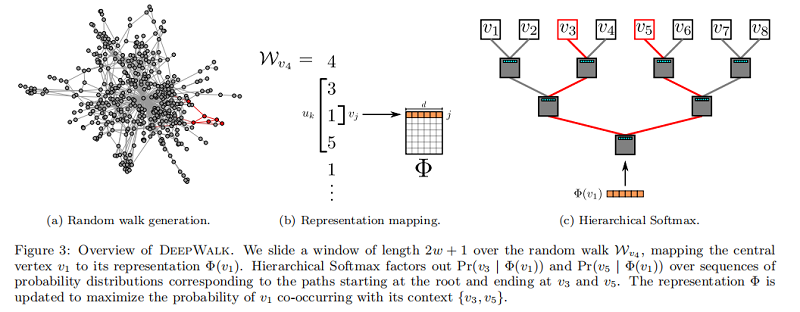
　　關於隨機斿走的符號解釋: 以  $v_{i}$  為根節點生成的一條隨機遊走路徑 (綠色) 為  $W_{v_{i}} $ ，其中路徑上的點 (藍色) 分別標記為  $W_{v_{i}}^{1}, W_{v_{i}}^{2}, W_{v_{i}}^{3} \ldots$ , 截斷䐈機遊走(truncated random walk)實 際上就是長度固定的隨機遊走。

使用隨機遊走有兩個好處：

• 並行化，隨機遊走是局部的，對於一個大的網絡來說，可以同時在不同的頂點開始進行一定長度的隨機遊走，多個隨機遊走同時進行，可以減少採樣的時間。
• 適應性，可以適應網絡局部的變化。網絡的演化通常是局部的點和邊的變化，這樣的變化只會對部分隨機遊走路徑產生影響，因此在網絡的演化過程中不需要每一次都重新計算整個網絡的隨機遊走。

七、Connection: Power laws

　　文中提到網絡中隨機遊走的分佈規律與NLP中句子序列在語料庫中出現的規律有着類似的冪律分佈特徵。那麼既然網絡的特性與自然語言處理中的特性十分類似，那麼就可以將NLP中詞向量的模型用在網絡表示中，這正是本文所做的工作。

八、語言模型

　　首先來看詞向量模型：
　　　　$w_{i}^{u}=\left(w_{0}, w_{1}, w_{2}, \ldots, w_{n}\right)$  是一個由若干單詞組成的序列，其中 $w_{i} \in V( Vocabulary )$，$V$  是詞彙表，也就是所有單詞組成的集合。
　　在整個訓練集上需要優化的目標是:

　　　　$\operatorname{Pr}\left(w_{n} \mid w_{0}, w_{1}, \ldots, w_{n}-1\right)$

　　也就是給定 $w_0,w_1,…….,w_{i-1}$ 要求出下一個 $w_{i}$ 出現的概率

　　將語言模型中的單詞映射到圖表示上去，單詞即對應了圖中的節點 $v_i$ ，句子序列對應了網絡中的隨機遊走，那麼對於一個隨機遊走$v_0,v_1,v_2,…….,v_{i-1}$需要優化的目標是：

　　$\operatorname{Pr}\left(v_{i} \mid\left(v_{0}, v_{1}, \ldots, v_{i-1}\right)\right)$

　　按照上面的理解就是，當知道  $\left(v_{0}, v_{1}, \ldots, v_{i-1}\right)$  遊走路徑後，遊走的下一個節點是  $v_{i}$  的概率是多少? 可是這裡的  $v_{i}$  是頂點本身沒法計算，於是引入一個映射函數$\Phi$，它的功能是將頂點映射成向量，轉化成向量後就可以對頂點  $v_{i}$  進行計算了。

　　　　$\Phi: v \in V \mapsto \mathbb{R}^{|V| \times d}$

　　但是怎麼計算這個概率呢？同樣借用詞向量中使用的skip-gram模型 

　　skip-gram模型有這樣3個特點:

• 不使用上下文 (context) 預測缺失詞 (missing word)，而使用缺失詞預測上下文。因為 $\left(\left(v_{0}\right),\left(v_{1}\right), \ldots,\left(v_{i}-1\right)\right)$  這部分太難算了，但是如果只計算一個 $\left(v_{k}\right)$ ， 其中 $v_{k}$  是缺 失詞，這就很好算。 和右邊 2 個窗口內的節點。
• 不考慮順序，只要是窗口中出現的詞都算進來，而不管它具體出現在窗口的哪個位置。

　　應用skip-gram模型後，優化目標變成了這樣：

　　　　$\underset{\Phi}{\operatorname{minimize}}  \quad-\log \operatorname{Pr}\left(\left\{v_{i-w}, \cdots, v_{i-1}, v_{i+1}, \cdots, v_{i+w}\right\} \mid \Phi\left(v_{i}\right)\right)$

九、Algorithm: DeepWalk

　　整個 DeepWalk 算法包含兩部分，一部分是隨機遊走的生成，另一部分是參數的更新。

　　算法：

　　第 3 行代表整個過程迭代次，每次為每個節點採樣一個隨機遊走。第 4 行代表對節點進行隨機排列，這不是必須的，但是可以加速隨機梯度下降的收斂。對於每個隨機遊走，使用第7行的 SkipGram 進行參數的更新。

十、SkipGram

　　SkipGram是一種語言模型，它最大化句子中大小的窗口內出現的詞的共現概率。算法2 展示了SkipGram在DeepWalk中的應用：

　　算法2 迭代出現在窗口 $w$（第1-2行）內的隨機遊走中的所有可能的組合。對於每個頂點，我們將每個頂點 $v_j$ 映射到它當前的表示向量$\Phi\left(v_{j}\right) \in \mathbb{R}^{d}$ (見圖3b)。給定 $v_j$ 的表示，我們希望最大限度地提高其鄰居在行走中的概率（第3行）。我們可以使用不同的分類器來學習這種後驗分佈。例如，使用邏輯回歸建模前面的問題將導致大量的標籤（約 $|V|$ ），可能是數百萬或數十億美元。這樣的模型需要大量的計算資源，可以跨越整個計算機集群。為了加快訓練時間，可以使用 Hierarchical Softmax 最大來近似概率分佈。

十一、Hierarchical Softmax

　　考慮到 $u_{k} \in V$，在第3行中計算 $\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)$ 是不可行的。計算配分函數（歸一化因子）成本昂貴。如果我們將 頂點 分配給二進制樹的葉子，預測問題就會變成樹中特定路徑的概率最大化(見 Figure 3c)。如果到頂點 $u_k$ 的路徑是由一系列樹節點識別的$\left(b_{0}, b_{1}, \ldots, b_{\lceil\log |V|\rceil}\right)$，$(b_0=root，b_{\lceil\log |V|\rceil}=u_{k})$，那麼

　　　　$\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)=\prod \limits _{l=1}^{\lceil\log |V|\rceil} \operatorname{Pr}\left(b_{l} \mid \Phi\left(v_{j}\right)\right)$

　　現在，$\operatorname{Pr}\left(b_{l} \mid \Phi\left(v_{j}\right)\right)$ 可以通過分配給節點 $b_l$ 的父節點的二進制分類器來建模。這降低了計算 $\operatorname{Pr}\left(u_{k} \mid \Phi\left(v_{j}\right)\right)$ 的計算複雜度，從 $O(|V|)$ 降低到 $O(log|V|)$ 。我們可以通過為隨機行走中的頻繁頂點分配更短的路徑來進一步加快訓練過程。霍夫曼編碼用於減少樹中頻繁元素的訪問時間。

十二、Parallelizability

　　如圖2所示，社交網絡隨機遊動中的頂點和一種語言中的單詞的頻率分佈都遵循冪律。這導致了罕見頂點的長尾，因此，影響Φ的更新本質上是稀疏的。這允許我們在多工作人員的情況下使用異步版本的隨機梯度下降(ASGD)的方法。鑒於我們的更新是稀疏的，並且我們沒有獲得一個鎖來訪問模型共享參數，ASGD將實現一個最佳的收斂速度[36]。雖然我們在一台機器上使用多個線程運行實驗，但已經證明了這種技術具有高度的可伸縮性，並且可以用於非常大規模的機器學習[8]。圖4顯示了並行化「深度行走」的效果。它顯示了隨着工作目錄的數量增加到8人，博客目錄和Flickr網絡的處理速度是一致的(圖4a)。它還表明，相對於連續運行的DeepWalk，預測性能沒有損失(圖4b)

　　上圖顯示了並行對DeepWalk的影響。圖(a)當多個任務同時進行時，算法的速度變快。圖(b)表明，並行運行下，DeepWalk的性能沒有受到影響。

• • SpectralClustering：該方法從圖 $G$ 的標準化拉普拉斯矩陣 $\widetilde{\mathcal{L}}$ 選擇 d-smallest 個特徵向量生成 $\mathbb{R}^d $ 的表示。利用$\widetilde{\mathcal{L}}$ 的特徵向量隱式地假設圖剪切將對分類有用。
  • Modularity：該方法從 $G$ 的  Modularity matrix B的  top-d 特徵向量生成 $\mathbb{R}^d $ 的表示。B 的特徵向量編碼了 $G$ 的模圖分區信息。使用它們作為特徵可以假設模塊化圖分區對分類很有用。
  • EdgeCluster：該方法使用 k-means 聚類對 $G$ 的鄰接矩陣進行聚類，它的性能與模塊化方法具有比較性，且擴展圖太大，無法進行譜分解。
  • wvRN：加權投票關係鄰居是一個關係分類器。給定頂點 $v_i$ 的鄰域 $\mathcal{N}_{i}$，wvRN 用其鄰域 ( 即 $\operatorname{Pr}\left(y_{i} \mid \mathcal{N}_{i}\right)=\frac{1}{Z} \sum \limits _{v_{j} \in \mathcal{N}_{i}} w_{i j} \operatorname{Pr}\left(y_{j} \mid \mathcal{N}_{j}\right)$ ) 估計 $\operatorname{Pr}\left(y_{i} \mid \mathcal{N}_{i}\right)$ 。它在真實網絡中顯示出驚人的良好性能，並被提倡作為一種合理的關係分類基線。
  • Majority：這種 naive 方法簡單地選擇訓練集中最頻繁的標籤。

十四、實驗

　　為了便於我們的方法與相關基線之間的比較，我們使用了與[39,40]中完全相同的數據集和實驗程序。具體來說，我們隨機抽取標記節點的一部分( $T_R$ )，並將它們作為訓練數據。其餘的節點被用作測試。我們重複這個過程 10 次，並報告了 $Macro-F1$ 和 $Micro-F1$ 的平均性能。如果可能的話，我們在這裡直接報告原始結果[39,40]。對於所有的模型，我們使用由 Lib Linear[10] 實現的  one-vs-rest 進行分類。我們給出了使用( $γ=80，w=10，d=128$ )行走的結果。（光譜聚類、模塊化、邊緣聚類）的結果使用了 Tang 和 Liu 的首選維數，$d=500$ 。

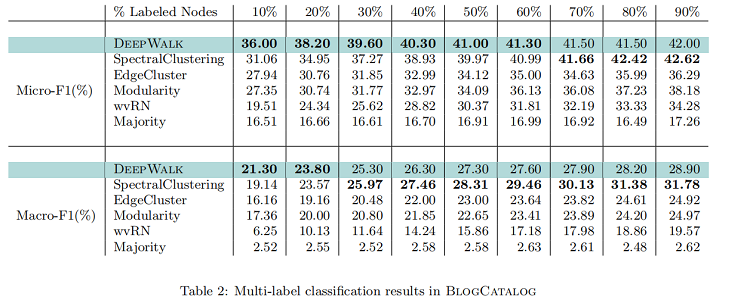
BlogCatalog

　　在本實驗中，我們將 BlogCatalog 網絡上的訓練比率( $T_R$ )從 10% 提高到 90% 。我們的結果如 Table 2 所示。粗體中的數字表示每一列中的最高性能。DeepWalk的性能始終優於 EdgeCluster 、Modularity 和 wvRN。事實上，當只使用 20% 的節點進行訓練時，DeepWalk 在獲得 90% 的數據時比這些方法表現得更好。SpectralClustering 的性能被證明更具競爭力，但當在 $Macro-F_1$ ($ T_R≤20% $) 和 $Micro-F1$(T_R≤60% )上的標記數據稀疏時，DeepWalk的性能仍然優於後者。當圖的一小部分被標記時，這種強大的性能是我們方法的核心優勢。在接下來的實驗中，我們研究了我們的表示在更稀疏標記的圖上的性能。

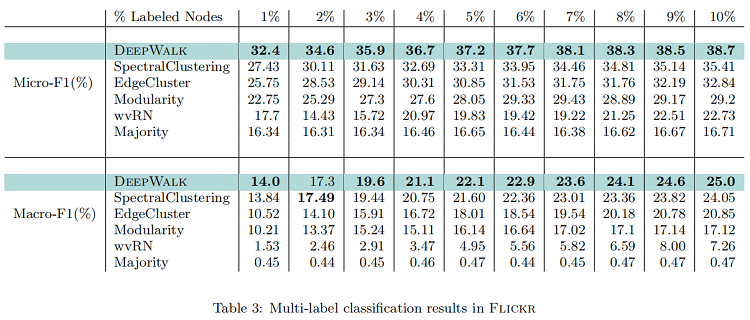
Flickr

　　在本實驗中，我們將 Flickr 網絡上的訓練比率( $T_R$ )從 $1%$ 變化到 $10%$。這相當於在整個網絡中有大約 800 到 8000 個節點被標記出來進行分類。Table 3 顯示了我們的結果，這與之前的實驗結果一致。與Micro-F1相比，DeepWalk 的性能比所有基線高出至少 $3%$。此外，當只有 $3%$ 的圖被標記時，它的 $Micro-F1$ 性能優於所有其他方法，即使它們得到了 $10%$ 的數據。換句話說，DeepWalk 可以比基線的訓練數據少 60%。它在 $Macro-F_1$ 中也表現得很好，最初表現接近BlogCatalog，但距離自己提高了 1%。

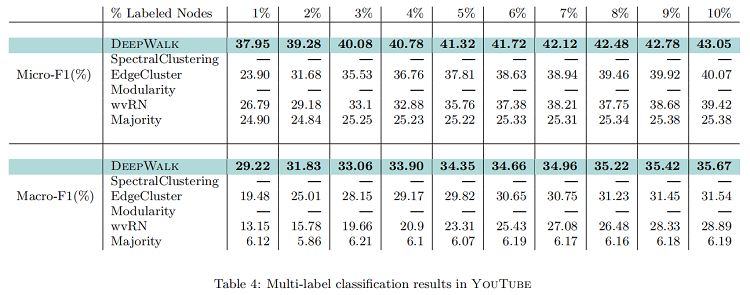
YouTube

　　YouTube 網絡比我們之前實驗過的要大得多，它的大小阻止了我們的兩種基線方法（SpectralClustering 和 Modularity ）在它上運行。它比我們之前考慮過的更接近一個真實世界的圖。訓練比例( $T_R$ ) 從 1% 到 10% 的結果如 Table 4 所示。他們表明，DeepWalk 在創建圖形表示方面顯著優於可伸縮的基線，即邊緣集群。當 1% 的標記節點用於測試時，$Micro-F1$ 提高了14%。$Macro-F1$ 顯示出相應的 10% 的增長。隨着訓練數據的增加，這一領先優勢逐漸縮小，但DeepWalk 以 $Micro-F1$ 領先 $3% $ 結束，$Macro-F1$ 提高了令人印象深刻的5%。這個實驗展示了性能的好處：可以通過使用社會表徵學習進行多標籤分類而發生。深度行走，可以縮放到大型圖形，並且在這樣一個稀疏標記的環境中表現得非常好。

Parameter Sensitivity

　　為了評估 DeepWalk 參數化的變化如何影響其在分類任務上的性能，我們在兩個多標籤分類任務( Flickr 和 BlogCatalog )上進行了實驗。在這個測試中，我們將窗口大小（Window size）和 行走長度（Walk Length） 固定為合理的值( $w=10，t=40$)，這應該強調局部結構。然後，我們改變潛在維度(d)的數量、每個頂點開始行走的次數（$γ$）和可用的訓練數據量( $T_R$ )，以確定它們對網絡分類性能的影響。

Effect of Dimensionality

　　Figure 5a顯示了增加我們的模型可用的潛在維度數的影響。

　　Figure 5a1 和 Figure 5a3 檢查了改變維數和訓練率的影響。Flickr和博客目錄之間的性能非常一致，並表明一個模型的最優維數取決於訓練示例的數量。(請注意，1%的 Flickr 擁有的標記例子大約與10%的博客目錄一樣多)。

　　Figure 5a2 和 Figure 5a3 檢查了改變每個頂點的維數和行走次數的影響。對於不同的 $\gamma $ 值，維度之間的相對性能相對穩定。這些圖表有兩個有趣的觀察結果。首先，大部分好處是通過在兩個圖中每個節點啟動 $\gamma =30$ 行走來實現的。第二，在這兩個圖中，不同的 $\gamma =30$ 值之間的相對差異是相當一致的。Flickr 比 BlogCatalog  多有一個數量級的邊，我們發現這種行為很有趣。

十五、結論

　　我們提出了 DeepWalk，一種學習頂點潛在社會表徵的新方法。利用截斷隨機遊動的局部信息作為輸入，我們的方法學習一種編碼結構規律的表示。在各種不同的圖上進行的實驗說明了我們的方法在具有挑戰性的多標籤分類任務上的有效性。

　　作為一種 online algorithm，DeepWalk也是可擴展的。我們的結果表明，我們可以為太大的無法運行光譜方法的圖創建有意義的表示。在如此大的圖上，我們的方法顯著優於其他設計來操作稀疏性的方法。我們還展示了我們的方法是可並行化的，允許工作人員同時更新模型的不同部分。

　　除了有效性和可擴展性外，我們的方法也是語言建模的一個有吸引力的泛化方法。這種聯繫是互惠互利的。語言建模的進步可能會繼續為網絡產生改進的潛在表示。在我們看來，語言建模實際上是從一個不可觀察到的語言圖中採樣的。我們相信，從建模可觀測圖中獲得的見解可能反過來會對建模不可觀測圖產生改進。

看完點個關注唄！！_{（總結不易）}