格的定義

偏序格

定義：給出一個偏序集（L,≤）,如果對於任意a,b∈L，L的子集{a, b}在L中都有一個最大下界(記為inf{a, b})和一個最小上界(記為sup{a, b}) 則稱（L，≤）為一個格。

🔔 全序集是一個格，不是所有偏序集都是格.

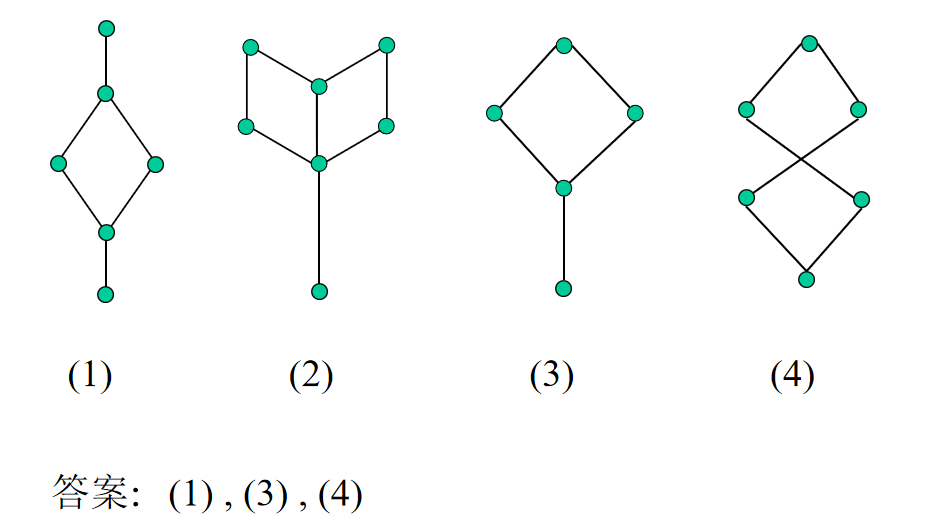
偏序子格

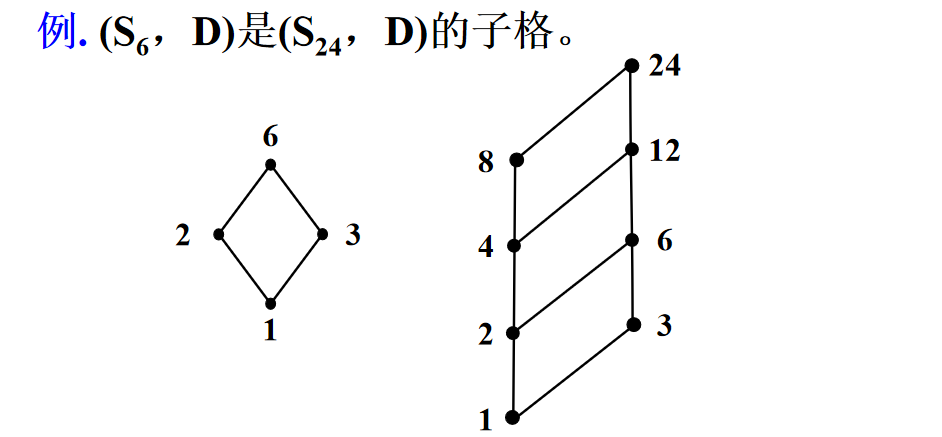
定義：設(L，≤)是格，S ⊆ L，如果(S，≤)是格，則稱(S，≤)是格(L，≤)的子格。

代數格

定義：設L是一個集合，×，⊕是L上兩個二元代數運算，如果這兩種運算對於L中元素滿足：

• 交換律：a×b=b×a，a⊕b=b⊕a。
• 結合律：a ×（b×c）=（a×b）× c，
  a ⊕（b⊕c）=（a⊕b）⊕ c。
• 吸收律：a ×（a⊕b）= a，
  a ⊕（a×b）= a。
  則稱此代數系統(L，×，⊕)為一個格。

🔔
1️⃣ 設(L, ×, ⊕)是格,則(L, ×)和(L, ⊕) 為交換半群

2️⃣ 滿足吸收律可推出它們一定滿足冪等律。

代數子格

設(L,×,⊕)是一個代數格，S ⊆ L，(S,×,⊕)稱為(L,×,⊕)的一個子格，當且僅當在運算×,⊕下，S是封閉的。

🔔 (S,×,⊕)是格(L,×,⊕)的子格的充要條件是: S ⊆ L 且（S,×,⊕）是一個格。

代數格與偏序格的等價性

定義：一個偏序格必是一個代數格；反之亦然.

代數子格與偏序子格的關係

• 若(S,×,⊕)是(L, ×, ⊕)的代數子格，則(S，≤）是 (L，≤)的偏序子格；

• 若(S，≤)是(L，≤)的偏序子格，則(S,×,⊕) 不一定是(L, ×, ⊕)的代數子格。 （因為代數子格必須滿足封閉性）

格的性質

格的其他性質

1️⃣ 設(L，≤)是一個格，a，b是 L 中任意元素，於是 a≤b <=> a×b = a <=> a ⊕ b = b

2️⃣ 設(L，≤)是一個格，a，b，c是 L 中任意元素，如果b≤c，則有 a×b ≤ a×c，a⊕b ≤ a⊕c

3️⃣ 設(L，≤)是一個格，a，b，c是L中任意元素。於是有分配不等式

• a⊕(b×c) ≤ (a⊕b)×(a⊕c)
• a×(b⊕c) ≥ (a×b)⊕(a×c)
  （記憶方法：最後進行 ⊕ 的式子小）
  🔔 在一般格中，分配律不是總成立的，但上述分配不等式總是成立的。

4️⃣ 設（L，≤）是一個格，a，b，c是 L 中任意元素，於是，a≤b <=> a⊕(b×c) ≤ b×(a⊕c)

格的同態和同構

1️⃣ 設(L,×,⊕)和(S,∧,∨)是兩個格，L到S內的映射g稱為(L,×,⊕)到(S,∧,∨)的格同態映射，如果對任意a，b∈L，都有

• g(a×b)= g(a)∧g(b)
• g(a⊕b) = g(a)∨g(b).

2️⃣ 格 L 到 L 內的同態映射稱為格的自同態映射

3️⃣ 若 g 是 L 到 S 上的同態映射，且是一對一的，則稱 g 是格同構映射，並稱格 L 與格 S 是同構的。
此時，對任意 x∈L，任意 y∈S ，有 g-1(g(x))=x，g(g-1(y))=y。

4️⃣ 格的同態映射一定是保序映射，但保序不一定是同態
設(L,×,⊕) ≡ (L, ≤)和(S,∧,∨) ≡ (S, ≤)是兩個格。如果 g 是 L 到 S 內的同態映射，則 g 是保序映射，
亦即，對任意 a，b∈L，若a≤b，則g(a)≤g(b)。

5️⃣ 設(L,×,⊕)是一個格，g 是此格的自同態映射，於是 g(L)是(L, ×, ⊕)的代數子格。

6️⃣ 設(L,×,⊕), (S,∧,∨)是兩個格，若 g 是 L 到 S 上的同構映射,則 g 的逆映射 g-1 是 S 到 L 上的同構映射。

7️⃣ 若格（L，×，⊕) ≡ (L, ≤)和格(S，∧，∨) ≡ (S, ≤) 同構 ，g 是其同構映射, 則對 L 中任意兩個元素a，b，有a≤b <=> g(a)≤g(b)

n 維格

幾種特殊的格

有界格

定義：格(L，≤)稱為有界格，如果它有一個最大元素(記為1)和一個最小元素(記為0)，亦即，對任意a∈L，都有 0≤a≤1, 0，1稱為格 (L，≤)的界。

🔔 有限格必是有界格，有界格不一定是有限格

1️⃣ 若(L,×,⊕, 0, 1)是有界格，則對任意a∈L，恆有
a ⊕ 0 = a， a × 1 = a，
a ⊕ 1 = 1， a × 0 = 0。

2️⃣ 余元素：在有界格(L，×，⊕，0，1)中，一個元素b∈L，稱為元素a∈L的余元素，如果a × b = 0， a ⊕ b = 1。

3️⃣ 在有界格中，一元素可能沒有餘元素；如果有餘元素，可以有一個或一個以上的余元素.

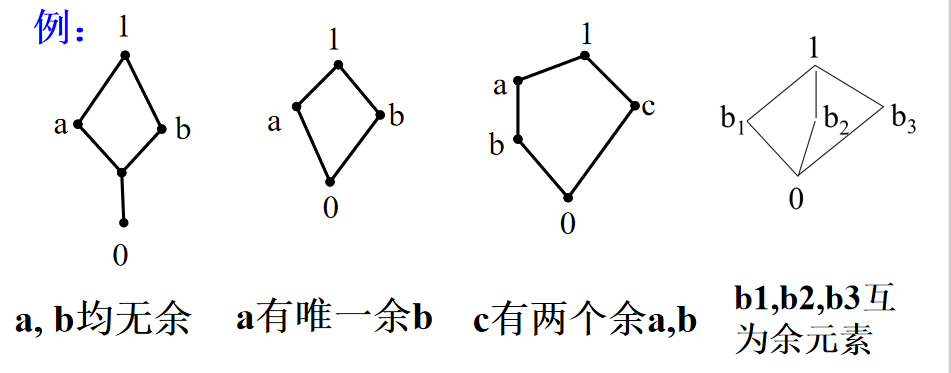
4️⃣ 在有界格（L,×,⊕, 0, 1)中，1是0的唯一 一個余元素，反之亦然。

有餘格

定義：稱有界格(L，×，⊕，0，1)是一個有餘格如果對 L 中每一個元素，都至少有一個余元素。

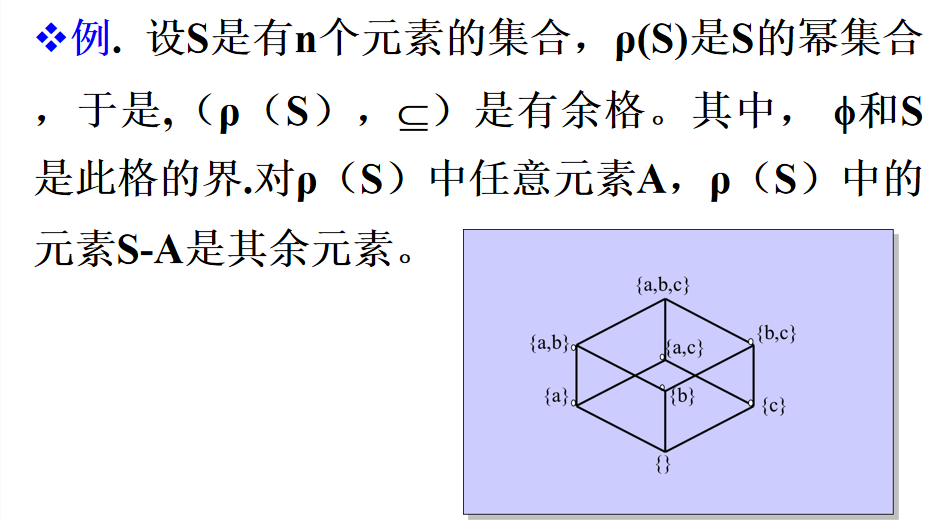
分配格

定義：格(L,×,⊕)稱為分配格，如果對任意 a，b，c∈L，恆有
a×(b⊕c) = (a×b)⊕(a×c)
a⊕(b×c) = (a⊕b)×(a⊕c)

🔔
1️⃣ 分配格定義中的兩個等式是等價的，可以互相推出

2️⃣ 但不是所有的格都是分配格

3️⃣ 分配格的任意子格仍是分配格。

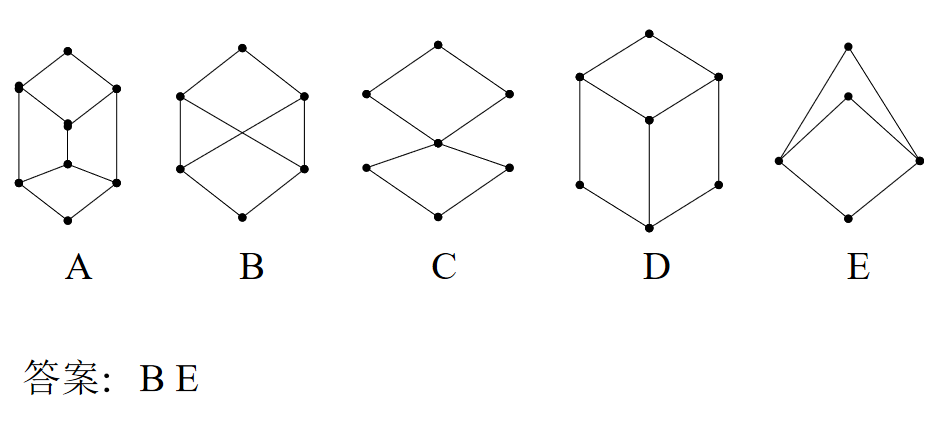
‼️ L是分配格當且僅當 L 既不含有與五角格同構的子格;也不含有與鑽石格同構的子格。

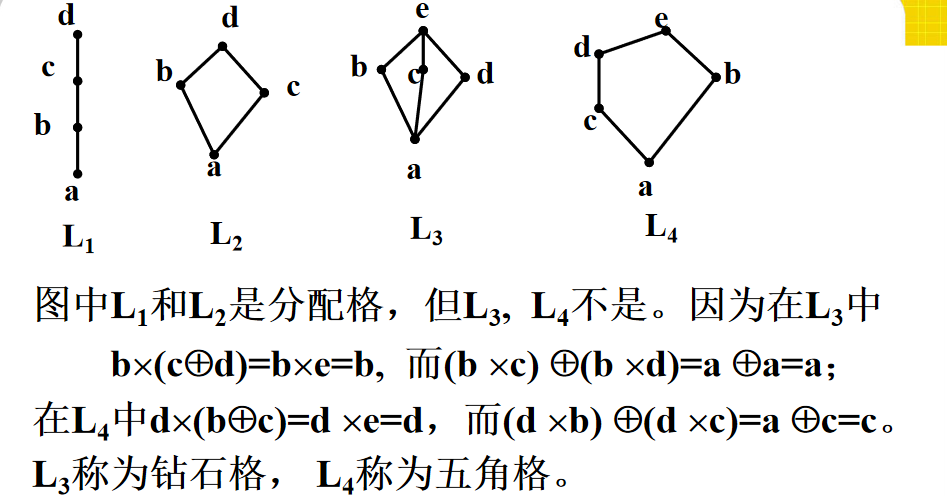
5️⃣ 任意一個鏈都是一個分配格

6️⃣ (德摩根定律) 設(L,×,⊕)是一個分配格，對任意a, b∈L，若a，b有餘元素a』, b』，則
(a×b)』= a』⊕b』 (a⊕b)』= a』×b』

7️⃣ 設格(L,×,⊕)是分配格，對任意a, b, c∈L，如果a×c = b×c，a⊕c = b⊕c，則a = b。

8️⃣ 設格(L,×,⊕)是一個有餘分配格（有界分配格），則對任意a∈L，a 的余元素 a′ 是唯一的。

模格

定義：設(L,≤)是一個格，對任意a, b, c∈L，如果a≤b，都有a⊕(b×c)= b×(a⊕c)則稱(L，≤)為模格。

🔔
1️⃣ 任意一個分配格都是模格

2️⃣ 模格不一定是分配格。

‼️

• 一個格 L 是模格當且僅當 L 不含與五角格同構的子格。
• 一個模格是分配格當且僅當 L 不含與鑽石格同構的子格
  

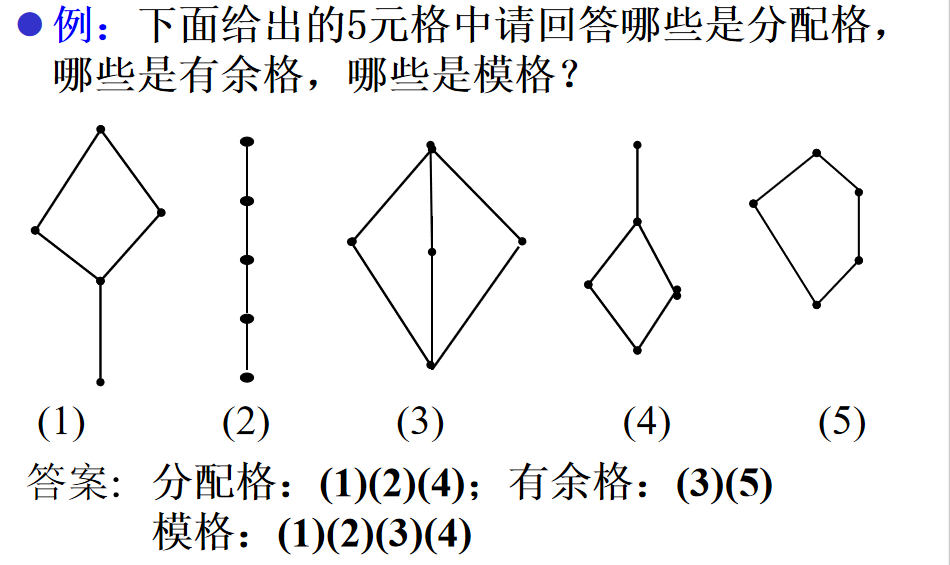
4️⃣ 格(L，≤)是模格的充要條件是：
對任意a，b，c∈L，如果a≤b，a×c=b×c，a⊕c=b⊕c，則必有a=b。

布爾代數

布爾代數的定義及其性質

定義： 一個有餘分配格是一個布爾代數。記為(B，·，+，ˉ，0，1)。

性質：

Huntington(亨廷頓)公理

定理: 設B是一個至少含有兩個不同元素的集合，·，+是定義在B上的兩種代數運算，如果對任意a，b，c∈B，滿足下面公理：

子代數

任給一個布爾代數 (B, ·, +, ¯, 0, 1)。若B的一個子集S包含0和1, 且(S，·，+，¯，0，1)仍是一個布爾代數,則稱S為B的子代數。

設（B，·，+，¯，0，1）是布爾代數.於是，B的子集S是B的子代數的充要條件是S在運算· ，+，¯ 下是封閉的。

往期回顧

離散數學（集合論）
離散數學（古典數理邏輯）
離散數學（圖與網絡）
離散數學（數論基礎）
離散數學（格與布爾代數）