徹底弄清楚前綴和與差分!
前綴和
一維前綴和
普通求和
同常我們對一維數組求和採用的是從頭到尾遍歷的方式,時間複雜度是O(n),但當計算很龐大的數據量時就很可能會超時!
int sum = 0;
for(int i = 0; i < nums.size(); i++)
sum += nums[i]
一維前綴求和
-
初始化前綴和數組(定義一個
s[i]數組,用來記錄(代表)前i項數據的和):s[i] = s[i - 1] + a[i]
註:
i是從1開始的,這樣就不用考慮邊界問題了。如:s[1] = s[0] + a[1],s[0] = 0 -
查詢操作:計算[l ~ r]的和:
s[r] - s[l - 1]。時間複雜度是O(1)

【acwing.795前綴和】
輸入一個長度為 n 的整數序列。
接下來再輸入 m 個詢問,每個詢問輸入一對 l,r。
對於每個詢問,輸出原序列中從第 ll 個數到第 rr 個數的和。
輸入格式
第一行包含兩個整數 n 和 m。
第二行包含 n 個整數,表示整數數列。
接下來 m 行,每行包含兩個整數 ll 和 rr,表示一個詢問的區間範圍。
輸出格式
共 m 行,每行輸出一個詢問的結果。
數據範圍
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤數列中元素的值≤1000輸入樣例:
5 3
2 1 3 6 4
1 2
1 3
2 4輸出樣例:
3
6
10
【參考代碼】
#include<iostream>
using namespace std;
int n,m;
const int N = 100000+10;
int a[N],s[N]; // 初始化數組了 a[0]、s[0]=0
int main()
{
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i];
//初始化前綴和數組s[i]
for(int i = 1; i <= n; i++) s[i] = s[i -1] + a[i];
int l, r;
while(m--)
{
cin>>l>>r;
//求[l~r]的和
cout<<s[r] - s[l - 1]<<endl;
}
return 0;
}
二維前綴和(子矩陣的和)
-
初始化前綴和數組(定義一個二維
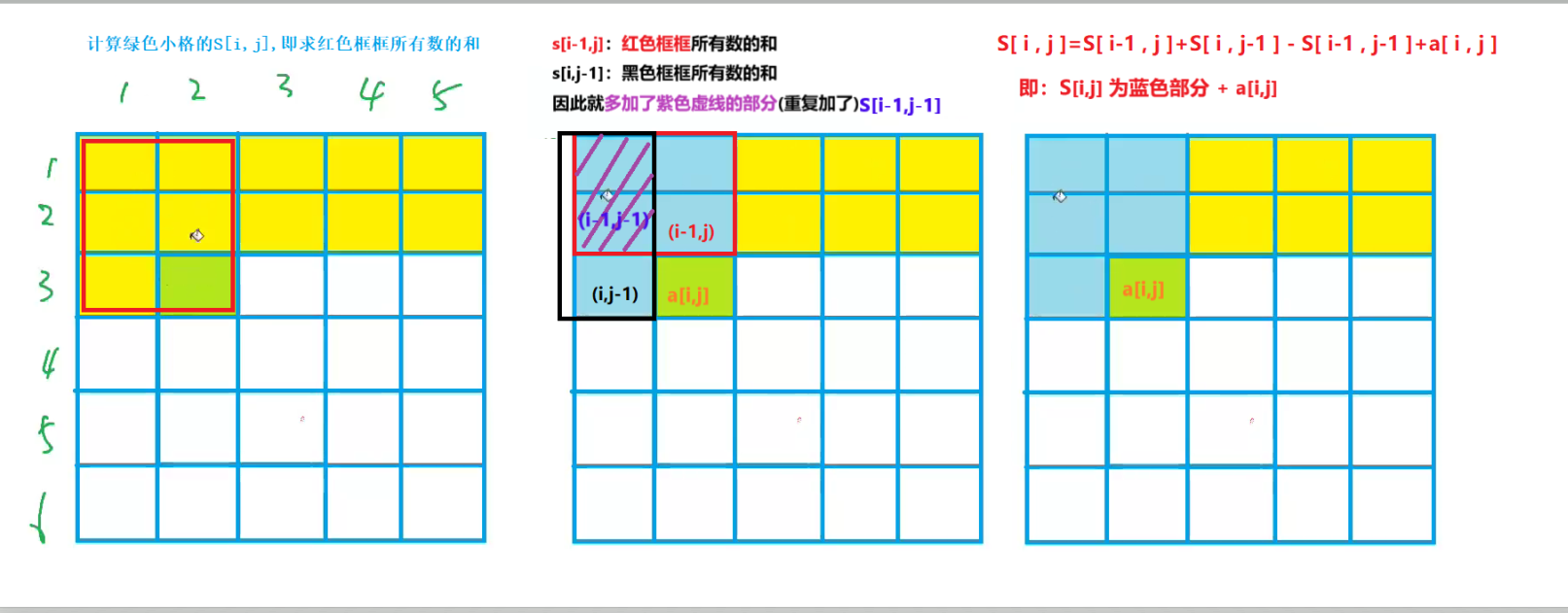
s[i][j]數組,用來記錄(代表)前(i,j)到原點所有數的和項數據的和)(1)S[i,j]是什麼:
S[i,j]即為圖中綠色部分所有數的的和為:
(2)S[i,j]怎麼計算:
S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]
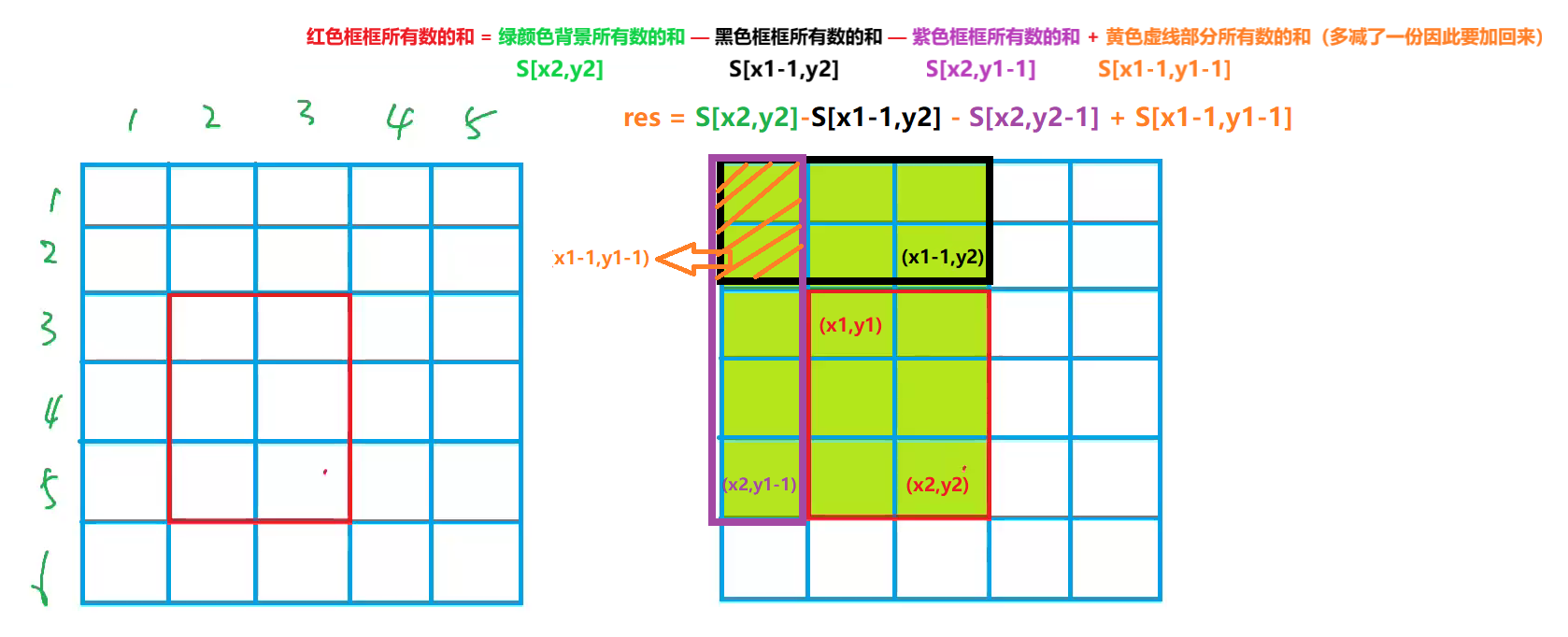
- (x1,y1),(x2,y2)這一子矩陣中所有數的和怎麼計算?
res = S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]
【acwing 796. 子矩陣的和】
輸入一個 n 行 m 列的整數矩陣,再輸入 q 個詢問,每個詢問包含四個整數 x1,y1,x2,y2表示一個子矩陣的左上角坐標和右下角坐標。
對於每個詢問輸出子矩陣中所有數的和。
輸入格式
第一行包含三個整數n,m,q。
接下來 n 行,每行包含 m 個整數,表示整數矩陣。
接下來 q 行,每行包含四個整數 x1,y1,x2,y2,表示一組詢問。
輸出格式
共 q 行,每行輸出一個詢問的結果。
數據範圍
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩陣內元素的值≤1000輸入樣例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4輸出樣例:
17
27
21
【參考代碼】
#include<iostream>
using namespace std;
const int N = 1000+10;
int a[N][N],s[N][N];
int main()
{
int n,m,q;
cin>>n>>m>>q;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
scanf("%d",&a[i][j]);
//1.初始化前綴和數組
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
while(q--)
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1 , &y1, &x2, &y2);
//2.計算(x1,y1)(x2,y2)子矩陣的和
int res = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
printf("%d\n",res);
}
return 0;
}
註:
同一維前綴和為了不額外考慮邊界問題我們從1開始對前綴和數組進行初始化。
當是大量數據的輸入輸出時
scanf和printf運行的是比cin和cout要快的!(所用時間更少)
差分
類似於數學中的求導和積分,差分可以看成前綴和的逆運算。
一維差分
差分數組:
首先給定一個原數組a:a[1], a[2], a[3],,,,a[n];
然後我們要構造一個數組b : b[1] ,b[2] , b[3],,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
a數組是b數組的前綴和數組,反過來我們把b數組叫做a數組的差分數組。即,每一個a[i]都是b數組中從頭開始到i的的一段區間和。
(1)如何構造差分b數組?
最為直接的方法
如下:
a[0 ]= 0;
b[1] = a[1] – a[0];
b[2] = a[2] – a[1];
b[3] =a [3] – a[2];
……..
b[n] = a[n] – a[n-1];
兩邊各自相加得:b[1] + b[2] + ,,, + b[n] = a[n]
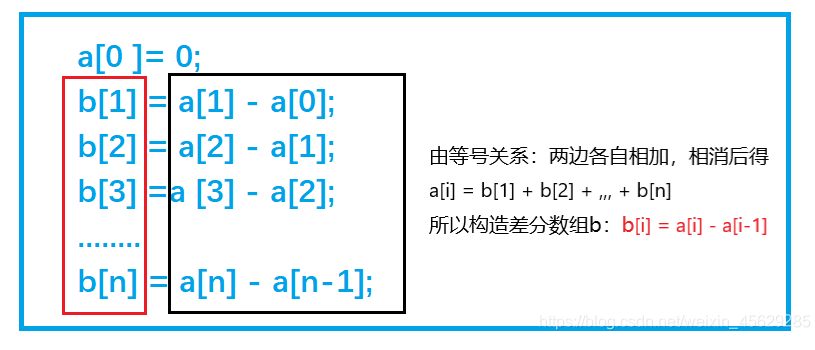
我們只要有b數組,最後通過前綴和運算,就可以在O(n) 的時間內得到a數組。
那我們構造出來的差分數組b到底有什麼用?,看下面的解釋你就了解啦!
(2)現在我們要給a數組在給定區間[l,r]上的每一個數加上c,即a[l] + c , a[l+1] + c , a[l+2] + c ,,,, a[r] + c。暴力的做法是for枚舉l~r,時間複雜度是O(n),如果我們需要對原數組執行m次這樣的操作,時間複雜度就會變成O(n*m)。當數據量很龐大時很可能就會超時,那有沒有更高效的方法呢?可以考慮一下差分操作!
始終要記得,a數組是b數組的前綴和數組對b數組的b[i]的修改,就一定會影響到a數組中從a[i]及往後的每一個數(圖示理解這句話!)

通過上面的解釋,那我們如何如和用差分數組b實現給a數組在[l,r]上+c呢?
-
首先讓差分b數組中的 b[l] + c ,a數組變成
a[l] + c ,a[l+1] + c,,,,,, a[n] + c;(通過上面的例子我們知道對b[l]進行了修改(+c),那麼從l及後面所有的數都受到了影響(+c)),但我們想要的是給a數組在定區間[l,r]上+c,即多了從r+1開始到後面所有數,這一段數據)。 -
為此,我們打個補丁,b[r+1] – c, a數組變成
a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;(即b[r+1] – c完成了減去上述從r+1開始都後面多出來的數據)
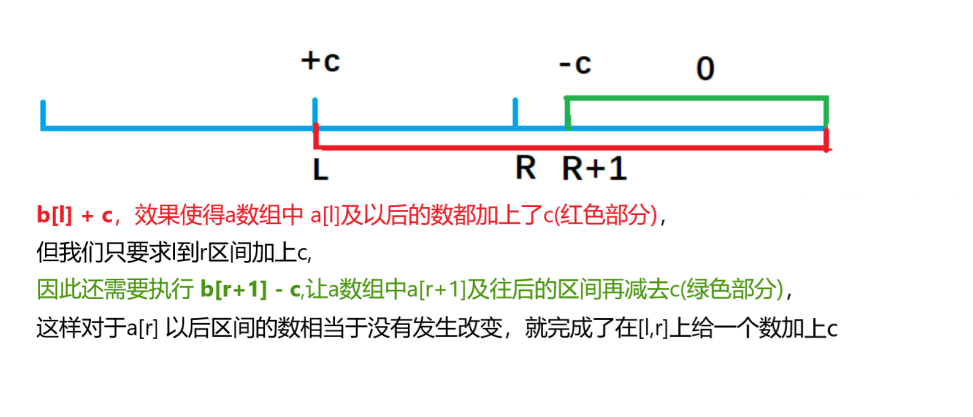
(3)如何求經過操作後的原數組a呢?
我們只要有了b數組,並對它進行b[l] += c,b[r + 1] -= c操作(使得a數組在[l,r]區間上每一個數+C),最後通過對b數組進行前綴和運算,就可以在O(n) 的時間內得到a數組。
【acwing 797 差分】
輸入一個長度為 n 的整數序列。
接下來輸入 m個操作,每個操作包含三個整數l,r,c,表示將序列中 [l,r][l,r] 之間的每個數加上 c。
請你輸出進行完所有操作後的序列。
輸入格式
第一行包含兩個整數 n 和 m。
第二行包含 n 個整數,表示整數序列。
接下來 m 行,每行包含三個整數l,r,c,表示一個操作。
輸出格式
共一行,包含 n 個整數,表示最終序列。
數據範圍
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整數序列中元素的值≤1000輸入樣例:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1輸出樣例:
3 4 5 3 4 2
【參考代碼】
#include<iostream>
using namespace std;
const int N = 100000+10;
int a[N],b[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
//構造差分數組
b[i] = a[i] - a[i - 1];
}
//給a數組[l,r]上每一個數加上c ===> b[l] += c, b[r+1] -= c
while(m--)
{
int l,r,c;
cin>>l>>r>>c;
b[l] +=c;
b[r + 1] -= c;
}
//求操作後的數組a———> 對b數組進行前綴和操作即可
for(int i = 1; i <= n; i++)
{
b[i] += b[i - 1];
printf("%d ",b[i]);
}
return 0;
}
【一維差分總結】
給區間[l,r]上的每一個數加上c:
b[l] += c,b[r + 1] -= c
二維差分
如果擴展到二維,我們需要讓二維數組被選中的子矩陣中的每個元素的值加上c,是否也可以達到O(1)的時間複雜度。答案是可以的,考慮二維差分。
a[][]數組是b[][]數組的前綴和數組,那麼b[][]是a[][]的差分數組
原數組: a[i][j]
我們去構造差分數組: b[i][j]
使得a數組中a[i][j]是b數組左上角(1,1)到右下角(i,j)所包圍矩形元素的和。
(1)如何構造b數組呢?
我們去逆向思考。
同一維差分,我們構造二維差分數組目的是為了 讓原二維數組a中所選中子矩陣中的每一個元素加上c的操作,可以由O(n*n)的時間複雜度優化成O(1)
在對子矩陣每一個數 + C操作之前,我們先要構造好差分數組b[i][j]
代碼如下:
// 構造差分數組
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];

(2)那我們如何給子矩陣(x1,y1),(x2,y2)中的每一個數都加上c呢?
已知原數組a中被選中的子矩陣為 以(x1,y1)為左上角,以(x2,y2)為右上角所圍成的矩形區域;
始終要記得,a數組是b數組的前綴和數組,比如對b數組的b[i][j]的修改,會影響到a數組中從a[i][j]及往後的每一個數。
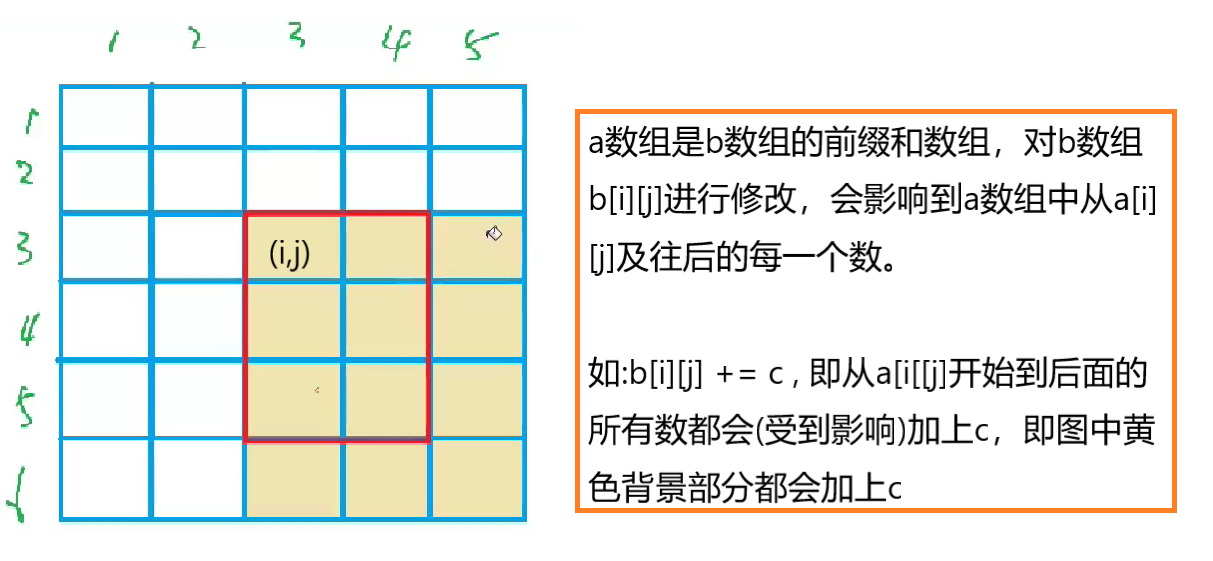
假定我們已經構造好了b數組,類比一維差分,我們執行以下操作
來使被選中的子矩陣中的每個元素的值加上c
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次對b數組執行以上操作,等價於:
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c;
我們畫個圖去理解一下這個過程:
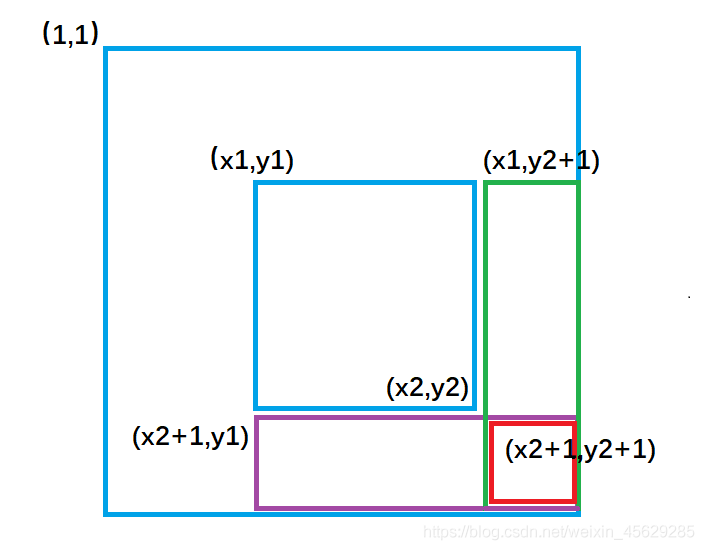
b[x1][ y1 ] +=c ; 對應圖1 ,讓整個a數組中藍色矩形面積的元素都加上了c。
b[x1,][y2+1]-=c ; 對應圖2 ,讓整個a數組中綠色矩形面積的元素再減去c,使其內元素不發生改變。
b[x2+1][y1]- =c ; 對應圖3 ,讓整個a數組中紫色矩形面積的元素再減去c,使其內元素不發生改變。
b[x2+1][y2+1]+=c; 對應圖4,,讓整個a數組中紅色矩形面積的元素再加上c,紅色內的相當於被減了兩次,再加上一次c,才能使其恢復。

我們將上述操作(子矩陣每一個數 + C)代碼如下。時間複雜度O(1):
{
//對a數組中的(x1,y1)到(x2,y2)之間的元素都加上了c
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
(3)如何求經過操作後的原數組a呢?
當我們構造了二維差分數組b[i][j],並對b[i][j]進行了 b[x1][y1]+=c; b[x2+1][y1]-=c; b[x1][y2+1]-=c; b[x2+1][y2+1]+=c;4個操作(使得a數組的子矩陣每一個數都加上了C),最後通過對b數組進行前綴和運算(二維前綴和運算),就可以在短時間時間內得到a數組。
【acwing 798. 差分矩陣】
輸入一個 n 行 m 列的整數矩陣,再輸入 q 個操作,每個操作包含五個整數 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一個子矩陣的左上角坐標和右下角坐標。
每個操作都要將選中的子矩陣中的每個元素的值加上 cc。
請你將進行完所有操作後的矩陣輸出。
輸入格式
第一行包含整數 n,m,q。
接下來 n 行,每行包含 m 個整數,表示整數矩陣。
接下來 q 行,每行包含 5 個整數 x1,y1,x2,y2,c,表示一個操作。
** 輸出格式**
共 n 行,每行 m 個整數,表示所有操作進行完畢後的最終矩陣。
數據範圍
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩陣內元素的值≤1000輸入樣例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1輸出樣例:
2 3 4 1
4 3 4 1
2 2 2 2
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
// 構造差分數組
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
while (q -- )
{
int x1, y1, x2, y2, c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
// 通過求差分數組b的前綴和來得到原數組a
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 前綴和公式
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
cout << endl;
}
return 0;
}
總結:
1.先構造好一維或者二維差分數組
2.差分的作用:是在O(1)時間內給某一段區間[l,r]或者子矩陣(x1,y1),(x2,y2)中的每一個數都加上C
註:如果文章有任何錯誤或不足,請各位大佬盡情指出,評論留言留下您寶貴的建議!如果這篇文章對你有些許幫助,希望可愛親切的您點個贊推薦一手,非常感謝啦





