二分查找法基本原理和實踐
概述
前面算法系列文章有寫過分治算法基本原理和實踐,對於分治算法主要是理解遞歸的過程。二分法是分治算法的一種,相比分治算法會簡單很多,因為少了遞歸的存在。
在計算機科學中,二分查找算法(英語:binary search algorithm),也稱折半搜索算法(英語:half-interval search algorithm)、對數搜索算法(英語:logarithmic search algorithm)[2],是一種在有序數組中查找某一特定元素的搜索算法。搜索過程從數組的中間元素開始,如果中間元素正好是要查找的元素,則搜索過程結束;如果某一特定元素大於或者小於中間元素,則在數組大於或小於中間元素的那一半中查找,而且跟開始一樣從中間元素開始比較。如果在某一步驟數組為空,則代表找不到。這種搜索算法每一次比較都使搜索範圍縮小一半。
二分查找算法在情況下的複雜度是對數時間。二分查找算法使用常數空間,無論對任何大小的輸入數據,算法使用的空間都是一樣的。除非輸入數據數量很少,否則二分查找算法比線性搜索更快,但數組必須事先被排序。儘管特定的、為了快速搜索而設計的數據結構更有效(比如哈希表),二分查找算法應用面更廣。
二分查找算法有許多中變種。比如分散層疊可以提升在多個數組中對同一個數值的搜索。分散層疊有效的解決了計算幾何學和其他領域的許多搜索問題。指數搜索將二分查找算法拓寬到無邊界的列表。二叉搜索樹和B樹數據結構就是基於二分查找算法的。
入門 demo
對二分法的概念了解後,下面來看一道示例:
153. 尋找旋轉排序數組中的最小值
已知一個長度為 n 的數組,預先按照升序排列,經由 1 到 n 次 旋轉 後,得到輸入數組。例如,原數組 nums = [0,1,2,4,5,6,7] 在變化後可能得到:
若旋轉 4 次,則可以得到 [4,5,6,7,0,1,2]
若旋轉 7 次,則可以得到 [0,1,2,4,5,6,7]
注意,數組 [a[0], a[1], a[2], …, a[n-1]] 旋轉一次 的結果為數組 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
給你一個元素值 互不相同 的數組 nums ,它原來是一個升序排列的數組,並按上述情形進行了多次旋轉。請你找出並返回數組中的最小元素 。
示例 1:
輸入:nums = [3,4,5,1,2]
輸出:1
解釋:原數組為 [1,2,3,4,5] ,旋轉 3 次得到輸入數組。
示例 2:
輸入:nums = [4,5,6,7,0,1,2]
輸出:0
解釋:原數組為 [0,1,2,4,5,6,7] ,旋轉 4 次得到輸入數組。
示例 3:
輸入:nums = [11,13,15,17]
輸出:11
解釋:原數組為 [11,13,15,17] ,旋轉 4 次得到輸入數組。
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整數 互不相同
nums 原來是一個升序排序的數組,並進行了 1 至 n 次旋轉
下面來看一下我寫的一個失敗版的答案,此時的我還沒入門二分法:
class Solution { public int findMin(int[] nums) { int left = 0; int right = nums.length-1; while (left<=right) { int middle = left + (right -left)/2; if (nums[middle] > nums[left]) { left = middle + 1; }else { right = right-1; } } return nums[left]; } }
輸入:[4,5,6,7,8,9,10,0,1,2,3]
輸出:10
結果:0
可以看到結果是不對,那這裡的問題是什麼呢?都說失敗是成功之母,我們只有分析清楚為啥我們的解法會存在問題,才能更好地明白二分法的精髓。
先從答案分析,這裡輸出 10,為啥會是 10。
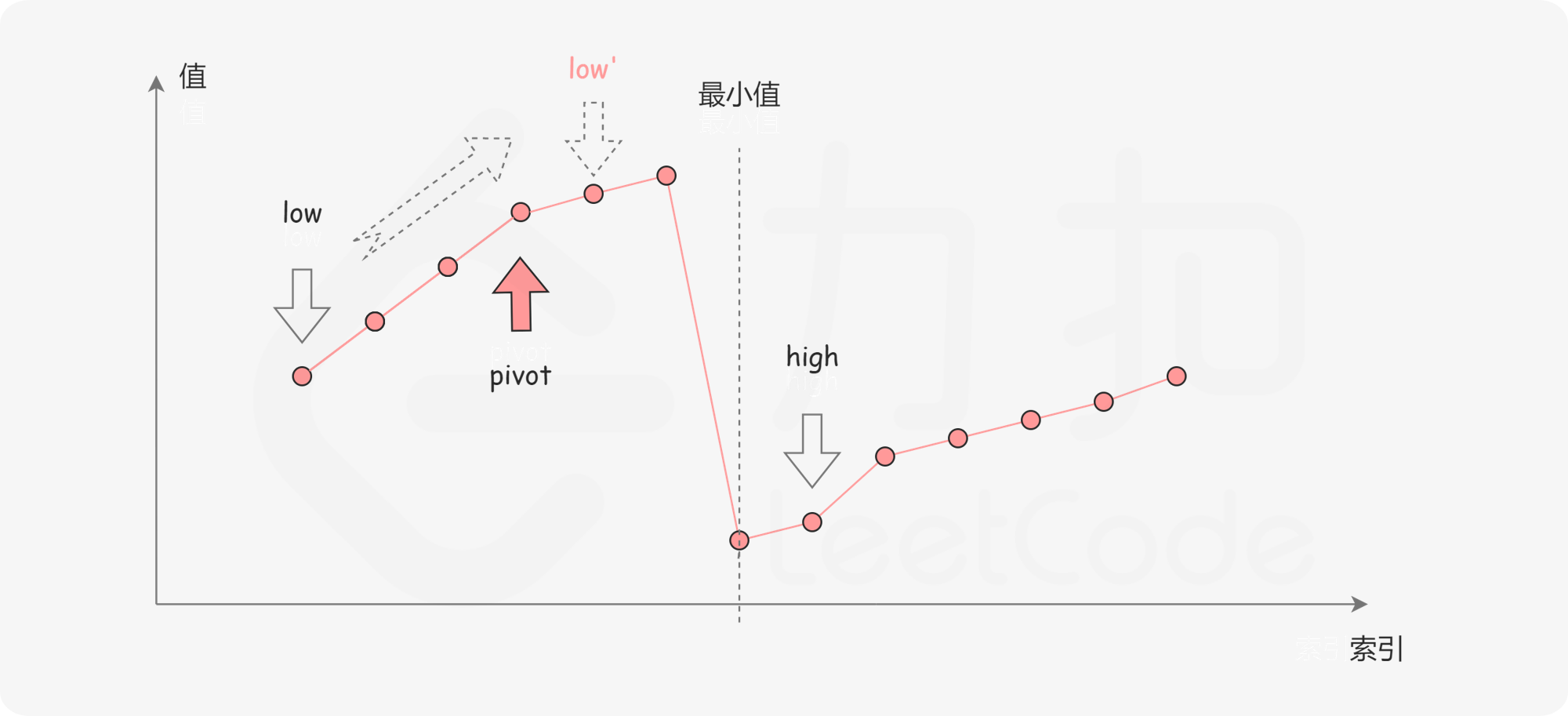
看上面這張圖,代碼邏輯寫的是 middle > left,那麼 left = middle +1; 這個邏輯這麼寫是沒有問題的。
接着看,當不滿足 middle > left,說明 middle 處於最小值的右半部分,這時候我們讓 right–。那如果 right 就是最小值呢,這時候就會錯過最小值。
還有如果 middle 是最大值呢?那麼 left= middle +1 就是最小值,此時你再去計算 middle ,就直接把最小值錯過了。比如輸入數組:[5,6,7,8,9,0,1,2,3,4];
還要考慮一種特殊情況,如果此時只有兩個元素了,有兩種情況 [1,2],[2,1] ,這時候如果按照 right–,就會直接取到第一個元素。所以在 middle 和 left 相等的時候也要在做額外的判斷。
完整版通過代碼如下:
class Solution { public int findMin(int[] nums) { int left = 0; int right = nums.length-1; while (left<right) { int middle = left + (right -left)/2; if (nums[middle] > nums[left] && nums[middle] > nums[right]) { left = middle +1;
// 說明最小值就在最右邊,此時處於只有兩個元素的時候 } else if(middle == left && nums[left] > nums[right]) { left = right; } else { right = right-1; } } return nums[left]; } }
當你看到這段代碼後,你懵逼了,這還是二分法嘛,分析下來這麼複雜。

那我們來看下官方給的代碼:
class Solution { public int findMin(int[] nums) { int low = 0; int high = nums.length - 1; while (low < high) { int pivot = low + (high - low) / 2;
// 最小值一定是在和 high 在一個區間內的,所以這裡要判斷 pivot 和 high 的大小關係,不能去判斷和 low 的關係 if (nums[pivot] < nums[high]) { high = pivot; } else { low = pivot + 1; } } return nums[low]; } }
是不是覺得官方代碼簡潔易懂。

那為啥這兩個解法的代碼會差這麼多,答案在於 middle 到底是應該和 left 比較,還是應該和 right 比較。
這也說明了方向的選擇的重要性。可是我們應該怎麼選擇呢。這個主要是在分析問題的時候要想清楚。個人覺得也可以這麼理解:
本題是找最小值的。從最小值到最右端,這其實就是單調遞增的,因此我們只要關注右半部分,拋棄左半部分就好。
那麼本題錯誤原因就是跟左邊進行比較,你再怎麼找,最後得出值都不在這一部分上,就導致你得添加很多額外的邏輯來確保可以找到值。
PS:對於二分法要時刻關注只有兩個元素的情況。這時候 middle = left。這時候注意 left 和 right 之間的關係。
通過這道題目相信大家已經對二分法有一定的認識了。
二分法思想
二分查找的思想就一個:逐漸縮小搜索區間。 如下圖所示,它像極了「雙指針」算法,left 和 right 向中間走,直到它們重合在一起:
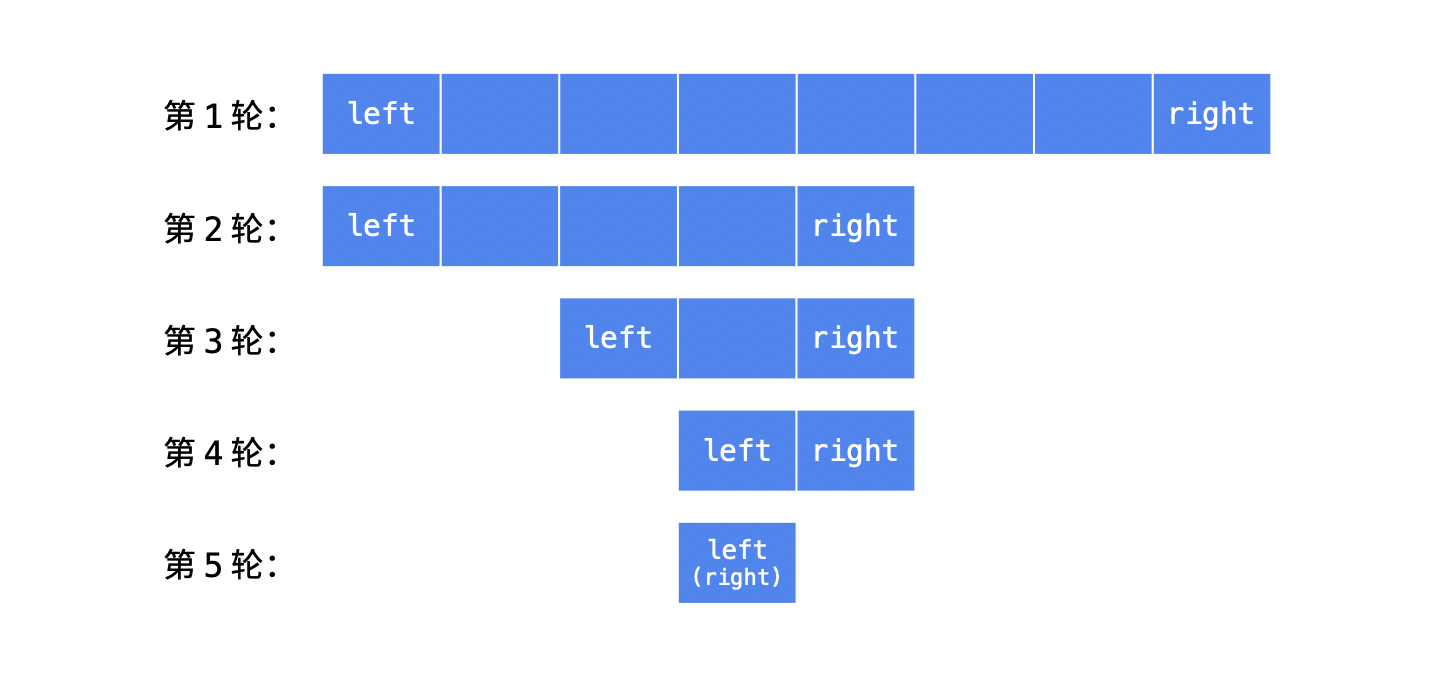
根據看到的中間位置的元素的值 nums[mid] 可以把待搜索區間分為三個部分:
![]()
- 情況 1:如果 nums[mid] = target,這時候我們直接返回即可。
- 情況 2: target 在 mid 左半部分 [left..mid – 1],此時分別設置 right = mid – 1 ;
- 情況 3: target 在 mid 右半部分 [mid+1..right],此時分別設置 left = mid + 1。
這樣就可以獲得二分法基本模板:
class Solution { public int search(int[] nums, int target) { int left = 0; int right = nums.length - 1; // 確保 left 和 right 都在數組可取範圍內 while (left <= right) { // < 還是 <= 按照自己的習慣即可 int mid = left + (right -left)/2; if (nums[mid] == target) { // 找到結果就返回 return mid; }else if(nums[mid] > target) { right = mid-1; } else { left = mid +1; } }
// 退出循環就說明沒找到 return -1; } }
雖然我們看到的寫法有很多,但思想就這一個;為什麼總是有朋友覺得二分難?因為有很多二分的寫法,雖然都對,但是對於新手朋友們來說有一定干擾,因為不同的寫法其實對應着不同的前提和應用場景,比起套用模板,審題、練習和思考更重要。「二分查找」就幾行代碼,完全不需要記憶,也不應該用記憶的方式解題.
下面解釋一些細節:
1、模板的結束條件是 left <= right ,也就是結果一定是在 while 裏面找到的。否則就是沒找到。
2、有些學習資料上說 while (left < right) 表示區間是 [left..rihgt) ,為什麼你這裡是 [left..rihgt]?
區間的右端點到底是開還是閉,完全由編寫代碼的人決定,不需要固定。主要還是看你 left 和 right 的取值。 如果 right = nums.length ; 那麼其實 right 這個位置是取不到的,也就是開區間了。所以開閉就是看點位能不能取到。
3、有些學習資料給出了三種模板,例如「力扣」推出的 LeetBook 之 「二分查找專題」,應該如何看待它們?
回答:三種模板其實區別僅在於退出循環的時候,區間 [left..right] 里有幾個數。
-
while (left <= right) :退出循環的時候,right 在左,left 在右,區間為空區間,所以要討論返回 left 和 right;
-
while (left < right) :退出循環的時候,left 與 right 重合,區間里只有一個元素,這一點是我們很喜歡的;
-
while (left + 1 < right) :退出循環的時候,left 在左,right 在右,區間里有 2 個元素,需要編寫專門的邏輯。這種寫法在設置 left 和 right 的時候不需要加 1 和減 1。
看似簡化了思考的難度,但實際上屏蔽了我們應該且完全可以分析清楚的細節。退出循環以後一定要討論返回哪一個,也增加了編碼的難度。
我個人的經驗是:
-
while (left <= right) 用在要找的數的性質簡單的時候,把區間分成三個部分,在循環體內就可以返回;
-
while (left < right) 用在要找的數的性質複雜的時候,把區間分成兩個部分,在退出循環以後才可以返回;
-
完全不用 while (left + 1 < right) ,理由是不會使得問題變得更簡單,反而很累贅。
很多題目在二分法的基礎上有變化,我們要學會靈活變化。還要理解題意。
示例:
給定一個排序數組和一個目標值,在數組中找到目標值,並返回其索引。如果目標值不存在於數組中,返回它將會被按順序插入的位置。
請必須使用時間複雜度為 O(log n) 的算法。
示例 1:
輸入: nums = [1,3,5,6], target = 5 輸出: 2
示例 2:
輸入: nums = [1,3,5,6], target = 2 輸出: 1
示例 3:
輸入: nums = [1,3,5,6], target = 7 輸出: 4
示例 4:
輸入: nums = [1,3,5,6], target = 0 輸出: 0
示例 5:
輸入: nums = [1], target = 0 輸出: 0
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums為無重複元素的升序排列數組-104 <= target <= 104
class Solution { public int searchInsert(int[] nums, int target) { int left =0; int right = nums.length -1; while (left<=right) { int mid = left + (right-left)/2; if (nums[mid] == target) { return mid; } if (nums[mid]>target) { right = mid-1; }else { left = mid+1; } } // 沒找到,那麼 left 就是它所處的位置 return left; } }
注意一點:二分法只是用於有序數組,如果是無序的,此時是無法確定邊界的,這時候我們就需要自己創造條件,找到數組的有序部分。
比如下面兩道,大家可以自己找二分法題目去練習。
33. 搜索旋轉排序數組
81. 搜索旋轉排序數組 II
關於二分法的理論就講到這裡了,剩下的就是靠大家多多練習了。
算法系列文章:
參考文章
//leetcode-cn.com/problems/search-insert-position/solution/te-bie-hao-yong-de-er-fen-cha-fa-fa-mo-ban-python-/